1 Introduction

A non-decreasing and right-continuous bivariate function \(C:[0,1]\times [0,1]\rightarrow [0,1]\) is called a copula if it satisfies following conditions:

  • \(C(s,0)=C(0,s)=0\) and \(C(s,1)=C(1,s)=s\), \(\forall s\in [0,1]\),

  • \(\forall \left( {s_1 ,s_2 ,t_1 ,t_2 } \right) \in [0,1]^{4},\) such that \(s_1 \le s_2 \) and \(t_1 \le t_2 \),

    $$\begin{aligned} C(s_2 ,t_2 )-C(s_2 ,t_1 )-C(s_1 ,t_2 )+C(s_1 ,t_1 )\ge 0. \end{aligned}$$
    (1.1)

    Eventually, for twice differentiable, 2-increasing property (1.1) can be replaced by the condition

    $$\begin{aligned} c(s,t)={\partial ^{2}C(s,t)}/{\partial s\partial t\ge 0}, \end{aligned}$$
    (1.2)

    where c(s, t) is the so-called copula density.

Firstly, let us recall that the random variables X and Y are exchangeable, if (X, Y) and (Y, X) are identically distributed. Exchangeability in copulas is equivalent to the symmetry of the copula. In other words, a copula C is symmetric if \(C(s,t)=C(t,s)\), for every \((s,t)\in [0,1]^{2}\), otherwise C is asymmetric. Second, the random variables X and Y are Positively Quadrant Dependent (PQD) if \(P\left( {X\le x,Y\le y} \right) \ge P\left( {X\le x} \right) P\left( {Y\le y} \right) \), for every \((x,y)\in \mathfrak {R}^{2}\) or equivalently \(C(s,t)\ge st\), for every \((s,t)\in [0,1]^{2}\). Let \(C_1 \) and \(C_2 \) be two copulas, the copula \(C_2 \) is said to be more concordant (or more PQD) than the copula \(C_1 \), (shortly \(C_1 <C_2 )\), if \(C_1 (s,t)<C_2 (s,t)\), for every \((s,t)\in [0,1]^{2}\).

The study of copulas and their application has been developed a lot in the past decades, as a tool to describe the dependence of random variable (see e.g. surveys by [12, 17, 21]). However, copulas play a very important role in Mathematical Modeling and Simulation. So it is very meaningful to construct different kinds of copulas. One of the most popular parametric families of copulas, which were studied by [11, 13, 22], is the Farlie–Gumbel–Morgenstern (FGM) copula defined by

$$\begin{aligned} C^{FGM}(s,t)=st\left[ {1+\theta \left( {1-s)(1- t} \right) } \right] , \theta \in [-1 , 1], \forall (s,t)\in [0,1]^{2}, \end{aligned}$$
(1.3)

where \(\theta \) is called the association parameter. The FGM copula is PQD, for \(\theta \in (0, 1]\). However, this copula has been shown to be somewhat limited. This limitation for the dependence parameter \(\theta \in [-1, 1]\), the Spearman’s rho and Kendall’s tau, are \(\rho _S =\theta /3\in [-1/3, 1/3]\) and \(\tau _k =2\theta /9\in [-2/9, 2/9]\), respectively.

Since the correlation domain of FGM copula is limited, more general copulas have been introduced with the aim of improving the correlation range. An alternative approach to generalize the FGM copula was the symmetric semi-parametric extension that is defined by [26]. It was extensively studied in ([3] and [2]). [15] developed Polynomial-type single-parameter extensions of FGM copula. They showed that \(\rho _S\) can be increased up to approximately 0.375 while the lower bound remains −0.33. [19] set conditions for positive quadrant dependence and studied a class of bivariate uniform distribution with positive quadrant dependence property by generalizing the uniform representation of a well-known FGM copula. By a simple transformation, they also obtained families of bivariate distributions with pre-specified marginals. [4] further extended the family introdueced by [15] to the associated Spearman’s \(\rho _S \in [-0.48, 0.5016]\). [25] and [1] proposed a new class of bivariate copulas dependent on two univariate functions which generalizes known families of copulas such as FGMcopula family. [5] proposed a new class of generalized FGM copula and showed that their generalization can improve the correlation domain of FGM copula. Recently, ([23, 24]) further extended the family given by [5]. Their studied FGM copulas have range of Spearman’s \(\rho _S \in [-0.48 , 0.5308]\), which is wider than that of the other FGM families of copulas discussed in literature.

In this regard, this paper proposes another generalized class of FGM copula, which includes some extended copulas introduced in recent years, and can improve the correlation range i.e. the proposed family covers some of the introduced family in the literature and its correlation range is more efficient. From another perspective, this presented family, is an extension of the generalized FGM copula discussed in [5]. The main contribution of this paper includes the followings: first, an extension of FGM copula and some interesting properties are presented. Second, properties and the general formulas for association measures of this family is its capability. The main feature of this family is capability for modeling a wider range of dependence. This permits us to extend the range of potential applications of the family in various branches of sciences.

The rest of the paper is as follows: the new extension and their basic characteristics are described in Sect. 2. Section 3 is dedicated to a remark and a property of the new class. Some general formulas for well-known association measures of this class are obtained in Sect. 4. Section 5 is devoted to the application and simulation results.

2 A new class of bivariate FGM copula and basic properties

To consider the continuous function \(\psi :[0,1]\times [0,1]\rightarrow [0,1]\) with additional properties:

  • \(\psi \) is continuously differentiable on (0, 1),

  • \(s\psi _s \left( {s,t} \right) \rightarrow 0,\) as

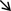
    figure a

    0,

  • \(st\psi _{st} \left( {s,t} \right) \rightarrow 0 ,\) as (s, t)

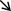
    figure b

    (0, 0),

  • \(s\psi _s \left( {s,t} \right) \) converges as

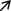
    figure c

    1,

  • \(st\psi _{st} \left( {s,t} \right) \) converges as (s, t)

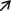
    figure d

    (1, 1),

where \(\psi _s \left( {s,t} \right) ={\partial \psi \left( {s,t} \right) }/{\partial s} , \psi _t \left( {s,t} \right) ={\partial \psi \left( {s,t} \right) }/{\partial t} \) and \(\psi _{st} (s,t)={\partial ^{2}\psi \left( {s,t} \right) }/{\partial s\partial t} \).

As an example, the function \(\psi (s,t)=(1-s^{\alpha }) t (1-st)(1-t),0<\alpha \le 1\), for all \((s,t)\in [0,1]^{2}\) is satisfied in the above conditions.

Definition 2.1

Based on the function \(\psi \) and its properties, suppose that the strictly continuous function \(\psi :[0,1]\times [0,1]\rightarrow [0,1]\) is differentiable on (0, 1). A function \(C_\theta ^{\psi ,p}\) on \([0,1]\times [0,1]\) is defined as

$$\begin{aligned} C_\theta ^{\psi ,p} (s,t)=st [1+\theta \psi (s,t)]^{p}, \quad p\in [1,\infty )\, \mathrm{and}\, \forall (s,t)\in [0,1]^{2}, \end{aligned}$$
(2.1)

for \(\theta \in \Theta \subseteq [-1 , 1]\).

The concrete amount of the parameter space \(\Theta \) is dependent on the properties of the function \(\psi \). We assume that \(\psi \) do not change their sign on [0, 1] in order to obtain unique determined dependence structure. Note that the copula is limited to the range of [0, 1] and therefore, \( [1+\theta \psi (s,t)]^{p}\) should be bounded on [0, 1]. The following theorem gives sufficient and necessary conditions on \(\psi \) to ensure that \(C_\theta ^{\psi ,p}\) is a bivariate copula.

Theorem 2.1

Let \(\psi \) be differentiable, non-negative and monotonically decreasing or non-positive and monotonically increasing on [0, 1]. If

  1. A1.

    \(\psi \left( {x,1} \right) =\psi \left( {1,x} \right) =0\), \(\forall x\in [0,1]\),

  2. A2.
    1. (i)

      If \({\psi }^{\prime }_x \), for every \(x\in [0,1]\) and \({\psi }^{\prime }_{st}\) have the same sign for every \((s,t)\in [0,1]^{2}\), then \(C_\theta ^{\psi ,p} \) is a copula for \(\theta \in [0,1]\); i.e. \(\Theta = [0,1]\).

    2. (ii)

      If \({\psi }^{\prime }_x \), for every \(x\in [0,1]\) and \({\psi }^{\prime }_{st} \) do nothave the same sign for every \((s,t)\in [0,1]^{2}\), then \(C_\theta ^{\psi ,p} \) is a copula for every \(\theta \in [-1,0]\); i.e. \(\Theta = [-1,0]\).

Proof

The proof involves two steps:

First, it is clear that \(C_\theta ^{\psi ,p} (x,1)=C_\theta ^{\psi ,p} (1,x)=x\), \(\forall x\in [0,1] \Leftrightarrow \)(A1).

Second,

(i) Since \({\psi }^{\prime }_x \) and \({\psi }^{\prime }_{st} \) are differentiable and monotone on [0, 1] and have the same sign, eventually for twice differentiable \(C_\theta ^{\psi ,p} \) the 2-increasing property (1.2) can be replaced by the condition

$$\begin{aligned} c_{\theta }^{{\psi ,p}} (s,t)= & {} \partial ^{2} C_{\theta }^{{\psi ,p}} (s,t)/\partial s\partial t\nonumber \\= & {} [1 + \theta \psi (s,t)]^{{p - 2}} \big \{ \big ( {1 + \theta \psi (s,t)} \big )^{2}+ st{} p(p - 1)\theta ^{2} \psi _{t} (s,t)\psi _{s} (s,t)\nonumber \\&{ + p\theta \big ( {1 + \theta \psi (s,t)} \big )\big ( {t\psi _{t} (s,t) + s\psi _{s} (s,t) + st\psi _{{st}} (s,t)} \big )} \big \} \end{aligned}$$
(2.2)

is nonnegative, if \({\psi }^{\prime }_x \) and \({\psi }^{\prime }_{st} \) have the same sign, and \(\theta \in [0 , 1]\). Because, let\(\theta \in [0 , 1]\), then

$$\begin{aligned} \psi _t (s,t) \psi _s (s,t)\ge 0, \quad \forall s,t\in [0,1] \end{aligned}$$

and

$$\begin{aligned} t\psi _t (s,t)+s\psi _s (s,t)+st\,\psi _{st} (s,t)\ge 0, \quad \forall s,t\in [0,1] \end{aligned}$$

with \(\psi :[0,1]\times [0,1]\rightarrow [0,1]\). Therefore,

$$\begin{aligned} \begin{array}{l} \left( {1+\theta \psi (s,t)} \right) ^{2}+s t p (p-1) \theta ^{2}\psi _t (s,t) \psi _s (s,t) \\ +p\theta \left( {1+\theta \psi (s,t)} \right) \left( {t\psi _t (s,t)+s\psi _s (s,t)+st\psi _{st} (s,t)} \right) \ge 0 \\ \end{array}, \quad \forall s,t\in [0,1]. \end{aligned}$$

(ii) If \(\theta \in [-1 , 0]\) and \({\psi }^{\prime }_x \) and \({\psi }^{\prime }_{st} \) do not have the same sign. Then, similar to (i), we have

$$\begin{aligned} \psi _t (s,t)\psi _s (s,t)\ge 0, \quad \forall s,t\in [0,1] \end{aligned}$$

and

$$\begin{aligned} \theta \left( {t\psi _t (s,t)+s\psi _s (s,t)+st\psi _{st} (s,t)} \right) \ge 0, \quad \forall s,t\in [0,1] \end{aligned}$$

with \(\psi :[0,1]\times [0,1]\rightarrow [0,1]\).

So, the function \(C_\theta ^{\psi ,p} \) satisfies 2-increasing property. \(\square \)

Corollary 2.1

Let \(\psi :[0,1]\times [0,1]\rightarrow [0,1]\) be differentiable and monotonic on [0, 1], fulfilling the conditions

  1. B1.

    \(\psi \left( {x,1} \right) =\psi \left( {1,x} \right) =0\), \(\forall x\in [0,1]\),

  2. B2.

    \(\left| {s{\psi }^{\prime }_s (s,t)} \right| \le 1\),\(\left| {t{\psi }^{\prime }_t (s,t)} \right| \le 1\), and \(\left| {st{\psi }^{\prime }_{st} (s,t)} \right| \le 1\),\(\forall s,t\in [0,1]\).

Then, the function \(C_\theta ^{\psi ,p} \) is a bivariate copula for \(\theta \in [-1,1]\); i.e. \(\Theta = [-1,1]\).

Proof

Similar to Theorem 1, with added condition (B2).

As an example, the function \(\psi (s,t)=(1-s^{\alpha })(1-t^{\alpha })\), for every \(\alpha \ge 0\) and the admissible range of parameter \(\theta \in \left[ {-\left( {\max \{1,p\}} \right) ^{-1} , p^{-1}} \right] \), the family \(C_\theta ^{\psi ,p} \) reduce to the extended FGM copula introduced by [5].

Note that \(\theta \) is the parameter that shows dependence structure of the family \(C_\theta ^{\psi ,p} \) so that \(\theta =0\) or \(p=0\), leads to the independence of S and T. By Theorem 2.1, the concreted amount of the parameter space \(\theta \) depends on the properties of the function \(\psi \) that has been investigated via (2.2) for every s and t in [0, 1]. The class \(C_\theta ^{\psi ,p}\) is PQD if and only if \(1+\theta \psi (s,t)\ge 0\), for all s and t in [0, 1], that implies the family \(C_\theta ^{\psi ,p} \) is more concordant (or more PQD) than the family \(C_\theta ^{\psi ,1} \), written \(C_\theta ^{\psi ,1} (s,t)<C_\theta ^{\psi ,p} (s,t)\) for every s and t in [0, 1]. It can introduce new sub-families of family (2.1) by several generalizations of \(\psi \).If \(\psi (s,t)=\psi (t,s)\), for every s and t in [0, 1], then the family ‘\(C_\theta ^{\psi ,p}\) is symmetric, otherwise is asymmetric. As an example, let \(\psi (s,t)=1-\sqrt{1-(1-s^{a})(1-t^{a})},a\ge 1\), then the generated copula is a symmetric copula. Also, let \(\psi (s,t)=(1-\sqrt{s^{a}})(1-t),a\ge 1\), then the generated copula is an asymmetric copula. In particular cases, let \(\psi (s,t)=f(s)f(t)\), where \(f:[0,1]\rightarrow [0,1]\) is a continuous differentiable function on (0, 1), and \(f (1)=0\), then by Theorem 2.1, the generated family is a symmetric bivariate copula. Moreover, let \(\psi (s,t)=f_1 (s)f_2 (t)\), where \(f_1 , f_2 :[0,1]\rightarrow [0,1]\), are continuous differentiable functions on (0, 1) and \(f_1 (1)=f_2 (1)=0\), then by Theorem 2.1, the generated family is an asymmetric bivariate copula ([7]). \(\square \)

3 Some known copulas and one property

In this section, we present a remark and a property of the family \(C_\theta ^{\psi ,p} \) introduced in (2.1).

Remark 3.1

The family \(C_\theta ^{\psi ,p} \) includes some known family of FGM copulas introduced by researchers in recent years, which are as follows:

  1. (i)

    If \(\psi (s,t)=(1-s)(1-t), \forall s,t\in [0,1]\), and \(p=1\), the family \(C_\theta ^{\psi ,p}\) reduce to the symmetric FGM copula discussed by [11, 13, 22].

  2. (ii)

    If \(\psi (s,t)=(1-s^{\alpha })(1-t^{\alpha }),\forall s,t\in [0,1], \alpha \ge 0\), and \(p=1\), the family \(C_\theta ^{\psi ,p} \) reduce to the symmetric extended FGM copula introduced by [15].

  3. (iii)

    If \(\psi (s,t)=s^{q}(1-s)^{q}t^{q}(1-t)^{q},\forall s,t\in [0,1],q\ge 1\), and \(p=1\), the family \(C_\theta ^{\psi ,p} \) reduce to the symmetric extended FGM copula introduced by [19].

  4. (iv)

    If \(\psi (s,t)=(1-s^{\gamma })^{\lambda }(1-t^{\gamma })^{\lambda },\forall s,t\in [0,1], \gamma \ge 0,\lambda \ge 1\), and \(p=1\), the family \(C_\theta ^{\psi ,p} \) reduce to the symmetric extended FGM copula introduced by [4].

  5. (v)

    If \(\psi (s,t)=\varphi (s)\varphi (t)\), where \(\varphi \) is the function defined on [0, 1], so that it satisfies \(\varphi (0)=\varphi (1)=0\) and \(p=1\), the family \(C_\theta ^{\psi ,p} \) reduce to the symmetric copula introduced by [25].

  6. (vi)

    If \(\psi (s,t)=(1-s^{\alpha })(1-t^{\alpha }),\forall s,t\in [0,1], \alpha \ge 0\), and \(p=n\), where \(n=0,1,2,\ldots \), the family \(C_\theta ^{\psi ,p} \) reduce to the asymmetric extended FGM copula introduced by [5].

  7. (vii)

    If \(\psi (s,t)=(1-s^{\alpha })(1-t^{\beta }),\forall s,t\in [0,1], \alpha>0,\beta >0\), and \(p=n\), where \(n\ge 1\), the family \(C_\theta ^{\psi ,p} \) reduce to the asymmetric extended FGM copula introduced by [23].

  8. (viii)

    If \(\psi (s,t)=f(s^{\frac{1}{n}})g(t^{\frac{1}{n}}),\forall s,t\in [0,1]\), with \(f(1)=g(1)=0\), and \(p=n\), where \(n=1,2,3,\ldots \), the family \(C_\theta ^{\psi ,p} \) reduce to the asymmetric extended FGM copula introduced by [24].

Moreover, via the family \(C_\theta ^{\psi ,p} \), some new generalizations can be defined by introducing the additional parameter p for the families (i)–(v), and we can generate some copulas of the family \(C_\theta ^{\psi ,p} \) through the function \(\psi \).

Proposition 3.1

Two limiting properties of the family \(C_\theta ^{\psi ,p} \)are as follows:

  1. (i)

    \(\mathop {\lim }\nolimits _{p\rightarrow 0} C_\theta ^{\psi ,p} (s,t)=\mathop {\lim }\nolimits _{p\rightarrow 0} st \left[ {1+\theta \psi \left( {s,t} \right) } \right] ^{ p}=st=\Pi (s,t),\) where \(\Pi (s,t)\) is the independent copula,

  2. (ii)

    Let \(\theta =\frac{\delta }{p}\), where \(\delta \le p\), then

    $$\begin{aligned} \begin{aligned} \mathop {\lim }\limits _{{p \rightarrow \infty }} C_{\theta }^{{\psi ,\delta }} (s,t)&= \mathop {\lim }\limits _{{p \rightarrow \infty }} st\left[ {1 + \frac{\delta }{p}\psi (s,t)} \right] ^{p} \\&= \mathop {\lim }\limits _{{p \rightarrow \infty }} st\left[ {1 + \frac{\delta }{p}\psi (s,t)} \right] ^{p} \\&= st\exp [\delta \psi (s,t)] \\&= C_{{\psi ,\delta }} (s,t). \end{aligned} \end{aligned}$$
    (3.1)

The new family \(C_{\psi ,\delta }\) can be a new symmetric generalization of the Gumbel-Barnett (GB) copula discussed by [16], when \(\psi (s,t)=\ln (s)\ln (t),\forall s,t\in [0,1]\) and Celebioglu-Cuadras copula introduced by Cuadras ([9, 10]), when \(\psi (s,t)=(1-s)(1-t)\),\(\forall s,t\in [0,1]\). Also, the copula \(C_{\psi ,\delta } \) can be considered as a new generalization for [18] copula. [18] under some conditions introduced some families of copulas that are closed under the construction of generalized linear means. One of these families has the form:

$$\begin{aligned} C^{\phi }(s,t)=st\exp \left( {\delta \phi (s)\phi (t) } \right) , \forall s,t\in [0,1], \end{aligned}$$

where \(\phi \) is a function that defined on \(I=[0,1]\) and \(\phi \) is satisfied in \(\phi (1)=0\).

4 Measures of dependence

Measures of dependence are common instruments to summarize a complicated dependence structure in the bivariate case. For a historical review of measures of dependence, see [17] and [21]. In this section, we compute the measures of dependence for the family \(C_\theta ^{\psi ,p} \). Since we cannot give formulas for the properties of dependence in terms of elementary functions, it is replaced by its expansion series on

$$\begin{aligned} \Omega =\left\{ { (\theta ,\psi ): \left| {\theta \psi (s,t)} \right| \le 1} \right\} , \forall s,t\in [0,1]. \end{aligned}$$

Based on \(\Omega \), the family \(C_\theta ^{\psi ,p} \) in (2.1), for every \(p\in [1 , \infty )\) may also be written by polynomial expansion with respect to \(\psi \) as

$$\begin{aligned} \begin{aligned} C_{\theta }^{{\psi ,p}} (s,t)&= st\sum \limits _{{k = 0}}^{p} {\left( {\begin{array}{l} p \\ k \\ \end{array} } \right) \theta ^{k} \psi ^{k} (s,t)} \\&= st + \sum \limits _{{k = 1}}^{p} {\left( {\begin{array}{l} p \\ k \\ \end{array} } \right) \theta ^{k} st\psi ^{k} (s,t)} \\ \end{aligned} \end{aligned}$$
(4.1)

Note that, in (4.1), p is an integer, otherwise, p equals to \(+\infty \). Moreover, the family density \(c_\theta ^{\psi ,p} \)in (2.2) can be written as

$$\begin{aligned} c_\theta ^{\psi ,p} (s,t)= & {} \sum \limits _{k=0}^{ p-2} {\left( {{ \begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}\psi ^{k}(s,t) \nonumber \\&\times \left\{ { \left( {1+\theta \psi (s,t)} \right) ^{2}+} \right. p\theta \left( {1+\theta \psi (s,t)} \right) \left[ {s\psi _s (s,t)+t\psi _t (s,t)+st\psi _{st} (s,t) } \right] \nonumber \\&\left. {+p(p-1) \theta ^{2}s \psi _s (s,t) t \psi _t (s,t)} \right\} . \end{aligned}$$
(4.2)

Proposition 4.1

Let (X, Y) be a pair of random variables with distribution belonging to the family \(C_\theta ^{\psi ,p} \) and the density family \(c_\theta ^{\psi ,p}\). Then

$$\begin{aligned}&E\left[ {\psi (S,T)} \right] = \sum \limits _{k=0}^{ p-2} {\left( \begin{array}{l} p \\ k \\ \end{array}\right) }\theta ^{k}\left\{ d_1 (0,k+1)+\theta \left( {2-\frac{p}{k+2}} \right) d_1 (0,k+2)\right. \nonumber \\&\left. \qquad \qquad \qquad \qquad +\theta ^{2}\left( {1 -\frac{p}{k+3}} \right) d_1 (0,k+3) \right. \nonumber \\&\left. {\qquad \qquad \qquad \qquad -(k+1)p\theta d_2 (1,k)+p\theta ^{2}\left( {p-k-3} \right) d_2 (1,k+1)} \right\} , \end{aligned}$$
(4.3)

where \(d_1 (a,k)=\int \limits _0^1 {\int \limits _0^1 {s^{a}t^{a} \psi ^{k}(s,t) ds\, dt}}\) and \(d_2 (a,k)=\int \limits _0^1 \int \limits _0^1 s^{a} \psi _s (s,t) t^{a} \psi _t (s,t)\) \(\psi ^{k}(s,t) ds\, dt\).

Proof

by using (4.2), \(E\left[ {\psi (S,T)} \right] \) can be expanded as

$$\begin{aligned} \begin{array}{l} \displaystyle E\left[ {\psi (S,T)} \right] =\sum \limits _{k=0}^{ p-2} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}\int \limits _0^1 {\int \limits _0^1 {\psi ^{k+1}(s,t)\left\{ { \left( {1+\theta \psi (s,t)} \right) ^{2}} \right. } } \\ \qquad \qquad \qquad \qquad \, \displaystyle +p\theta \left( {1+\theta \psi (s,t)} \right) \left[ {s\psi _s (s,t)+t \psi _t (s,t)+st \psi _{st} (s,t) } \right] \\ \left. {\qquad \qquad \qquad \qquad \, \displaystyle +p(p-1) \theta ^{2}s \psi _s (s,t)t \psi _t (s,t)} \right\} ds\, dt \\ \qquad \qquad \qquad \,\, \displaystyle =\sum \limits _{k=0}^{ p-2} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}\left\{ {\int \limits _0^1 {\int \limits _0^1 {\left( {\psi ^{k+1}(s,t)+2 \theta \psi ^{k+2}(s,t)+\theta ^{2}\psi ^{k+3}(s,t)} \right) ds\, dt} } } \right. \\ \quad \qquad \qquad \qquad \quad \displaystyle +p\theta \left( {\int \limits _0^1 {\int \limits _0^1 {s \psi _s (s,t) \psi ^{k+1}(s,t)ds\,dt+\int \limits _0^1 {\int \limits _0^1 {t \psi _t (s,t) \psi ^{k+1}(s,t) ds\, dt} } } } } \right) \\ \quad \qquad \qquad \qquad \quad \displaystyle +p\theta ^{2}\left( {\int \limits _0^1 {\int \limits _0^1 {s \psi _s (s,t) \psi ^{k+2}(s,t)ds\, dt+\int \limits _0^1 {\int \limits _0^1 {t \psi _t (s,t) \psi ^{k+2}(s,t) ds\, dt} } } } } \right) \\ \quad \qquad \qquad \qquad \quad \displaystyle +p\theta \left( {\int \limits _0^1 {\int \limits _0^1 {st \psi _{st} (s,t) \psi ^{k+1}(s,t)ds\, dt+\theta \int \limits _0^1 {\int \limits _0^1 {st \psi _{st} (s,t) \psi ^{k+2}(s,t) ds\, dt} } } } } \right) \\ \quad \qquad \qquad \qquad \quad \displaystyle \left. { +p(p-1) \theta ^{2}\int \limits _0^1 {\int \limits _0^1 {s \psi _s (s,t)t \psi _t (s,t) \psi ^{k+1}(s,t) ds\, dt} } } \right\} . \\ \end{array} \end{aligned}$$

Using part by part integration (Appendix A.), we have

$$\begin{aligned}&\int \limits _0^1 {\int \limits _0^1 {s \psi _s (s,t) \psi ^{k+1}(s,t) ds dt=\int \limits _0^1 {\int \limits _0^1 {t\psi _t (s,t) \psi ^{k+1}(s,t) ds \,dt=} } -} } \frac{1}{k+2}d_1 (0,k+2),\\&\int \limits _0^1 {\int \limits _0^1 {s\psi _s (s,t) \psi ^{k+2}(s,t) ds\, dt} } =\int \limits _0^1 {\int \limits _0^1 {t\psi _t (s,t) \psi ^{k+2}(s,t) ds\, dt=-\frac{1}{k+3}} } d_1 (0,k+3),\\&\quad \int \limits _0^1 {\int \limits _0^1 {st \psi _{st} (s,t) \psi ^{k+1}(s,t) ds\, dt=\frac{1}{k+2}d_1 (0,k+2)-(k+1) d_2 (1,k)} } , \end{aligned}$$

and

$$\begin{aligned} \int \limits _0^1 {\int \limits _0^1 {st \psi _{st} (s,t) \psi ^{k+2}(s,t) ds dt=\frac{1}{k+3}d_1 (0,k+3)-(k+2)d_2 (1,k+1)} } . \end{aligned}$$

So,

$$\begin{aligned} E\left[ {\psi (S,T)} \right]= & {} \sum _{k=0}^{ p-2} {\left( \begin{array}{l} p \\ k \\ \end{array}\right) }\theta ^{k}\left\{ d_1 (0,k+1)+2 \theta d_1 (0,k+2)+\theta ^{2}d_1 (0,k+3)\right. \\&\left. -\frac{2p\theta }{k+2}d_1 (0,k+2) -\frac{2p\theta ^{2}}{k+3}d_1 (0,k+3) \right. \\&+p\theta \left( \frac{1}{k+2}d_1 (0,k+2)-(k+1)d_2 (1,k)+\theta \right. \\&\times \left. \left[ {\frac{1}{k+3}d_1 (0,k+3)-(k+2) d_2 (1,k+1)} \right] \right) \\&\left. {+p(p-1) \theta ^{2}d_2 (1,k+1)} \right\} \\= & {} \sum \limits _{k=0}^{ p-2} {\left( \begin{array}{l} p \\ k \\ \end{array}\right) } \theta ^{k}\left\{ d_1 (0,k+1)+\theta \left( {2-\frac{p}{k+2}} \right) d_1 (0,k+2)\right. \\&+\theta ^{2} \left( {1 -\frac{p}{k+3}} \right) d_1 (0,k+3) \\&\left. {-(k+1)p\theta d_2 (1,k)+p\theta ^{2}\left( {p-k-3} \right) d_2 (1,k+1)} \right\} . \end{aligned}$$

\(\square \)

Example 4.1

For \(\psi (s,t)=(1-s)(1-t), \forall s,t\in [0,1]\) and \(p=1\)in (2.1), the classical FGM copula, we have \(E\left[ {(1-S)(1-T)} \right] =\theta /{36}+1/4,\, \mathrm{cov}\,(S,T)=\theta /{36}\), and the correlation coefficient is \(\rho =\theta /3\).

4.1 Spearman’s rho

Let X and Y be continuous random variables whose copula is C. Then the population version of Spearman’s rho for X and Y is given by

$$\begin{aligned} \rho _S =12\int \limits _0^1 {\int \limits _0^1 {C(s,t) ds\, dt-3} } . \end{aligned}$$

Note that, \(\rho _S\) coincides with the correlation coefficient \(\rho \) between the uniform marginal distributions.

Proposition 4.2

Let (X, Y) be a pair of random variables with distribution belonging to the family \(C_\theta ^{\psi ,p} \). The Spearman’s rho for the family \(C_\theta ^{\psi ,p} \)is given by

$$\begin{aligned} \rho _S =12\sum _{k=1}^{ p} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}d_1 (1,k). \end{aligned}$$
(4.4)

Proof

by using (4.1), the Spearman’s rho can be expanded as

$$\begin{aligned} \begin{array}{l} \displaystyle \rho _S =12\int \limits _0^1 {\int \limits _0^1 {C_\theta ^{\psi ,p} (s,t) ds\, dt} } -3 \\ \displaystyle \qquad =12\left\{ {\int \limits _0^1 {\int \limits _0^1 {st\, ds\, dt} } +\int \limits _0^1 {\int \limits _0^1 {\sum _{k=1}^{ p} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) \theta ^{k}st \psi ^{k}(s,t)} ds\, dt} } } \right\} -3 \\ \displaystyle \qquad =12\int \limits _0^1 {\int \limits _0^1 {st\, ds \,dt} } +12\int \limits _0^1 {\int \limits _0^1 {\sum _{k=1}^{ p} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) \theta ^{k}st \psi ^{k}(s,t)} ds\, dt} } -3 \\ \displaystyle \qquad =12\sum _{k=1}^{ p} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}\int \limits _0^1 {\int \limits _0^1 {st\psi ^{k}(s,t) ds\, dt} } \\ \displaystyle \qquad =12\sum _{k=1}^{ p} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}d_1 (1,k) . \\ \end{array} \end{aligned}$$

\(\square \)

4.2 Kendall’s tau

In terms of copula, Kendall’s tau \(\tau _k \) is defined as (see [21])

$$\begin{aligned} \tau _k =4\int \limits _0^1 {\int \limits _0^1 {c(s,t) C(s,t) ds\, dt-1} } . \end{aligned}$$

Proposition 4.3

Let (X, Y) be a pair of random variables with the family \(C_\theta ^{\psi ,p} \) and the density family \(c_\theta ^{\psi ,p} \); then the Kendall’s tau (\(\tau _k\)) can be expanded as

$$\begin{aligned}&\tau _k =4\sum _{k=0}^{ 2p-2} {\left( \begin{array}{l} {2p-2} \\ k \\ \end{array}\right) \theta ^{k}} \left\{ d_1 (1,k)+2\theta \left( {1-\frac{p}{k+1}} \right) d_1 (1,k+1)\right. \nonumber \\&\left. \qquad \quad +\theta ^{2}\left( {1-\frac{2p}{k+2}} \right) d_1 (1,k+2) \right. -k\, p\theta d_2 (2,k-1) \nonumber \\&\left. {\qquad \quad +p\theta ^{2}(p-k-2) d_2 (2,k)} \right\} -1 . \end{aligned}$$
(4.5)

Proof

The proof of this proposition was deferred to the Appendix B. \(\square \)

4.3 Gini’s gamma and the Spearman’s footrule coefficient

Let X and Y be continuous random variables whose copula is C, then the population version of Gini’s gamma (\(\gamma _C\)) and Spearman’s footrule coefficient (\(\delta _C\)) for X and Y are given by

$$\begin{aligned} \gamma _C =4\int \limits _0^1 {\left[ {C(s,s)+C(s,1-s)} \right] ds-1} \end{aligned}$$

and

$$\begin{aligned} \delta _C =6\int \limits _0^1 {C(s,s) ds-2} , \end{aligned}$$

respectively.

Proposition 4.4

Let (X, Y) be a pair of random variables with distribution belonging to the family \(C_\theta ^{\psi ,p} \) and the density family \(c_\theta ^{\psi ,p} \); then the direction of equality between Gini’s gamma (\(\gamma _C )\) and the Spearman’s footrule (\(\delta _C )\) is given by

$$\begin{aligned} 3\gamma _C -2\delta _C =3+12 \sum _{k=1}^{ p} {\left( {{\begin{array}{l} p \\ k \\ \end{array} }} \right) } \theta ^{k}\int \limits _0^1 { \left[ { s(1-s) \psi ^{k}(s , 1-s)} \right] } ds. \end{aligned}$$
(4.6)

Proof

The proof is straightforward \(\square \)

Remark 4.1

For \(\psi (s,t)=(1-s)(1-t)\) and \(p=1\) in (2.1), the classical FGM copula, we have \(\rho _S =\theta /3,\tau _k =2\theta /9\), and \(3\gamma _C -2\delta _C =3+{2\theta }/5\). Hence, we have \(-0.33\le \rho _S \le \hbox {0.33}\) and \(-0.22\le \tau _k \le 0.22\)(as\(-1\le \theta \le 1\)).

As the remark (4.1) shows, the domain of correlation of FGM copula is limited and therefore it is not allowed for modeling of strong dependence. One of the advantages of the family \(C_\theta ^{\psi ,p} \) is capability to improve the domain of correlation by introducing additional parameter p in FGM copula and some generalized FGM families presented in recent years.

Example 4.2

In the family \(C_\theta ^{\psi ,p}\), let \(\psi (s,t)=(1-s)(1-t)\). Then the family \(C_\theta ^{\psi ,p}\) leads to a new symmetric generalized FGM copula with \(-\left( {\max \{1,p\}} \right) ^{-1}\le \theta \le p^{-1}\). Since

$$\begin{aligned} d_1 (1,k)=\int \limits _0^1 {\int \limits _0^1 {st\psi ^{k}(s,t)dsdt=\left( {\frac{1}{(k+1)(k+2)}} \right) ^{2}} } , \end{aligned}$$

we have by using (4.4) that

$$\begin{aligned} \rho _S =12\sum _{k=1}^{ p} {\left( {{ \begin{array}{l} p \\ ssk \\ \end{array} }} \right) } \theta ^{k}\left[ {\frac{1}{(k+1)(k+2)}} \right] ^{ 2}, \end{aligned}$$

where the upper bound of above \(\rho _S\) can be increased up to approximately 0.3805 as \(p\rightarrow \infty \), while the lower bound −0.3333 remains unchanged. Therefore, the admissible range of \(\rho _S \) in the new symmetric generalized FGM family is \([-0.3333 , 0.3805]\).

Example 4.3

In the family \(C_\theta ^{\psi ,p}\), let \(\psi (s,t)=(1-s^{\alpha })(1-t^{\alpha }),\alpha \ge 0\). Then the family \(C_\theta ^{\psi ,p}\) leads to a new symmetric generalized Hung-Kotz family with \(-\left( {\max \{1,p\alpha ^{2}\}} \right) ^{-1}\le \theta \le (p\alpha )^{-1}\). Since

$$\begin{aligned} d_1 (1,k)=\int \limits _0^1 {\int \limits _0^1 {st \psi ^{k}(s,t) ds dt=\left( {\frac{\Gamma \left( {k+1} \right) \Gamma \left( {2/\alpha } \right) }{\alpha \Gamma \left( {k+1+2/\alpha } \right) }} \right) ^{2}} } , \end{aligned}$$

we have

$$\begin{aligned} \rho _S =12\sum _{k=1}^{ p} {\left( {{ \begin{array}{l} p \\ k \\ \end{array} }} \right) \theta ^{k}} \left( {\frac{\Gamma \left( {k+1} \right) \Gamma \left( {2/\alpha } \right) }{\alpha \Gamma \left( {k+1+2/\alpha } \right) }} \right) ^{2}\quad . \end{aligned}$$
(4.7)

Taking \(\alpha \cong 1.85\) and \(p>500\) in (4.7), we have \(\rho _{S,\max } =0.43\). Similarly, taking \(\alpha \cong 0.1\) and \(p>500\), we obtain \(\rho _{S,\min } \cong -0.50\). Therefore, the admissible range of \(\rho _S\) in the generalized Hung-Kotz family is \([-0.50 , 0.43]\). So, the generalized Hung-Kotz copula improves the amplitude \(\rho _S\) of Hung-Kotz family.

4.4 Tail dependence

The concept of tail dependence relates to the amount of dependence in the upper-right quadrant tail and the lower-left-quadrant tail of a bivariate distribution. It is a concept that is relevant for the study of dependence between extreme values. It turns out that tail dependence between two continuous random variables X and Y is a copula property and hence the amount of tail dependence is invariant under strictly increasing transformations of X and Y ([8, 14, 17]). For a bivariate copula C if

$$\begin{aligned} \lambda _U =\mathop {\lim }\limits _{s\rightarrow 1^{-}} \frac{1-2s+C(s,s)}{1-s}, \end{aligned}$$
(4.8)

exists, then C has upper tail dependence if \(\lambda _U \in (0,1]\), and upper tail independence if \(\lambda _U =0\). The measure is extensively used in Extreme value theory. The concept of lower tail dependence can be defined in a similar way. If the limit,

$$\begin{aligned} \lambda _L =\mathop {\lim }\limits _{s\rightarrow 0^{+}} \frac{C(s,s)}{s}, \end{aligned}$$
(4.9)

exist, then C has lower tail dependence if \(\lambda _L \in (0,1]\), and lower tail independence if \(\lambda _L =0\).

Proposition 4.5

Let (X, Y) be a pair of random variables with distribution belonging to the family \(C_\theta ^{\psi ,p}\); then for the copula \(C_\theta ^{\psi ,p} \), we have

$$\begin{aligned} \lambda _u =-p\theta \left[ { \psi _{s,1} (1,1)+\psi _{s,2} (1,1)} \right] , \end{aligned}$$
(4.10)

and

$$\begin{aligned} \lambda _L =0. \end{aligned}$$
(4.11)

Proof

Clearly, the upper tail dependence coefficient (\(\lambda _U )\) can be simplified as

$$\begin{aligned} \lambda _U =\mathop {\lim }\limits _{u\rightarrow 1^{-}} \frac{1-2s+s^{2}[1+\theta \psi (s,s)]^{p}}{1-s}, \end{aligned}$$

so,

$$\begin{aligned} \begin{array}{l} \lambda _U =\mathop {\lim }\limits _{s\rightarrow 1^{-}} \left( {1-\frac{s \left\{ { 1-[1+\theta \psi (s,s)]^{p}} \right\} }{1-s}} \right) \\ \qquad =1-\mathop {\lim }\limits _{s\rightarrow 1^{-}} s \left[ {\frac{[1+\theta \psi (1,1)]^{p}-s[1+\theta \psi (s,s)]^{p}}{1-s}} \right] \\ \qquad =1-\mathop {\lim }\limits _{s\rightarrow 1^{-}} \left[ {\frac{\partial }{\partial s}s [1+\theta \psi (s,s)]^{p}} \right] \\ \qquad =1-\mathop {\lim }\limits _{s\rightarrow 1^{-}} \left( { [1+\theta \psi (s,s)]^{p}} \right) -p\theta \mathop {\lim }\limits _{u\rightarrow 1^{-}} s[ \psi _{1,s} (s,s)+\psi _{2,s} (s,s)][1+\theta \psi (s,s)]^{p-1} \\ \qquad =-p\theta \mathop {\lim }\limits _{s\rightarrow 1^{-}} \left[ {\psi _{s,1} (s,s)+\psi _{s,2} (s,s)} \right] \\ \qquad =-p\theta \left[ {\psi _{s,1} (1,1)+\psi _{s,2} (1,1)} \right] . \\ \end{array} \end{aligned}$$

Also, the lower tail dependence coefficient (\(\lambda _L\)) can be simplified by replacing (2.1) in (4.9) as

$$\begin{aligned} \begin{array}{l} \lambda _L =\mathop {\lim }\limits _{s\rightarrow 0^{+}} \frac{s^{2}[1+\theta \psi (s,s)]^{p}}{s} \\ \qquad =\mathop {\lim }\limits _{s\rightarrow 0^{+}} s[1+\theta \psi (s,s)]^{p} , \\ \end{array} \end{aligned}$$

where \(\lambda _L\) is indeterminate as \([1+\theta \psi (s,s)]^{p}\) tends to \(+\infty \), otherwise \(\lambda _L =0\). \(\square \)

In (4.8) the copula \(C_\theta ^{\psi ,p}\) is a one-parameter family of copulas whose upper tail dependence coefficient (\(\lambda _u)\) ranges from 0 to 1 through function \(\psi \).

Example 4.4

Choosing \(\psi (s,t)\) as the cumulative distribution function of the uniform distribution on \([0,\theta ]\), \(\theta \le 1\), introduced in [15], gives the new family of copulas

$$\begin{aligned} C_\theta ^{\psi ,p} (s,t)\!=\!st(1\!+\!\theta \min (1-s,1-t))^{p}, p\in [1,\infty ), \quad 0\!\le \!\theta \!\le \!p^{-1}, \mathrm{and}\, \forall (s,t)\in [0,1]^{2}. \end{aligned}$$

By using (4.8), in this new family, we have

$$\begin{aligned} \lambda _U =p\theta \in [0,1]. \end{aligned}$$

Example 4.5

Consider the function \(\psi (s,t)=\min (s,t)\,f(\max \{s,t\}),\forall (s,t)\in [0,1]^{2}\), where \(f(1)=0\) in (2.1); this leads to a new copula as follows:

$$\begin{aligned} C_\theta ^{\psi ,p} (s,t)=s t (1+\theta \min (s,t)\,f(\max \{s,t\}))^{p}, p\in [1,\infty ). \end{aligned}$$

By using (4.8), in this new family, we have

$$\begin{aligned} \lambda _U =-p\theta {f}^{\prime }(1). \end{aligned}$$

Example 4.6

Consider the function \(\psi (s,t)=f_1 (s)f_2 (t),\forall (s,t)\in [0,1]^{2}\), so that \(f_1 (1)=f_2 (1)=0\)in (2.1), that leads to a new copula as follows:

$$\begin{aligned} C_\theta ^{\psi ,p} (s,t)=st(1+\theta _1 f_1 (s)f_2 (t))^{p}, p\in [1,\infty ). \end{aligned}$$

By using (4.8), in this new family, we have

$$\begin{aligned} \lambda _U =0. \end{aligned}$$

Based on these examples, we can state the following result:

Corollary 4.1

Let (X, Y) be a pair of random variables with the family \(C_\theta ^{\psi ,p} \) and \(\psi \left( {s,1} \right) =\psi \left( {1,s} \right) =0\), for every \(s\in [0,1]\). Thus, \(0\le \lambda _u \le 1\) and this bound is reached within the sub-families, while for FGM copula \(\lambda _U =0\).

5 Application and simulation

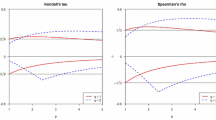
In this section, we apply our presented generalized FGM copula to some real dataset in medical science. According to the manual of R’s package MASS, the US National Institute of Diabetes and Digestive and Kidney Diseases collected data set from a population of women (at least 21 years old, of Pima Indian heritage and living near Phoenix, Arizona) who were tested for diabetes based on World Health Organization criteria. This dataset was later reanalyzed by [20]. This dataset consists of 200 complete records after dropping the data on serum insulin. Information is needed in analysis and management of body health test, the most important part of which is the study of features frequency of Body Mass Index (BMI) and Diabetes Pedigree Function (PED). Now, let us model the dependence between BMI and PED. Considering the correlation of these two features, some tools must be used to reveal the amount of relationship and impact which exists in the analysis; therefore it is necessary to determine the joint distribution of the two features, BMI and PED. Because of the association amount suggested by the correlation coefficient of 0.172, we reject independent assumption between two variables \((sig.=0.015)\). According to the low correlation coefficient between BMI and PED, we decide to determine dependency structure and bivariate distribution between BMI and PED through fitting FGM copula and presented generalized FGM copula in this paper. To this end and to be free of determining marginals distribution; we use Kernel method to determine marginals distribution for BMI and PED before further analyzing. Hereafter, we use S and T instead of cumulative distribution function BMI and PED, respectively, which determine using Kernel method. For estimating parameter of generalized FGM copula in (2.1), \(\theta \) and p, the log-likelihood function was computed. The results for different function \(\psi \) and parameter estimation with AIC criteria are presented in Table 1. This table shows the family\(C_\theta ^{\psi ,p} \) is the flexible generalized FGM copula, by choosing different types of \(\psi \) functions and estimating parameter \(\theta \) and p; accordingly, the family \(C_\theta ^{\psi ,p} \) can better fit the interested medical data. As an example, for \(\psi =s(1-s)(1-t), \theta =0.1553\) and \(p=3.5237 (p>1)\) the family \(C_\theta ^{\psi ,p} \) shows \(\psi \) has less AIC. These results can be investigated using simulation and scatter plot study. Also, in order to evaluate and compare the detailed functions Table 1, the main measure of proximity to the empirical joint distribution of data is used, that results of this evaluation and comparison are summarized in Fig. 1. Figure 1 shows that the joint model III is closer to the main points, therefore, the empirical joint distribution function III, is more suitable for fitting to the data Fig. 2.

Table 1 Different models of the generalized FGM copula
Full size table
Fig. 1
figure 1

Plots of the empirical joint distribution from the generalized FGM copula model

Full size image
Fig. 2
figure 2

Graph of the generalized family for \(\psi (s,t)=s(1-s)(1-t)\) for \(p=3.5237\) and \(\theta =0.1553\)

Full size image

The Graph of the generalized family for \(\psi (s,t)=s(1-s)(1-t)\) for \(p=3.5237\) and \(\theta =0.1553\) is as follows:

Also, in Fig. 3, the contour plots for the functions of Table 1 are drawn.

Fig. 3
figure 3

Contour plots of the generalized FGM copula model

Full size image

We now discuss the simulation of data from the generalized FGM family and perform comparisons between correlations in the simulated data and in the observed data based on 1000 simulations. We follow the simulation method proposed by Johnson (1987, Ch.3) and later Nelson (2006, page 41). Thus, a sampling algorithm to simulate from \(C_\theta ^{\psi ,p} (s_1 ,t_1 )\) is as follows:

  1. (1)

    Draw two independent uniform random values \((s_1 ,t_2 )\).

  2. (2)

    Set \(t_1 =C_{2\left| 1 \right. }^{-1} (s_1 ,t_2 )\), where \(C_{2\left| 1 \right. }^{-1} \) denotes the pseudo-inverse of \(C_{2\left| 1 \right. } \).

The vector \((s_1 ,t_1 )\) is generated from the family \(C_\theta ^{\psi ,p} \).

Figure 4, Sub-Figure (I) to (III), illustrates the scatter plots of the transformed observed data (o) versus simulated samples of the CDFs of BMI and PED variables (*) taken from the fitted generalized FGM copula in Table 1. It can almost be seen that the simulated data and the original data have similar dependence patterns but the consistency amount between observed data and simulated data is not so clear in Sub-Figures of Fig. 1. To settle this concern, Table 2 shows the rank correlations between the BMI and PED variables calculated from the original observed data, and based on the simulated data of size 1000 taken from the fitted FGM copula; and the generalized FGM copula family. By comparing these correlations, we can conclude that the results show strong consistency of the estimated correlations based on the generalized FGM copula are closer to the ones which come from the observed data.

Fig. 4
figure 4

Scatter plots of the transformed observed values versus simulated samples of BMI and PED variables from the generalized FGM copula model

Full size image
Table 2 Calculated correlations for different models of the generalized FGM copula
Full size table