Abstract
Introduction
Schizophrenia is a chronic mental disorder that worsens with each relapse. Long-acting injectable (LAI) antipsychotics may prevent the exacerbation of symptoms and occurrence of relapses through improved continuity of care. Different dose regimens are available for the LAIs aripiprazole monohydrate (AM) and aripiprazole lauroxil (AL), but their cost effectiveness is unclear.
Objectives
The study aim was to compare costs and effects (relapses) of the different aripiprazole LAI dose regimens to inform clinical and US payer decisions.
Methods
A state-transition model calculated the outcomes of eight LAI dose regimens based on their relapse rates. As effectiveness data from randomized controlled trials were unavailable, relapse rates were modeled using pharmacokinetic and pharmacodynamic evidence. These described blood plasma levels of aripiprazole as a function of AM and AL dose regimens and described the probability of relapse as a function of aripiprazole blood plasma levels. The analysis had a time horizon of 1 year and took the US healthcare payer perspective. The incremental cost per relapse avoided and the probability of cost effectiveness were calculated in deterministic and probabilistic analyses. Scenario analyses explored the model’s main assumptions, and results were validated against external data and other cost-effectiveness analyses.
Results
Monthly administration of AM 400 mg consistently yielded the lowest predicted number of relapses across deterministic, probabilistic, and scenario analyses. The costs of treatment and relapses were projected to be the lowest with a monthly administration of AL 441 mg. The incremental cost per relapse avoided with AM 400 mg ranged from AM 400 mg being dominant to $US83,300. From willingness-to-pay thresholds of $US30,000 per relapse avoided, the probability of cost effectiveness was highest for AM 400 mg. The validation showed alignment with external data.
Conclusion
The analysis highlighted the robustness of the novel framework based on pharmacokinetic and pharmacodynamic evidence and demonstrated an application in a postmarketing setting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
The application of pharmacokinetic and pharmacodynamic evidence provided a flexible modeling framework as well as robust results, as shown by the successful validation. The framework has potential for further application in other therapies and disease areas with similar data restrictions, which is relevant for model-informed drug development programs. |
The findings may help physicians and US payers make informed decisions considering both the clinical and the economic consequences of the different available long-acting injectable dose regimens in patient care. |
1 Introduction
Schizophrenia is a chronic mental disorder characterized by acute phases of positive symptoms (e.g. hallucinations, delusions, and behavioral disturbances) as well as negative symptoms (e.g. lack of emotion, reduced interest in day-to-day activities, and social withdrawal). These symptoms are often present even in stable phases, although they often worsen during acute exacerbations or relapses. Repeated relapses may cause the functioning of patients to deteriorate further [3]. Relapse prevention is therefore a fundamental element in the management of schizophrenia [4].
Maintenance treatment with regular long-term use of antipsychotic medication [4, 5] and continuity of care is essential in the prevention of relapses [6,7,8]. Poor adherence and its associated fluctuations in blood plasma levels of treatment medications is a critical factor in the poor outcomes experienced by some patients [9, 10] and has been linked with symptom exacerbation, disease relapse, and increased need for hospitalization [11].
Long-acting injectable (LAI) antipsychotics avoid the need to take oral medication every day and may, as such, be more effective than oral antipsychotics in improving medication adherence and persistence [6, 10]. Aripiprazole monohydrate (AM) [12] and aripiprazole lauroxil (AL), a prodrug that is converted to aripiprazole [13], are LAI formulations of aripiprazole with different pharmacokinetic profiles. Different dose regimens of AM and AL are currently used for the maintenance treatment of adults with schizophrenia [12, 13], and clinical data have shown that these result in varying steady-state average aripiprazole plasma concentrations (Cavg) [14].
The aim of this study was to compare the costs and effects, specifically relapses, of the available aripiprazole LAI dose regimens and, in particular, to assess the consequences of different frequencies of administration to inform clinical and US payer decisions. Pharmacoeconomic models comparing the costs and effects of different treatment options typically rely on comparative long-term outcome data from phase III randomized controlled trials (RCTs). This type of evidence is not, and likely will not be, available for all the AL doses in the current comparison, as two dose regimens (662 and 1064 mg) were granted US FDA approval based on combining phase I pharmacokinetic data and simulations. The simulated steady-state exposures of these doses were compared with those dose regimens with phase III outcome data supporting their approval using a so-called “bridging approach” [15].
In the absence of RCT data, pharmacometric models can be used to simulate clinical inputs for the pharmacoeconomic analysis [16, 17]. This analysis consists of three sequential components: (1) a pharmacokinetic model characterizing the blood plasma concentrations over time resulting from different aripiprazole LAI dose regimens, (2) a pharmacodynamic model linking these blood plasma levels with relapse rates over time, and (3) a pharmacoeconomic model outlining the health and economic outcomes of the LAI dose regimens, based on the modeled relapse rates. This paper presents an application of a pharmacokinetic–pharmacodynamic–pharmacoeconomic (PK–PD–PE) [17], or pharmacometric–pharmacoeconomic (PMPE) [16], model for the pharmacoeconomic assessment of different aripiprazole LAI dose regimens for the treatment of schizophrenia to inform clinical and payer decisions in the USA in a postmarketing setting.
2 Methods
2.1 Population
The modeled population consisted of adults with schizophrenia, in accordance with the indications of AM and AL [12, 13]. A patient cohort was simulated by bootstrapping the pivotal trial data of AM [18]. The cohort had a mean age of 39 years, a mean height of 170 cm, and mean weight of 81 kg. In total, 36% of the cohort was female, and 5% had a poor cytochrome P450-2D6 metabolizer status.
2.2 Treatments
The analysis compared eight LAI dose regimens: two AM dose regimens (400 or 300 mg every 4 weeks [q4wk]) and six AL dose regimens (441 or 662 or 882 mg q4wk, 882 or 1064 mg every 6 weeks [q6wk], 1064 mg every 8 weeks [q8wk]). Please note that according to expert opinion, in clinical practice, AL 441 mg and AM 300 mg are generally used only when patients do not tolerate higher doses [6]. The model assumed that AM and AL were administered as single intramuscular injections according to the package insert [12, 13]. For the first 14 days of AM treatment and for the first 21 days of AL treatment, oral aripiprazole monohydrate 15 mg daily was administered concomitantly [12, 13]. The model assumed complete adherence to medication. The analysis assumed treatment after discontinuation of LAI was standard of care (SoC), consisting of the oral medications olanzapine, risperidone, quetiapine, and ziprasidone.
2.3 Study Perspective and Time Horizon
The analysis took a US healthcare payer perspective and considered only direct healthcare costs (cost year of 2021). The time horizon was 1 year starting at LAI initiation, a scenario typically relevant for US payers. A scenario analysis evaluated a 2-year time horizon. In line with guidelines, costs were discounted by 3% per year in this scenario [19].
2.4 Model
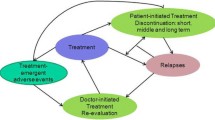
A targeted literature review was conducted to identify published PK–PD–PE models of adults with schizophrenia to inform model structure and model inputs. Figure 1 provides an overview of the model, consisting of the pharmacokinetic, pharmacodynamic, and pharmacoeconomic components, and shows how these are linked together. First, the pharmacokinetic component of the model was used to simulate the aripiprazole plasma concentration over time and the minimum concentration per dosing interval (Cmin) for each LAI dose regimen. Second, the pharmacodynamic component was used to derive the probability of relapse conditional on the simulated aripiprazole Cmin. This served as effectiveness data in the pharmacoeconomic model. The pharmacoeconomic model itself was a Markov patient-level simulation with five health states representing remission on LAI, relapse on LAI, remission on SoC, relapse on SoC, and death. Patients entered the model in the health state “remission on LAI,” where they were treated with an LAI dose regimen. Patients experiencing a relapse moved to the health state “relapse on LAI.” Patients who discontinued LAI moved to “remission on SoC” or “relapse on SoC” if they also experienced a relapse. Patients who recovered from their relapse moved to the “remission” health state. From all health states, patients could move to the absorbing health state “death.” Adverse events were not modeled because evidence regarding adverse events at different Cmin was unavailable and evidence also suggested that the safety profiles of AM and AL were similar [20, 21]. The model had a cycle length of 2 weeks, which was the highest common denominator of the 4-, 6-, and 8-week regimens of the evaluated LAIs, was built in R version 4.0.2 [1], and made use of the RxODE package [2].
Schematic model overview of the PK–PD–PE model, structure of the pharmacoeconomic model. AL aripiprazole lauroxil, AM aripiprazole monohydrate, BL baseline, Cmin minimum aripiprazole plasma concentration per dosing interval, LAI long-acting injectable, PD pharmacodynamic, PE pharmacoeconomic, PK pharmacokinetic, SoC standard of care
2.5 Outcomes
The following (interim) outcomes were generated.
-
In the pharmacokinetic model:
-
o
the minimum aripiprazole plasma concentration per dosing interval, i.e. Cmin
-
o
-
In the pharmacodynamic model:
-
o
the probability of relapse per patient over time based on Cmin over time, and
-
o
the average number of relapses per treatment regimen within the time horizon.
-
o
-
In the pharmacoeconomic model:
-
average cost per patient, total and per cost category (costs of relapses; costs during treatment with LAI or with SoC, including drug acquisition; and disease management and administration costs),
-
number of relapses avoided,
-
cost per relapse avoided, and
-
cost-effectiveness acceptability curve (CEAC) based on willingness to pay (WTP) per relapse avoided
2.6 Effectiveness Estimation
2.6.1 Pharmacokinetic Models
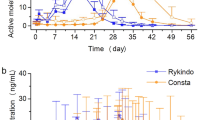
Two pharmacokinetic models, one for each LAI, were selected based on methodological robustness and similarity in model structures [18, 22]. Both pharmacokinetic models were published by the respective manufacturers and based on clinical trials. The pharmacokinetic model for AM was a three-compartment model with one central and two peripheral compartments [18]. The pharmacokinetic model for AL was a two-compartment model with one central and one peripheral compartment [22]. In both models, the absorption of aripiprazole from the oral depot during the initiation phase was described by a first-order process [18, 22]. In the AM pharmacokinetic model, the absorption of aripiprazole from the intramuscular depot was modeled by a first-order process to reflect the bolus injection [18]. In the AL pharmacokinetic model, the enzymatic conversion of AL to aripiprazole was described by a zero-order process with lag time, and the absorption of aripiprazole was modeled by a first-order process [22]. Details of the equations used can be found in electronic supplementary material (ESM)-1. Both models were built in NONMEM software and were replicated in R for seamless integration with the pharmacodynamic and pharmacoeconomic elements.
The pharmacokinetic parameters were dependent on a set of covariates that were randomly bootstrapped for each simulated patient and subject to uncertainty. The Cmin of each simulated patient during each dosing interval following different LAI regimens was simulated based on the patients’ baseline characteristics and the administered LAI dose regimen.
2.6.2 Pharmacodynamic Model
Based on the estimated Cmin values from the aforementioned pharmacokinetic models, a pharmacodynamic model characterizing the relationship between aripiprazole Cmin and relapse was used to derive the probability of relapse for each simulated patient during each dosing interval. The pharmacodynamic model was developed using SAS software [23] by the sponsor of this study using data from 315 patients receiving either placebo or 300/400 mg AM. It modeled relapse probability as a function of aripiprazole Cmin using a survival model with an exponential hazard function [24]. The proportional hazard assumption did not hold for a continuous hazard function. A dichotomous hazard function with a cut-off value of Cmin = 95 ng/mL was used in line with previous analyses [14]. Different models were fitted, and the exponential hazard function was chosen based on goodness-of-fit statistics. As an alternative scenario, a continuous hazard rate as a function of Cmin was fitted. The hazard rates generated were transformed into a 14-day relapse probability to match with the model’s cycle length. The probability of transition from remission to relapse with LAI treatment could therefore be calculated conditional on the estimated Cmin value of each simulated patient.
2.6.3 Pharmacoeconomic Model
The pharmacoeconomic model calculated the costs of treatment and relapse associated with each LAI dose regimen. Table 1 shows an overview of the transition probabilities, including the Cmin-dependent relapse probability for LAI estimated in the pharmacodynamic model. The transition probability from remission to relapse with SoC treatment was informed by the weighted average of probabilities of olanzapine, risperidone, quetiapine and ziprasidone [25]. The probability of transitioning from relapse to remission was derived from Medicaid data indicating a duration of first relapse of 4 weeks and was equal for all LAIs and SoC [26].
2.6.4 Discontinuation and Mortality
The discontinuation rate was informed by a medication discontinuation study using Truven MarketScan administrative claims data, which reported an annual all-cause discontinuation probability of 75.2% for patients with schizophrenia treated with AM [27]. The rate of 5.2% per cycle was assumed to also apply to patients treated with AL.
Mortality among people with schizophrenia is known to be higher than in the general population [28]. The age- and sex-dependent background mortality [29] was therefore adjusted with a standardized schizophrenia mortality ratio of 3.7 [30]. The mortality risk was assumed equal in all alive health states.
2.7 Cost Inputs
Wholesale average drug acquisition costs were sourced from the IBM Micromedex RED BOOK, and an overview of the costs is presented in Table 2 [31]. SoC treatment was assumed to consist of equal proportions of oral olanzapine, risperidone, quetiapine, and ziprasidone, in line with previous analyses [25]. Additional costs for the IM administration of AM and AL of $US14.31 per injection applied [32].
Disease management costs of patients in remission were included as a monthly monitoring visit relating to routine psychiatric and nonpsychiatric care, at a price of $US103.93 per visit [25]. The same source informed the costs associated with a relapse, reporting that 77.3% of patients experiencing relapse required hospitalization (Table 3) [25].
2.8 Analyses
To inform the patient-level simulation, the population was bootstrap-simulated until convergence of Cmin was reached (N = 2000), and distributions of Cmin and Cavg in steady state were generated as well as a pharmacokinetic profile over time for each LAI dose regimen. The number of relapses and the costs of LAIs, relapses, and SoC were presented per dose regimen as well as incremental results comparing dose regimens and the incremental cost per relapse avoided, using the dose regimen with the lowest mean number of relapses as the reference treatment.
2.8.1 Probabilistic Analysis
Using a probabilistic analysis (PA), we investigated the impact of parameter uncertainty in the pharmacodynamic and pharmacoeconomic models (the pharmacokinetic model already generates Cmin values under uncertainty in the base case). In line with guidelines, beta distributions were used for event rates, and lognormal distributions were fitted to costs and resource use estimates [34]. If standard errors were unavailable from the original source, these were assumed to be 10% of the mean estimate. During the PA, random values were drawn from all parameter distributions simultaneously and iteratively until convergence of outcomes was reached (N = 250). The outcomes of each iteration were recorded, and the distribution of outcomes was used to assess the overall uncertainty surrounding the costs and number of relapses of the dose regimens. Costs (by category) and numbers of relapses were presented per LAI dose regimen. CEACs showed the LAI dose regimens’ probabilities of cost effectiveness considering different WTP thresholds per relapse avoided.
2.8.2 Scenario Analyses
Key model settings and assumptions were evaluated in scenario analyses. These explored
-
a time horizon of 2 years (base-case time horizon 1 year),
-
pharmacodynamic model using Cmin as a continuous variable in the survival function (Cmin as dichotomous variable in the base case),
-
relapse costs 20% higher, and
-
relapse costs 20% lower.
2.9 Validation
To confirm the pharmacokinetic and pharmacodynamic models were correctly implemented in R, they were validated against the original models. Population pharmacokinetic profiles as well as Cmin, Cavg, and maximum plasma drug concentration (Cmax) were generated using the AM pharmacokinetic model in R and in NONMEM for eight sets of covariates, including and excluding parameter uncertainty (see ESM 2). The NONMEM model itself was validated against clinical data by assessing the difference between observed and predicted values in a cohort of patients [18]. The AL pharmacokinetic profiles were validated against published profiles [22]. The pharmacodynamic model in R was validated against the original SAS model by visually assessing Kaplan–Meier plots and comparing values at predefined landmarks (182 and 364 days). The SAS model itself was assessed against clinical data using goodness-of-fit statistics [24]. The face validity of the preexisting pharmacokinetic and pharmacodynamic models and their outcomes had been validated during the previous analyses and, for some models, during publication, and was not repeated. The computerized PK–PD–PE model underwent an assessment by an external modeler using extreme value testing to identify errors in terms of coding and calculations. The model results were externally validated with published US estimates of treatment and relapse costs per patient and costs per relapse avoided, real-world data, and estimates from pharmacoeconomic analyses. Differences between the PK–PD–PE model and existing publications (and potential reasons for the deviations) were investigated.
3 Results
3.1 Deterministic and Probabilistic Results
The distribution of patients with Cmin values above and below the 95 ng/mL threshold over time with each LAI dose regimen is presented in ESM 3. The probabilistic results show the mean number of relapses per patient was lowest with AM 400 mg and highest with AL 441 mg and 1064 mg q8wk (see Table 4). The total costs were lowest with AL 441 mg and highest with AL 882 mg q4wk and AM 400 mg. In general, dose regimens incurring higher LAI costs incurred lower relapse costs and vice versa. SoC treatment costs were equal for all dose regimens as discontinuation was assumed equal. When comparing the results of the dose regimen with the lowest number of relapses (AM 400 mg) against the other dose regimens, AM was dominant over AL 882 mg q4wk, which means more relapses were avoided against lower costs. The incremental cost per relapse avoided compared with the other treatments ranged from $US12,842 to 83,300.
The mean deterministic estimates of costs and relapses did not differ much compared with the probabilistic base case; see ESM 4. The conclusions based on average outcomes were unchanged.
Figure 2 shows the probabilistic incremental results, the number of relapses avoided, and incremental costs of AM 400 mg compared with the other dose regimens. Outcomes were visible in each quadrant of the cost-effectiveness plane, indicating uncertainty around the cost effectiveness of AM 400 mg.
Incremental probabilistic results: cost per relapse avoided of AM 400 mg q4wk compared with all other dose regimens, except AL 441 mg q4wk and AM 300 mg q4wk, which are only used in clinical practice when patients do not tolerate higher doses. AL aripiprazole lauroxil, AM aripiprazole monohydrate, qxwk every × weeks
The CEAC (Fig. 3) indicates that, for WTP thresholds up to $US30,000 per relapse avoided, AL 1064 mg q8wk had the largest probability of cost effectiveness, followed by AM 400 mg. For a WTP of $US30,000 or higher, AM 400 mg had the largest probability of cost effectiveness (35%), increasing to 41% at a WTP of $US50,000 and to 54% at a WTP of $US200,000. For WTP above $US65,000, AL 662 mg had the second-largest cost-effectiveness probability. AL 1064 mg q6wk and 882 mg q4wk had low probabilities throughout the entire WTP range, whereas AL 882 mg q6wk reached cost-effectiveness probabilities of > 20% at a WTP threshold of $US50,000–65,000.
3.2 Scenario Analyses
Detailed results of all scenario analyses can be found in ESM 4. Increasing the time horizon to 2 years increased the total costs driven by increased SoC treatment costs. The number of relapses avoided of AM 400 mg versus other dose regimens increased, as did the cost per relapse avoided. Treating Cmin as a continuous covariable decreased the number of relapses of all dose regimens as well as the total costs. This resulted in increased incremental costs per relapse avoided of AM 400 mg versus other dose regimens. Increasing the relapse costs by 20% decreased the incremental cost per relapse avoided of AM 400 mg versus other dose regimens by approximately $US5000 in each comparison; a 20% increase caused a $US3000 increase in the incremental cost per relapse avoided.
3.3 Validation
The validation of the AM pharmacokinetic model indicated no significant differences in the NONMEM and R models in (deterministic) concentration profiles or in simulated steady-state Cmin, Cavg, and Cmax under uncertainty (Student’s t test p values > 0.05). The median central concentrations generated by the AL pharmacokinetic model (including parameter uncertainty) were comparable with published data [22], and the profiles can be inspected in Fig. 1 in ESM 2. The replicated pharmacodynamic model in R showed overlapping survival curves and equal values as the SAS model at predefined landmarks (see Fig. 2 in ESM 2).
4 Discussion
To enable the pharmacoeconomic assessment of schizophrenia treatment with different aripiprazole LAI dose regimens in the absence of RCT data, a PK–PD–PE or PMPE model utilizing pharmacokinetic and pharmacodynamic evidence was developed. The model used two dose regimens of AM and six dose regimens of AL to compare their number of relapses and the treatment and relapse costs over a time horizon of 1 year. The estimated number of relapses was lowest for AM 400 mg, which incurred the lowest relapse costs and the second-highest LAI costs. The incremental cost per relapse avoided ranged from $US12,842 compared with AL 1064 mg to $US83,300 compared with AM 300 mg. AL 882 mg q4wk was dominated by AM 400 mg. For a WTP of ≥$US30,000 per relapse, AM 400 mg had the largest probability of cost effectiveness (35% at $US30,000, 41% at $US50,000, 54% at $US200,000), indicating the results were subject to uncertainty. The results were most sensitive to the cost per relapse.
Previous cost-effectiveness models for schizophrenia with LAIs and oral treatments in the USA estimated similar treatment costs, numbers of relapses, and costs per relapse avoided [25, 35,36,37,38] (see ESM 5). The PK–PD–PE model estimated 0.224–0.317 (probabilistic) relapses with AM 400 mg, which aligned with previously reported ranges of 0.181–0.277 [38] and 0.20–0.55 [35] and stayed below the range of 0.363–0.600 [25] in a comparison of oral treatments. Likewise, the estimated total treatment costs of $US18,123–25,927 (probabilistic) aligned with those from other studies. The number of relapses avoided with the most effective treatment relative to comparators in the PK–PD–PE model was somewhat lower than in two previous studies [25, 38]. Different treatment discontinuation assumptions may partly explain this result. The only reported cost per relapse avoided was at the lower end of the range of the PK–PD–PE model [38]. Overall, the validation confirmed that the PK–PD–PE model allowed for an indirect comparison of two LAI formulations with different pharmacokinetic profiles in the absence of clinical data.
Although parameter uncertainty was assessed in the probabilistic sensitivity analysis, and assumptions were tested in scenario analyses, some structural uncertainty remained. The Cmin levels of the LAIs were modeled using two pharmacokinetic models that used slightly different structures. These differences, rather than the differences in the pharmacokinetic characteristics of the biological agents, may bias the Cmin levels to an unknown degree. The pharmacodynamic model generated the occurrence of relapses as a function of Cmin levels and did not consider additional patient characteristics. This simplifying assumption might not reflect the impact of other patient characteristics on relapse. The relapse hazard was modeled within a binary framework because exposure–response analysis suggested that the risk of impending relapse increases as the aripiprazole Cmin decreases below a cut-off point of 95 ng/mL. This cut-off point is consistent with the lower boundary of the established therapeutic window for aripiprazole [14]. The relapse probabilities, and hence the model results, would be sensitive to changes in this cut-off point, but we were unable to explore this in the present study as we used an existing pharmacodynamic model [24]. Evidence of a positive relationship between aripiprazole levels and the probability of side effects is limited [39]; however, the current approach may underestimate the potential disadvantage of higher dosed regimens because of increased adverse events. The risk of mortality was assumed equal for patients in remission and relapsed patients, as detailed evidence was not available. Expert opinion indicates that mortality risk is likely higher during relapse than during remission. This pragmatic modeling approach omits potential survival benefits achieved by treatments reducing the frequency of relapse. Considering the 1-year time horizon of the analysis, the impact on the results is likely minimal. The 1-year time horizon, corresponding to other pharmacoeconomic analyses, might not completely capture the impact of LAI treatment and potential future impacts of dosing and drug concentration on relapses. However, the scenario analysis using a 2-year time horizon had minimal impact because only 6% of patients remained on treatment at 2 years.
The successful validation and the flexibility of the novel PMPE or PK–PD–PE framework suggests that application of this strategy might be feasible in other therapies and disease areas with similar data restrictions. This is especially relevant considering model-informed drug development (MIDD) programs such as the FDA pilot program [40]. Applying pharmacoeconomic components in MIDD could facilitate early economic evaluations, but we demonstrated that the PMPE [16, 17] framework also enables postmarketing pharmacoeconomic evaluations of drug formulations that access the market based on MIDD. However, modeling findings should still be supplemented, or even supplanted, by clinical trial evidence when available [16]. In this case, where aripiprazole LAI formulations are marketed in the USA and phase III RCT evidence may not become available for all approved dose regimens, future real-world evidence could yield inputs for adherence, discontinuation, mortality, and (relapse) treatment costs in practice. For the present PK–PD–PE analysis, the deterministic, probabilistic, and scenario analysis consistently indicated, with a high degree of uncertainty, that AM 400 mg is the most cost-effective LAI dose regimen for schizophrenia treatment.
The findings of the analysis may have implications for clinical practice of schizophrenia treatment. Higher LAI doses, especially AL 882 mg q4wk and AL 1064 mg q8wk, are frequently used in current clinical practice [41]. An understanding of both the clinical and the economic consequences of different LAI dose regimens may help physicians and US payers make informed decisions on dose ranges of LAIs that offer reduced relapse rates at reduced costs.
5 Conclusion
The PK–PD–PE analysis of different aripiprazole LAI dose regimens for the treatment of schizophrenia highlighted the robustness of the novel PMPE framework used. The analysis indicated that the lowest number of relapses and highest cost-effectiveness probability were obtained with AM 400 mg. The estimates obtained from this modeling exercise are subject to uncertainty and rely on several assumptions for operational purposes. The analysis demonstrated how PMPE methods may be used to inform clinical and payer decisions in the absence of clinical trial data in a postmarketing setting.
References
R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria; 2020. http://www.R-project.org/.
Wang W, Hallow KM, James DA. A tutorial on RxODE: simulating differential equation pharmacometric models in R. CPT Pharmacometr Syst Pharmacol. 2016. https://doi.org/10.1002/psp4.12052.
Lieberman JA, Perkins D, Belger A, et al. The early stages of schizophrenia: speculations on pathogenesis, pathophysiology, and therapeutic approaches. Biol Psychiatry. 2001. https://doi.org/10.1016/s0006-3223(01)01303-8.
National Collaborating Centre for Mental Health. Schizophrenia: core interventions in the treatment and management of schizophrenia in primary and secondary care (Update). Leicester (UK): British Psychological Society. Copyright©. 2009.
Agid O, Foussias G, Remington G. Long-acting injectable antipsychotics in the treatment of schizophrenia: their role in relapse prevention. Expert Opin Pharmacother. 2010. https://doi.org/10.1517/14656566.2010.499125.
Biagi E, Capuzzi E, Colmegna F, et al. Long-acting injectable antipsychotics in schizophrenia: literature review and practical perspective, with a focus on aripiprazole once-monthly. Adv Ther. 2017. https://doi.org/10.1007/s12325-017-0507-x.
Melkote R, Singh A, Vermeulen A, et al. Relationship between antipsychotic blood levels and treatment failure during the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) study. Schizophr Res. 2018. https://doi.org/10.1016/j.schres.2018.05.028.
McCutcheon R, Beck K, D’Ambrosio E, et al. Antipsychotic plasma levels in the assessment of poor treatment response in schizophrenia. Acta Psychiatr Scand. 2018. https://doi.org/10.1111/acps.12825.
Keith SJ, Kane JM. Partial compliance and patient consequences in schizophrenia: our patients can do better. J Clin Psychiatry. 2003. https://doi.org/10.4088/jcp.v64n1105.
Llorca PM. Partial compliance in schizophrenia and the impact on patient outcomes. Psychiatry Res. 2008. https://doi.org/10.1016/j.psychres.2007.07.012.
van Os J, Kapur S. Schizophrenia. Lancet. 2009. https://doi.org/10.1016/S0140-6736(09)60995-8.
Otsuka Pharmaceutical Company. Prescribing information abilify maintena. 2016.
Alkermes. Prescribing information Aristada. 2018.
Salzman PM, Raoufinia A, Legacy S, et al. Plasma concentrations and dosing of 2 long-acting injectable formulations of aripiprazole. Neuropsychiatr Dis Treat. 2017. https://doi.org/10.2147/NDT.S133433.
Li L, Tran D, Zhu H, et al. Use of model-informed drug development to streamline development of long-acting products: can these successes be translated to long-acting hormonal contraceptives? Annu Rev Pharmacol Toxicol. 2021. https://doi.org/10.1146/annurev-pharmtox-031120-015212.
Hill-McManus D, Marshall S, Liu J, et al. Linked pharmacometric-pharmacoeconomic modeling and simulation in clinical drug development. Clin Pharmacol Ther. 2020. https://doi.org/10.1002/cpt.2051.
Srinivasan M, White A, Chaturvedula A, et al. Incorporating pharmacometrics into pharmacoeconomic models: applications from drug development. Pharmacoeconomics. 2020. https://doi.org/10.1007/s40273-020-00944-0.
Center for Drug Evaluation and Research. Clinical pharmacology and biopharmaceutics review of aripiprazole lauroxil (NDA 207533). 2015. https://www.accessdata.fda.gov/drugsatfda_docs/nda/2015/207533Orig1s000ClinPharmR.pdf Accessed 15 Jul 2021.
Institute for Cost-Effectiveness Research. ICER’s reference case for economic evaluations: principles and rationale. 2018. https://icer-review.org/wp-content/uploads/2018/07/ICER_Reference_Case_July-2018.pdf Accessed 3 Mar 2021.
Nasrallah HA, Aquila R, Du Y, et al. Long-term safety and tolerability of aripiprazole lauroxil in patients with schizophrenia. CNS Spectr. 2019. https://doi.org/10.1017/S1092852918001104.
Potkin SG, Risinger R, Du Y, et al. Efficacy and safety of aripiprazole lauroxil in schizophrenic patients presenting with severe psychotic symptoms during an acute exacerbation. Schizophr Res. 2017. https://doi.org/10.1016/j.schres.2017.03.003.
Hard ML, Mills RJ, Sadler BM, et al. Pharmacokinetic profile of a 2-month dose regimen of aripiprazole lauroxil: a phase I study and a population pharmacokinetic model. CNS Drugs. 2017. https://doi.org/10.1007/s40263-017-0447-7.
SAS Institute Inc. Cary, NC, USA. 2021.
Otsuka Pharmaceutical Development and Commercialization Inc. Technical report: exposure-response analyses of impending relapse in pivotal phase 3 safety and efficacy trials of aripiprazole IM depot (Trial 31-07-246 And Trial 31-07-247). 2014.
Aigbogun MS, Liu S, Kamat SA, et al. Relapse prevention: a cost-effectiveness analysis of brexpiprazole treatment in adult patients with schizophrenia in the USA. Clinicoecon Outcomes Res. 2018. https://doi.org/10.2147/CEOR.S160252.
Lafeuille MH, Gravel J, Lefebvre P, et al. Patterns of relapse and associated cost burden in schizophrenia patients receiving atypical antipsychotics. J Med Econ. 2013. https://doi.org/10.3111/13696998.2013.841705.
Yan T, Greene M, Chang E, et al. Medication adherence and discontinuation of aripiprazole once-monthly 400 mg (AOM 400) versus oral antipsychotics in patients with schizophrenia or bipolar i disorder: a real-world study using US claims data. Adv Ther. 2018. https://doi.org/10.1007/s12325-018-0785-y.
Brown S, Kim M, Mitchell C, et al. Twenty-five year mortality of a community cohort with schizophrenia. Br J Psychiatry. 2010. https://doi.org/10.1192/bjp.bp.109.067512.
Arias E, Xu JQ, Kochanek KD. United States life tables. 2016. National vital statistics reports. Hyattsville, MD: National Center for Health Statistics; 2019.
Olfson M, Gerhard T, Huang C, et al. Premature mortality among adults with schizophrenia in the United States. JAMA Psychiat. 2015. https://doi.org/10.1001/jamapsychiatry.2015.1737.
IBM Micromedex. Red Book. 2021.
Centers for Medicaid and Medicare Services. Physician fee schedule. 2021. https://www.cms.gov/Medicare/Medicare-Fee-for-Service-Payment/PhysicianFeeSched/index.html Accessed 3 Mar 2021.
Organisation for economic co-operation and development. harmonized consumer price indices by COICOP by country. 2021. https://stats.oecd.org/ Accessed 4 Mar 2021.
Briggs AH, Weinstein MC, Fenwick EA, et al. Model parameter estimation and uncertainty analysis: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group-6. Med Decis Making. 2012. https://doi.org/10.1177/0272989X12458348.
Ascher-Svanum H, Furiak NM, Lawson AH, et al. Cost-effectiveness of several atypical antipsychotics in orally disintegrating tablets compared with standard oral tablets in the treatment of schizophrenia in the United States. J Med Econ. 2012. https://doi.org/10.3111/13696998.2012.662923.
Ascher-Svanum H, Stensland MD, Peng X, et al. Cost-effectiveness of olanzapine vs aripiprazole in the treatment of schizophrenia. Curr Med Res Opin. 2011. https://doi.org/10.1185/03007995.2010.537594.
Smith KJ, Baik SH, Reynolds CF, et al. Cost-effectiveness of Medicare drug plans in schizophrenia and bipolar disorder. Am J Manag Care. 2013;19(2):e55-63.
Citrome L, Kamat SA, Sapin C, et al. Cost-effectiveness of aripiprazole once-monthly compared with paliperidone palmitate once-monthly injectable for the treatment of schizophrenia in the United States. J Med Econ. 2014. https://doi.org/10.3111/13696998.2014.917089.
Auby P, Saha A, Ali M, et al. Safety and tolerability of aripiprazole at doses higher than 30 mg. Eur Neuropsychopharmacol. 2002. https://doi.org/10.1016/s0924-977x(02)80406-0.
US Food & Drug Administration. Model-informed drug development pilot program. 2021. https://www.fda.gov/drugs/development-resources/model-informed-drug-development-pilot-program.
Otsuka Pharmaceutical Company. Aristada 882 and 1064 dose frequency breakdown (Data on File). 2019.
Acknowledgements
The authors thank Svenja Petersohn (employee of OPEN Health) for her medical writing assistance and editorial support for this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
This study was funded by a grant from Otsuka.
Conflict of interest
MAP, NH, CB, and CK are employees of OPEN Health and were paid consultants to Otsuka with regard to the development of this manuscript. HW, RAD, XW, and SM are employees of Otsuka. MAP, NH, CB, CK, HW, RAD, XW, and SM have no conflicts of interest that are directly relevant to the content of this article.
Ethics approval
Not applicable.
Consent
Not applicable.
Availability of data and material
Input data for the generation of the results are available in this article and its appendices.
Code availability
The presented model was built in R version 4.0.2, making use of the RxODE R package. R and RxODE are openly available and licensed under GPL-2/3. In addition, custom R code was developed by the authors.
Author contributions
All authors adhered to the International Committee of Medical Journal Editors authorship criteria. MAP was the leading author who designed the pharmacoeconomic model and conducted the analyses together with CK. NH, CB, HW, RAD, XW, and SM contributed to the study design and interpretation of analysis. All authors reviewed the subsequent drafts and provided comments and the final approval of the manuscript for submission.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Piena, M.A., Houwing, N., Kraan, C.W. et al. An Integrated Pharmacokinetic–Pharmacodynamic–Pharmacoeconomic Modeling Method to Evaluate Treatments for Adults with Schizophrenia. PharmacoEconomics 40, 121–131 (2022). https://doi.org/10.1007/s40273-021-01077-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40273-021-01077-8