1 Introduction

Environmental change and global sustainability are posing new challenges for engineers in the transportation industry to develop the next generation of products. For instance, sustainability in the maritime sector requires the effective use of high-strength steels in the large welded structures. In combination with new structural topologies, the weight of cruise ships can be reduced considerably [1, 2]. The limiting factor of higher strength materials is their sensitivity to defects induced in the manufacturing process. Therefore, e.g. the cutting and welding processes need to be optimised for the new steel grades. Results have shown that by using high-quality manufacturing, the load carrying capacity of high-strength steels can be significantly higher compared to conventional steels and to considerably exceed the design values set by classification society guidelines [2,3,4,5]. A fundamental aspect is understanding how the material properties change during the manufacturing process and discovering the underlying microstructural characteristics that explain these changes.

In general, the mechanical properties of metallic materials have been shown to correlate with the microstructural dimensions, most commonly with the average grain size according to the Hall–Petch relationship [6, 7]:

$$\sigma=\sigma_0+{kd}^{-1/2},$$
(1)

where \({\sigma }_{0}\) is the lattice friction stress required to move individual dislocations, k is a material-dependent constant known as the Hall–Petch slope, and d is the average grain size [8]. The Hall–Petch relationship applies to a large variety of materials and material properties, such as hardness, stress–strain properties, and fatigue [9,10,11,12,13,14,15]. However, in addition to the average grain size, other material-specific factors such as differences in phase volume fractions and grain size distribution need to be considered for ferritic steel weld metals in order to predict material properties in a general case.

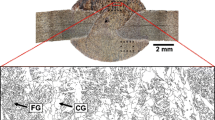
Broad grain size dispersions are often observed for ferritic weld metals, and it is of particular interest since it has been shown to influence the mechanical properties [16,17,18,19]. Improved grain size measurement methods are thus required to enhance the understanding between grain size dispersion and mechanical properties of welded joints [19]. Welds are an extreme case of heterogeneity since it is present both in macroscopic scale across the joint and in microscopic scale within a single zone; see Fig. 1.

Fig. 1
figure 1

Spatial grain size measurement for base metal and an arc-welded joint, showing the variation of grain size dispersion across the joint and within a single zone. Grain size is shown using the Hall–Petch parameter d−0.5 (µm−0.5), and thus, larger values indicate smaller grain size or higher strength. Modified after [19]

Full size image

The grain size characterisation of ferritic steel weld metals was studied by Lehto et al. [18, 19]. The grain size measurements revealed that welds exhibit a variety of grain size dispersions that are noticeably broader than those of ferritic base metals. The volume-weighted grain size measurement was utilised to capture the influence of grain size dispersion. It was shown that the Hall–Petch relationship’s dependence on grain size dispersion is eliminated when then volume-weighted average grain size (dv) is used:

$$\sigma ={\sigma }_{0}+{{kd}_{v}}^{-1/2}={\sigma }_{0}+{kd}^{-\frac{1}{2}}(1+f\frac{\Delta d}{d})$$
(2)

where \(f\) is a constant describing the relation between average and volume-weighted average grain size and \(\Delta d/d\) is the relative grain size dispersion. When samples with similar grain size dispersion are compared, both the original (1) and modified (2) Hall–Petch relationship may be used. However, this is rarely the case for ferritic weld metals, and the modified Hall–Petch relationship (2) has been shown to improve the prediction of mechanical properties [18]. This comparison assumes that the phase volume fractions of the compared materials are similar. In addition, Eq. 2 does not consider the influence of grain sub-structure, the generation of which is affected by the heat cycle during, e.g. welding or cutting.

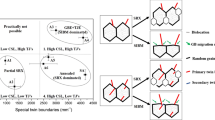
To better understand the strength properties of the ferritic weld metals, the grain sub-structures must be studied. The sub-structural boundaries and deformation patterns in polycrystals are material dependent, affected, e.g. by the structure of the crystal lattice, chemical composition, magnitude of strain, strain rate, and temperature [20, 21]. The cell-forming mechanism is commonly observed in many materials with different crystal structures, for example in copper (FCC) [22], aluminium (FCC) [23], magnesium alloys (HCP) [24], and iron (BCC and FCC) [20, 25]. In the cell-forming process, the lattice dislocation re-arrange to minimise the local energy state, forming dense dislocation walls (DDWs), dislocation tangles (DTs), sub-grain boundaries (SGBs), and eventually new grain boundaries (GBs) inside the grains with severe strains [20]; see Fig. 2. While conventionally transmission electron microscopy (TEM) is required to study the (deformation-induced) dislocation sub-structures, recently Lehto [26] developed the adaptive domain misorientation approach that can provide information of these features using conventional EBSD.

Fig. 2
figure 2

Schematic representation showing the evolution of grain’s sub-structure during plastic deformation for a cell-forming material, starting from the formation of dense dislocation walls and dislocation cells, followed by sub-grain boundaries, and ultimately leading to the formation of new grain boundaries [26]

Full size image

The aim of the current work is to apply advanced EBSD analysis tools for the characterisation of ferritic steel weld metals. As the first task, the previously published grain size measurement methods [18, 19, 27] are implemented to work directly with EBSD datasets. Because the solidification of the microstructure is highly dependent on the heat cycle and the utilised welding process, differences are also expected to arise in a scale smaller than the grain structure. Three distinctly different ferritic steel weld metals are included in the test series to study the formation of dislocation sub-structures during the welding process. The results show differences in the dislocation sub-structures and highlight the need for more detailed microstructural characterisation for the prediction of mechanical properties. The developed tools are provided as open access [27, 28], together with the example datasets used in the current study [29].

2 Methods

2.1 Weld samples

Samples manufactured using conventional arc (CV), laser (LA), and laser-hybrid (HY) welding were investigated to study the influence of welding process on the size of grain and sub-grain sub-structure. The weld metals represent complex microstructures with various grain size dispersions and different heat cycles leading to different phase volume fractions. Table 1 lists specimen nomenclature with the corresponding joint type, welding method, and constituent volume fractions as classified by [30], and the base metal properties are listed in Table 2. For convenience, the microstructures are referred to using their welding method abbreviations. The edges of the plates were prepared using plasma cutting and grinding (CV.3), laser cutting (HY.1), and milling (LA.1). The laser weld has the highest hardness, followed by laser-hybrid and arc welding. Details of the hardness measurements are available in Ref. [18].

Table 1 Test specimen nomenclature and the corresponding joint types, welding methods, and material phase volume fractions
Full size table
Table 2 Mechanical properties and chemical composition of base materials [18]
Full size table

Transverse cuts in relation to the welding direction were used for the test specimens. The cut sections were mounted in an electrically conductive resin and grinded using P180-P4000 grit abrasive papers, followed by polishing with 3 µm, 1 µm, and 0.25 µm diamond paste and polishing with colloidal silica in a vibratory polisher; see Fig. 3 for cross-sections and measurement locations. For optical micrographs, the samples were etched with 2% Nital. The investigations were carried out for weld metal regions highlighted by the white rectangles in Fig. 3.

Fig. 3
figure 3

Macro-sections of the weld samples. White rectangles show the location for hardness measurements and EBSD analysis

Full size image

2.2 Microstructure characterisation

The microstructures were characterised using electron backscatter diffraction (EBSD). EBSD analyses were carried out at the location of hardness indentations or in close proximity where the microstructure is similar. A Zeiss Ultra 55 field emission scanning electron microscope equipped with a Nordlys F + camera and Channel 5 software from Oxford Instruments was used for the EBSD analyses. The EBSD analyses were performed with a step size of 0.1 µm at a magnification of 3000 × and a grain boundary misorientation criterion of 10°. The acceleration voltage was 20 kV, and the working distance was 19.5 mm. The indexing rate of the EBSD maps varied between 88 and 93%, depending on grain size and material phase.

The EBSD data was post-processed and analysed using the open-source toolbox MTEX version 5.6 [31, 32]. The MTEX toolbox was operated using Matlab version R2021a. The orientation data was post-processed with the half-quadratic filter developed by Bergmann et al. [33] to reduce measurement noise and assign orientations to the non-indexed points. The half-quadratic minimisation method is designed to restore images with noise and missing data, and it is particularly efficient for de-noising EBSD data. The half-quadratic filter effectively removes the spatially independent noise from the orientation measurement data while maintaining the sharp gradients at the grain boundaries and sub-structural boundaries. Its performance is compared to other conventional de-noising options, such as the mean, median, and Kuwahara filters in Ref [34]. The used de-noising parameters are shown in Table 3. The de-noised orientation maps with > 10° grain boundaries are shown in Fig. 4. Example EBSD datasets of the three welds used in this publication are available as open access from Ref. [29].

Table 3 Parameters used for EBSD data de-noising with the half-quadratic filtering in MTEX version 5.6 [26]
Full size table
Fig. 4
figure 4

Forescatter detector images (FSD) and orientation maps (IPF-Z) for the three samples. Grain boundaries (> 10°) are overlaid on black for the orientation maps

Full size image

2.3 Grain size measurements

The average grain size was measured using the ASTM E1382 [35] linear intercept length method in four evenly spaced directions (0°, 45°, 90°, 135°), which is hereafter referred to as the line-sampled intercept length method. The volume-weighted average grain size was measured using the point-sampled intercept length method [36, 37]. For the point-sampled linear intercept length method, a measurement value is associated with each data point, and thus, the averaged value of all data points is area-weighted, or volume-weighted according to the principles of stereology [18, 36, 37]. The intercept length method is utilised in this study to represent the length of the slip planes for ferritic steel weld metals, and it is chosen over the grain-based metrics (see, e.g. ASTM E2627 [38]) due to its robustness. The main challenge with grain-based metrics is their sensitivity to small discontinuities in the grain boundaries, which are often observed in ferritic weld metals. Should there be just one data point at the grain boundary which does not meet the set misorientation criterion, for example, 10°, will cause two (or more) neighbouring grains to be merged together; see Fig. 5A–B. In addition, the calculation of an equivalent diameter assumes a circular shape for the grains, while in many weld metals, the grains can be highly elongated or have a complex grain boundary shape; see Fig. 5B–C. The linear intercept method is much more tolerant to these issues, as only a small fraction of measurements within the specific grain will be affected by the missing grain boundary; see Fig. 5D. Additionally, the linear intercept method better represents the actual variation in the length of the slip planes, i.e. the free path between obstacles for dislocation motion; see Fig. 5E. As shown in Fig. 5C, the equivalent circle diameter is a poor representation of the actual length of slip planes and does not consider the variability of slip plane’s length for complex grain shapes observed in ferritic weld metals. For further details of the intercept length methods, refer to the previous publications and Matlab implementation by Lehto et al. [18, 19]. For comparison of intercept length and grain-based metrics, see the work of Mingard et al. [39,40,41].

Fig. 5
figure 5

Grain size measurement example for the bainitic/martensitic microstructure of LA-1. A Orientation map with the merged grains highlighted by the white arrows and outline, and the region of the selected grain showing: B the complex grain morphology, with red colour shows the internal ‘leaking’ grain boundaries, C an area equivalent circle and its diameter, D point-sampled linear intercept measurement showing the size distribution within the grain, and E distribution and the average value of linear intercept length

Full size image

The dispersions measured with the line-sampled linear intercept method were characterised with the relative grain size dispersion [18], modified from Berbenni et al. [42]:

$$\frac{\Delta d}{d}=\frac{d_{\mathrm{max}}-{d}_{\mathrm{min}}}{d}=\frac{P_{99\%}-{P}_{1\%}}{d},$$
(3)

where the maximum and minimum grain sizes are replaced by the 99% and 1% probability level grain sizes, respectively. This minimises measurement uncertainty, which is inherently most prominent at the extremities of the dispersion due to the finite number of measurements. This metric represents the variability of grain size, with smaller values indicating a more uniform grain size.

The previous implementation, available at Ref. [27], utilises the image processing toolbox available in Matlab. The input data is an image file of the grain boundary map in a binary format (black-white), extracted either from optical images or EBSD data. In this work, the methods are implemented to work directly with EBSD data using the open-source toolbox MTEX version 5.6 [31, 32]. The implementation utilises the intersect feature of MTEX to detect the locations of grain boundaries on pre-defined measurement lines. In the current study, the grain boundaries were defined to be located between data points where the misorientation is larger than 10° to represent the high-angle boundaries typically quoted as effective barriers for dislocation motion; see, e.g. [43]. It should be noted that a bugfix (intersect.m) is required for MTEX versions prior to 5.6; see [44]; otherwise measurement may bleed through grain boundaries. The line-sampled and point-sampled intercept length are measured simultaneously at one-pixel intervals for horizontal, vertical, and ± 45° measurement directions. The average value of the four measurement directions is associated as the grain size at each data point of the EBSD map to generate spatial information [19]. Sampling all data points yields the same results as sampling random points, since both will weigh the measurement according to the surface area fraction of grain size which has a relationship to the volume fraction of the grains. Thus, the random sampling approach initially used by Gundersen and Jensen [36, 37] in the point-sampled method is not required, and a grain size value can be associated with every data point of the EBSD measurement. The conventional average grain size and the relative grain size dispersion are measured using the line-sampled procedure. The spacing between horizontal and vertical measurement lines is 7 data points, and 10 data points for the 45° measurements to equally sample all four directions. Only one grain size value is recorded between the two grain boundaries, and thus, no detailed spatial information is generated; see [18, 19] for further details.

The EBSD implementation removes the workload and uncertainties related to extracting grain boundary images and the calibration of scaling for the images. The measurement speed for the point-sampled approach is increased by assigning the grain size of a single measurement line to all data points belonging to the intersect line. In addition to the efficiency of MTEX, computational efficiency is increased by utilising parallel computing. A typical analysis takes from some tens of seconds to a few minutes, depending on EBSD map size and density of grain boundaries. The EBSD-based grain size measurement code is available at references [27, 28].

The use of EBSD data enables a high degree of flexibility for the definition of the grain boundaries. In addition to the complete grains (grains.boundary), the discontinuous grain boundary segments (grains.innerBoundary) were considered for the analysis. Welds often have orientation gradients, causing small segments of the grain boundaries to be missing between adjacent grains; see [45] for details in the MTEX definitions. In the current study, the misorientation threshold for both boundary types is the same at 10°. The incomplete grain boundary segments can be excluded by setting include_innerGB = false in the measurement code. Starting with MTEX version 5.5, the inner boundaries can also be defined with a misorientation angle lower than grain boundaries; see [46] for details.

2.4 Characterisation of grain sub-structures

The grain sub-structures for the three weld metal samples were analysed using the adaptive domain misorientation approach [26], available as open-source at Refs. [47, 48]. The domain misorientation approach is tailored for detecting the changes in lattice curvature induced by the cell-forming dislocation mediated plastic deformation process, shown schematically in Fig. 2. The development of this measurement approach is reasoned by the fact that the cell-forming mechanism is observed in many metallic materials with different crystal structures, for example, in copper (FCC) [22], aluminium (FCC) [23], magnesium alloys (HCP) [24], and iron (BCC and FCC) [20, 25]. While the conventional kernel misorientation approach measures the orientation gradient to the nearest neighbours of each data point, the domain misorientation adapts the measurement area to the size of the sub-structures, shown schematically in Fig. 6. This enables stochastic analysis of local misorientation to be carried out within individual sub-grains and dislocation cells and to resolve the differences in grain sub-structures for the ferritic steel weld metals. The capability is founded on measuring orientation gradients over larger zones, for example, in the sub-grain boundary region with a thickness of 100–500 nm, as opposed to the point-to-point gradient determination with kernel misorientation. This makes the approach more tolerant to the angular measurement noise of conventional EBSD. Furthermore, the approach enables the size dispersion of the sub-structures to be measured. The principle of weighting is the same as for the point-sampled linear intercept method, i.e. a size metric is associated with each data point, and then by averaging all data points, an area-weighting (or volume-weighting based on the principles of stereology) is automatically applied. For domain misorientation approach, the size of the measurement area is converted from the number of data points to ‘an equivalent square’ base dimension so it can be compared to the kernel size set by the operator. This approach has been tested for the size distribution measurement of dislocation cells, showing a very close match with the result obtained using the point-sampled intercept length method [49].

Fig. 6
figure 6

Schematic illustration of the size of measurement area for kernel misorientation and domain misorientation. For the latter, the measurement area is denoted ‘deformation domain’ and is shown for A dense dislocation walls (ΔθDDW = 0.5°) and B dislocation cells (ΔθDDW = 0.5°). The shaded green area is the deformation domain within the misorientation value, and red shading is an excluded area. Kernel misorientation schematic modified after [50], and original grain sub-structure TEM image by Klemm [51] after [52]

Full size image

In the current work, the domain misorientation approach was used to study the presence of grain sub-structure induced by the solidification of the weld metals. Based on the orientation maps in Fig. 4, no apparent orientation gradients are observed for the arc and laser-hybrid welds. Therefore, the sub-structure is expected to be minor, with only dense dislocation walls and dislocation cells present, as shown schematically in Fig. 2. The study is focused on measuring the differences in the dislocation cell structure, and thus, the criterion ΔθDDW = 0.5° is used for the domain misorientation approach. The initial (maximum) kernel size is defined as 60 nearest neighbours (12.1 × 12.1 µm) to cover the largest grains. The analysis is carried out for 6–14 EBSD scans for the three welds, with an individual scan covering an area of 124.5 µm × 93.4 µm.

3 Results and discussion

3.1 Grain size dispersion and the relationship between grain size parameters

The measured average grain sizes for the three weld metals are shown in Fig. 7. The figure also includes a large number of weld metal EBSD maps (n = 59) from different arc, laser, and laser-hybrid welds and presents previous image-based analyses [18], including two different S355 base metals for comparison. The ferritic steel weld metals have smaller average grain sizes than the S355 base metals, and the volume-weighted average grain sizes are proportionally larger for the weld metals. On average, the laser-hybrid weld metal has the smallest volume-weighted average grain size, followed by the arc and laser weld metals. However, there is considerable spatial grain size variation due to the spatial variation of the phase volume fractions. This applies especially to the laser-hybrid weld metal as the volume fraction of the fine-grained acicular ferrite and coarse-grained primary ferrite varies from field to field, as shown in the inset of Fig. 7 and in Fig. 8. This highlights the fact that a single EBSD scan must contain a sufficient number of grains [39, 41] and that the measured surface area needs to cover the macroscopic variation. Therefore, the grain size parameters should be averaged over all EBSD scans and presented with a variation metric such as the 95% confidence interval. In general, the grain size parameters measured with the EBSD approach show good correspondence with the previous image-based analyses reported in detail in [18]. Few of the earlier analyses are based on optical images (S355 base metal, annealed weld metal), and no EBSD data exists for those specimens. Some deviations are observed for the average grain sizes, arising from the fact that the grain boundaries were thicker in the image-based analysis. Thus, as the thickness of grain boundaries is reduced from 2 to 3 pixels to be a line precisely in the middle of two data points, the small grains can be sampled more reliably. This slightly decreases the measured average grain size values.

Fig. 7
figure 7

The average and volume-weighted average grain sizes for ferritic steel weld metals and S355 base metals. The filled markers show the results obtained with the EBSD-based implementation, while the magenta crosses show the data with image-based implementation published in [18]. The inset shows the region highlighted by the red dashed rectangle for the three welds analysed in this work, with the leaders indicating the orientation maps shown in Fig. 4

Full size image
Fig. 8
figure 8

Spatial distribution of grain size for the laser-hybrid weld consisting of primary ferrite (coarse grains) and acicular ferrite (fine grains). Grain size is shown using the Hall–Petch parameter d−0.5 (µm−0.5), and thus, larger values indicate smaller grain size or higher strength

Full size image

Another essential aspect for grain size characterisation of welds is to measure the dispersion of grain size. The dispersion measured by the EBSD-based implementation is compared to the ratio of average grain size parameters, dv−0.5/d−0.5, in Fig. 9. It can be observed, as already visually indicated by Fig. 8, that the grain size dispersion has a considerable macroscopic variation for the laser-hybrid weld metal consisting of a mixture of primary and acicular ferrite. The same applies to the arc weld, with both narrow and broad dispersions observed. The range of dispersion observed is the smallest for the laser weld metal consisting of bainite and martensite.

Fig. 9
figure 9

The relationship between grain size parameters measured using the line-sampled intercept length method (d, Δd/d) and the point-sampled intercept length method (dv). The filled markers show the results obtained with the EBSD-based implementation, while the magenta crosses show the data with image-based implementation published in [18]. The dashed black and red lines are the 95% confidence and prediction bounds for the image-based analysis

Full size image

Previous research by Lehto et al. [18] has shown that the average and volume-weighted average grain sizes have a relationship to the grain size dispersion. This relationship makes it possible to estimate the volume-weighted grain size based on conventional grain size measurement data typically reported in scientific publications. The overall relationship between the grain size parameters is approximately the same as in previous image-based analyses [18]; see Fig. 9. The relative grain size dispersion values (Δd/d) are slightly larger with the EBSD-based analysis, owing to the reduction of grain boundary thickness, leading to a more accurate measurement of small grain sizes and the reduction of average grain size d.

3.2 Influence of phase volume fractions on microstructural heterogeneity

The spatial grain size dispersion is measured using the point-sampled intercept length method for different weld metals to quantify the grain structures heterogeneity; see Fig. 10. The arc and laser-hybrid weld metals show a clear bi-modal grain structure, consisting of fine-grained acicular ferrite and coarse-grained primary ferrite. The primary ferrite is quite equiaxed for both samples, but for the laser-hybrid weld metal, they are arranged in veins that seem to be consistent with the direction of the highest temperature gradient. The volume fraction of acicular ferrite is higher for the laser-hybrid weld, yielding a smaller average grain size. The volume fraction of acicular ferrite has been shown to have a linear relationship to the relative grain size dispersion, Δd/d [18]. The laser weld metal consisting of bainite and martensite also shows a large dispersion of grain sizes. The conventional definition of grain boundaries with 10° misorientation criteria has revealed many locations with small needle-shaped grains. However, there are several areas with coarse grains, where significant orientation gradients are also observed from the inverse pole figure; see Fig. 4. The coarse-grained appearance is partly due to the inconsistent misorientation across grain boundary segments, and thus, some of the boundaries are incomplete, and grain boundaries ‘bleed through’ in some locations.

Fig. 10
figure 10

Point-sampled grain size measured for the three weld metals, shown using the Hall–Petch parameter d−0.5 (µm−0.5), and thus, larger values indicate smaller grain size or higher strength

Full size image

Next, the adaptive domain misorientation approach is used to study the differences in the grain sub-structures. The misorientation threshold ΔθDDW = 0.5° has been shown to resolve the dislocation cell structure [26], and the angle is consistent with direct TEM observations of dislocation cell structures in polycrystalline BCC steel [20]. The adaptive domain misorientation and the dislocation cell size are shown for the entire maps in Fig. 11, and the regions highlighted by the dashed rectangles are shown enlarged in Fig. 12. The arc weld metal shows a limited amount of grain sub-structures, with some dislocation cells observed in the coarser primary ferrite grains. Only a limited amount of dislocation cells can be observed in the regions with acicular ferrite. In contrast, the primary ferrite in the laser-hybrid weld metal has a considerably larger amount of dislocation cells. The size of the dislocation cells is also smaller in comparison to the arc weld. The bainitic/martensitic laser weld metal has extremely fine sub-structures throughout the microstructure. The grain and dislocation cell size statistics (for the single EBSD maps) in Fig. 13 show that the laser weld metal has the largest volume-weighted average grain size dv and the broadest grain size dispersion Δd/d. The laser weld metal has the smallest average dislocation cell size at 0.68 µm compared to 0.83 µm for the laser-hybrid weld metal and 1.41 µm for the arc weld metal. Therefore, the ratio of dislocation cell size to volume-weighted average grain size is 59% for arc, 41% for laser-hybrid, and 20% for laser weld metals, correspondingly.

Fig. 11
figure 11

Adaptive domain misorientation (Δθ = 0.5°, nn = 60) showing dense dislocation walls and dislocation cells (top), and the estimated dislocation cell size in µm (bottom) for the three weld metals. The dashed rectangles indicate regions for more detailed analysis

Full size image
Fig. 12
figure 12

Close-up regions of the adaptive domain misorientation (Δθ = 0.5°, nn = 60) and dislocation cell size (displayed in micrometres) for the region highlighted in Fig. 11

Full size image
Fig. 13
figure 13

Comparison of grain size and dislocation cell size for the three weld metals. The values represent the individual EBSD scans shown in Figs. 10, 11, and 12

Full size image

3.3 Influence of grain and dislocation cell size on mechanical properties

The grain sub-structures also act as barriers to dislocation motion. Thus, the bainitic/martensitic laser weld is expected to be much stronger than indicated by its volume-weighted average grain size. The average hardness values of the three weld metals are shown in Fig. 14 to demonstrate the influence of grain sub-structure size on the mechanical properties. Based on Ref. [18], hardness is shown in Fig. 14A for many weld metals as a function of the volume-weighted average grain size. The base metals and ferritic weld metals consisting of acicular ferrite (AF) and primary ferrite (PF) are observed to follow one trend. On the other hand, the bainitic/martensitic (B/M) weld metals have a much higher hardness with the same grain size. This is especially the case for the laser weld metal with the fine dislocation cell structure. Considering the (volume-weighted) average dislocation cell size as the geometric dimension determining material strength, the disagreement between two types of weld metal microstructures becomes smaller; see Fig. 14B. Four additional samples were analysed to provide a slightly broader dataset for the analysis. Overall, the dislocation cell size seems to maintain the relationship between the AF/PF welds that are either arc or laser-hybrid welded. The B/M weld metals from laser-based welding processes show small dislocation cell sizes, shifting the data points to the right. While there is still a distinct change in slope, the results indicate that the sub-structural dimensions can provide further insight for predicting mechanical properties. Here it should be noted that the dislocation cell size is analysed from single EBSD scans. While they are chosen to be representative of the microstructures in general, they do not contain the complete spatial variation. Therefore, future work is needed to re-analyse all samples in terms of spatial dislocation cell size variation. In addition, the measurement methodology should be applied to different materials and welding processes to understand the applicability limitations better.

Fig. 14
figure 14

A Measured average hardness values plotted as a function of volume-weighted average grain size based on Ref. [18] and B the (volume-weighted) average dislocation cell size, with the three welds of this study highlighted in colour

Full size image

In addition to the grain size dependence of material properties, it has been shown that material strength can be predicted using dislocation density; see, e.g. [53, 54]. On the other hand, it has also been shown that the dislocation cell size is in proportion to dislocation density ρ−0.5 [55]. Therefore, the dislocation cell size measured by the adaptive domain misorientation approach may be a good measure for estimating mechanical properties. Further study is required to measure the dislocation density of the weld metals using, e.g. x-ray diffraction [56,57,58] and to determine the correlation with the adaptive domain misorientation approach. Greulich and Murr [59] modified the Hall–Petch relationship to include both grain size and dislocation cell size as individual factors for a shock-loaded nickel. A similar modification may be possible for the weld metals in the current study, as the sub-structural configurations are different for ferrite, bainite, and martensite. While there are significant differences in the dislocation cell size, the analysis should be extended to include the sub-grain size and the degree of deformation within the sub-structures as it affects the motion of dislocations. This is also related to the change in the slope of the Hall–Petch relationship for the different phase mixtures, shown in Fig. 14B. This may also be partially related to the general size effect at a feature size smaller than 1 µm; a gradual change in slope at d−0.5 > 1 has been observed for the yield strength of interstitial free steels through experiments and strain gradient plasticity simulations [60].

4 Conclusions

This paper combined the EBSD measurement of grain size with the recently developed adaptive domain misorientation approach to provide spatial information on the grain and dislocation cell size distribution for ferritic steel weld metals. The studied weld metals consisted of varying mixtures of primary ferrite, acicular ferrite, and bainite/martensite to represent a large variety of ferritic microstructures. Significant differences were measured in the grain size distribution, and especially in the spatial size distribution of dislocation cells for the bainitic/martensitic laser weld metal and the laser-hybrid weld metal consisting of primary and acicular ferrite.

Measurement of dislocation cell size is a novel feature of the adaptive domain misorientation approach, as it enables the dislocation cell structure to be studied using conventional EBSD. It was determined that while bainitic/martensitic microstructures have the smallest dislocation cells, the size of the dislocation cells is dependent on the welding method for primary ferrite. The arc-welded sample showed only a few large dislocation cells in the coarse primary ferrite grains, while the laser-hybrid weld metal had noticeable smaller dislocation cells in similarly sized primary ferrite grains. The initial analyses indicate that information about the sub-structures can provide insight for the differences observed in the strength properties of ferritic steel weld metals. Especially the martensitic weld metals with seemingly coarse average grain sizes had the smallest average dislocation cell sizes, and a Hall–Petch type relationship could be partially established based on dislocation cell size alone for considerably different phase volume fractions observed in the studied ferritic steel weld metals.

Further work is required to analyse the dispersion and spatial variation of grain sub-structures and to map the evolution of deformation for different initial grain sub-structure configurations. In addition, the introduced measurement methodology should be applied to other materials and welding processes to understand better the applicability limitations and the influence of welding methodology. The developed methods and used datasets are provided as open access.