Stress magnification factor for angular misalignment between plates with welding-induced curvature

Abstract

The construction of lightweight structures poses new design challenges as a result of the different mechanics of deformation experienced by thinner-plated structures. Because of a reduced bending stiffness, thin plates are particularly sensitive to welding-induced distortions, which include a curvature, in addition to the axial and global angular misalignment observed on thick plates. The curvature shape and amplitude determine a local angular misalignment at the welded joint, which causes non-negligible secondary bending effects. Therefore, the commonly used stress magnification factors k_m solution for flat plates need a further development to include the curvature effect. This study proposes new analytical formulations, which extend the applicability of the existing solutions to the assessment of the structural stress of a curved thin plate under an axial load. The improved formulations are consistent with the geometrical non-linear finite element analysis under compression (up to $\sim 80$% of the buckling limit) and tension (up to the yield strength). A sensitivity analysis is presented in order to show the dominant role of the curvature effect in the estimation of the k_m factor. Regardless of the load applied, the presence of the curvature causes a flat plate solution inaccuracy greater than 10% when the local angular misalignment is more than 1.25 times higher than the global angular misalignment in the case of a thin and slender structure.

1 Introduction

Prompted by energy efficiency and fuel economy reasons, the structural lightweight design for large-size structures has been in the spotlight of the recent research in several industrial fields. For instance, modern cruise ships have been designed to accommodate an increased number of cabins and open spaces, thus directing shipbuilding towards new solutions in terms of space and weight in order to increase the performance of the structure [1,2,3,4,5]. Thin-walled structures represent an optimum solution to achieve this design target. However, the implication of thinner structures poses new design challenges in terms of structural durability. The fatigue strength assessment is one of the key challenges, as thin structures show considerable susceptibility to manufacturing- and assembly-induced imperfections [6]. According to Remes et al. [4], a visible detrimental effect on the fatigue life of thin-walled marine structures is caused by welding. It has been demonstrated that less severe distortions may be obtained by low-heat-input welding methods such as laser-hybrid welding [1, 3, 7]. However, in general, the reduced bending stiffness of thin and slender plates leads to complex distortion shapes, and these geometrical imperfections cause a serious increase in stress at fatigue-critical welded joints.

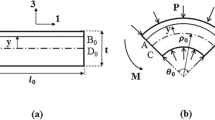
At present, the fatigue strength assessment of large structures such as ships is carried out by using the structural stress approach; see, e.g. [8,9,10]. The idealised 3D finite element model of a structure is created without modelling the distortions. Then the stress increase resulting from welding-induced distortions is considered separately in the computation of the stress magnification factor k_m. Different fatigue design codes and recommendations such as the IIW fatigue recommendations [9] classify the welding-induced imperfections as axial e and angular α misalignment. The first is related to the plates’ offset, and the latter to a linear lateral distortion y; see Fig. 1. This engineering approach was developed for flat plates and it has been successfully applied in the fatigue design of welded structures for several decades. Nevertheless, current manufacturing technologies such as laser-hybrid welding allow the welding of thinner plates, i.e. plates less than 5 mm thick, for which the flat plate assumption is violated. For thin (i.e. with a thickness t < 5 mm) and slender plates (i.e. L/t > 20, with L as the length between two supports), the distortion shape is observed to be curved, as shown in Fig. 2 [1, 4]. Therefore, the existing k_m factor formulations, derived according to the flat distortion shapes, cannot properly apply to the fatigue assessment of thin plates.

Fig. 1

Geometrical parameters describing the welding-induced imperfections [9]

Fig. 2

Welding-induced angular misalignment for thick and thin plates. Because of the curved shape, the local angular misalignment α_L differs from the global angular misalignment α_G, in the case of thin plates. [1]

In recent years, a considerable research effort has been devoted to developing a solid basis for the fatigue design of thin plates in large welded structures. On the basis of the experimental, numerical and theoretical analysis of small-scale and full-scale specimens, the fatigue behaviour of welded thin plates is better understood; see, e.g. [1,2,3,4, 7, 11, 12]. The curved distortion shape results in significant secondary bending stress at the welded joint and thus reduced fatigue strength. The special challenge is that this secondary bending stress has a non-linear relationship with the axial tensile load that is applied, as shown in Fig. 3. The non-linearity is related to the straightening effect, which causes the stress magnification factor k_m to decrease under an increased tensile load. Thus, the definition of the structural stress for welded thin plate structures requires the consideration of the actual distortion shape and geometrical non-linear finite element analysis [3]. Additionally, the previous research pointed out the dominant role of the local angular misalignment α_L also in the structural stress definition for full-scale structures, i.e. stiffened plate structures [12]. This study also shows that the simple half-sine function can be utilised in the geometry modelling of curved distortion shapes. On the basis of these findings, the development of an analytical k_m formulation for curved thin plates is an attractive alternative in order to avoid time-consuming finite element analyses.

Fig. 3

Non-linear trend of the stress magnification factor k_m with respect to the nominal stress. At the top right, the structural stress extrapolation for the weld toe is shown. [1]

The well-known non-linear analytical solutions for the stress magnification factor as a result of the angular misalignment were presented by Kuriyama et al. [13]. These solutions were developed for flat plates and implemented in, e.g. the IIW recommendations [9], and for pinned and fixed boundary conditions (BCs) they assume the forms shown in Eqs. 1 and 2.

$$ k_{m,angular}=1+\frac{{3}{\alpha}l}{2t}\frac{\tanh\left( \frac{\upbeta}{2}\right)}{\frac{\upbeta}{2}} $$

(1)

$$ k_{m,angular}=1+\frac{{3}{\alpha}l}{t}\frac{\tanh\left( \upbeta\right)}{\upbeta} $$

(2)

$$ {\upbeta}=\frac{2l}{t}\sqrt{\frac{3{\sigma_{m}}}{E}} $$

(3)

In the above formulations, l, t and α are the length, the thickness and the angular misalignment shown in Fig. 1b, respectively; σ_m is the tensile membrane stress that is applied; and E is the modulus of elasticity of the material (which is assumed to be linear-elastic). On the basis of the Euler-Bernoulli Theory, these equations were developed for distorted plates presenting a linear geometry, i.e. a straight and ideal beam. This model assumed that the welding-induced distortion is part of the idealised model, meaning that the secondary bending moment resulting from the linear lateral sway (y in Fig. 1b) is considered in the computation. As a result, the non-linear β-dependent coefficients in Eqs. 1 and 2 analytically describe the straightening effect caused by tensile loads. Their derivation follows the definition of the stress magnification factor k_m as the ratio between the Hot-Spot structural stress and the nominal stress applied to the structure, given that the developing deformation is involved in the structure equilibrium equation. The developing deformation is indeed included in terms of an additional bending moment, which results from the load-distortion interaction.

Recently, Shen et al. [14] have introduced a modified stress magnification factor to include the magnitude and shape curvature effect on welded thin plates. Relying on the Toshio formula ([15]) and modelling the initial curvature with a quadratic function, the proposed model has been validated against finite element analysis for fixed and simply supported BCs (see also [16]). A different approach has been proposed by Zhou et al. [5], who studied the butt weld-induced distortions of thin plates. The non-linear imperfect beam problem is converted into a non-linear perfect beam one. Specifically, angular and buckling distortion modes, as well as global and local angular distortions, have been modelled in terms of equivalent dummy loads applied to a perfect, i.e. straight, beam. The model is validated against numerical solutions, with both tensile and compression loading conditions being considered. These recent research studies provide valuable development steps in improving the analytical solution of the stress magnification factor for welded thin plates with curved distortions.

Given the state of the art of research, there is a need to establish an effective analytical model that is able to describe the overall welding-induced curved distortion effect on the stress state of a thin slender plate. This includes not only a deeper study of the influence of curvature, but also the selection of proper assumptions in order to make the model clear, simple and as versatile as possible. In the light of this consideration, this study derives an analytical model, intended to condense the effects of geometrical imperfections into the stress magnification factor k_m. Given that the axial misalignment affects thick and thin welded plates equally, the analysis focuses on the effect of the angular misalignment in global and local terms. Aiming at understanding the impact of the initial curvature effect among the other factors, a model sensitivity analysis is provided for tension and compression loading conditions. The analytical model will rely on the von Kármán Theory applied to an idealised structure solved by means of the slope deflection method and the linear superposition principle. The aim is to extend the validity of the analytical model provided for flat plates (implied by, e.g. the IIW recommendations) to welded curved plates by modelling a non-linear distortion. Thereby, the analytical derivation presented in this paper is intended to bring the currently recommended k_m solution for flat plates to an improved form, which includes the initial curvature effect into an additional higher order, i.e. non-linear, term. In this paper, the existing stress magnification factor caused by the angular misalignment (see Eqs. 1 and 2) is referred to as k_{m, glob}, which refers to the onset of a global angular misalignment between flat plates.

2 Method

2.1 Analytical model for a curved beam and the related k_m factor

The analytical model considers that a 1D beam element represents the longitudinal direction of the welded thin plate. The welded thin plate is assumed to have symmetric distortions with respect to the welded seam (see Fig. 2). Therefore, as a result of symmetry, only one side of the welded plate is considered, as shown in Fig. 4. The distorted shape is described by a half-sine curvature w_c(x) with its maximum amplitude a₀ at mid-length and a linear lateral sway w_s(x), which causes a vertical offset y₀ of the loaded end opposite to the origin of the beam. The respective functions are reported in Eqs. 4 and 5. In the analysis, the distortion is modelled according to the optical geometry measurements on fatigue test specimens of welded joints from [1].

$$ w_{c}(x)=a_{0}\sin\left( \frac{\pi x}{l}\right) $$

(4)

$$ w_{s}(x)=\frac{y_{0}x}{l} $$

(5)

In the model, the local angle α_L (see Fig. 4) is defined as in Eq. 6.

$$ \alpha_{L}=\alpha_{a_{0}}+\alpha_{y_{0}} $$

(6)

The two angle components are shown in Eqs. 7 and 8.

$$ \alpha_{a_{0}}=\arctan\left( \frac{d}{dx}a_{0}\cdot\sin\left( \frac{\pi x}{l}\right)\right)\vert_{x=0} =\arctan\left( \frac{a_{0}\pi}{l}\right) $$

(7)

$$ \alpha_{y_{0}}=\arctan\left( \frac{d}{dx}\frac{y_{0}x}{l}\right)\vert_{x=0} =\arctan\left( \frac{y_{0}}{l}\right). $$

(8)

Thus, the local angle α_L is equal to the global angle α_G only if the curvature amplitude a₀ is equal to zero (i.e. for a flat distorted shape).

Fig. 4

Idealised beam model of a welded distorted thin plate under static load (P > 0)

A remote load P is applied at the end opposite to the weld seam. Along with the boundary condition of the structure, it is shown in Fig. 4. As a result of symmetry at the weld seam location, this end is the fully fixed one. The loaded end has fixed or pinned BCs.

The fixed (i.e. clamped) boundary condition reflects the fatigue testing condition of small-scale specimens or the case of a welded plate supported by a panel frame. In these cases, the loaded end can be considered as clamped against bending rotation. This common approach was also considered by Lillimäe et al. [2]. However, on the basis of previous studies of stiffened panel structures (e.g. [12]), any boundary condition far away from the weld location does not have a significant effect, meaning that the beam end opposite to the weld location can be assumed to be a pinned end, i.e. the bending rotation is left free. Thus, this study assesses both the fixed and pinned beam configurations, which, according to what is explained above, differ only in terms of the bending rotation experienced at the loaded end (i.e. = 0 for a fixed end and ≠ 0 for a pinned end), while the deflection is left free. Given its slenderness, the small-scale specimen or a plate strip taken from welded thin plate structures could be treated as a 1D beam with negligible shear effects. Therefore, the displacement field from the classical Euler-Bernoulli Theory (EBT) applies to such a problem. In order to include the effect of the geometrical non-linearity, the von Kármán strain solution for small displacement and moderate rotation is considered; see, e.g. [18]. The principle of virtual displacement allows the governing equations of motion to be computed by also superimposing the initial shape onto the developing deflection. As a result of the effect of the geometrical non-linearity, the beam problem is statically indeterminate and the slope deflection method is applied to achieve a closed-form solution. Moreover, given the validity of the superposition principle, a step-by-step process is used for an easy approach in which the effects of the lateral sway and the curvature are decoupled. The beam is considered to be made of an isotropic homogeneous material with a modulus of elasticity E. The material is assumed to remain elastic since only small-scale yielding at the notch tip exists in the high-cycle fatigue range. Below, the analytical solution is formulated for tension loading and then also expanded for compressive loading in Section 2.7.

2.2 Geometrical non-linearity formulation for curved beam

On the basis of the Bernoulli-Navier hypotheses (see, e.g. [18, 19]), the displacement field that describes the mechanical behaviour of the beam is represented in Fig. 5 and expressed in Eq. 9. The beam displacement field components (u₁, u₂, u₃) respectively indicate the total displacement in the (x, y, z) directions.

Fig. 5

Euler-Bernoulli beam axial displacement [18]

$$ \left\{\begin{array}{lll} u_{1}(x) &=u(x)-z\frac{dw}{dx} \\ u_{2}(x) &=0 \\ u_{3}(x) &=w(x) \end{array}\right. $$

(9)

In Eq. 9, z is the transverse coordinate measured from the centroid of the cross-section and x is the longitudinal coordinate. u is the axial displacement, while w is the transverse displacement of a point on the x-axis with respect to the centroid of the cross-section of the beam [18]. As explained in the literature (e.g. [18, 19]), the axial strain of the beam can be obtained by imposing the displacement field onto the Green-Lagrange tensor component $E_{ij}=\frac {1}{2}(\frac {\partial u_{j}}{\partial x_{k}}+\frac {\partial u_{k}}{\partial x_{j}}+\frac {\partial u_{m}}{\partial x_{j}}\frac {\partial u_{m}}{\partial x_{k}})$, which, for a beam, reduces to the axial strain E₁₁ ≈ ε_xx in Eq. 10.

$$ \begin{array}{@{}rcl@{}} \varepsilon_{xx}&=&\frac{\partial u_{1}}{\partial x_{1}}+\frac{1}{2}\left( \frac{\partial u_{3}}{\partial x_{1}}\right)^{2}\\ &=&\left[\frac{du(x)}{dx}+\frac{1}{2}\left( \frac{dw}{dx}\right)^{2}\right]-z\frac{d^{2}w(x)}{dx^{2}}\\ &=&\varepsilon^{0}_{xx}+z\varepsilon^{1}_{xx} \end{array} $$

(10)

The term in square brackets in Eq. 10 is the extensional deformation, while the second term describes the bending strain. The axial strain thus determined is known as the von Kármán strain and properly accounts for small displacement and moderate rotation. The related axial stress is determined according to Hooke’s law in Eq. (11).

$$ {\sigma_{xx}(x)}= E{\varepsilon_{xx}(x)} $$

(11)

By applying the principle of virtual displacement (see Eq. 12) to the bending beam, the governing differential equation of motion can be found. The procedure is shown by [18, ch.5].

$$ \begin{array}{@{}rcl@{}} dW_{TOT}& = &dW_{I}+dW_{E}\\ & = &{{\int}^{l}_{0}}\left[N_{xx}\frac{d\delta u}{dx} + \frac{dw}{dx}\frac{d\delta w}{dx}N_{xx}-\frac{d^{2}\delta w}{dx^{2}}M_{xx}\right]dx\\ &&-P\delta u(l)=0 \end{array} $$

(12)

In Eq. 12, N_xx and M_xx are the internal axial force and bending moment. They are defined positively as in Fig. 6. In the figure and in the following derivation, they are addressed as simply N and M, respectively. The x-coordinate dependence is implied.

Fig. 6

Ends and internal actions on the simplified pre-deformed Beam element

Since the virtual displacements δu and δw are independent, it is possible to determine two governing equations of equilibrium for a beam that is only subjected to a tensile point load P; see Eq. 13.

$$ \left\{\begin{array}{ll} \delta u:&-\frac{dN}{dx}=0\\ \delta w:&-\frac{d}{dx}(\frac{dw}{dx}N)-\frac{d^{2}M}{dx^{2}}=0 \end{array}\right. $$

(13)

Focusing on the deflection of the beam, by integrating twice and including the initial shape of the beam w₀, the equation becomes: − N(w + w₀) − M + Ax + B = 0, where A and B are the integration constants to be determined by applying the model boundary conditions (BCs). In terms of nodal forces, the BCs are shown in Eq. 14.

$$ \begin{array}{@{}rcl@{}} N(0)&=&-P \quad ~V(0)=V_{a} \quad M(0)=M_{a}\\ N(l)&=&P \quad\quad V(l)=V_{b} \quad ~M(l)=M_{b} \end{array} $$

(14)

In Section 2.3, these BCs are applied along with the null nodal displacement at the beam ends in order to obtain the governing ordinary differential equations (ODEs) of the two beam models.

The ODEs are derived by applying the definition of the bending moment in Eq. 15 to − N(w + w₀) − M + Ax + B = 0.

$$ M(x)={\int}_{A}{z\sigma} dA=-E{\int}_{A}{\epsilon}z dA= E{\int}_{A}\frac{z^{2}}{\rho} dA= \frac{EI}{\rho} $$

(15)

In Eq. 15, $I={\int \limits }_{A}z^{2} dA$ is the principal moment of inertia of the cross-section of area A and the bending strain ε is defined as the ratio $\left (\frac {z}{\rho }\right )$. ρ is the curvature radius of the deflected axis as shown in Fig. 7. Such a radius is linearised as in Eq. 16, where $w^{\prime \prime }$ is the second derivative of the deflection w with respect to the length coordinate x. This approximation results in an error of about 1% if the maximum of the first derivative $w^{\prime }$ does not exceed 0.08, i.e. less than 5° [17].

$$ \frac{1}{\rho}=\frac{w^{\prime\prime}}{(1+w^{\prime2} )^{\frac{3}{2}}}\thickapprox w^{\prime\prime} $$

(16)

Fig. 7

Bending of a straight bar according to the Bernoulli-Navier Hypothesis. (Modified from [17])

Applying the approximation in Eq. 16, the differential equation of bending for small deformations of a slender beam is found in Eq. 17. Notice that this approximation applies for tension loading condition, as the error reaches inappropriate percentages only for very large distortions that cause critical secondary bending effects to the structure. However, it may significantly affect the accuracy of the solution for compression loads, especially when the structure approaches the buckling instability. For this reason, some consideration about the validity of the approximation is provided in Section 4.1.

$$ M(x)=-EIw^{\prime\prime}(x) $$

(17)

On this basis, the geometrical non-linearity is considered by the superposition of the effects in the lever arm of the tensile load P. The superposition principle is considered an approach that approximates well for beams with small geometrical imperfections [19]. The slope deflection method is a useful way to solve the indeterminate problem, as suggested by Aristizabal-Ochoa [20] for a second-order analysis of an imperfect beam with semi-rigid connections, subjected to a compressive axial load and additional transverse actions. In [20], the solving method is based on approximation with a sine Fourier series, which has been shown to be sufficiently accurate to describe the beam-column deflection under compression, i.e. for the buckling analysis [19]. The initial deformation is modelled as a sine series, and the lateral sway is addressed as well. In [20], the initial imperfections result in additional transverse loads proportional to the bending stiffness and magnitudes of the imperfections of the beam-column, thus increasing the lateral deflection and the effective bending loading condition. The elastic bending connections at the two ends a and b are modelled with the stiffness k_a and k_b in the plane of bending of the beam. The stiffness indices in Eq. 19 vary between 0 and $\infty$, so they are replaced, for the sake of convenience, with fixity factors (see Eq. 19) varying between 0 (simple connection) and 1 (rigid connection). In Eq. 18, EI is the flexural rigidity of the beam, while h indicates its length, as in Fig. 8. The figure represents the general model in the study conducted in [20].

$$ R_{(a,b)}=\frac{k_{(a,b)}}{\frac{EI}{h}} $$

(18)

$$ \rho_{(a,b)}=\frac{1}{\left( 1+\frac{3}{R_{(a,b)}}\right)} $$

(19)

In this study, ideal BCs are used, so that the fixity factor for fixed bending rotation is equal to 1 (i.e. a fully rigid connection), while the pinned end corresponds to 0 (i.e. a non-rigid connection). The present case also neglects any load other than the axial one and axial load eccentricities addressed as e_a and e_b in the mentioned article.

Fig. 8

Structural model of an imperfect column with sidesway partially inhibited and rotational end restraints. Eccentric axial loads are applied to the column extremes. (Modified from [20])

2.3 Stability analysis of imperfect beams by using the superposition principle

The procedure used to solve the beam stability analysis consists of four main stages:

• 1. computation of deflection and slope deflection equations of the loaded beam with initial curvature;

• 2. computation of deflection and slope deflection equations of the loaded beam with linear lateral sway;

• 3. derivation of the total deflection and slope deflection equations by linear superposition of the functions from the previous steps;

• 4. determination of the unknowns of the problem (i.e. computation of the final solution).

Any static analysis concerning the beam equilibrium refers to Fig. 6 in order to fix a conventional system. In the figure, the beam is displayed with the positive forces and moments involved in its equilibrium condition.

• Stage 1 The first stage requires consideration of the initial curvature only, thus excluding the lateral sway y₀. Moreover, the selected BCs related to the deflection of the model are introduced in the second stage, while the curvature is considered on a simply supported beam.

  By imposing the BCs in Eq. 14 onto the equilibrium − N(w + w₀) − M + Ax + B = 0, and using Eq. 17, the governing ODE can be obtained; see Eq. 21. For a simply supported beam, M_a = M_b = 0 and the beam ends have null deflection, as indicated in Eq. 20. w₁(x) is the deflection resulting from the initial curvature of the loaded beam.

  $$ \left\{\begin{array}{ll} w_{1}(0)&=0 \\ w_{1}(l)&=0 \end{array}\right. $$

  (20)
  $$ w_{1}^{\prime\prime} \left( x\right)-{k}^{2}w_{1}\left( x \right)=+k^{2}a_{0}\sin\left( \frac {\pi x}{l}\right) $$

  (21)

  In Eq. 21, k replaces the quantity $\sqrt {P/EI}$. The solution to this equation generally assumes the form $w_{1}(x)=C\sinh (kx)+D\cosh (kx)+b\sin \limits \left (\pi x/l\right )$, where C and D are constants. The hyperbolic functions model the homogeneous solution, while the harmonic one is the particular solution resulting from the action of P on the initial curvature. The solution to the ODE is found by imposing the BCs related to the beam deflection in Eq. 20. This implies C = D = 0, while the coefficient b is found by substitution of the particular solution into the differential equation. The resulting deflection curve and slope deflection equation resulting from the sinusoidal initial curvature under tensile load P is finally obtained; see Eq. 22.

  $$ \left\{\begin{array}{ll} w_{1}(x)&=-{\frac {({kl})^{2}a_{0}}{({kl})^{2}+{\pi}^{2}}\sin \left( {\frac {\pi x}{l}} \right) }\\ w^{\prime}_{1}(x)&= -\frac {a_{0}l\pi {k}^{2}}{({kl})^{2}+{\pi}^{2}}\cos \left( {\frac {\pi x}{l}} \right) \end{array}\right. $$

  (22)

• Stage 2 The second stage of the analysis addresses the lateral sway imposed onto the cantilever beam. As seen for the initially curved beam in Stage 1, the resulting ODE is obtained by imposing the BCs in Eq. 14 and the nodal deflection in Eq. 23. The ODE is reported in Eq. 24. w₂(x) is the deflection of the beam with initial lateral sway, under tension.

  $$ \left\{\begin{array}{ll} w_{2}(0)&=0 \\ w_{2}(l)&={\Delta}-y_{0} \end{array}\right. $$

  (23)
  $$ w^{\prime\prime}_{2}\left( x \right) -{k}^{2}w_{2} \left( x \right) =-\frac {M_{a}}{EI}+\frac{M_{a}+M_{b}- P({\Delta}-y_{0})}{EIl}x $$

  (24)

  The solution to the ODE assumes the form $w_{2}(x)=C\cosh (kx)+D\sinh (kx)+Fx+G$, where C, D, F and G are the constants to be found by imposing the deflection BCs above. The deflection and slope deflection equations result as in Eq. 25.

  $$ \left\{\begin{array}{ll} w_{2}(x)&=-\frac{M_{a}\cosh(kx)}{P}+\frac{M_{b}+M_{a}\cosh(kl)\sinh(kx)}{P\sinh(kl)}-\\ &+\frac{(M_{a}+M_{b}-P({\Delta}-y_{0}))x}{l}+\frac{M_{a}}{P}\\ w^{\prime}_{2}(x)&=-\frac{M_{a}k\sinh(kx)}{P}+\frac{M_{b}+M_{a}\cosh(kl)k\cosh(kx)}{P\sinh(kl)}-\\ &+\frac{M_{a}+M_{b}-P({\Delta}-y_{0})}{l} \end{array}\right. $$

  (25)

  From the total equilibrium equation of the beam in Fig. 6, the term Δ is derived, as in Eq. 26.

  $$ M_{a}+M_{b}-V_{b}l-P({\Delta})=0\rightarrow{\Delta}=\frac{M_{a}+M_{b}}{P}, $$

  (26)

  where V_a = V_b = 0 for both the models.

• Stage 3 The principle of superposition is applied to obtain the total deflection w(x), the slope deflection $w^{\prime }(x)$ equations and the bending moment distribution related to a distorted beam column under tension; see Eqs. 27 and 28. In the following equations, the term (kl) is replaced by Φ, as also indicated by [20].

  $$ \left\{\begin{array}{ll} w(x)&=w_{1}(x)+w_{2}(x)\\ w^{\prime}(x)&=w_{1}^{\prime}(x)+w_{2}^{\prime}(x) \end{array}\right. $$

  (27)

  The bending moment distribution over the beam length is computed with reference to Eq. 17.

  $$ \begin{array}{@{}rcl@{}} M(x)&=&M_{a}\cosh(kx)-\frac{(M_{b}+M_{a}\cosh({\Phi}))\sinh(kx)}{\sinh({\Phi})}-\\ &&+\frac{{\Phi}^{2}}{{\Phi}^{2}+\pi^{2}}\left( \frac{\pi}{l}\right)^{2}a_{0}\sin\left( \frac{\pi x}{l}\right) \end{array} $$

  (28)

• Stage 4 In order to determine the unknowns and solve the problem, the slope deflection method is applied: the slope BCs are imposed onto the slope deflection equations computed at the beam ends (i.e. θ_a and θ_b). At this stage, the term Δ is substituted according to Eq. 26. Imposing the slope BCs requires a separate derivation for the two models with fixed and pinned boundary conditions, which are respectively analysed in Sections 2.5 and 2.6. The slope deflection equations at the beam ends are obtained as in Eq. 29.

  $$ \left\{\begin{array}{ll} \theta_{a} &=w^{\prime}(0)\\ \theta_{b} &=w^{\prime}(l) \end{array}\right. $$

  (29)

2.4 k_m factor derivation

The results from the stability analysis described above lead to the analytical computation of the normal stress distribution along the beam length as a function of the coordinate x. According to the stress-strain constitutive law (see Eq. 11), the structural stress includes a membrane (i.e. axial) stress and a bending one as the related strain.

$$ \sigma_{structural}(x)=\sigma_{m}(x)+\sigma_{b}(x) $$

(30)

The membrane stress σ_m and the bending stress σ_b are defined as in Eq. 31.

$$ \left\{\begin{array}{ll} \sigma_{m}(x)&=\frac{P}{bt}\textit{constant ~over~ beam ~thickness ~and ~length}\\ \sigma_{b}(x)&=\frac{M(x)z}{I} \end{array}\right. $$

(31)

From Eq. 31, it is clear that the bending moment distribution determines the structural stress trend over the beam length. Figure 9 represents an example of the top and bottom surface stresses for the two configurations. The weld is located to x = 0 m. It is pointed out that the critical stress, i.e. the Hot-spot structural stress in Eq. 32, is experienced at the location of the weld, on the top surface ($z=\frac {t}{2}$). Figure 10 shows that the normal stress is linearly distributed over the thickness, according to the basic hypothesis of the theory, and reaches its peak on the top surface.

$$ \begin{array}{@{}rcl@{}} \sigma_{HS} & =&\sigma_{m}+\sigma_{b}\left( 0\right)\vert_{z=\frac{t}{2}}\\ & =& \frac{P}{bt}+\frac{M_{a}}{I}\frac{t}{2} \end{array} $$

(32)

Eventually, the computation of the stress magnification factor followed by using its definition.

$$ k_{m}=\frac{\sigma_{HS}}{\sigma_{m}} $$

(33)

Fig. 9

Example of the normal structural stress distribution along the beam length. Hot-spots result in the weld location at x = 0 m

Fig. 10

Structural stress distribution over the beam thickness at the weld location (red line). The Hot-Spot structural stress (HSS) is experienced by the top surface

2.5 Fixed-end configuration under tension

The step-by-step analytical derivation in Section 2.3 leads to the computation of the slope deflection equations for the fixed-end beam. The Stage 4 and the final k_m derivation are presented below.

• Stage 4 As suggested by [20], the slope deflection equations at the beam end θ_a and θ_b are computed and adapted into a matrix form; see Eq. 34.

  $$ \left\{\begin{array}{ll} \theta_{a}+\left( \frac{{\Phi}^{2}}{{\Phi}^{2}+\pi^{2}}\right)\frac{\pi a_{0}}{l}+\frac{y_{0}}{l}\\ \theta_{b}-\left( \frac{{\Phi}^{2}}{{\Phi}^{2}+\pi^{2}}\right)\frac{\pi a_{0}}{l}+\frac{y_{0}}{l} \end{array}\right\}=\left[\begin{array}{cc} S_{1} & S_{2}\\ S_{3} & S_{4} \end{array}\right]\left\{\begin{array}{ll} M_{a} \\ M_{b} \end{array}\right\} $$

  (34)

The terms S_1(2,3,4) are defined below.

$$ \begin{array}{@{}rcl@{}} S_{1}&=&S_{4}=\frac{1}{\frac{EI}{l}{\Phi}}\frac{\cosh({\Phi})}{\sinh({\Phi})}\\ S_{2}&=&S_{3}=\frac{1}{\frac{EI}{l}{\Phi}}\frac{1}{\sinh({\Phi})} \end{array} $$

(35)

In order to isolate the unknowns M_a and M_b, the inverse of the coefficients matrix is computed. The resulting system is shown in Eq. 37. The slope deflection method requires the application of the slope BCs in Eq. 36, which for this case are described in Eq. 36.

$$ \left\{\begin{array}{ll} \theta_{a}=w^{\prime}(0)&=0 \\ \theta_{b}=w^{\prime}(l)&=0 \end{array}\right. $$

(36)

$$ \left\{ \begin{array}{ll} M_{a} \\ M_{b} \end{array}\right\}=\left[\begin{array}{cc} r & s\\ s & r \end{array}\right]\left\{\begin{array}{ll} \left( \frac{{\Phi}^{2}}{{\Phi}^{2}+\pi^{2}}\right)\frac{\pi a_{0}}{l}+\frac{y_{0}}{l}\\ -\left( \frac{{\Phi}^{2}}{{\Phi}^{2}+\pi^{2}}\right)\frac{\pi a_{0}}{l}+\frac{y_{0}}{l} \end{array}\right\} $$

(37)

In Eq. 37, r and s correspond to the expressions in Eq. 38.

$$ \begin{array}{@{}rcl@{}} && r=\frac{1}{\frac{EI}{l}{\Phi}}\frac{\cosh({\Phi})}{\sinh({\Phi})}\\ && s=-\frac{1}{\frac{EI}{l}{\Phi}}\frac{1}{\sinh({\Phi})} \end{array} $$

(38)

Equation (39) presents the final solution for the bending moment experienced at the weld location. The formula is simplified by applying the hyperbolic function properties.

$$ M_{a} = \frac{\Phi EI}{l}\left[\tanh\left( \frac{\Phi}{2}\right)\frac{y_{0}}{l} + \frac{1}{\tanh\left( \frac{\Phi}{2}\right)}\left( \frac{{\Phi}^{2}}{{\Phi}^{2}+\pi^{2}}\right)\frac{\pi a_{0}}{l}\right] $$

(39)

k_m factor derivation

The k_m factor derivation based on Eqs. 32 and 33 and using I = bt³/12 in Eq. 39 is obtained for the fixed-end configuration (see Eq. (41)). The term ${\Phi }=\sqrt {\frac {P}{EI}}l$ is replaced by β on the basis of the nomenclature utilised by, e.g. the IIW recommendations; see Eq. 40.

$$ \upbeta=\frac{2l}{t}\sqrt{\frac{3\sigma_{m}}{E}} $$

(40)

$$ k_{m}=1+\frac{3y_{0}}{t}\frac{\tanh\left( \frac{\upbeta}{2}\right)}{\frac{\upbeta}{2}}+\frac{6a_{0}\pi}{t}\frac{\upbeta}{(\pi^{2}+{\upbeta}^{2})\tanh\left( \frac{\upbeta}{2}\right)} $$

(41)

For the sake of simplicity, in Section 4.2, the discussion refers to β-dependent coefficients to recall the terms in Eqs. 42 and 43.

$$ C1_{f}=\frac{\tanh\left( \frac{\upbeta}{2}\right)}{\upbeta} $$

(42)

$$ C2_{f}=\frac{\upbeta}{(\pi^{2}+{\upbeta}^{2})\tanh\left( \frac{\upbeta}{2}\right)} $$

(43)

These terms are multipliers of $\left (6y_{0}/t\right )$ and $\left (6a_{0}\pi /t\right )$, respectively. These coefficients may also be called straightening coefficients, since they quantify the non-linear straightening experienced by the distorted beam under tension. In general (i.e. for any load applied), they weight the lateral sway and initial curvature effects on the beam stress state.

2.6 Pinned end configuration under tension

The computation below refers to the assumption of the pinned-end beam.

• Stage 4 In this case, the BCs to be applied at the beam ends are indicated in Eq. 44.

  $$ \left\{\begin{array}{ll} \theta_{a}&=0\\ M_{b}&=0 \end{array}\right. $$

  (44)

By applying the conditions in Eq. 44, the system of the two slope deflection equations θ_a and θ_b is obtained. The slope deflection equation at the beam end a (i.e. θ_a) allows its only unknown M_a to be determined. Thereby, the problem is solved, including the bending moment distribution shown in Fig. 9b.

k_m factor derivation

The k_m factor that is developed is described by Eq. 45.

$$ k_{m}=1+ \frac{6y_{0}}{t}\frac{\tanh(\upbeta)}{\upbeta}+\frac{6a_{0}}{t}\frac{\pi\upbeta\tanh({\upbeta})}{(\pi^{2}+{\upbeta}^{2})} $$

(45)

The related β-dependent coefficients are C1_p and C2_p.

$$ C1_{p}=\frac{\tanh(\upbeta)}{\upbeta} $$

(46)

$$ C2_{p}=\frac{\upbeta\tanh({\upbeta})}{(\pi^{2}+{\upbeta}^{2})} $$

(47)

2.7 Solution for compression

The equations derived to estimate the k_m factor under tension allow for the stress computation in compression, given that the force P is applied with a negative sign. Analytically, having a negative force implies the definitions in Eq. 48.

$$ \begin{array}{@{}rcl@{}} P<0\Rightarrow k^{*}&=&\sqrt{\frac{P}{EI}}=i\sqrt{\frac{\vert P\vert}{EI}}=ik\Rightarrow {\Phi}^{*}={\upbeta}^{*}\\ &=&i\left( \frac{2l}{t}\right)\sqrt{\frac{3\vert\sigma_{m}\vert}{E}}=i\upbeta \end{array} $$

(48)

Knowing also that $\tanh ({\upbeta }^{*})=\tanh (i\upbeta )=i\tan (\upbeta )$, Eq. 41 changes into Eq. 49.

$$ k_{m}=1+\frac{3y_{0}}{t}\frac{\tan\left( \frac{\upbeta}{2}\right)}{\frac{\upbeta}{2}}+\frac{6a_{0}\pi}{t}\frac{\upbeta}{(\pi^{2}-{\upbeta}^{2})\tan\left( \frac{\upbeta}{2}\right)}. $$

(49)

Similarly, Eq. 45 changes into Eq. 50.

$$ k_{m}=1+ \frac{6y_{0}}{t}\frac{\tan(\upbeta)}{\upbeta}+\frac{6a_{0}\pi}{t}\frac{(-\upbeta\tan({\upbeta}))}{(\pi^{2}-{\upbeta}^{2})} $$

(50)

Under compression, the β-dependent coefficients (multipliers of $\left (6y_{0}/t\right )$ and $\left (6a_{0}\pi /t\right )$) are determined in Eqs. 51 and 52 for the fixed beam, and Eqs. 53 and 54 for the pinned beam.

$$ C1_{f}^{-}=\frac{\tan\left( \frac{\upbeta}{2}\right)}{\upbeta} $$

(51)

$$ C2_{f}^{-}=\frac{\upbeta}{(\pi^{2}-{\upbeta}^{2})\tan\left( \frac{\upbeta}{2}\right)} $$

(52)

$$ C1_{p}^{-}=\frac{\tan(\upbeta)}{\upbeta} $$

(53)

$$ C2_{p}^{-}=\frac{-\upbeta\tan({\upbeta})}{(\pi^{2}-{\upbeta}^{2})} $$

(54)

3 Sensitivity analysis of the curvature effect

3.1 Geometries and boundary conditions studied

The numerical analysis is carried out for varied geometrical shapes in order to validate the k_m formulations that are developed (see Eqs. 41, 45, (49) and (50)) and to study the effect of a curved shape on the k_m factor, i.e. the Hot-Spot structural stress that is experienced, as a function of the nominal stress. The analysis is limited to the plate specimens, i.e. beams. The beams are made of steel for welded thin plates in ship decks with a modulus of elasticity E = 206.8 GPa and Poisson’s ratio v = 0.3. During the analysis, the beam cross-section dimensions and length are varied. Based on small-scale, 3-mm-thick specimen dimensions, a slenderness ratio of 42 and aspect ratio (i.e. width-to-thickness ratio) of 6.67 are chosen.While, in relation to ship deck plate dimensions, the slenderness and aspect ratios selected are 300 and 100, with a thickness of 4 mm (see [1]). The analysis considers both tension and compression. The load range for tension is from 1 to 300 MPa, while for compression the analysis is from 0 MPa to the critical buckling load of the beam, i.e. the Euler load; see Appendix about buckling limit calculations. Furthermore, for compression loading, the variation in the slenderness ratio is limited since high slenderness ratios (e.g. > 100) do not allow for meaningful analyses because of the low buckling limit. All the analyses include both the fixed and pinned boundary conditions at the loaded beam end. The influence of the distortion shape is analysed by varying the angle ratio α_L/α_G between 1 and 40 under tension or 1 and 5 under compression. This allows slightly-to-heavily-curved components to be analysed. On the evidence of previous studies ([3, 12]), the local angle is likely to be less than 5°. In this study, a wider range is considered, thus enabling a deeper study of the curvature effect. The lateral sway y₀ is kept constant and equal to 5 mm, as the terms accounting for it in Eqs. 45 and 41 have already been validated earlier and are commonly used, e.g. in the IIW recommendations [9]. The selection of 5 mm is based on the earlier experimental measurements in [3].

3.2 Finite element analysis for validation

Finite element analysis is carried out for the selected geometry configurations in order to validate the analytical model and the related results. The geometry of the FE models is designed on FEMAP (v11.4.1), and the ABAQUS solver (v6.14-1) is used. Specifically, the modified RIKS method is applied to run the static analysis for non-linear geometries. Such analysis runs under the assumption of large deflections and provides the behaviour of the structure through linear extrapolation, also considering the non-linearity caused by the change in the initial distortion due to tension or compression load. ABAQUS default options are used for the required analysis settings (see [21]). Thereby, the convergence criteria for the analysis are a minimum arc length increment of 10^− 5 and a maximum number equal to steps of 100. Figure 11 shows the model for validation under tension in case of slenderness ratio 300. The 1-D beam element is subjected to a concentrated, constant force P applied at the right-hand side, positive in the x-direction. The BCs imposed onto the two beams are indicated in the same figure. By reference to the displayed global coordinate system, the component is clamped at its origin in x = 0 m (i.e. the left-hand side), while the remaining nodes over its length are constrained to guarantee a y-symmetry condition. This implies that the displacement in the y-direction (TY) and the rotations about the x- and z-axes (RX and RZ, respectively) are fixed for both the models, as shown in Fig. 11. In addition, the rotation about the y-axis (RY) is zero at the loaded end for the fixed end configuration. The FE mesh created for the beam with slenderness and aspect ratios 300 and 100, respectively, consists of 600, 2-noded elements of type B31 with a length of 2 mm each. A convergence analysis, based on the consistency of the structural stress concentration at the weld location (i.e. x = 0 m), shows that the analyses conducted with 2-mm-long elements agree with those using the element lengths 1 and 0.5 mm (the maximum percentage difference with the finest mesh is below 0.04%). Before the analyses are run, the nodal coordinates (x, y, z) of the model input files are modified according to Eq. 55. Thus, the initial deflection of the nodes represented in Fig. 11 (see curved line in black) is measured with respect to the non-deformed beam axis (i.e. the blue, straight line).

$$ z=a_{0} sin(\frac{\pi x}{l})+\frac{y_{0}x}{l} $$

(55)

The model analysed under compression is similarly designed, given the specified dimensions and loads. According to the same type of convergence analysis, the small-scale model is meshed by using 125 B31 beam elements with a length of 1 mm each. The smaller dimensions of the beam allow such a mesh to provide a more accurate solution without time-consuming simulations through buckling instability.

Fig. 11

FE model of the beam under a tensile load P. The BCs for the a fixed-end and b pinned-end model are indicated

4 Influence of curvature and geometrical non-linearity

4.1 Effect of the geometrical non-linearity on the k_m factor

The effect of the geometrical non-linearity is studied for tension and compression loading. Figure 12 shows the stress magnification factor k_m as a function of the applied tensile nominal stress, i.e. the membrane stress, in the case of a slenderness ratio of 300. The results are given for both fixed and pinned boundary conditions, as well as different distortion amplitudes, i.e. local angular misalignment values. The comparison between the analytical model and the FEA shows very similar results, having a maximum difference below 2%. About the curvature approximation, Eq. 16 is always valid (i.e. $w^{\prime }(x)\leq 0.08$), except when very large angle ratios (e.g. 40) make the slope reach peaks of about − 0.18. Nevertheless, this results in small errors.

Fig. 12

Stress magnification factor (k_m vs σ_m) as a function of applied tensile membrane stress for different local deformation angles and boundary conditions (fixed vs. pinned). α_G ≈ 0,25°

In the figure, the FEA results are plotted with points, while the lines describe the results of the analytical k_m models; see Eqs. 41 and 45. As shown in Fig. 12, a high geometrical non-linearity effect is observed for all the results. In the figure, the non-linearity of the relationship between the structural and membrane stress (i.e. the k_m factor) increases as the local angular misalignment increases. This behaviour is the result of the straightening effect, which significantly reduces the k_m factor, since the initial distortion is reduced as a function of the increased load. For high slenderness ratios, this straightening effect is very important. For instance, the fixed beam experiences a state of stress that results in a reduction of nearly 85% in the k_m factor when the load stress applied σ_m varies from 1 to 300 MPa. The results in Fig. 12 also show a remarkable increase in the k_m factor as a result of the presence of the initial curvature. In general, it dominates the response of the structure, while the lateral sway is relatively negligible. The results also show that the influence of the BCs on the slender beam under tension is only visible for very low load levels.

The geometrical non-linear behaviour for compressive loading is presented in Figs. 13 and 14. They show the stress magnification factor k_m as a function of the applied compressive nominal stress σ_m with a slenderness ratio of 42. Both the fixed and pinned BCs are analysed by varying the angle ratio α_L/α_G between 1 and 5. Similarly to the tension loading, the geometrical non-linearity effect is significant and the analytical results are consistent (i.e. with less than a 2% error) with FEA solutions up to around 80% of the beam’s buckling load σ_cr. The critical buckling loads are − 97 and − 24 MPa for fixed and pinned boundary conditions, respectively. The departure observed between analytical and numerical results close to the buckling load suggests that the analytical model that is developed does not apply when the beam approaches the instability. In order to extend its validity range, the approximation of the curvature in Eq. 16 should be relaxed. Indeed, for a beam with pinned BCs and with a large angle ratio (e.g. ≥ 5), the slope over the length of the beam can be higher than (±)0.2. As a result, the approximation causes more than 10% error at about 80% of the buckling load. Thereby, in case of very large distortions and high loading condition, it must be taken into account that the present model is not reliable.

Fig. 13

Stress magnification factor (k_m vs σ_m/σ_cr) as a function of applied compression membrane stress percentage with respect to the buckling load, for different local angles. Fixed end beam

Fig. 14

Stress magnification factor (k_m vs σ_m/σ_cr) as a function of applied compression membrane stress percentage with respect to the buckling load, for different local angles. Pinned end beam

In Figs. 13 and 14, the lines are obtained by using the formulations in Eqs. 49 and 50. All the results refer to the top surface of the beam. The geometrical non-linear behaviour for compressive loading differs from the behaviour for tension loading. Furthermore, under compression, the fixed and pinned beams show different behaviours. Figure 13 presents the non-linear increase of k_m caused by an increasing compression load. Divergence to $+\infty$ indicates that an unstable condition is reached close to the buckling limit of the beam, regardless of the magnitude of the initial distortion. In fact, the curvature has a greater impact away from the unstable region, where larger local angular misalignment implies a greater k_m. On the contrary, in Fig. 14, the influence of increased local angular misalignment is not observable for compression loads below about 20% of the buckling load. Above such a load level, the geometrical non-linearity causes a non-linear relationship between k_m and the nominal stress σ_m, and the local curvature starts to affect the stress state magnification. In this case, the straight beam (i.e. with α_L/α_G = 1) undergoes the highest stress concentration. As the local angle increases, the k_m factor decreases until the beam experiences a change in the deformation mechanism, which turns the top surface stress into tension (i.e. negative k_m values). The analytical formulation in Eq. 50 also allows the structural stress estimation to accurately take into account such complex phenomena.

4.2 Non-linear behaviour of the β-dependent coefficients

As shown in Section 2.7, the non-linearity of the formulations that were developed for the k_m factor is analytically described by coefficients that depend on the term β; see Eq. 40. These β-dependent coefficients are shown in Table 1. Besides the non-linear dependency that the coefficients show with β, as β itself is proportional to $\sqrt {\sigma _{m}}$, the load applied is further responsible for non-linear trends. Therefore, in order to understand the k_m non-linear trend shown in Figs. 12, 13 and 14, a focus on how the coefficients develop with the load variation is needed. This allows the study of k_m not to depend on the magnitude of the initial distortion.

Table 1 β-dependent coefficients

From the analytical point of view, under tension, the β-dependent coefficients converge to a single function $\left (1/\upbeta \right )$, which slowly decreases with an increasing load, as in Figs. 15 and 16. This function can well approximate the β-dependent coefficients for specific values of β, i.e. when the slenderness l/t and/or applied membrane stress are high. In fact, when $\upbeta >1\rightarrow \tanh {\upbeta }\rightarrow 1$, then the coefficients can be simplified as in Eqs. 56 and 57.

$$ \left[C1_{p};C1_{f}\right]\rightarrow\left( \frac{1}{\upbeta}\right) $$

(56)

$$ \left[C2_{p};C2_{f}\right]\rightarrow\left( \frac{\upbeta}{(\pi^{2}+{\upbeta}^{2})}\right)\approx\left( \frac{1}{\upbeta}\right)for\upbeta\gg\pi $$

(57)

For instance, this convergence exists when the applied tensile membrane stress is larger than 25 MPa for the slenderness l/t = 300. At a low load, the coefficients multiplying the amplitude of the initial curvature cannot neglect the π² at the denominator, so that the curvature effect is reduced much more by the straightening with respect to the lateral sway. Notice that for a membrane stress lower than 1 MPa, if β < 1, the above approximations are not valid. Actually, for β << 1, $\tanh {\upbeta }\rightarrow \upbeta$, so that the coefficients tend to the values shown in Eq. 58.

$$ \begin{array}{@{}rcl@{}} &&C1_{p}\rightarrow1 \qquad\qquad C1_{f}\rightarrow\frac{1}{2}\\ &&C2_{p}\rightarrow0 \qquad\qquad C2_{f}\rightarrow\frac{2}{\pi^{2}} \end{array} $$

(58)

Regarding the compression loading condition, the β-dependent coefficients $C1_{p}^{-}$, C2p⁻ and $C1_{f}^{-}$ diverge to $+\infty$ or $-\infty$, depending on the state of the stress experienced at the top surface of the beam before buckling instability is reached. The divergence occurs when the argument of $\tan (x)$ reaches π/2, as those coefficients are directly proportional to $\tan (x)$; see Table 1. $C2_{f}^{-}$ slowly approaches 0, being $C2_{f}^{-}\propto \frac {1}{\tan (x)}$.

Fig. 15

The β-dependent coefficients as a function of the applied tensile membrane stress σ_m.l/t = 300

Fig. 16

The β-dependent coefficients as a function of the applied tensile and compressive membrane stress σ_m. l/t = 42

The convergence trends explained above are visible in Figs. 15 and 16. The figures present the coefficients as a function of the applied nominal load σ_m for slenderness ratios of 42 and 300, respectively. The latter only studies tension loading conditions, as very high slenderness does not allow for meaningful studies under compression. As is observable from the figures and from the analytical approximations, under tension loading, pinned and fixed BCs result in different stress coefficients for β < 1. Since β depends on both the slenderness ratio l/t and the applied stress σ_m, it is noticeable that for high slenderness, the effect of the boundary conditions already becomes negligible around 5 MPa, and the convergence between first- (C1_x) and second-order (C2_x) terms occurs at very low tension loading (i.e. around 10 MPa), while for l/t = 42 these behaviours happen above 50 MPa. In general, an increased tension loading condition is beneficial for the distorted beam, if limited within its elastic strain field. In compression, BCs visibly affect the structural stress when the nominal applied load is not approaching the buckling limit (around − 97 and − 24 MPa for fixed and pinned beams, respectively).

4.3 Influence of the slenderness on β-dependent coefficients

Figures 17 and 18 present the β-dependent coefficient profiles as a function of the slenderness l/t (varying from 20 to 300) for unitary applied tension and compression. The analytical considerations about the approximation of the coefficients for β < 1 and β > 1 hold in this case, as well, as the term β is directly proportional to l/t. The function 1/β is also plotted in Fig. 17, where it is pointed out that, under a low load, such an approximation is valid only for the C1_p coefficient and high slenderness ratios. In tension, the difference between the coefficients is reduced by increased slenderness, meaning that the beam becomes more sensitive to the straightening effect as its slenderness increases. Considering that an increased load would only shrink the vertical axis, for very slender beams, the straightening effect is likely to dominate over the initial distortion, regardless of its magnitude and topology. An exception is the trend assumed by C2_p, which increases with the slenderness from a zero starting position. This indicates that a curved, non-slender, pinned beam is not noticeably affected by the amplitude of the initial curvature, which starts actually worsening the stress state when l/t > 180. An additional effect resulting from increased slenderness is that the influence of the BCs is considerably reduced: from a difference of 50% at l/t = 20, C1_p and C1_f end up at a 10% gap at l/t = 300. Similarly, the percentage difference between C2_p and C2_f is around 80%.

Fig. 17

The β-dependent coefficients as a function of slenderness. Tension load (1 MPa)

Fig. 18

The β-dependent coefficients as a function of slenderness. Compression load (− 1 MPa)

Figure 18 for compression points out the early buckling experienced by slender beams: a pinned beam does not withstand − 1 MPa compression if its slenderness overcomes 180; the fixed beam is stiffer overall, but even a slightly higher load would cause $C1_{f}^{-}$ to diverge fast.

4.4 Influence of the curvature on the k_m factor

The influence of the curvature, i.e. the ratio of the angles, is studied for tension and compression loading conditions. The study considers a fixed amplitude for the global angle α_G, so as to highlight the effect of having a curvature (i.e. a local angle α_L) for the initial shape of the beam.

From the analytical point of view, according to Eqs. 6, 41 and 45 can be written as in Eqs. 59 and 60, respectively. As it is known that $\tan (x)\rightarrow x$ and α_L = (α_L/α_G) ⋅ α_G, the formulations become linear functions of the local angle for a given global angle, applied stress and structure dimensions. For the sake of simplicity, the β-dependent coefficients are not given in expanded form.

$$ \begin{array}{@{}rcl@{}} \textit{Fixed end:}&& k_{m}=1+6\tan(\alpha_{G})\frac{l}{t}C1_{f}+6(\tan(\alpha_{L})-\tan(\alpha_{G}))\frac{l}{t}C2_{f}\\ &&\rightarrow k_{m}=1+6\alpha_{G}\frac{l}{t}(C1_{f}-C2_{f})+6(\alpha_{L})\frac{l}{t}C2_{f} \end{array} $$

(59)

$$ \begin{array}{@{}rcl@{}} {Pinned~end:}&& k_{m}=1+6\tan(\alpha_{G})\frac{l}{t}C1_{p}+6(\tan(\alpha_{L})-\tan(\alpha_{G}))\frac{l}{t}C2_{p}\\ &&\rightarrow k_{m}=1+6\alpha_{G}\frac{l}{t}(C1_{p}-C2_{p})+6(\alpha_{L})\frac{l}{t}C2_{p} \end{array} $$

(60)

For compression loading, to understand the (k_m vs α_L/α_G) relationship, the k_m factor formulations (see Eqs. 49 and 50) can be expressed as functions of the angles, as shown for the tensile case in Eqs. 59 and 60. In this case, the β-dependent coefficients would be the ones indicated as $C1_{f}^{-}$, $C2_{f}^{-}$, $C1_{p}^{-}$ and $C2_{p}^{-}$.

In Fig. 19, the k_m factor is plotted with a varying angle ratio α_L/α_G under unitary tension. Results related to slenderness ratios of 42 (on the left) and 300, for both the beam models, are considered. It stands out that increasing the slenderness results in overall larger slopes and initial values at a null local angle, while an increase in stress would cause an effective reduction of the β-dependent coefficients (see Figs. 16 and 15), thus lowering both the slope and the k_m range in Fig. 19. The figure describes a positive growth of the k_m factor for higher angle ratios. A strong increase of l/t implies greater sensitivity to the onset of the initial curvature, which graphically corresponds to steeper slopes (the slope coefficients are < 1 for l/t = 42 and > 1 for l/t = 300). A difference between boundary conditions is also clearly visible in Fig. 20. Regardless of the slenderness, when the distorted beam remains flat (i.e. α_L/α_G = 1), the pinned boundary condition results in a slightly higher stress concentration until an angle ratio of about 3 is reached. This means that in the absence of curvature, the pinned end gives less stiff behaviour, while the fixed end provides better resistance to secondary bending effects. However, the presence of the curvature implies higher reacting moments for the fixed beam (i.e. higher Hot-Spot structural stress), which starts to experience larger deformation as soon as the local angle is big enough to dominate over the global one in terms of secondary bending moments. This explains the steeper slope observed for the fixed beam. Analytically, recalling the behaviour of the β-dependent coefficients, it is always true that C1_p > C1_f and C2_f > C2p. Therefore, looking at Eqs. 59 and 60, if the local angle is null, the estimated k_m for the pinned beam is greater than the other case, as (C1_p − C2_p) > (C1_f − C2f). Nevertheless, with larger slope coefficients, the fixed beam soon experiences higher stresses at the weld location.

Fig. 19

The stress magnification factor (k_mvsα_L/α_G) as a function of the angle ratio. Tension load (1 MPa)

Fig. 20

The stress magnification factor (k_mvsα_L/α_G) as a function of the angle ratio. Compression load (− 1 MPa)

In Fig. 20, the k_m factor is plotted with varying angle ratios α_L/α_G under unitary compression. The results relate to slenderness ratios of 42 and 150 for both the beam models. Higher l/t values are not meaningful cases under compression. Under compression (see Fig. 20), the slenderness impact is the same as that observed in tension. The slope and the initial value of the k_m factor increase for a slender beam. However, the slope related to the pinned-end configuration is negative, indicating that the onset of the initial curvature modifies the distortion mechanism of the top surface of the pinned beam. Moreover, when l/t = 150, such a slope is larger than the one for the fixed-end beam. Physically, this means that a slender fixed beam is less prone to buckling, and thus to secondary bending effects under compression (i.e. it is stiffer), than a slender pinned beam.

5 Discussion

The present investigation was focused on an analytical derivation of stress magnification factors to extend the existing design formulations for plate welding-induced angular misalignment (see, e.g. [9]) to the evaluation of the curvature effect. The structure took into account a geometrical non-linearity, and it was limited to small strains and moderate rotations, i.e. the von Kármán assumption was utilised. Thus, the beam slope was assumed to be below 5°, i.e. the curvature was approximated as the deflection second derivative $w^{\prime \prime }$. In the rest of the formulation, the Euler-Bernoulli beam theory, valid for thin-beams (l/t > 10), was utilised. The derivation was carried out by superimposing linear and trigonometric displacement fields to derive the strains, stresses, stress resultants and the equilibrium equations. This process maintains the existing design formulations and introduces the curvature effect to them through summation. As end flexibility can be included into the derivation in terms of fixity factors [20], it can be used to model various angular boundary conditions present in thin-walled structures. The transparency of the formulation allows the ease of further developments, e.g. for higher deformations and thicker beams with different kinematics. The theory was validated with geometrical non-linear finite element analyses and showed to have excellent agreement with them. The comparison with other analytical formulations, recently published by Zhou et al. [5] and Shen et al. [14], is now presented. The main difference between the present work and these two is in the modelling of the curvature shape and in the solutions methods.

Shen et al. [14] has developed a solution based on a polynomial quadratic function. In their solution, the effects of linear lateral sway and curvature (i.e. global and local angles) are coupled. Zhou et al. [5] modelled the curvature effect by using notional (i.e. dummy) loads on an ideal, straight beam, and describing the curvature with the slopes at the beam ends. This allows to present a versatile solution in terms of curvature shape, but it also implies the coupling of global and local effects. Differently, in the present formulation, the utilisation of the superposition principle and the modelling of a half-sine shape allow to decouple the global angular misalignment from the curvature effect. This makes the use of design equation easier, as we simply impose an additional term to the exiting k_m formulations. The basis of our formulation, i.e. the trigonometric description of the shape, originates from the ultimate strength assessment of thin-walled structures [22,23,24], in which the modelling of the von Kármán strains through a trigonometric series is a common approach. This series type of solution is also extendable for more complicated initial deformation shapes. These three different formulations also have differences in the resulting k_m factors.

Figure 21 shows the compared results under (a) compression and (b) tension load for a curved small-scale specimen (l/t = 42, with t = 3 mm) with clamped boundary conditions. The present formulation is referred to as k_{m, loc}. Although the formulations are applied for the same global and local angular misalignment, the k_m factor by [5] and the present solution show a difference, which is also due to the respective solution methods. In fact, the modelling by dummy loads utilised by Zhou et al. [5] leads to a solution composed by few additional terms with respect to the present solution. Nevertheless, the percentage difference is under 5% in compression and gradually increases under tension, but staying below 7%, for increasing load. While these two formulations well estimate the FEA results in compression up to around the 80% of the buckling load of the structure (i.e. $\sim -97$ MPa), the k_m factor by [14] generally differs from the others by more than 10%. On the contrary, under tension load, it slowly converges toward the solution presented by Zhou et al. [5], but the difference with k_{m, loc} remains around the 10%. In this case, the present model only differs in the particular solution of the ODE of motion that assumes the form of the imposed initial shape. Notice that the FEA results are exactly estimated by the present analytical model, but the disagreement with respect to the other models is clearly due to the said differences. If the slenderness ratio is increased to 300, as shown in Fig. 22, the k_m factor by Shen et al. [14] and the present solution differ less than 5% once the tension load is higher than 45 MPa (i.e. $\sim 12\%$ of the yielding strength). In the same figure, a percentage difference < 5% between k_{m, loc} and the formulation by [5] occurs around 140 MPa (i.e. $\sim 40\%$).

Fig. 21

Comparison between the present analytical model and the formulations provided in [5] and [14]. a Stress magnification factor as a function of the compression load percentage with respect to the buckling load (k_mvsσ_m/σ_cr) and b as function of the tension load percentage with respect to the yielding strength (k_mvsσ_m/σ_y). FEA solutions from this study are plotted. l/t = 42 and $\alpha _{L}/\alpha _{G}\sim 5$

Fig. 22

Comparison between the present analytical model and the formulations provided in [5] and [14]. Stress magnification factor as function of the tension load percentage with respect to the yielding strength (k_mvsσ_m/σ_y). l/t = 300 and $\alpha _{L}/\alpha _{G}\sim 5$

The previous comparison justifies the choice of limiting the analytical derivation for the improved k_m factor estimation to a half-sine curvature that led to a reliable analytical solution in which the global and local angular misalignment effects are clearly decoupled. As shown in Section 3, this simplicity in the formulation allows for a systematic sensitivity analysis, which brings up the role of each involved parameter. Furthermore, the derived analytical solution is similar to the analytical factor for angular misalignment between flat plates (i.e. k_{m, glob}). The flat plate solution is extended by a second-order term to consider the curvature for both pinned and fixed BCs; see k_{m, loc} in Table 2. The same holds in compression, if the k_{m, glob} formulations are modified with the same approach followed in Section 2.7, i.e. by using the definitions in Eq. 48. The flat and curved plate solutions that are compared rely on the same basics, which include the initial distortion and the developing deflection into the beam equilibrium. However, the k_{m, glob} formulations are not intended to describe the onset of a local angular misalignment as a result of a curved shape. Referring to the formulations derived for tension loads, as the β-dependent coefficients are always positive (see Figs. 15 and 16), it is evident that the k_{m, glob} results in an underestimation of the structural stress for curved shapes, if α = α_G as by definition. In fact, the term that accounts for the initial curvature is missing (see the framed terms in Table 2), meaning that the angle portion $\alpha _{a_{0}}$ defined in Eq. 7 is not included in k_{m, glob}. This underestimation is expected to diminish for a small amplitude of the initial curvature and when the β-dependent coefficients C2_{f, p} become smaller, i.e. for an increasing straightening effect. As observed in Sections 4.2, this happens at high loading conditions, especially for very slender beams.

Table 2 Compared k_{m, angular} factor formulations for tension loading condition

In order to understand to what extent the local angular misalignment and the load that is applied make the k_{m, glob} formulations unsuitable, the relative percent difference, or error, between the two analytical approaches is reported as a function of the angle ratio for slendernesses of 300, 42 and 20; see, respectively, Figs. 23, 24 and 25. The relative error is computed as e = (k_{m, loc} − k_{m, glob})/k_{m, loc}%. In the figure, the data refers to distorted beams with $\alpha _{G}\sim 0,24$ and $\alpha _{G}\sim 2$° for slenderness ratios of 300 and 42, respectively. Both these angles correspond to about a 5-mm-high lateral sway y₀. For l/t = 20 the global angle is kept to ∼2°, as for l/t = 42, assuming that only the thickness increases up to ∼6 mm. Figures 23 and 24 show that whenever the amplitude of the initial curvature a₀ ≠ 0 (i.e. α_L/α_G ≠ 1), k_{m, glob} cannot provide reliable results either for (a) fixed or (b) pinned boundary conditions. In fact, the percent error shows a very steep increase even at small angle ratios. Despite the straightening effect, at high loading conditions, k_{m, glob} still considerably underestimates the stress magnification factor evaluated by using the derived k_m factors which have been validated for curved shapes; with a tension load of 300 MPa, e > ∼ 12% when the angle ratio is equal to 2 for both fixed and pinned configurations. This suggests that, regardless of the load applied and the slenderness ratio, if the initial curvature implies a non-negligible local angular misalignment, the k_{m, glob} formulations need to be extended to higher-order deformation shapes, i.e. curved shapes. An exception can be made for a pinned beam under a very low load; (see Figs. 24 and 25). This depends on the trend seen for the coefficient C2_{f, p} in Fig. 17.

Fig. 23

Percent error plotted as a function of the angle ratio (evsα_L/α_G) for a fixed and b pinned boundary conditions under tension load. L/t = 300 and initial lateral sway y₀ = 5 mm

Fig. 24

Percent error plotted as a function of the angle ratio (evsα_L/α_G) for a fixed and b pinned boundary conditions under tension load. L/t = 42 and initial lateral sway y₀ = 5 mm

Fig. 25

Percent error plotted as a function of the angle ratio (evsα_L/α_G) for a fixed and b pinned boundary conditions under tension load. L/t = 20 and initial lateral sway y₀ = 5 mm

Figures 26 and 27 show the percent error in the k_m estimation using k_{m, glob}, for the compression loading condition applied to (a) fixed and (b) pinned beams with initial distortion. Slenderness ratios of 42 and 20 and $\alpha _{G}\sim 2$° are considered. Also in this case, the k_{m, glob} formulations result unsuitable for the stress assessment of initially curved shapes. The impact of the local angular misalignment on the fixed beam is similar to the one observed for the tension loading condition, i.e. k_{m, glob} greatly underestimates the structural stress. The error overcomes 20% already under − 1 MPa and with an angle ratio lower than 2. In both figures, the (a) fixed BCs show overlapping of the errors related to − 1, − 5 and − 10 MPa, while increasing the load to − 20 MPa results in reduced e values. The reason is that, when approaching the buckling load, both the formulations diverge to +∞ and become closer to each other. However, this is not relevant, as the computed error at a high compression load remains unacceptable for engineering purposes. It can be concluded that, for fixed BCs, it is not possible to neglect the presence of the curvature shape. Differently, in Figs. 26b and 27b, for the curved pinned beam, the k_{m, glob} formulation ends up overestimating the stress magnification factor based on the local angular misalignment. This occurs because the change in the mechanical behaviour as a result of a pronounced local angular misalignment (see Section 4.1) cannot be described by k_{m, glob}. In fact, this trend is analytically related to the coefficient $C2_{p}^{-}$ (see Eq. 54), which is missing in the flat plate solution. Nevertheless, under a very low compression load (i.e. − (1 − 5) MPa) the overestimation remains below 10% for l/t = 42, meaning that the local angle does not visibly affect the stress concentration at the weld location, and both the formulations can be applied to estimate the stress magnification factor at the weld location. Analytically, this depends on the $C2_{p}^{-}$ coefficient trend, which is close to 0 at a low compression load (i.e. soon after a change in the mechanical behaviour of the beam); see Fig. 16. As the slenderness ratio is reduced to 20, the relevance of the initial curvature effect on a pinned beam is greatly reduced and considerable errors occur only for pronounced local angles (e.g. $\alpha _{L}/\alpha _{G}\sim 5$), which, however, are not likely to set on thicker and non-slender components.

Fig. 26

Percent error plotted as a function of the angle ratio (evsα_L/α_G) for a fixed and b pinned boundary conditions under compression load. L/t = 42 and lateral sway y₀ = 5 mm

Fig. 27

Percent error plotted as a function of the angle ratio (evsα_L/α_G) for a fixed and b pinned boundary conditions under compression load. L/t = 20 and initial lateral sway y₀ = 5 mm

Based on this comparison, whenever the initial distortion includes a curvature, the fatigue assessment requires the consideration of the non-linear geometry, with an exception for pinned beams under low compression loads.

6 Conclusion

This study presented new analytical formulations for estimating the stress magnification factors k_m resulting from the angular misalignment under axial load, in which the global effect is decoupled from the local effect of a curved distortion shape. Based on the von Kármán assumption applied to an Euler-Bernoulli beam, the analytical derivation considered the curvature effect by linear superposition. The formulations extend the existing solutions for flat plates by including an additional term that accounts for the local angular misalignment. The theory was validated with geometrical non-linear finite element analysis for pinned and fixed BCs. Based on the present study, the following conslusions can be drawn below.

The von Kármán assumption can properly describe the secondary bending effect on curved plates. The use of a half-sine deformation shape, the superposition principle and the slope deflection method lead to concise formulations, which are valid (i.e. under 2% error) as long as the component does not approach plasticity, i.e. within its yielding strength and the 80% of its buckling limit.

The local angular misalignment α_L considerably affects the response of the structure. The significance range (i.e. with error > 10%) of the formulations that are presented with respect to the flat plate solutions k_{m, glob}, requires that angle ratio α_L/α_G > 1.75 in case of high slenderness and tension load. At low load, the angle ratio already becomes relevant at around α_L/α_G = 1.25. With reduced slenderness, the k_{m, glob} formulations should not be applied for curved plates, except when pinned BCs are assumed, and the load is low (i.e. about from − 5 to 1 MPa).

The non-linear relationship between k_m and the nominal stress σ_m that is applied is evaluated by coefficients that are non-linear in β (with β ∝ l/t and $\upbeta \propto \sqrt {\sigma _{m}}$). Under tension, these coefficients describe the straightening effect, which significantly benefits the effective fatigue strength, especially for very slender structures. Although a high tension load cannot fully recover the detrimental effect due to the curvature, it makes the lateral sway and the BCs effects negligible. On the contrary, under increasing compression load, the BCs effect matters and the structure undergoes increased structural stress, i.e. reduced fatigue strength. Differently than the existing formulations, the coefficients can also describe a change in the response of the beam, when the compression applied turns into a tension stress-state for the top surface.

Despite the improvement obtained on the existing flat plate solutions, some aspects that may considerably affect the state of stress of a welded thin plate in a stiffened panel are still neglected. Thereby, although the half-sine shaped 1D beam is a reliable idealisation for small-scale specimens, further studies are needed to assess the engineering relevance of the analytical model for full-scale, thin-walled stiffened panels. Specifically, these structures require the consideration of non-ideal rigidity of the BCs. Furthermore, to enable an exact estimation until the buckling instability, the assumption that the slope generally stays below 5° should be relaxed. An additional improvement would bring the study to the consideration of the in-plane stress redistribution over the plate, which results from the shear effects and the influence of the whole stiffening frame of the panel.

Appendix: Buckling limit computation

In compression, the loading condition is limited to the buckling limits (i.e. the Euler loads) of the fixed and pinned-end beams. From the literature (e.g. [17, 18]), the Euler load is defined as in Eq. 61.

$$ P_{cr}=\left( \frac{\pi}{Kl}\right)^{2}EI, $$

(61)

where K is a coefficient that depends on the BCs. For the specific condition in this study, the fixed end requires K = 1, while K = 2 is applied for the cantilever beam. In Eq. 61, E is the modulus of elasticity of the material, I is the principal moment of inertia of the beam, defined as I = bt³/12 for rectangular sections, and l is the beam length. The same buckling limits are also obtainable by analytical computation from Eqs. 49 and 50 by imposing β/2 and β equal to π/2, respectively (see Eqs. 62 and 63). In fact, this causes the tangent function to diverge to +∞, thus describing the unstable condition of the beam under a compression load.

$$ \frac{\upbeta}{2}=\frac{\pi}{2}\Rightarrow P_{cr}=\left( \frac{\pi t}{2l}\right)^{2}\frac{Ebt}{3} $$

(62)

$$ \upbeta=\frac{\pi}{2}\Rightarrow P_{cr}=\left( \frac{\pi t}{4l}\right)^{2}\frac{Ebt}{3} $$

(63)

In the above equations, the term β is related to the applied axial load by the expression:

$$ \upbeta=\frac{2l}{t}\sqrt{\frac{3P}{Ebt}}, $$

(64)

where t is the beam thickness and b its width. Considering a beam 3-mm-thick model with l = 125 and b = 20 mm, and selecting a linear elastic material with a modulus of elasticity E = 206.8 GPa, the critical stress (σ_cr = P_cr/A) is ∼ (−97) and ∼ (−24) MPa for a fixed and pinned-end beam, respectively.