1 Introduction

Welding is one of the most common joining methods in steel construction. Metal active gas (MAG) together with metal inert gas (MIG) welding processes currently accounts for 70 to 80% of all manual and robot welding [1]. Additional deformations and residual stresses are produced during welding processes. The welding deformations caused by the shrinkage of filler material can be divided into several types. Transverse shrinkage and angular distortion are caused by shrinkage perpendicular to the weld bead. For a long butt weld, rotational distortion led by this transverse shrinkage may occur. Longitudinal shrinkage, longitudinal distortion, and buckling are due to shrinkage along the weld bead. The welding residual stresses result from the restraints of adjacent base metal during the shrinkage of melted metal.

The welding deformations and residual stresses in a structure may influence the functionality, safety, and durability. Thus, it is of significant importance to reduce adverse deformation and residual stresses. Traditionally, trial and error tests are used to solve these problems. Their drawbacks are that they are time-consuming and expensive. Nowadays, digital tools involving FE simulations and databases possess of great potential to reduce the lead times of new developments by replacing the physical test loop [2]. One aspect of the digitalised welding process is to use computational welding mechanics (CWM) methods to estimate the mechanical response of welded structures.

A number of computational welding mechanics (CWM) methods have been developed over the last few decades. Most studies have been carried out regarding the thermo-elastic-plastic method [3,4,5,6,7,8] which is a coupled thermal and mechanical FE simulation. The thermo-elastic-plastic method has been applied to different types of small welded structures such as butt welds [3], fillet welds [4], and overlap welds [5]. Due to the high level of computational time necessary, some simplified thermo-elastic-plastic approaches have been applied such as block-dumping [6] and substructuring [7, 8]. The substructuring method shows good estimation ability as concerns deformations [8] and residual stresses [7].

In addition to thermo-elastic-plastic method, there is another method entitled the inherent strain method. The concept of inherent strain was developed by Ueda et al. in 1975 [9] and many research work has been carried out based on this concept. In 1983, Ueda et al. [10] utilized inherent strain to measure the residual stresses in long welded joints. From 1989 to 1996, the estimation of residual stresses was developed by using inherent strain in butt welds, T-type fillet welds, and long welds [11,12,13,14]. In 1997, Luo et al. [15] applied inherent strain calculated from the thermo-elastic-plastic method where the constraints at each node were defined to calculate welding deformations and residual stresses. Souloumiac et al. [16] came up with the method called the local-global approach to calculating weld deformations where plastic strains calculated from a local 3D model by the thermo-elastic-plastic method were applied as initial strains in the elastic calculation of entire structure. In 2007, Deng et al. [17] developed an elastic finite element method called inherent deformation. In 2012, Khurram et al. [18] investigated an efficient FE technique using equivalent shrinkage force to predict welding deformations and residual stresses in butt joints. Barsoum et al. [19] compared the inherent strain [15], inherent deformation [17], and shrinkage force [18] methods to predict weld distortion of T-type fillet welds and they concluded that the inherent strain method was better than other two methods for angular distortion estimation and inherent deformation and shrinkage force methods are more suitable for estimating longitudinal and transverse shrinkage.

In this study, the following FE simulation methods: thermo-elastic-plastic [3,4,5], inherent strain (local-global) [16], and substructuring [7, 8] have been implemented both on T-type fillet weld and butt weld specimens to estimate angular distortion and residual stresses. The simulations using these methods have been performed using commercial software: Virfac ® 1.4.3.4 [20]. Through the validation of these methods by the experiments and by comparison, the application of digitalisation in welding can be boosted which leads to the reduction of trial and error tests and saves resources (money, time, material, etc.) accordingly. Moreover, in the inherent strain (local-global) method, several studies [21, 22] contributed to the setup of the size and boundary of the local model. Based on their work, the influence of the block length representing the activation of plastic strain in each time step and welding speed on angular distortion is also discussed.

2 Computational welding mechanics methods

2.1 Inherent strain (local-global)

The inherent strain (local-global) method needs plastic strains calculated from a local 3D model with thermo-elastic-plastic method as input. Afterwards, the elastic FEM analysis of the global model is carried out. Thus, the definition of the local model is very important. The influence of the local boundary condition has been highlighted by Souloumiac [16]. The boundary condition of the local model should be close to reality [21]. Duan et al. [22] developed a well-defined method of determining the size and boundary condition of local models. They concluded the local model size should be able to retain the same temperature history as the global model. The concept of “rigid border” boundary condition was defined by using a rigid part added to the frontier of the local model to keep the boundary in plane. In order to represent the mechanical conditions imposed by the rest of the structure, the rigidity of the rigid part may be changed by adjusting the value of Young’s modulus. In this study, the local model size and local boundary condition are defined according to Duan’s work [22].

2.2 Substructuring

The simulation model using the substructuring technique is performed by dividing the entire structure into two parts: the linear region and the nonlinear region. The elastic isotropic material model is assigned to the linear region with almost elastic behavior during the welding process. The elastic-plastic material model, assuming isotropic hardening, is applied to the nonlinear region which is close to the heat source.

3 T-type fillet welds

3.1 Experiments

Bhatti et al. [23] carried out comprehensive simulation work on angular distortion and residual stresses in T-type fillet welds in S355, S700, and S960 steels. In this study, the welding parameters, experimental setups, part of material model, and experimental measurements described in [23] are applied. Figure 1 shows a schematic illustration of the geometry of the specimen, the experimental setup, and the measuring locations. The welding parameters are listed in Table 1.

Fig. 1
figure 1

Schematic illustration of T-type fillet weld

Full size image
Table 1 Welding parameters
Full size table

3.2 Finite element model

3.2.1 Material modeling

The base plate and filler material are assumed to have the same material properties in the following numerical simulation methods: the thermo-elastic-plastic on the global model, the local model in inherent strain (local-global) method, and the nonlinear region in substructuring method. A J2-type isotropic hardening law [24] without considering phase transformation has been applied to the base plate and filler material. The relationship between the stress and strain of the material is shown in Eq. (1).

$$ \sigma ={\sigma}_y+H{\left({\varepsilon}^p\right)}^N $$
(1)

where σ is the total stress, σy is the initial yield stress, H is the hardening law coefficient, εp is the plastic strain, and N is the hardening law exponent.

JMat Pro® [25] has been used to simulate the flow stress of the material. The input chemical composition is based on typical values provided by Swedish Steel AB (SSAB). The temperature-dependent initial yield stress, hardening law coefficient, and hardening law exponent are calculated from the flow stress under the strain rate of 0.1 s−1 by using Eq. (1) (see Fig. 2c). The temperature-dependent thermal expansion, thermal conductivity, heat capacity, and Young’s modulus for S355 below 1500 °C are from [23], as seen in Fig. 2a and b. Artificial thermal conductivity has been induced to consider the heat transfer in the melting weld pool, which is assumed to be 300 W/(m°C) at 2000 °C [26]. Density and Poisson ratio are independent of temperature with the value of 7840 kg/m3 and 0.29 respectively [23].

Fig. 2
figure 2

Temperature-dependent material properties of S355. a Thermal conductivity and heat capacity. b Young’s modulus and thermal expansion [23]. c Initial yield stress, hardening law coefficient, and hardening law exponent

Full size image

The elastic isotropic material model is assigned to the linear region in the substructuring method (see Fig. 3a) and global model in the inherent strain (local-global) method. The parameters of the elastic isotropic material model are listed in Table 2.

Fig. 3
figure 3

a Linear and nonlinear regions in substructuring method. b Local model in inherent strain (local-global) method. c Boundary condition of local model

Full size image
Table 2 Elastic isotropic material model
Full size table

3.2.2 Heat source modeling

The heat source has been modeled as a cylindrical shape applying a constant heat density to the weld bead. The radial dimensions of the heat source in front, behind, and to the side are equal to the radius 푟. The energy of heat source Q (Joule/s) is expressed in Eq. (2)

$$ Q={\eta}_{\mathrm{arc}}\bullet U\bullet I $$
(2)

where ηarc is the arc efficiency, U is the voltage, and I is the current.

The radius of heat source and arc efficiency have been tuned according to the temperature histories at the points A and B described in [23]. The convection is set to 20 W/m2 °C corresponding to a still air environment. The temperature histories from the case where arc efficiency is 85% and the radius of cylindrical shape heat source is 4.24 mm shows good agreement (see Fig. 4a and b).

Fig. 4
figure 4

Temperature histories. a Point A. b Point B

Full size image

3.2.3 Boundary condition and mesh

In this study, the size of the local model can be seen in Fig. 3b which has the same temperature history curve as those in Fig. 4. In order to maintain the rigidity of the rigid part close to reality, the value of Young’s modulus applied to the rigid part is studied. Young’s modulus of the rigid part on the fixture side is set to 200 GPa to represent the effect of rigid clamping. Young’s modulus of the rigid part on the free edge of the base plate is set to 0.2 GPa to represent the constraints from the rest of the structure.

In order to achieve mesh independent results, mesh independency was also studied. The angular distortion was compared under three different meshes with element sizes 0.5, 1, and 2 mm, respectively. Under mesh size 0.5 and 1 mm, no obvious difference in angular distortion was observed. Thus, the minimum element length is defined as 1 mm. The fine mesh is applied in and around welds and the coarse mesh on the rest of the part. The total number of elements is 160,000.

3.3 Comparison

The estimated angular deflections using thermo-elastic-plastic, inherent strain (local-global), and substructuring methods are almost the same (see Fig. 5a). These methods underestimate the angular deflection by around 11% compared with the experimental measurement. Figure 5b and c show the comparison of experimental and estimated transverse residual stresses in front of the weld toe. The location of the measuring points is marked with red lines. The magnitude of tensile residual stresses calculated from the inherent strain (local-global) method is less than that of the thermo-elastic-plastic and substructuring methods and the stresses measured. Regarding computational time, using the inherent strain (local-global) method only takes a few minutes which does not include the time for thermo-elastic-plastic calculation on the local model. The computational time varies with the size of the local model. It took 4 h in this case. The computational time used was 8.5 h for the thermo-elastic-plastic method and 8 h for the substructuring method.

Fig. 5
figure 5

Estimation of angular distortion and residual stresses using thermo-elastic-plastic, inherent strain (local-global), and substructuring methods. a Angular distortion. b Transverse residual stresses on the left side. c Transverse residual stresses on the right side

Full size image

3.4 Influence of welding sequence

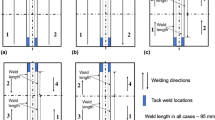
In order to study the influence of the welding sequence on distortion and residual stresses, four different welding sequence scenarios were selected in which the thermo-elastic-plastic and inherent strain (local-global) methods were applied (see Fig. 6). In the inherent strain (local-global) method, the plastic strains are from the thermo-elastic-plastic calculation on local models where the welding direction of passes are the same as those in the global model.

Fig. 6
figure 6

Welding sequence scenarios: a, b, c, d

Full size image

It is observed that for sequences 1 and 2, the difference between angular deflections estimated by the thermo-elastic-plastic method is 0.1 mm in Fig. 7. The same difference can be found between sequences 3 and 4. These results indicate that for T-type fillet welds, applying opposite welding directions for two passes results in less angular deflection than in the same welding direction. However, no difference can be seen between the deflections estimated by the inherent strain method (local-global) using different welding directions.

Fig. 7
figure 7

Comparison of angular distortion with different welding sequence by Themo-elastic-plastic and Inherent strain (local-global) method

Full size image

As can be seen in Fig. 7, the deflections estimated by the thermo-elastic-plastic method in sequences 1 and 2 are 0.09 mm smaller than those in sequences 3 and 4. Consequently, the case where the first weld pass is close to the rigid clamping boundary causes less deflection than the case where the first weld pass is close to the free edge. A greater difference (0.16 mm) can be found between the estimated deflections in these cases using the inherent strain (local-global) method compared with the thermo-elastic-plastic method. The inherent strain (local-global) method is able to estimate the difference of angular distortion caused by change of weld position with good accuracy.

In Fig. 8a and b, it can be seen that both estimated transverse residual stresses on the left side in sequences 1 and 2 are lower than those in sequences 3 and 4. The opposite situation can be observed on the right side. This proves that the position of weld pass does influence transverse residual stresses. The transverse residual stresses on the first weld pass side are lower than those on the second weld pass side. Any difference between the transverse residual stresses during different welding sequences estimated by the inherent strain (local-global) are not obvious.

Fig. 8
figure 8

Comparison of transverse residual stresses with different welding sequence: on the left (a, c) and right side (b, d) computed by Thermo-elastic-plastic (a, b) and Inherent strain (global-local) method (c, d)

Full size image

4 Butt welds

4.1 Experiments

4.1.1 Welding process

The butt weld specimen consisted of one backing plate (S355J2) and two base plates (S600MC) which were tack welded with a joint gap of 10 mm (see Fig. 9. The butt weld was produced manually using metal active gas (MAG) with the multi-pass process (2 passes). The welding parameters can be seen in Table 3. Three identical samples were manufactured. The deflection measurements from these samples were averaged.

Fig. 9
figure 9

Schematic illustration of butt weld specimen

Full size image
Table 3 Welding parameters of butt weld
Full size table

4.1.2 Temperature measurements

During the experiment, temperature data was collected using K-type thermocouples. Two holes with a diameter of 3 mm and a depth of 2 mm were drilled to insert the thermocouples which are 15 mm from the middle of weld bead, as shown in Fig. 9.

4.1.3 Residual stresses measurements

The residual stresses were measured using the X-ray diffraction method with Cr Kα radiation. Measurement line is approximately 14 mm away from the center line of the specimen, because of the drilled holes in the center line of the samples (see Fig. 9). The locations are ± 58 mm, ± 38 mm, ± 23 mm, ± 14 mm, ± 12 mm, ± 10 mm, and ± 8.5 mm, where zero position is the middle of the weld bead. The estimated penetration depth is 5 μm and the collimator size is 1 mm.

4.2 Finite element model

4.2.1 Material modeling

The base plates (S600MC) and filler material are modeled using J2-type isotropic hardening law with flow stress calculated from JMat Pro® (see Fig. 10c and d). Table 4 presents the typical chemical composition for base plates and filler material according to EN 10149-2 Standard and ASME SFA-5.20: E71T-12C-JH8. The other thermal and mechanical material properties of base plates and filler material are assumed to be the same as the material model of S700 from [23] without considering phase transformation (see Fig. 10a and b). The annealing temperature is set to be 1300 °C [27] to represent the effect of multi-pass weld. The material model of the backing plate is the same as the defined material model for S355. The elastic isotropic material model for base plates (S600MC) and filler material can be seen in Table 5. The material models are assigned to the different parts in Fig. 11, according to the description in the previous Section 3.2.1.

Fig. 10
figure 10

Temperature-dependent material properties of S600MC and filler material. a Thermal conductivity and heat capacity. b Young’s modulus and thermal expansion [23]. c Initial yield stress, hardening law coefficient, and hardening law exponent of S600MC. d Initial yield stress, hardening law coefficient, and hardening law exponent of filler material

Full size image
Table 4 Chemical composition for S600MC and filler material (% weight)
Full size table
Table 5 Elastic isotropic material model
Full size table
Fig. 11
figure 11

a Linear and nonlinear regions in substructuring method. b Local model in Inherent strain (local-global) method. c Boundary condition of local model

Full size image

4.2.2 Heat source modeling

A cylindrical shape with a 5-mm radius and 10-mm height has been modeled as the heat source for the first weld pass. The power density distribution is constant in the volume of the cylindrical heat source. For the second weld pass, the same heat source as in Section 3.2.2 is applied and the radius 푟 is set to 6.5 mm. The heat source efficiency is assumed to be 0.8 and the effective power for the first and second pass is 3388 W and 3509 W respectively using Eq. (2). The isothermal contour plots for the fusion zone, HAZ, and penetration profile show a good match with the macrographs for both weld passes (see Fig. 12a and b). In order to consider the heat sink effect on the bottom surface of the backing plate, a heat convection coefficient of 300 W/(m2 °C) was applied to the entire bottom surface of the backing plate [28]. Convection was set at a constant value of 20 W/m2°C corresponding to a still air environment on all surfaces except the bottom surface of the backing plate. The initial temperature was set at 34°C according to the measurements.

Fig. 12
figure 12

Heat source calibration. a Macrograph and isotherms for the first deposited pass. b Macrograph and isotherms for the second deposited pass. c Temperature histories at 15 mm from the weld center line

Full size image

The temperature histories from FEM simulation show good agreement with the measurements at 15 mm from the weld centre line (see Fig. 12c). The peak temperatures from FEM simulation for both passes are slightly lower than those measured.

4.2.3 Boundary condition and mesh

No external constraint was applied to the butt weld specimen during the manufacturing process. For the global model in the thermo-elastic-plastic, inherent strain (local-global), and substructuring methods, the rigid body motion was prevented. For the thermo-elastic-plastic simulation on the local model in the inherent strain (local-global) method, two rigid parts with Young’s modulus of 0.2 GPa were applied to both sides of the local model to represent the constraint effect from the rest of the structure (see Fig. 8c).

The length of elements in the weld beads were set at 1.5 mm for both passes. The coarse mesh was applied to the linear region. The total number of elements was 151,542.

4.3 Comparison

The estimated angular deflection from the thermo-elastic-plastic, inherent strain (local-global), and substructuring methods is − 3.7 mm, − 2.6 mm, and − 4.7 mm respectively (see Fig. 13a). In comparison to the experimental measurement (− 3.5 mm), the thermo-elastic-plastic method shows good agreement. The inherent strain (local-global) method underestimates the angular deflection by 26% and the substructuring method overestimates the angular deflection by 34%.

Fig. 13
figure 13

Estimation of angular distortion and residual stresses using thermo-elastic-plastic, inherent strain (local-global), and substructuring methods. a Angular distortion. b Transverse residual stresses on the left side. c Transverse residual stresses on the right side. d Longitudinal residual stresses on the left side. e Longitudinal residual stresses on the right side

Full size image

For transverse residual stresses, the trend is captured and relatively large differences can be observed between the estimated stresses from the thermo-elastic-plastic, inherent strain, and substructuring methods and the experimental measurements. In order to increase accuracy, phase transformation could be included in further studies.

The estimated longitudinal residual stresses from the thermo-elastic-plastic, inherent strain, and substructuring methods show good agreement with the measurements, as shown in Fig. 13d and e.

The computational time for the thermo-elastic-plastic, inherent strain (local-global), and substructuring methods are 18, 0.2, and 12 h respectively. The computational time for the thermo-elastic-plastic analysis on the local model is 10 h. The computational time for the substructuring method is 30% less than the thermo-elastic-plastic method.

5 Discussion

Although the inherent strain (local-global) method needs very little computational time, a certain level of underestimation can be observed between the estimated and measured angular deflection and residual stresses (see Figs. 5 and 10). This type of difference could be observed in [22] as well. In order to understand where this variation comes from, the influence of block length and welding speed on angular distortion will be discussed.

5.1 Influence of block length

In the inherent strain (local-global) method, the activation of plastic strain in the weld bead can be achieved in a single time step or divided into several time steps. The block length represents the method of activating the plastic strain.

As can be seen in Fig. 14, in both the T-type fillet weld and butt weld specimens, reducing the block length results in the increase of angular deflection. It is due to the reason that the activation of weld bead also provides the additional stiffness of the structure. For the T-type fillet weld specimen, the angular deflection increases by 2 mm when the block length changes from 130 to 16.25 mm. The level of accuracy is defined by the ratio of estimated and measured angular deflection. As can be seen, the inherent strain (local-global) method underestimates the angular deflection by about 17% with a block length of 130 mm and overestimates the angular deflection by around 14% with a block length of 16.25 mm. For the butt weld specimen, reducing the block length results in increasing the level of accuracy significantly which is from 37 to 91%.

Fig. 14
figure 14

Influence of the block length. a T-type fillet weld specimen. b Butt weld specimen

Full size image

5.2 Influence of welding speed

There is a difference between the welding speed of the T-type fillet weld (8.3 mm/s) and butt weld (1.38 mm/s for the first pass and 2.22 mm/s for the second pass). In order to include the influence of welding speed, a new parameter tb “block period” calculated by Eq. 3 is induced.

$$ {t}_b=\frac{l_b}{v} $$
(3)

where tb is the block period, lb is the length of block, and v is the welding speed.

In Fig. 15a, the level of accuracy is increased with the decrease of the block period and the curve trends for the T-type fillet weld and butt weld are similar. The overlap part of this line between block period 7 and 16 s indicates that the level of accuracy is independent of the type of weld. In addition, erroneous results could be observed when very short block period is applied as the plastic strain is extracted when the structure cools down to room temperature. It is suggested that an appropriate block period be taken into account in the inherent strain (local-global) method.

Fig. 15
figure 15

Influence of block period

Full size image

In the inherent strain (local-global) method in Section 3 and 4, the weld bead has been divided into two blocks for T-type fillet weld and four blocks for butt weld (see Fig. 16a and b). The level of accuracy is increased by 6% for T-type fillet weld specimen and 37% for butt weld specimen compared with the case where the plastic strain is activated in a single time step. Consequently, dividing the weld bead into an appropriate number of blocks and activating the plastic strain gradually can reduce the level of underestimation on angular distortion when using inherent strain (local-global) method.

Fig. 16
figure 16

Illustration of the block length and block period. a T-type fillet weld specimen. b Butt weld specimen

Full size image

The cooling time ∆t8/5 between 800 and 500 °C for the T-type fillet weld specimen is 5.6 s and for the butt weld specimen is about 15 s, according to Eq. 4 [29].

$$ \Delta {t}_{8/5}=\left(6700-5\bullet {T}_0\right)\bullet {\overline{q}}_w\bullet \left(\frac{1}{500-{T}_0}-\frac{1}{800-{T}_0}\right) $$
(4)

where ∆t8/5 is the cooling time between 800 and 500 ° C, T0 is the preheating temperature°C, and \( {\overline{q}}_w \) is the gross heat input per unit length of weld kJ/mm.

It is found that the cooling time ∆t8/5 for the butt weld is much higher than the one for the T-type fillet and values are similar to the block period applied to those two specimens. The cooling time ∆t8/5 is dependent on many factors such as heat input, plate thickness, joint type, and welding process [30] and could be utilized as a reference for the block period. In order to determine the appropriate block period in the inherent strain (local-global) method, the relationship between the stains in the weld and temperature history could be included in further studies.

5.3 Computational time and accuracy

As shown in Fig. 17, the accuracy and computational time of the thermo-elastic-plastic method are greater than the inherent strain (local-global) and substructuring methods. The substructuring method reduces computational time by 6 to 30% compared to the thermo-elastic-plastic method and has good accuracy of estimation. The inherent strain (local-global) method is very time-efficient when having plastic strains as input. Computational time of the thermo-elastic-plastic analysis on the local model is 4 h for the T-type fillet weld and 10 h for the butt weld, whereas the accuracy of the inherent strain (local-global) method is lower than the thermo-elastic-plastic and substructuring methods. In the case of applying the same plastic strains to the T-type fillet weld, the accuracy of estimated angular distortion is varied from 83 to 114%. The variation in the butt weld specimen is even greater ranging from 37 to 91.5%. The dotted line represents the variation of accuracy of estimated angular distortion. The reasons for these variations have been discussed in Sections 5.1 and 5.2.

Fig. 17
figure 17

Computational time and accuracy of the thermo-elastic-plastic, inherent strain, and substructuring methods. a T-type fillet weld specimen. b Butt weld specimen

Full size image

6 Conclusions

This study conducted the estimation of angular distortion and residual stresses on T-type fillet weld and butt weld specimens by applying the thermo-elastic-plastic, inherent strain (local-global), and substructuring methods. These methods are compared in terms of accuracy and computational time. The influence of the welding sequence on distortion and transverse residual stresses was studied numerically by implementing the thermo-elastic-plastic and inherent strain (local-global) methods on T-type fillet welds. Moreover, in order to achieve a better understanding of the variations in the inherent strain (local-global) method, the influence of block length and welding speed on angular distortion has been discussed. Conclusions are as follows:

  • The estimated angular distortion and residual stresses in front of the weld toe from the thermo-elastic-plastic, inherent strain (local-global), and substructuring methods are in good agreement with the experimental measurements of T-type fillet welds.

  • Substructuring method can reduce computational hours by up to 30% as compared to the thermo-elastic-plastic method. The inherent strain (local-global) method is very time-efficient compared with the others, but it needs plastic strains as input.

  • For the T-type fillet weld, the inherent strain (local-global) method is able to estimate the difference of angular distortion caused by change of weld position as predicted in the thermo-elastic-plastic method. No obvious difference in angular distortion under different weld directions is observed in the inherent strain (local-global) method; however, the thermo-elastic-plastic method captures the differences.

  • The transverse residual stresses of the T-type fillet weld on the side of first weld pass are lower than those on the other side according to numerical estimation using the thermo-elastic-plastic method. Such differences in transverse residual stresses is not observed in the inherent strain (local-global) method

  • For the inherent strain (local-global) method, the influence of block length on estimated angular distortion is significant. Reducing the block length results in an increased angular distortion and reduced level of underestimation.

  • Block period is introduced to consider the influence of welding speed together with block length on the estimation of angular distortion in the inherent strain (local-global) method. It is observed that the level of underestimation can be reduced with the decrease of block period. Consequently, it is suggested the weld bead with a large block period be divided into a number of blocks with an appropriate block period for each.