Introduction

The study of nanoclusters is an important subject of research due to their various applications in many fields [1–6]. By studying the properties of nanoclusters as a function of size, one hopes to learn how the bulk properties evolve and it can be providing important clues to the understanding of the mechanism of catalysis and other chemical properties [2, 3]. In both theoretical and experimental aspects, more studies on the clusters improve the processes of understanding their structures, electronic properties, and catalysis [4]. From experimental aspect, the development of laser vaporization technique has enabled experimentalists to produce and characterize atomic clusters of specific size and composition [2]. But synthesis of clusters is sometimes difficult because of (1) size selected clusters cannot be produced in sufficient quantities and (2) these are metastable, they would coalesce when brought in the vicinity of each other [2]. In addition, there is no experimental technique that can provide direct information on cluster geometry [2]. From theoretical aspect, on the other hand, geometry and many other properties of clusters have been successfully predicted and there are abundant reports in the literature that investigate the properties of clusters theoretically [7–11].

The aluminum nanoclusters have simple electronic structure and high electrical conductivity and, therefore, are important in catalytic processes such as hydrogenation and dehydrogenation reactions as well as fuel cell technology [12, 13]. In recent years, Al and Al-based nanoclusters are the subject of numerous experimental and theoretical studies [14–20]. The reaction of Al clusters, Al n (n = 7–24), formed by laser vaporization, with oxygen and ammonia has been studied using a fast flow reactor [14]. Reber et al. [15] have shown that some of the Al clusters are reactive toward even less reactive hydrocarbons. The interaction between Al clusters and several molecules such as H2O [4, 16], H2 [17, 18] NH2 [19] and O2 [20] was theoretically investigated.

Real catalysts mainly consist of a heterometallic or bimetallic system, which can enhance reactivity and selectivity [13]. Therefore, in theoretical study of clusters, much attention should be paid to the study of bimetallic clusters and their application in catalytic reactions. Al clusters are the most important lightweight materials for hydrogen adsorption and binding of hydrogen to the Al clusters can be significantly improved via doping. Kumar et al. [21] investigated the most stable structures and physical properties of Al12Si, Al18Si, and Al22Si clusters. They reported that Si impurity makes these clusters electronically closed shell and leads to a large gain in the binding energy. Majumder et al. [22] studied the equilibrium geometry and energetics of Si n and Si n−1Al clusters using a combination of the density functional theory and molecular dynamics simulation under the local spin density (LSD) approximation. Their results revealed that clusters with n = 4, 6, 10 show higher stability as compared to its neighboring clusters. Effect of aluminum impurity atoms on the structures and stabilities of neutral and ionic Si n (n = 2–21) clusters have been investigated using full-potential linear-muffin-tin-orbital molecular-dynamics [23]. They found that most of the ground-state structures for neutral and ionic Si n Al (n = 1–20) clusters can be obtained by substituting one Si atom of their corresponding Si clusters with an Al atom.

In this study, we performed a comprehensive and systematic DFT study on the properties of Al n (n = 1–13) and Al n Si m (n + m = 5–7) nanoclusters. Binding energy per atom, second-order difference of cluster energies, fragmentation energy, dipole moment (μ), Al–Al bond distance, and chemical hardness of nanoclusters were calculated and discussed. Variations of geometry, stability and reactivity of nanoclusters were also analyzed as a function of cluster size as well as cluster composition.

Computational methods

The geometry of all clusters including Al n (n = 1–13) and Al n Si m (n = 4–6, m = 1–3, n + m = 5–7) were optimized without any constraint using the functionals of Becke’ three-parameter hybrid exchange functional [24] and the Lee–Yang–Parr correlation functional [25] (B3LYP) and 6–31 + G* basis set. Effect of basis set was also studied on the electronic properties of most stable structures considering 6–31 + G** and 6–311 + G* basis sets. All calculations were done by the Gaussian03 package [26]. The B3LYP hybrid density functional has been used abundantly for the study of Al clusters. For example, B3LYP functional has been used for the study of structure and electronic properties of Al n As clusters [7]. Guo et al. [13] employed B3LYP functional to investigate the structure of Al n V clusters and their interaction with molecular hydrogen. Dissociation of hydrogen on small Al clusters has been studied through B3LYP functional [17]. In addition, all calculations involved the determination of vibrational frequencies at the same level of theory and basis set for the validation of the local energy minima of each optimized structure as well as zero point energy correction.

Results and discussion

Al n (n = 1–13) clusters

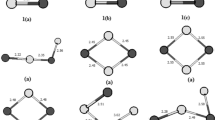
To find the most stable structure of Al n clusters we optimized each cluster, initiating with different possible structures as input file, at three spin multiplicities of, 1, 3, and 5 for clusters with even electrons number and 2, 4, and 6 for clusters with odd electrons number. Figure 1 presents the most stable structure of Aln clusters while the corresponding spin multiplicities (Ms) and dipole moments (μ) are summarized in Table 1. Other higher energy structures along with the corresponding spin multiplicities as well as relative energies (E r) are collected as supporting information in table S.1. The relative energies are calculated by subtracting the energy of the most stable structure from the energy of a structure in the series. The calculated vibrational frequencies of most stable structures of Al n clusters computed at B3LYP/6–31 + G* level of theory are collected as supporting information in table S.2. The structures reported in Fig. 1 are in agreement with those reported in the literature [2, 4, 7, 17]. It has been shown that for Al n clusters up to five atoms the structures are planar and for clusters containing 6–13 atoms the structures become three dimensional [2, 4, 7, 17]. For Al6 cluster we found that the most stable structure is trigonal prism geometry with Ms = 3 while the octahedral geometry with Ms = 1 is only 0.01 eV less stable. Pino et al. [17] obtained different geometries as the most stable structure of Al6 depending on the method used for optimization. With B3LYP they obtained trigonal prism geometry with Ms = 3 as the most stable structure while the octahedral geometry with Ms = 1 is only 0.006 eV less stable. With CCSD(T), on the other hand, they obtained octahedral geometry with Ms = 1 as the most stable structure while the trigonal prism geometry with Ms = 3 is 0.162 eV less stable. For Al13 cluster, we obtained distorted icosahedron geometry with Ms = 2 as the most stable structure in agreement with some reported results [2, 7]. Some authors reported regular icosahedron geometry (Ih symmetry) as the most stable structure for Al13 cluster [4, 12].

Fig. 1
figure 1

The most stable structures of Al n (n = 2–13) clusters computed at B3LYP/6–31 + G* level of theory

Full size image
Table 1 The spin multiplicity and dipole moment of most stable Al n clusters presented in Fig. 1
Full size table

According to the results of Table 1 the doublet spin state is the lowest in energy (most stable state) for all Al n clusters with odd number of atoms. For Al n clusters with even number of atoms, on the other hand, the triplet spin state is the lowest in energy for Al2, Al4, Al6 and the singlet spin state is the lowest in energy for Al8, Al10 and Al12. Cox et al. [27] experimentally found that the spin multiplicity of small Al clusters (n < 10) is 2 for clusters with odd number of atoms and 3 for clusters with even number of atoms. Interestingly, we observed that increasing the spin multiplicity of clusters to 4, 5, and 6 do not affect final structure of the clusters; however, clusters with higher spin multiplicity are very unstable energetically (in some cases more than 2 eV). Results of Table 1 show that the dipole moment of Al clusters strongly depend on the size and structural symmetry of the clusters which is in agreement with the results of references [2, 28, 29]. It has been reported that clusters with odd number of atoms are less symmetric and have larger values of dipole moment while clusters with even number of atoms are more symmetric and have smaller values of dipole moment [2]. Among Al n clusters; Al5, Al7, Al10, and Al13 have the highest values of dipole moment.

For the most stable Al n clusters we investigate some important properties as a function of cluster size. The relative stability of the Al n clusters has been investigated according to the binding energy per atom, second-order difference of cluster energies, and fragmentation energy.

The binding energy per atom of clusters was calculated according to the Eq. 1.

$$ E_b = \frac{{nE({\text{Al}}) - E({\text{Al}}_n )}}{n} $$
(1)

where in this equation n is the number of Al atoms in cluster, E(Al)is the energy of Al atom in the most stable state and E(Al n )is the energy of the most stable Al n cluster. Variation of binding energy per atom as a function of cluster size is shown in Fig. 2a. According to this figure the binding energy per atom increases monotonically to the maximum value of 2.01 eV for Al13 cluster while is smaller than the Al bulk cohesive energy of 3.39 eV [2]. Distinctive regions which separated from each other at n = 3, 7, and 10 are also observed in Fig. 2a.

Fig. 2
figure 2

Variation of binding energy per atom (a), second-order difference of cluster energies (b), fragmentation energy (c), and average Al–Al distance (d) for Al n clusters as a function of cluster size computed at B3LYP/6–31 + G* level of theory

Full size image

To gain better insight about the relative stability of clusters, it is more instructive to analyze the second-order difference of cluster energies (Δ 2 E) and fragmentation energy (E f) which were calculated according to the Eqs. 2 and 3, respectively [8].

$$ \varDelta_2 E({\text{Al}}_n ) = E({\text{Al}}_{n + 1} ) + E({\text{Al}}_{n - 1} ) - 2E({\text{Al}}_n ) $$
(2)
$$ E_f ({\text{Al}}_n ) = E({\text{Al}}) + E({\text{Al}}_{n - 1} ) - E({\text{Al}}_n ) $$
(3)

where E(Al n−1), and E(Al n+1) are the energies of the most stable Al n−1, and Al n+1 clusters, respectively.

Figure 2b presents variation of second-order difference of cluster energies (Δ 2 E) as a function of cluster size where maxima are found at n = 3, 7, and 10 indicating more stability of these clusters compared to their neighbor clusters.

The fragmentation energy show the relative stability of clusters compared to the neighboring clusters. The higher value of fragmentation energy indicates stronger Al–Al interaction and, therefore, higher energy is required for evaporation of Al atom from the cluster (more stability of the cluster). According to the results of fragmentation energy (E f ) which are shown as a function of cluster size in Fig. 2c, it is obvious that Al3, Al7, and Al10 clusters are more stable than their neighbor clusters. Overall, according to the binding energies per atom, second-order difference of cluster energies, and fragmentation energies it can be concluded that Al7 is the most stable cluster among all Al n clusters studied here.

Figure 2d shows variation of average Al–Al distance of the most stable clusters as a function of cluster size. As can be seen in this figure the average Al–Al distance gradually increases with cluster size while having local oscillation at Al5, Al8 and Al12 and finally approaches the bulk limit of 2.86 Å [2]. It seems that, unlike binding energy per atom, the average Al–Al distance of the most stable Al n clusters approaches the bulk value rather rapidly with cluster size.

The reactivity of molecules can be investigated using global (chemical) hardness (η) [30]. Chemical hardness is defined as the second derivative of energy with respect to the number of electrons at constant external potential. Using the finite difference approximation chemical hardness can be expressed as, η = (IP − EA)/2 [30], where IP and EA are the first ionization potential and electron affinity of the chemical system, respectively. Chemical hardness is resistance of a chemical entity to change in the number of electrons. Energetically speaking, hardness is one-half of the energy change for the disproportionation of a special chemical species according to the S + S → S + + S − reaction [30]. Since always IP S  ≥ EA S , the minimum value of hardness is zero. Zero hardness indicates maximum softness and maximum softness means no energy change associated with the disproportionation reaction (S + S → S + + S −). For example, a bulk metal has IP = EA (η = 0) and maximum softness [30].

The chemical hardness was calculated approximately according to the Eq. 4 [31, 32].

$$ \eta \cong \frac{E_{\text{LUMO}} - E_{\text{HOMO}} }{2} $$
(4)

where E LUMO and E HOMO are the energies of lowest unoccupied molecular orbital (LUMO) and highest occupied molecular orbital (HOMO) respectively.

Figure 3 presents variation of chemical hardness of Al n clusters as a function of cluster size. The general trend of Fig. 3 is oscillating behavior of the chemical hardness as a function of cluster size. Such an oscillating behavior is also reported for Zr n O2n H2 [33], Al–Au [34, 35], and Pd [1] clusters. According to this figure, Al6 and Al13 have the maximum hardness while Al2 and Al9 have the minimum hardness. Therefore, it can be concluded that Al6 and Al13 clusters have minimum tendency to exchange electrons (minimum reactivity) while Al2 and Al9 clusters have maximum tendency to exchange electrons (maximum reactivity).

Fig. 3
figure 3

Variation of chemical hardness for Al n clusters as a function of cluster size computed at B3LYP/6–31 + G* level of theory

Full size image

Al n Si m clusters (n = 4–6, m = 1–3, n + m = 5–7)

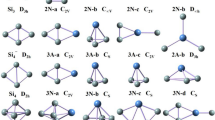
Several possible structures for Al n Si m clusters as input file at different spin multiplicities (1, 3, 5 for clusters with even electron numbers and 2, 4, 6 for clusters with odd electron numbers) were optimized at B3LYP level of theory using 6–31 + G* basis set. Figure 4a–c presents the most stable structure of Al n Si m clusters along with the corresponding spin multiplicities. Other higher energy structures along with the corresponding spin multiplicities as well as relative energies are collected as supporting information in table S.3. The calculated vibrational frequencies of most stable structures of Al n Si m clusters computed at B3LYP/6-31 + G* level of theory are collected as supporting information in table S.4. Like Al5 cluster, the Al4Si, Al3Si2, and Al2Si3 clusters have planer structures. Therefore, it seems that substitution of Al atom(s) with Si atom(s) in Al5 cluster do not change the geometry of theses clusters significantly. Unlike previous clusters, effect of Al atom(s) substitution with Si atom(s) on the geometry of Al6 is significant as clearly shown in Fig. 4b. While the geometry of Al6 and Al5Si is trigonal prism, the geometry of Al3Si3 is tetragonal bipyramid. The tetragonal bipyramid geometry has been reported as the most stable structure of pure Si6 cluster [10, 23]. Therefore, with increasing the amount of Si, the geometry of cluster changes from trigonal prism for pure Al6 cluster toward tetragonal bipyramid for pure Si6 cluster.

Fig. 4
figure 4

The most stable structure of Al n Si m clusters along with the corresponding spin multiplicities computed at B3LYP/6–31 + G* level of theory

Full size image

According to the Fig. 4c, substitution of Al atom(s) with Si atom(s) in Al7 cluster has also small effect on the geometry of clusters.

Effect of cluster composition on the stability of Al n Si m clusters was discussed using binding energy per atom and fragmentation energy. The binding energy per atom of Al n Si m clusters was calculated according to the Eq. 5.

$$ E_b = \frac{{nE({\text{Al}}) + mE({\text{Si}}) - E({\text{Al}}_n {\text{Si}}_m )}}{n + m} $$
(5)

where in this equation m is the number of Si atoms in cluster, E(Si)is the energy of Si atom in the most stable state and E(Al n Si m )is the energy of the most stable Al n Si m cluster.

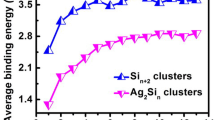
Variations of binding energy per atom of Al n Si m clusters as a function of atomic percentage of Si are shown in Fig. 5. The binding energies per atom increase linearly with adding Si to the pure Al n clusters indicating that the stability of clusters can improve with increasing the amount of Si.

Fig. 5
figure 5

Variation of binding energy per atom of Al n Si m clusters as a function of atomic percentage of Si computed at B3LYP/6–31 + G* level of theory

Full size image

The fragmentation energy of Al n Si m clusters was calculated according to the Eq. 6

$$ E_f ({\text{Al}}_n {\text{Si}}_m ) = E({\text{Al}}) + E({\text{Al}}_{n - 1} {\text{Si}}_m ) - E({\text{Al}}_n {\text{Si}}_m ) $$
(6)

Variations of fragmentation energy of Al n Si m clusters as a function of atomic percentage of Si are shown in Fig. 6 where the most important feature is the oscillating behavior of E f . The maxima appear in m = 3, 2, and 0 for clusters with n + m = 5, 6, and 7, respectively, indicating more stability of Al2Si3 (60 % Si), Al4Si2 (33.33 % Si), and Al7 clusters among clusters with similar number (n + m) of atoms. It can be concluded that Al–Si interaction in Al2Si3 and Al4Si2 clusters is stronger than Al–Al interaction in Al5 and Al6 clusters, respectively, and evaporation of Al atom from Al2Si3 and Al4Si2 clusters requires more energy compared to the corresponding Al5 and Al6 clusters, respectively. For Al7 cluster, on the other hand, Al–Al interaction is stronger than Al–Si interaction in Al6Si, Al5Si2, and Al4Si3 clusters and evaporation of Al atom from Al7 cluster requires more energy than Al6Si, Al5Si2, and Al4Si3 clusters.

Fig. 6
figure 6

Variation of fragmentation energy of Al n Si m clusters as a function of atomic percentage of Si computed at B3LYP/6–31 + G* level of theory

Full size image

The chemical hardness of Al n Si m clusters was calculated according to the Eq. 4 and results as a function of atomic percentage of Si are shown in Fig. 7. The most important feature of Fig. 7 is oscillating behavior of chemical hardness as a function of atomic percentage of Si. Therefore, some of Al n Si m clusters are softer than corresponding pure Al n clusters while some others are harder. The Al2Si3 and Al4Si2 clusters have the maximum values of chemical hardness among all clusters studied here.

Fig. 7
figure 7

Variation of chemical hardness of Al n Si m clusters as a function of atomic percentage of Si computed at B3LYP/6–31 + G* level of theory

Full size image

Effect of basis set was investigated on the electronic properties of clusters considering 6–31 + G*, 6–31 + G** and 6–311 + G* basis sets. The calculated results are shown in Tables 2 and 3 for Al n and Al n Si m clusters, respectively. It is clear that basis set has no significant effect on the binding energy per atom, second-order difference of cluster energies and chemical hardness of clusters. Effect of basis set on the fragmentation energy of clusters is very little, but similar trend is observed for different basis set nevertheless.

Table 2 The calculated electronic properties of Al n clusters at different basis sets
Full size table
Table 3 The calculated electronic properties of Al n Si m clusters at different basis sets
Full size table

Conclusions

The geometry, stability and properties of Al n (n = 1–13) and Al n Si m (n + m = 5–7) nanoclusters at B3LYP level of theory using 6–31 + G* basis set were investigated. The binding energy per atom of pure Al n clusters increases monotonically to the maximum value of 2.01 eV for Al13 cluster while is smaller than the Al bulk cohesive energy of 3.39 eV. Analysis of binding energy per atom, second-order difference of cluster energies, and fragmentation energy reveals that Al3, Al7, and Al10 clusters are more stable than their neighbor clusters. It is observed that Al7, Al2Si3 (60 % Si) and Al4Si2 (33.33 % Si) clusters have the maximum stability among pure and mixed clusters, respectively. Substituting of Al atom(s) with Si atom(s) change geometry of some clusters significantly while the geometry of some others remains without significant variation. Our results show that Al–Si interaction in Al2Si3 and Al4Si2 clusters is stronger than Al–Al interaction in Al5 and Al6 clusters, respectively, which means that evaporation of Al atom from Al2Si3 and Al4Si2 clusters requires more energy compared to the corresponding Al5 and Al6 clusters, respectively. For Al7 cluster, on the other hand, Al–Al interaction is stronger than Al–Si interaction in Al6Si, Al5Si2, and Al4Si3 clusters indicating that evaporation of Al atom from Al7 cluster requires more energy than Al6Si, Al5Si2, and Al4Si3 clusters. It is found that the chemical hardness of Aln and Al n Si m clusters strongly depends on the cluster size as well as cluster composition.