Introduction

Carbon forms a variety of nanostructures in which C60 fullerene is particularly remarkable due to its finite size and for many technological applications [1, 2]. The electronic properties of fullerenes have been found to be affected by doping of atoms [3] and molecule [4]. Introduction of heteroatoms into C60 fullerene leads to distinguished physical and chemical properties which make them promising materials for some unique applications [5–7]. In particular, BN substituted C60 cages have been studied several times [8–14]. Esfarjani et al. [8] have studied the band structure and chemical bonding in BNC58 heterofullerenes and its electronic spectra are studied by Chen et al. [9]. Krainara et al. [10] and Siddiqui et al. [11] have studied the interaction of BNC58 with adenine Cu(II) complexes and suggested that this heterofullerene is capable to differentiate electronically equivalent tautomers of DNA base pair. A systematic study on C60−2x (BN) x (x = 1–7) hybrid fullerene has been performed by Pattanayak et al. [12] and subsequently extended up to C12B24N24 [13]. Anafcheh et al. [14] have recently performed NMR calculations on C60−2x (BN) x (x = 1, 2, 3, 6, 9, 12, 15, 18, 21, and 24) using density functional theory (DFT). The uniqueness of BN doped C60 is due to the fact that polar BN bond is analogous to covalent CC bond in many aspects [15]. For instance, borazine (B3N3H6) shows a great similarity with that of benzene (C6H6) [16–18] and hence, it is regarded as inorganic benzene. However, it is noticeable that the polarity of the BN bond causes borazine to show a reactivity pattern different from that of benzene. For instance, benzene is aromatic, but borazine is probably non-aromatic. Furthermore, BN analogs of many carbon nanostructures such as boron-nitride nanotubes, boron-nitride nanosheets, etc., have been well studied and reported. One might, therefore, expect that BN substituted C60 fullerenes are structurally analogous to pure C60. Therefore, it should be interesting to analyze the effect of this substitution on the physical and chemical properties of C60. In this paper, we report density functional theory-based study on a substituted C60 in which one of C6 hexagons is replaced by B3N3. Spectral properties such as infrared, Raman and NMR spectra provide the signature of the molecular structure. Therefore, we analyze the spectral features of B3N3C54 and compare it with C60. Moreover, the electronic properties of B3N3C54 heterofullerene have been explored and compared with those of C60.

Computational methods

The study was performed using density functional theory (DFT) method as implemented in Gaussian 09 program [19]. All structures considered in this were fully optimized without any symmetry constraint using B3LYP exchange–correlation functional [20, 21] with 6-31G(d) basis set. The B3LYP scheme has already been used in our previous study on LiF nanostructures [22]. More recently, B3LYP/6-31G(d) level has been proved to yield accurate results in case various fullerene derivatives [23]. Vibrational frequency calculations and natural population analysis (NPA) have been carried out within the same computational scheme. In a recent study, we have noticed that NPA charges are more reliable than many other population schemes [24].

Results and discussion

Structure and energetics

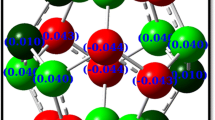
The optimized structure of B3N3C54 along with C60 is displayed in Fig. 1. One can note that the structure of B3N3C54 closely resembles that of C60 in which one of C6 hexagons is replaced by B3N3, but its symmetry is reduced to C 3 point group. To get further insights, we have separately optimized C6 and B3N3. After optimization, we have found that they are almost similar in structure, also shown in Fig. 1. Both possess D 3h symmetry and equalized bond lengths, 1.358 Å for B–N and 1.327 Å for C–C. The NPA charges on B and N atoms in B3N3 are +1.04e and −1.04e, respectively, which suggest polarity of BN bonds. In Table 1, we have collected the bond lengths of hexagon–hexagon and hexagon–pentagon in B3N3C54 and C60. Evidently, the B–N bond lengths increase to 1.437 Å and 1.478 Å in hexagon–hexagon and hexagon–pentagon edges which indicate that B–N bonds of the substituted fullerene are weaker than those of free B3N3. Furthermore, the difference of B–N and C–C bond lengths is significantly increased. This may be expected due to redistribution of charges on B and N atoms in B3N3C54. For instance, NPA charges on B and N atoms in B3N3C54 are +1.02e and −0.88e, respectively. One can note that the polarity of BN bonds reduces in B3N3C54 which weakens the bond increasing its bond length.

Fig. 1
figure 1

Equilibrium structures of C60 (left) and B3N3C54 (right) calculated at B3LYP level

Full size image
Table 1 Main bond lengths (in Å) of B3N3C54 and C60 at B3LYP/6-31G(d) level
Full size table

The formation of B3N3C54 involves two processes: the removal of C6 hexagon from C60 and then, inclusion of B3N3 hexagon at the same place. The corresponding stabilization energy can be calculated by,

$$\Delta E = E\left[ {{\text{B}}_{3} {\text{N}}_{3} {\text{C}}_{54} } \right] \, + E\left[ {{\text{C}}_{6} } \right] - E\left[ {{\text{C}}_{60} } \right] - E\left[ {{\text{B}}_{3} {\text{N}}_{3} } \right]$$

where E[..] represents the total electronic energy of respective species including zero point correction. The calculated E values are −2296.5835, −2286.1742, −238.8580, and −228.2520 a.u. for B3N3C54, C60, B3N3, and C6, respectively, at B3LYP/6-31G(d) level. Therefore, ΔE value is found to be 5.35 eV which is positive and large enough to establish that the B3N3C54 heterofullerene is kinetically stable.

Spectral properties

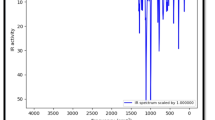
We have calculated vibrational infrared, Raman and NMR spectra of B3N3C54 and compared with those of C60. The vibrational frequency calculations performed on B3N3C54 heterofullerene reveal all real and positive values. This suggests that B3N3C54 belongs to at least some local minimum in the potential energy surface. The calculated vibrational infrared and Raman spectra of B3N3C54 and C60 are depicted in Fig. 2. For N-polyatomic systems, there are 3N-6 normal modes of vibration. Due to extremely high symmetry of C60 (I h point group), however, there are only four characteristic modes possessing appreciable intensity. The mode with the highest intensity is assigned at the lowest wavenumber, 537 cm−1. The CC stretching modes of C60 are assigned in the higher wavenumber region, 1460 and 1214 cm−1. The calculated wavenumbers were scaled by a factor of 0.9613 as suggested by Merrick et al. [25]. The scale wavenumbers of C60 516, 565, 1167 and 1404 cm−1 are in accordance with the FT-IR frequencies 526, 576, 1183 and 1429 cm−1, respectively, as reported by Chase et al. [26]. The substitution of B3N3 into C60 leads to destruction of the sharpness of peaks in the IR spectrum due to C 3 point group. As seen in Fig. 2, a number of additional modes and mixing of various modes appear due to BN, BC and NC stretchings. For instance, the BN stretching modes appear at 1394 cm−1. This mode possesses the strongest intensity due to charge transfer from B to N atoms. Furthermore, CC stretching modes of B3N3C54 are shifted toward higher wavenumber region as compared to C60. For example, the modes calculated at 1606 and 1586 cm−1 are assigned to CC stretchings with weak intensities. However, CC stretching and lower wavenumber mode of B3N3C54 corresponding to C60 are obtained at 1468 cm−1 (medium) and 539 cm−1 (weak). On the contrary, Raman spectrum of B3N3C54 closely resembles that of C60. There are eight distinct modes of vibrations in the Raman spectra which are in accordance with the experimental reports of Bethune et al. [27, 28]. For instance, the most intense Raman peak calculated at 1465 cm−1 is observed at 1469 cm−1 in C60 solid film [27] and 1470 cm−1 in C60 thin film [28].

Fig. 2
figure 2

Vibrational infrared and Raman spectra of B3N3C54 and C60 calculated at B3LYP/6-31G(d) level

Full size image

NMR spectra of B3N3C54 and C60 are calculated by gauge independent atomic orbital (GIAO) approach at B3LYP/6-31G(d) level. The NMR relative chemical shifts of nucleus ‘X’ are calculated by δ = δref − δfull, where δfull are isotropic magnetic shieldings of nuclei of fullerene and δref are those of reference systems which are C4H12Si for C, B2H6 for B and NH3 for N nucleus. The calculated chemical shift for C60 is 131.8 ppm whereas that of B3N3C54 lies between 121.5 and 143.9 ppm. The minimal δ value corresponds to C attached to C–B bond whereas maximal value belongs to C bonded to C–N moiety, as expected due to lone pair of N atom. The triply degenerate NMR peaks of B and N nuclei in B3N3C54 are found to be at 10.1 and 162.8 ppm, respectively.

Electronic properties

The density of states (DOS) spectra along with molecular orbital energy levels of B3N3C54 and C60 are plotted in Fig. 3. One can note that the energy levels of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of B3N3C54 are slightly shifted upwards relative to C60. Furthermore, the substitution results in additional energy levels which are closely spaced and broaden the density of states spectrum. The DOS spectra also reveal that the HOMOs of C60 are fivefold degenerate and LUMOs are triply degenerate. This degeneracy of molecular orbitals is lowered for B3N3C54 in which the HOMOs and LUMOs are triply and doubly degenerate, respectively. The degenerate HOMOs and LUMOs of B3N3C54 and C60 are displayed in Fig. 4. Within the framework of Koopmans’ theorem, the ionization potential (I) and electron affinity (A) are approximated by the negative energy eigenvalues of the HOMO and LUMO, respectively. From Table 2, one can note that the calculated I and A values of B3N3C54 are lower than those of C60. As known, it is energetically unfavorable to add electrons to a high-lying LUMO or to extract electrons from a low-lying HOMO and so to form the activated complexes of any potential reaction [29]. Therefore, B3N3C54 is expected to be form cationic complexes due to smaller E HOMO magnitude, i.e., I value than that of C60.

Fig. 3
figure 3

Density of States (DOS) spectra of C60 and B3N3C54 calculated at B3LYP level. Occupied (green) and unoccupied (blue) molecular orbital energy levels are also displayed

Full size image
Fig. 4
figure 4

Degenerate HOMOs and LUMOs of B3N3C54 (upper set) and C60 (lower set)

Full size image
Table 2 Electronic parameters of B3N3C54 and C60 at B3LYP/6-31G(d) level
Full size table

The energy difference between HOMO and LUMO, HOMO–LUMO energy gap (E gap) corresponds to the band gap in solids which is equal to the difference of I and A values. In molecular system, this energy gap is generally approximated to the chemical hardness [30]. This energy gap is equivalent to the energy required to free an outer shell electron which behaves as a mobile charge carrier that moves freely within the solid material. The E gap is an important parameter that determines the electrical conductivity of a solid. Substances with larger energy gaps are generally insulators, materials with smaller energy gaps are semiconductors, and conducting materials have very small or no energy gaps. In other words, the molecules with smaller energy gaps are less hard, and hence more reactive. Our calculated E gap of C60 at B3LYP/6-31G(d) level (2.76 eV) is in agreement with the experimental band gap value of 2.3 ± 0.1 eV [31]. This energy gap being neither too large nor too small suggests the semiconducting behavior of C60. In case of B3N3C54, this energy gap is reduced to 2.67 eV. Therefore, the conductivity of B3N3C54 should be slightly greater than that of C60.

Conclusion

Using density functional theory-based calculations; we have studied the substitution of B3N3 hexagon into C60 fullerene. We noticed that the structure of B3N3C54 closely resembles that of C60. However, polar B–N bonds are weaker than that of covalent C–C bonds. The stabilization energy due to substitution of B3N3 into C60 is calculated to be 5.35 eV at B3LYP/6-31G(d) level. The vibrational infrared and Raman spectra of B3N3C54 and C60 have been compared and it was noticed that the strongest peak in vibrational spectrum of B3N3C54 is due to BN stretching and CC stretching modes are shifted to higher wavenumber region. The NMR chemical shifts of B3N3C54 have also been computed. The density of states (DOS) spectrum of B3N3C54 shows the reduction in the degeneracy of molecular orbitals, but enhancement in the peak width resulting in additional energy levels due to heteroatoms such that its HOMO–LUMO gap is reduced relative to C60. This study should provide better insights into the surface modification of C60 by heteroatom.