Introduction

The solar energy constitutes the biggest source of energy in our world. This kind of energy is clean, cheap, endless, and reachable in most parts of the planet. Nowadays, according to the limitations of fossil fuels and their proved consequences on climate change and global warming, there is an increasing attention to solar energy all around the world.

Solar cells are often used to get energy from the sun light, especially when the electrical energy is needed. It yields the fact that analysis and predicting the behavior of solar cells at different working conditions with a high precision is of high importance in practice. Of course, this task cannot be performed without accurate modeling of these devices. So far, various electrical models have been developed for extracting the I–V curve of solar cells (see, for example, [1–4] and the references therein). Among others, the so-called single- and double-diode models are more often used in practice. At this time, a variety of methods are available for parameter estimation of these two electrical models. Some attempts in this field are focused on using classical analytical and numerical methods for parameter estimation based on minimization of a suitably chosen cost function [1, 5–10]. The main drawback of such classical methods is the high probability of falling in local optimums, besides the complexity of calculations.

In recent years, according to the advances in the field of meta-heuristic optimization algorithms, these methods are also widely used for parameter estimation of solar cell models. For example, application of genetic algorithm (GA) [11–13], particle swarm optimization (PSO) [14–16], simulated annealing (SA) [17], differential evolution (DE) [18–22], pattern search (PS) [23], harmony search (HS) [24], artificial bee swarm optimization (ABSO) [25], bird mating optimizer (BMO) [26], bacterial foraging optimization (BFO) [27], artificial bee colony (ABC) [28], biogeography-based optimization algorithm with mutation strategies (BBO-M) [29] and teaching–learning based optimization (TLBO) [30] for this purpose can be found in the literature.

As a well-known fact, any optimization algorithm has its own advantages and disadvantages. For example, GA is often known for its slow convergence. PSO is fast but commonly the accuracy of solutions is not increased by increasing the number of iterations (to be adjusted by trial and error) [31]. High sensitivity to the initial guess and low probability of finding the global optimum are the main drawbacks of SA. A similar discussion goes on other optimization algorithms. In general, algorithms with smaller number of parameters (to be adjusted by user by trial and error), faster convergence and higher probability of skipping from local optimums are identified as more effective algorithms. It is very important to note that effectiveness of a certain algorithm strictly depends on the problem it is going to solve. In other words, it may happen that a certain algorithm be very successful in dealing with a problem while it is quite unsuccessful in dealing with another one. For this reason and as a common practice, researchers apply different techniques to a certain problem to find the best method suited to solve it. More often authors try to combine two or more methods in a single hybrid one [32–34]. The aim is to use different models with unique features to overcome the single negative performance and finally improve the performances. Hence, proposing the most effective algorithm (i.e., the one at once with the highest accuracy, fastest convergence, smallest number of parameters, most ease of use, etc.) for parameter estimation of solar cell models is of high importance in practice.

The main aim of this paper is to develop a modified explanation of artificial bee colony (ABC) algorithm, MABC, and study its applications for parameter estimation of single- and double-diode solar cell models and compare the results with competing methods. ABC, which is inspired from the behavior of honey bees in nature, is originally developed by [35] as a tool for solving nonlinear optimization problems. So far, this algorithm has been successfully used for solving wide variety of real-world problems (see, for example [36–38], for some very recent applications of this algorithm). In this paper, we have modified the definition of the so-called scout bees in classical ABC algorithm to arrive at a version of this algorithm which, compared to all previous studies, is highly effective for solving the problem under consideration (and probably many others as well).

The rest of this paper is organized as the following. Formulation of the problem is presented in “Problem description” section. In this section, single- and double-diode models are reviewed and the proposed objective function is introduced. The ABC algorithm is briefly reviewed in “Summary of ABC Algorithm” section and the proposed modification is also presented in this section. In “Proposed ABC algorithm” section, the proposed ABC algorithm is applied to some benchmark functions and the results are compared with those obtained using other modified ABC algorithms. “Simulation results for benchmark function” section is devoted to simulation results. In this section, the proposed approach is used for parameter estimation of single- and double-diode models and the results are compared (from different aspects) with other algorithms. Finally, “Results and discussion” section concludes the paper.

Problem description

As mentioned before, it is common practice to model solar cells using the so-called single- and double-diode models, where the parameters of these models are often calculated by minimization of a suitably chosen cost function. In the following, first we briefly review these two electrical models and then we introduce our proposed cost function to be minimized.

Double-diode model of solar cells

The double-diode electrical model of solar cells is shown in Fig. 1. According to this figure, the electrical current passing through the load is obtained as the following [4]:

$$ I_{\text{L}} = I_{\text{ph}} - I_{{\text{d}}1} - I_{{\text{d}}2} - I_{\text{sh}} $$
(1)

where I ph is the electrical current generated by solar cell, I d1 is the electrical current of first diode, I d2 is the electrical current of second diode, I sh is electrical current of shunt resistor and I L is the electrical current passing through the load connected to solar cell. I d1 and I d2 in (1) are calculated through the Shockley equation as the following:

$$ I_{{\text{d}}1} = I_{{\text{sd}}1} [{\exp ({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{n_1 kT}}) - 1}] $$
(2)
$$ I_{{\text{d}}2} = I_{{\text{sd}}1} [{\exp ({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{n_2 kT}}) - 1}] $$
(3)

where R s is the resistor in series with load, I sd1 and I sd2 are the reverse bias saturation currents, V L is the load voltage, n 1 and n 2 are the diode ideality factors, k is the Boltzmann constant, q is the electric charge of electron and T is the absolute temperature of solar cell in Kelvin. On the other hand, according to Fig. 1, I sh is calculated as the following:

$$ I_{\text{sh}} = \frac{{V_{\text{L}} + R_{\text{s}} I_{\text{L}} }}{{R_{\text{sh}} }} $$
(4)
Fig. 1
figure 1

The double-diode model of solar cells

Full size image

Substitution of I d1, I d2 and I sh from (2), (3), and (4) in (1) yields:

$$ I_{\text{L}} = I_{\text{ph}} - I_{{\text{sd}}1} \left[{\exp \left({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{n_1 kT}}\right) - 1}\right] - I_{{\text{sd}}2} \left[{\exp \left({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{n_2 kT}}\right) - 1}\right] - \frac{{V_{\text{L}} + R_{\text{s}} I_{\text{L}} }}{{R_{\text{sh}} }} $$
(5)

Hence, the output power of the solar cell under consideration is obtained as:

$$ P_{\text{L}} = \left\{{I_{{\text{ph}} - I_{{\text{sd}}1} } \left[{\exp \left({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{n_1 kT}}\right) - 1}\right] - I_{{\text{sd}}2} \left[{\exp \left({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{n_2 kT}}\right) - 1}\right] - \frac{{V_{\text{L}} + R_{\text{s}} I_{\text{L}} }}{{R_{\text{sh}} }}}\right\}V_{\text{L}} $$
(6)

In the double-diode model, as discussed above, the seven parameters {n 2, n 1, R sh, R s, I sd2, I sd1, I ph} are considered as unknown parameters of problem to be estimated.

Single-diode model of solar cells

The single-diode model as shown in Fig. 2 is the most widely used model for extracting the I–V curve of solar cells. According to this figure, the load current provided by cell is obtained as the following:

Fig. 2
figure 2

The single-diode model of solar cells

Full size image
$$ I_{\text{L}} = I_{\text{ph}} - I_{{\text{sd}}1} \left[{\exp \left({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{nkT}}\right) - 1}\right] - \frac{{V_{\text{L}} + R_{\text{s}} I_{\text{L}} }}{{R_{\text{sh}} }} $$
(7)

This leads to the following formula for the power generated by this cell.

$$ P_{\text{L}} = \left\{{I_{\text{ph}} - I_{{\text{sd}}1} \left[{\exp \left({\frac{{q({V_{\text{L}} + R_{\text{s}} I_{\text{L}} })}}{nkT}}\right) - 1}\right] - \frac{{V_{\text{L}} + R_{\text{s}} I_{\text{L}} }}{{R_{\text{sh}} }}}\right\}V_{\text{L}} $$
(8)

In the single-diode model shown in Fig. 2 {I ph, I sd1, R s, R sh, n} are assumed to be the unknown parameters to be estimated.

Objective function

As mentioned before, the single- and double-diode models consist of five and seven unknown parameters, respectively, which are determined by solving a root mean square error (RMSE) optimization problem in this paper. For this purpose, the load current is calculated and measured at different working conditions and the unknown parameters are calculated such that the proposed objective function defined as the following:

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum_{i = 1}^N {({I_{{\text{L}},i} - I_{{\text{meas}},i} })^2 } } $$
(9)

where N is the number of measurements, and I L,i and I meas,i stand for the ith calculated and measured load currents, respectively.

In this paper, a modified explanation of ABC algorithm is proposed to find the value of unknown parameters of model; the cost function given in (9) is minimized.

Summary of ABC algorithm

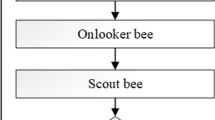
The ABC algorithm, which belongs to the family of nature-inspired meta-heuristic optimization algorithms, was first introduced in 2005 by Karaboga [35]. This algorithm is inspired from the behavior of honey bees in nature and provides us with a powerful tool for solving complex optimization problems. In the ABC algorithm, artificial bees in the colony are divided into three parts: employed bees, onlooker bees, and scout bees. Employed bees (whose number is equal to onlooker bees) discover the food sources, bring the food to hive and share its location with other bees. Onlooker bees stay in the hive and decide to follow the employed bees based on the quality of the food sources they have discovered. Scout bees randomly search the outdoor (independent of employed bees) to find (probably better) unseen food sources. In ABC algorithm, the location of each food source identifies a point in the domain of problem (i.e., a potential solution) and points with smaller value for cost function are assumed to be better food sources (better solutions).

Mathematically, in the first step of algorithm, the solution vectors are selected randomly from the domain of problem. For this purpose, position of the nth artificial bee (n = 1, 2, …, SN) is considered as the following:

$$ X_n = [{x_{n1} ,x_{n2} , \ldots ,x_{nm} }] $$
(10)

where SN and m stand for the number of artificial bees and number of variables, respectively, and x n1, x n2, …, x nm are random numbers selected from the domain of definition of problem. At each step, employed bees search around the food sources x n (i.e., the previous solutions in their memory) to find the potentially better sources v n  = [v n1, v n2, …, v nm ], where the components of x n and v n are related through the following equation:

$$ v_{ni} = x_{ni} + \phi ({x_{ni} - x_{ki} }) $$
(11)

In the above equation, k (\( k \ne n \)) is a randomly selected integer in the range [1,SN] and \( \phi_{ni} \) is a random number with uniform distribution selected from [−1,1]. The new solution v n is replaced with the previous one, x n , if f(v n ) < f(x n ), where f is the m-variable cost function to be minimized. Else, the previous one is retained.

After calculating the location of new sources from (11) and performing necessary substitutions, the fitness of each new source is calculated from the following equation:

$$ {\text{fit}}(X_n ) = \left\{ {\begin{array}{*{20}c} {\frac{1}{1 + f(X_n )}} & {\quad f(X_n ) \ge 0} \\ {1 + f(X_n )} & {\quad f(X_n ) < 0} \\ \end{array} } \right. $$
(12)

Where fit(x n ) is the fitness of the source located at x n , and fit(x n ) is the value of the (m-variable) cost function to be minimized at this point. Then, onlooker bees in the hive choose the employed bees of the next iteration based on the quality of their food sources. More precisely, first the probability of choosing the food source located at x n (to be used in the next iteration for further search around) denoted as P n is calculated as the following:

$$ P_n = \frac{{{\text{fit}}(X_n )}}{{\sum_{k = 1}^{\text{SN}} {{\text{fit}}(X_n )} }} $$
(13)

Then, a roulette wheel is used for determining the food sources to be used by employed bees in the next iteration (angles of the corresponding sectors of roulette wheel are considered proportional to the probabilities calculated from (13)). Note that at each iteration onlooker bees select exactly SN bees by chance and, consequently, some of the employed bees may not be selected at all, while some others are selected more than once. In the standard ABC algorithm, one of the employed bees is selected and classified as the scout bee [39] (later, this definition is slightly modified in [40]). The classification is controlled by a control parameter called “limit”. In this manner if a solution representing a food source is not improved after a predetermined number of successive trials, then that food source is abandoned by its employed bee and the employed bee associated with that food source becomes a scout, which searches around randomly. The number of trials for releasing a food source is equal to the value of “limit”, which is an important control parameter in ABC algorithm. In this paper, however, for increasing the accuracy of results we have adopted more than one scout bee (similar to [40]) and, moreover, the scout bees are assumed to follow the best employed bee of colony instead of performing a random search. More precisely, any employed bee that cannot find a better solution (compared to its previous findings) after ten successive iterations is considered as a scout bee who begins to follow the best bee of colony.

To sum up, at each iteration first the new locations are calculated from (11) and their qualities are evaluated through (12). Then, necessary substitutions are performed and the selection probabilities are calculated from (13). Next, some of these locations are selected by onlooker bees and the possible scout bee is determined, and this procedure is repeated until a certain termination condition is fulfilled. It is obvious that using this procedure low-quality food sources are most likely to be abandoned by onlooker bees and, as a result, employed bees tend to search around the locations with higher fitness values. The location with the highest fitness value (taking into account all iterations and all bees) is considered as the final solution (of course, for this purpose the best solution should be memorized at each iteration).

Proposed ABC algorithm

In the classical ABC algorithm, random selection of the location of scout bees reduces the effectiveness of algorithm. The reason (especially when the objective function is continuous and a large number of iterations is performed) is that it is very improbable that the point randomly selected by a scout bee be better than the solution obtained by cooperative search of employed bees after several iterations. However, in the proposed method the position of scout bee is considered equal to the position of the close to the best solution obtained so far, that is

$$ X_{\text{scout}} = X_{\text{best}} \times (1 + {\text{rand}}) $$
(14)

Obviously, using the above definition for scout bees leads to a more search around the best solution obtained so far. Currently, many methods are available to modify Eq. (11) [41–44]. Especially, in [40] \( \phi_{ni} \) is selected in the range [−SF,SF] (SF is the scaling factor) where SF is selected using Rechenberg’s 1.5 rule mutation during search. But in this paper, SF is modified through (15) which is inspired by the PSO algorithm:

$$ {\text{SF}} = \omega_{\hbox{max} } - \left({\frac{{\omega_{\hbox{max} } - \omega_{\hbox{min} } }}{\text{iter}}}\right){\text{iter}}_{\hbox{max} } $$
(15)

In the above equation, \( \omega_{\hbox{max} } \) and \( \omega_{\hbox{min} } \) are selected equal to 1 and 0.7, respectively. According to the above discussion and Table 1, the modified ABC algorithm to estimate the parameters of single- and double-diode models of solar cells is proposed as Fig. 3.

Fig. 3
figure 3

The flowchart of proposed algorithm

Full size image

Simulation results for benchmark function

To demonstrate the capabilities of the proposed algorithm, it is applied to some benchmark functions [45]. The mean result of 10 runs is summarized in Table 2. In this simulation, the population of bee colony is considered equal to 80 and the maximum number of iterations is equal to 5000. Several candidate values are considered for the limit values. The mean result of 10 runs for each limit is reported. As it can be observed in Table 2, the best candidate value is 0.06 itermax to 0.08 itermax. The result of proposed method is compared with the Gbest Algorithm in Table 3. Table 3 clearly shows that the proposed algorithm works better than the Gbest Algorithm.

Table 1 Lower and upper bounds of the parameters used in the solar cell model (both single- and double-diode models)
Full size table
Table 2 Results obtained for different values of limits value
Full size table
Table 3 Comparison between the proposed method and ABC [44], GABC [44] and GABC [28]
Full size table

Results and discussion

Experimental data used in simulations of this paper are adopted from [46] which correspond to a 57 mm diameter commercial (R.T.C France) silicon solar cell at 33 °C. Note that since meta-heuristic optimization algorithms are probabilistic in nature, in all the following simulations the algorithms under consideration are executed several times and the best result is presented at each case.

Parameter estimation of single-diode model

According to Fig. 4 for the single-diode model, the appropriate size of the bee colony is 100 and the number of maximum iteration is 600. Figure 5 demonstrates the distribution of objective function (RMSE) for single-diode model for 50 runs. As it can be observed, the average line is close to minimum line which shows the capability of proposed algorithm. The unknown parameters of the proposed method are obtained by minimization of the cost function given in (9). Note that since the exact value of parameters is not known, the only way for comparing the performance of different algorithms is to evaluate this index. In fact, the algorithm that leads to a smaller value for RMSE index is considered as a more effective one. Table 4 shows the values obtained for unknown parameters of model when nine different optimization algorithms (including the proposed MABC algorithm) are applied [24]. The corresponding RMSE indices are also presented in this table for comparing purposes. As it can be observed, GGHS, MABC and IADE lead to relatively closer values for RMSE index compared to others. To make a better comparison between these three algorithms, the absolute errors between measured and calculated currents and powers are calculated at each operating point through (16) and (17) and the results are plotted in Figs. 6 and 7.

Fig. 4
figure 4

Objective function under consideration versus a population number and b iteration number for single-diode model

Full size image
Fig. 5
figure 5

Distribution of the objective function (RMSE) for single diode model for 50 runs

Full size image
Table 4 Estimated values for unknown parameters of single-diode model (using nine different algorithms) and the corresponding RMSE indices
Full size table
Fig. 6
figure 6

Absolute error between measured and calculated currents in the single-diode model using three different algorithms

Full size image
Fig. 7
figure 7

Absolute error between measured and calculated powers in the single-diode model using three different algorithms

Full size image
$$ \varepsilon_{\text{current}} = | {I_{\text{L}} - I_{\text{measured}} } | $$
(16)
$$ \varepsilon_{\text{power}} = | {P_{\text{L}} - P_{\text{measured}} } | $$
(17)

As it can be observed in Fig. 6, at voltages between −0.2 and 0.45 V the MABC, IADE, and GGHS lead to almost the same values for absolute current error, while at voltages between 0.45 and 0.6 V the error caused by MABC is considerably smaller than IADE and GGHS. Similarly, Fig. 7 shows the absolute error in power versus voltage when again these three algorithms are applied. As it can be observed in this figure, MABC exhibits a considerably better performance, especially at voltages between 0.5 and 0.6 V.

Figures 8 and 9 show the P–V and I–V curves of the single-diode model (identified using the proposed MABC) and the corresponding experimental data points, respectively. As it is observed, the curves obtained using MABC perfectly match the real-world data points. This observation confirms the accuracy of the proposed method.

Fig. 8
figure 8

P–V curve of the single-diode model (obtained using the proposed MABC algorithm) and the experimental data points of solar cell

Full size image
Fig. 9
figure 9

I–V curve of the single-diode model (obtained using the proposed MABC algorithm) and the experimental data points of solar cell

Full size image

Another advantage of the proposed MABC algorithm is its very fast convergence. More precisely, in the above simulations, it was observed that MABC converges after about 600 iterations while ABSO (which is the fastest one among all the algorithms presented in Table 4, except MABC) converges after about 5000 iterations. Figure 10 shows the value of objective function versus iteration number when the proposed MABC [39] is applied. This figure clearly shows the considerably faster convergence of MABC, which also leads to a lower value for objective function. Note that finding smaller values for objective is equivalent to more accurate estimation of unknown parameters of the model.

Fig. 10
figure 10

Value of the objective function under consideration versus iteration number (single diode model)

Full size image

Table 5 represents the measured and calculated currents at 26 different working conditions and powers of the solar cell under consideration at 26 different working conditions when the proposed MABC algorithm is applied. Investigating the numbers presented in this table confirms the high accuracy of the proposed method for parameter estimation of single-diode models.

Table 5 Measured and calculated (using single-diode model and the proposed MABC algorithm) currents and powers of the solar cell at 26 different working conditions
Full size table

Parameter estimation of double-diode model

Table 6 shows the values obtained for unknown parameters of the double-diode model under consideration using seven different algorithms. According to Fig. 11 for a double-diode model, the appropriate size of the bee colony is 200 and maximum number of iterations is 600 where again the limitations of Table 1 are considered. Figure 12 demonstrates distribution of the objective function (RMSE) for double-diode model for 50 runs. In this figure, the average line is close to the minimum line which shows the capability of proposed algorithm. The corresponding RMSE indices are also presented in this table. Note that here the number of iterations of MABC algorithm is considered equal to 600 which is considerably smaller than the 5000 iterations used by ABSO and IGHS. Since in Table 6 ABSO, IGHS, and MABC lead to more closer values for RMSE performance index we have plotted the absolute current and power errors (calculated from (16) and (17), respectively) in Figs. 13 and 14 to make a better comparison. As it can be observed in these figures, the proposed MABC algorithm leads to considerably more accurate results both in current and power estimations, especially in the voltage range 0.45 to 0.6 V.

Table 6 Estimated values for unknown parameters of double-diode model (using seven different algorithms) and the corresponding RMSE indices
Full size table
Fig. 11
figure 11

Objective function under consideration versus Population number and Iteration number for double-diode model

Full size image
Fig. 12
figure 12

Distribution of the objective function (RMSE) for double-diode model for 50 runs

Full size image
Fig. 13
figure 13

Absolute error between measured and calculated currents of the double-diode model using three different algorithms

Full size image
Fig. 14
figure 14

Absolute error between measured and calculated powers of the double-diode model using three different algorithms

Full size image

To study the accuracy of the double-diode model obtained using MABC algorithm, the corresponding P–V and I–V curves of the model and real-world solar cell are shown in Figs. 15 and 16, respectively. As it can be observed, at each figure the curve of model perfectly matches the corresponding data points of the real-world solar cell. This observation again verifies the accuracy of the proposed method.

Fig. 15
figure 15

P–V curve of the double-diode model (obtained using the proposed MABC algorithm) and the experimental data points of solar cell

Full size image
Fig. 16
figure 16

I–V curve of the double-diode model (obtained using the proposed MABC algorithm) and the experimental data points of solar cell

Full size image

The last simulation of this paper studies the effect of the proposed modification in ABC algorithm on its performance. For this purpose, the value of objective function (RMSE) is plotted versus the iteration number in Fig. 17 As it can be observed, this figure clearly shows the considerably faster convergence. Note that, as it is expected, the values obtained for objective function in double-diode case are typically smaller than the values obtained for it in single-diode case (compare Figs. 10, 17). However, since in Fig. 17 MABC leads to slightly smaller values for objective function, it is expected that the corresponding double-diode model also be more accurate.

Fig. 17
figure 17

Value of the objective function under consideration versus iteration number (double-diode model)

Full size image

Finally, relative errors between estimated (using double-diode model) and measured currents and powers are summarized in Table 7 for 26 different working conditions when MABC is applied. According to the data presented in this table, it can be easily verified that MABC has estimated both the current and power with a very high accuracy.

Table 7 Measured and calculated (using double-diode model and the proposed MABC algorithm) currents and powers of the solar cell at 26 different working conditions
Full size table

Conclusions

In this paper, we modified the definition of scout bees in ABC algorithm to arrive at a more effective explanation of this algorithm called MABC. Moreover, despite all previous studies, we also took into account the output power of solar cell in definition of the objective function to be minimized for estimation. The various simulations presented in this paper and the comparisons made with real-world data proved that the proposed modifications can highly improve the accuracy and speed of algorithm.