Exact traveling wave solutions of some nonlinear evolution equations

Abstract

Using a traveling wave reduction technique, we have shown that Maccari equation, (2+1)-dimensional nonlinear Schrödinger equation, medium equal width equation, (3+1)-dimensional modified KdV–Zakharov–Kuznetsev equation, (2+1)-dimensional long wave-short wave resonance interaction equation, perturbed nonlinear Schrödinger equation can be reduced to the same family of auxiliary elliptic-like equations. Then using extended F-expansion and projective Riccati equation methods, many types of exact traveling wave solutions are obtained. With the aid of solutions of the elliptic-like equation, more explicit traveling wave solutions expressed by the hyperbolic functions, trigonometric functions and rational functions are found out. It is shown that these methods provide a powerful mathematical tool for solving nonlinear evolution equations in mathematical physics. A variety of structures of the exact solutions of the elliptic-like equation are illustrated.

Introduction

The effort in finding exact solutions to nonlinear equations is significant for the understanding of most nonlinear physical phenomena. For instance, the nonlinear wave phenomena observed in fluid dynamics, plasma, and optical fibers are often modeled by the bell-shaped sech solutions and the kink-shaped tanh solutions [1]. In recent years, there has been much interest in investigating different kinds of exact solutions of nonlinear evolution equations (NLEEs), such as soliton, negaton, peakon, complexiton, cuspon, rational, periodic, and quasiperiodic solutions. Exact solutions to nonlinear partial differential equations play an important role in nonlinear physical science since they can provide much physical information and more insight into the physical aspects of the problem and thus lead to further applications. In recent years, many methods for obtaining explicit traveling and solitary wave solutions of NLEEs have been proposed such as inverse scattering transform method [2], Darboux transformation method [3, 4], Hirota’s bilinear method [5], Bäcklund transformation method [6], homogeneous balance method [7], solitary wave ansatz method [8, 9], Jacobi elliptic function expansion method [10], the tanh function method [11], $(\frac{G^\prime}{G})$ expansion method [12, 13], F-expansion method [14], projective Ricatti equation method [15, 16, 17] and so on. Among them extended F-expansion and projective Ricatti equation methods have been proved to be a powerful mathematical tool to investigate the exact solutions for NLEEs. In the present paper, we will employ the extended F-expansion and projective Ricatti equation methods for solving the elliptic-like equation which is given as

$$ A\psi^{\prime\prime}+B\psi+D\psi^3=0, $$

(1)

where A,  B and D are arbitrary constants. This equation can also be written in more simplified form as

$$ \psi^{\prime\prime}+\alpha_1\psi+\alpha_3\psi^3=0, $$

(2)

with α₁ = B/A and α₃ = D/A. Equation (1) or its simplified form is one of the most important auxiliary equation, because many NLEEs can be converted to Eq. (1) using suitable transformations. The main step for solving the coupled systems lies in making a appropriate transformation to obtain the implicit relation between these two unknowns u and v as functions of third unknown ψ; then the system will be decoupled and the equation in ψ can be solved by the above foresaid methods. The rest of the paper is structured as follows: in “Description of methods” we give brief descriptions of extended F-expansion and projective Riccati equation methods; in “Traveling wave reduction of some nonlinear evolution equations”, a few NLEEs of physical interest are transformed into elliptic-like equations. In “The exact traveling wave solutions of elliptic-like equation”, we have obtained traveling wave solutions of elliptic-like equation using extended F-expansion and projective Riccati equation methods. In “Conclusions”, some conclusions are given.

Description of methods

The extended F-expansion method

We now describe the extended F-expansion method for NLEEs. We concisely show what is F-expansion method and how to use it to find various periodic wave solutions to nonlinear wave equations [14]. In this method a nonlinear partial differential equation (PDE)

$$ P(u,u_{t},u_{x},u_{y},u_{xt},u_{tt},u_{yt},u_{xx},\ldots)=0, $$

(3)

can be converted to a nonlinear ordinary differential equation (ODE)

$$ O(u,u^{\prime},u^{\prime\prime},u^{\prime\prime\prime},\ldots)=0, $$

(4)

upon using a wave variable ξ = λ₁x₁ + λ₂x₂ + λ₃x₃ + $\cdots$λ _l x _l  − ωt, so that u(x₁, x₂, x₃$\cdots$ , t) = u(ξ) and the localized wave solution u(ξ) travels with speed of ω. Now suppose that u(ξ) can be expanded as follows

$$ u(\xi)=\sum_{j=0}^{n}\sum_{i=0}^{j}c_{ji}F^{i}(\xi)G^{j-i}(\xi),\quad c_{nn}\neq 0, $$

(5)

or

$$ u(\xi)=a_0+\sum_{i=1}^{n}a_i F^i(\xi)+\sum_{j=1}^{n}b_j F^{-j}(\xi),\quad a_{n}\neq 0, $$

(6)

where c _ji ,  a₀,  a _i and b _j are constants to be determined, F(ξ) and G(ξ) satisfy the following relations

$$ {F^{\prime}}^2=P_1F^4+Q_1F^2+R_1, {G^{\prime}}^2=P_2G^4+Q_2G^2+R_2, $$

(7)

$$ G^2=\mu F^2+\nu, R_1=\frac{Q^2_1-Q^2_2+3P_2R_2}{3P_1},\; \mu=\frac{P_1}{P_2}, \; \nu=\frac{Q_1-Q_2}{3P_2}, \;\nu\neq0. $$

(8)

The integer n is determined by considering the homogeneous balance between the governing nonlinear terms and the highest order partial derivatives of u in nonlinear ODE Eq. (4).

Substituting Eqs. (5) or (6) into nonlinear ODE Eq. (4) and using Eqs. (7) and (8), we obtain a series in F^pG^q (p = 0, 1, 2, $\cdots$l; q = 0, 1) or (F^p, p = 0, 1, 2, $\cdots$l). Equating each coefficient of F^pG^q or (F^p) to zero yields a system of algebraic equations for c _ji  (j = 0, 1, 2, $\cdots$n; i = 0, $\cdots$ , j) and λ _i ,  ω, or (a _i , b _j  , i = 1, 2, $\cdots$n; j = 1, 2, $\cdots$n; λ _i , ω).

Now solving these equations by use of Mathematica, c _ij ,  λ _i and ω can be expressed in terms of P _i , Q _i , R _i ,  μ, ν and the parameters of nonlinear ODE Eq. (4). Substituting these results into Eqs. (5) or (6) gives the general form of traveling wave solutions (see “Appendix 1”).

With the aid of Appendices 1 and 2 and the relation Eqs. (7) and (8) the appropriate kinds of the Jacobi elliptic function solutions of Eq. (3) including the single functions and the combined function solutions can be chosen. As we know, when m → 1, Jacobi elliptic functions degenerate as hyperbolic functions and m → 0, Jacobi elliptic functions degenerate as trigonometric functions in the manner of “Appendix 1”. So we can get the corresponding hyperbolic function solutions and trigonometric function solutions.

The projective Riccati equation method

The well-known projective Riccati equations read as

$$ f^{'}(\xi)=pf(\xi)g(\xi), $$

(9)

$$ g^{\prime}(\xi)=R+pg^2(\xi)-rf(\xi), $$

(10)

where p ≠ 0 is a real constant, R and r are two real constants. The relation between f and g is

$$ g^2=-{p}\left[R-2rf+\frac{r^2+\delta}{R}f^2\right],\quad \delta=\pm1, \;R\neq 0. $$

(11)

Consider a given nonlinear PDE in the unknown u(x, y, z, $\cdots$ , t), which is a solution of ODE O(u, u^′, u″, $\cdots$ ) = 0, obtained by the traveling wave reduction $u(x, y, z, \ldots, t)\longrightarrow u(\xi = \lambda_1x + \lambda_2y + \lambda_3z + \cdots + \lambda_nt).$ Now we seek solutions of u(ξ) in the following form

$$ u(\xi)=\sum_{i=1}^nf^{i-1}(\xi)[A_if(\xi)+B_ig(\xi)]+A_0,\quad R\neq0, $$

(12)

where A _i and B _i are constants to be fixed later, and f(ξ) and g(ξ) are solutions of Eqs. (9) and (10). The parameter n in Eq. (12) can be determined by balancing the highest order partial derivative and nonlinear term in O(u, u^′, u^″, $\cdots$ ) = 0.

On substituting Eq. (12) along with conditions Eqs. (9)–(11) into ODE, and setting the coefficient of fⁱg^j (j = 0, 1, i = 0, 1, 2, 3, …) to zero yields a set of over determined algebraic equations, from which the constants A _i , B _i , R, r, and λ _i can be found explicitly.

According to [15, 16], the exact solutions of Eqs. (9) and (10) are of the form

Case 1 When p =  −1, δ = −1,  R ≠ 0

$$ f_1(\xi)=\frac{R\hbox{ sech}(\sqrt{R}\xi)}{r\hbox{ sech}(\sqrt{R}\xi)+1},\quad g_1(\xi)=\frac{\sqrt{R}\tanh(\sqrt{R}\xi)}{r\hbox{ sech}(\sqrt{R}\xi)+1}. $$

(13)

Case 2 When p =  −1, δ = 1,  R ≠ 0

$$ f_2(\xi)=\frac{R \hbox{ csch}(\sqrt{R}\xi)}{r\hbox{ csch}(\sqrt{R}\xi)+1},\quad g_2(\xi)=\frac{\sqrt{R}\coth(\sqrt{R}\xi)}{r\hbox{ csch}(\sqrt{R}\xi)+1}. $$

(14)

Case 3 When p = 1,  δ =  −1,  R ≠ 0

$$ f_3(\xi)=\frac{R\sec(\sqrt{R}\xi)}{r\sec(\sqrt{R}\xi)+1},\quad g_3(\xi)=\frac{\sqrt{R}\tan(\sqrt{R}\xi)}{r\sec(\sqrt{R}\xi)+1}, $$

(15)

$$ f_4(\xi)=\frac{R\csc(\sqrt{R}\xi)}{r\csc(\sqrt{R}\xi)+1},\quad g_4(\xi)=\frac{-\sqrt{R}\cot(\sqrt{R}\xi)}{r\csc(\sqrt{R}\xi)+1}. $$

(16)

Case 4 When R = r = 0

$$ f_5(\xi)=\frac{C}{\xi}=Cp g_{5}(\xi),\quad g_{5}(\xi)=\frac{1}{p\xi}, $$

(17)

where C is a constant. Substitute the constants A _i , B _i , R, r, and λ _i into Eq. (12) along with Eqs. (13)–(17) to obtain soliton and periodic (or rational) solutions of the nonlinear PDE of concern.

Traveling wave reduction of some nonlinear evolution equations

The (2+1)-dimensional Maccari system

In this paper, we are interested to reveal new exact traveling wave solutions for the following (2 + 1)-dimensional soliton equation

$$ iu_t+u_{xx}+uv=0, $$

(18a)

$$ v_t+v_y+(uu^*)_x=0, $$

(18b)

where u(x, y, t) is complex function and v(x, y, t) is real function. Eqs. (18a), (18b) is similar to integrable Zakharov equation in plasma physics to describe the behavior of sonic Langmuir solitons which are Langmuir oscillations trapped in regions of reduced plasma density caused by the ponderomotive force due to a high-frequency field [when x = y in Eq. (18b)]. Recently, Maccari [18] obtained Eqs. (18a), (18b) by an asymptotically exact reduction method based on Fourier expansion and spatiotemporal rescaling from the Kadomtsev–Petviashvili equation. The integrability property was explicitly demonstrated and Lax pairs were also obtained. Zhao [19] constructed some general traveling wave solutions of Maccari equation. Also, several periodic and soliton solutions of the above system have recently been reported [12, 20, 21]. Maccari’s system is a kind of NLEEs that are often presented to describe the motion of the isolated waves, localized in a small part of space, in many fields such as hydrodynamic, plasma physics, nonlinear optic, etc. To find some new exact solutions of Eqs. (18a) and (18b), we first introduce the following transformations

$$ u(x,y,t)=e^{i\eta}\psi(\xi),\quad v(x,y,t)=v(\xi), $$

(19a)

$$ \eta=kx+ly+\lambda t,\quad \xi=s(x+qy-2kt), $$

(19b)

where ψ(ξ) and v(ξ) are real functions, k,  l,  λ,  s and q are real constants. Substituting Eqs. (19a), (19b) into Eqs. (18a) and (18b), we have

$$ s^2\psi^{\prime\prime}(\xi)-(\lambda+k^2)\psi(\xi)+\psi(\xi)v(\xi)=0, $$

(20a)

$$ (q-2k)v^{\prime}(\xi)+(\psi^{2}(\xi))^{\prime}=0. $$

(20b)

To simplify ordinary differential Eqs. (20a) and (20b), integrating Eq. (20b), we have

$$ v(\xi)=\frac{1}{2k-q}\psi^{2}(\xi)+C_1, $$

(21)

where q ≠ 2k and C₁ is an integration constant. Substituting Eq. (21) into Eq. (20a), we obtain

$$ A\psi^{\prime\prime}(\xi)+B\psi(\xi)+D\psi^{3}(\xi)=0, $$

(22)

where $A=1, \,B=\frac{C_1-\lambda-k^2}{s^2}$ and $D=\frac{1}{s^2(2k-q)}.$ Thus, looking for exact solutions of Eq. (22) leads to finding explicit solutions of Eqs. (18a) and (18b) and latter is easier to solve than Eqs. (18a) and (18b). By applying the extended F-expansion and projective Riccati equation methods to Eq. (22), we can get some new exact traveling wave solutions of Eqs. (18a) and (18b).

The (2+1)-dimensional nonlinear Schrödinger system

We consider the coupled (2+1)-dimensional nonlinear system of Schrödinger equations as

$$ iu_t-u_{xx}+u_{yy}+|u|^2u-2uv=0, $$

(23)

$$ v_{xx}-v_{yy}-(|u|^2)_{xx}=0, $$

(24)

where u(x, y, t) and v(x, y, t) are complex-valued functions. Nonlinear PDE systems of the type given by Eqs. (23) and (24) play an important role in atomic physics, and the functions u and v have different physical meanings in different disciplines of physics [2, 22, 23]. Important applications are, for instance, in fluid dynamics [2] and plasma physics [22]. In the context of water waves, u is the amplitude of a surface wave packet while v is the velocity potential of the mean flow interacting with the surface waves [23]. However, in the hydrodynamic context, u is the envelope of the wave packet and v is the induced mean flow [2]. In addition, Eqs. (23) and (24) are relevant in a number of different physical contexts, describing slow modulation effects of the complex amplitude v, due to a small nonlinearity, or a monochromatic wave in a dispersive medium. To obtain the exact solutions of Eqs. (23) and (24), we use the transformations

$$ u(x,y,t)=\psi(\xi)\exp(i\eta), \quad v(x,y,t)=\phi(\xi), $$

(25)

$$ \xi= k(x + ly + 2(\alpha-\beta l)t),\quad \eta=\alpha x+\beta y+\gamma t. $$

(26)

where k, l, α, β and γ are constants to be determined. Note that ξ and η are traveling wave variables, not necessarily in the same direction. That is, ξ and η are independent linear functions of x,  y and t. Then ψ and ϕ are assumed to be rational functions of exp(ξ). When ψ is positive real, ψ is the modulus of the complex function u, and η is the argument. The modulus and argument are traveling waves but the two waves may be in different directions. From Eqs. (23) and (24), we may obtain the system of ODEs

$$ k^2(l^2-1)\psi^{\prime\prime} +(\alpha^2-\beta^2-\gamma)\psi+\psi^3-2\psi \phi=0, $$

(27)

$$ (l^2+1)\phi^{\prime\prime}+(\psi^2)^{\prime\prime}=0. $$

(28)

Integrating Eq. (28) with respect to ξ yields

$$ \phi=\frac{\psi^2}{l^2+1}+C_2, $$

(29)

where C₂ is an integration constant. Substituting Eq. (29) into Eq. (27), we obtain

$$ A\psi^{\prime\prime}+B\psi+D\psi^3=0, $$

(30)

where A = k²(l² − 1),  B = (α² − β² − γ − 2C₂) and $D=\frac{l^2-1}{l^2+1}.$ This equation can also be written in more simplified form as ψ′′ + α_1ψ + α_3ψ³ = 0, where $\alpha_1=\frac{\alpha^2-\beta^2-\gamma-2C_2}{k^2(l^2-1)}$ and $\alpha_3=\frac{l^2-1}{l^2+1}.$

Medium equal width equation

The medium equal width (MEW) equation is used as a model PDE for the simulation of one-dimensional wave propagation in nonlinear media with dispersion processes [24] and is given by

$$ u_t+3u^2u_x-au_{xxt}=0. $$

(31)

The MEW Eq. (31), which is related to the regularized long wave and KdV equation, has solitary waves with both positive and negative amplitudes, all of which have the same width. The MEW equation is a nonlinear wave equation with cubic nonlinearity with a pulse-like solitary wave solution. This equation appears in many physical applications and is used as a model for nonlinear dispersive waves. The equation gives rise to equal width undular bore. Using the wave variable ξ = x − vt converts Eq. (31) to an ODE

$$ vu+u^3+avu^{\prime\prime}=0, $$

(32)

which is obtained after integrating once and setting the constant of integration to zero.

The (2+1)-dimensional long wave-short wave resonance interaction equation

The nonlinear interaction of multiple waves results in several new physical developments [25]. The resonance interaction of long-wave with short-wave was first probed by Benney [26] for capillary-gravity waves in deep water. In this case simple interaction equations cannot be obtained, because for deep water waves there is no wave in the long wavelength limit. However, simple interaction equations can be realized in a stable stratified for oblique propagation of long and short-waves [27]. The single component two-dimensional long wave short wave resonance interaction (LSRI) equation for a two-layer fluid model has been derived in [28] using the multiple scale perturbation method and bright and dark type one and two-soliton solutions have been reported. Ohta et al. [29] derived the integrable two component analogue of the two-dimensional LSRI system as a governing equation for the interaction of the nonlinear dispersive waves by applying the reductive perturbation method. It has been shown in the two layer fluid model that resonance between the long-wave component and short-wave component takes place when the phase velocity of the former matches the group velocity of the latter [28]. This is a ubiquitous phenomenon which appears in hydrodynamics, bio-physics, plasma physics and in nonlinear optical systems. There exist many nonlinear wave equations in fluid mechanics, such as the KdV equation, the Boussinesq equation, the (2+1)-dimensional dispersive long wave equation in shallow water, etc. The (2+1)-dimensional LSRI equation can be written as

$$ S_{xx}-LS-i(S_t+S_y)=0 $$

(33)

$$ L_t-(2SS^{*})_x=0 $$

(34)

where L and S denote the long interfacial wave and the short surface wave packets, respectively, and S* is the complex conjugate of S. This system describes the long and short wave propagation at an angle to each other in a two-layer fluid. It has been shown that Eqs. (33) and (34) possess the bright and the dark double-soliton solutions, position and dromion solutions and coherent soliton structures. To solve Eqs. (33) and (34) by using our methods, we first reduce Eqs. (33) and (34) to a system of ODEs. We make the transformations

$$ S(x,y,t)=S(\xi)\exp(i\eta), \quad L(x,y,t)=L(\xi), $$

(35)

$$ \xi=\rho(x+ly-\chi t),\quad \eta=\alpha x+\beta y+\gamma t, $$

(36)

where ξ and η are real parameters and ρ,  l,  χ,  α,  β, and γ are constants. The substitution of Eqs. (35) and (36) into Eqs. (33) and (34) yields

$$ i\rho(2\alpha-\chi-l)e^{i\eta}\frac{{\rm d}S}{{\rm d}\xi}+\left(\rho^2\frac{{\rm d}^2S}{{\rm d}\xi^2}+(\beta+\gamma)S-SL\right)e^{i\eta}=0, $$

(37)

$$ \chi \frac{{\rm d}L}{{\rm d}\xi}-2\frac{{\rm d}^2S}{{\rm d}\xi^2}=0. $$

(38)

From Eq. (38) we get

$$ L=\frac{1}{\chi}(2S^2+C), $$

(39)

where C is the constant of integration. From Eq. (37) we have

$$ 2\alpha-\chi-l=0 \quad {\rm i.e}\quad \chi=2\alpha-l, $$

(40)

and

$$ \rho^2\frac{{\rm d}^2S}{{\rm d}\xi^2}+(\beta+\gamma)S-SL=0. $$

(41)

From Eqs. (39) and (41), we eliminate L and get

$$ \rho^2\frac{{\rm d}^2S}{{\rm d}\xi^2}+\left(\beta+\gamma-\frac{C}{\chi}\right)S-\frac{2}{\chi}S^3=0. $$

(42)

This equation can be converted into an elliptic like equation with $\alpha_1=\frac{(\beta+\gamma)\chi-{C}}{\chi \rho^2}$ and $\alpha_3=\frac{-2}{\chi \rho^2}$ and obtained exact solutions.

The (3+1)-dimensional modified KdV–Zakharov–Kuznetsev equation

Here, we consider the (3+1)-dimensional modified KdV–Zakharov–Kuznetsev equation given in the form as [30]

$$ u_t+\beta u^2 u_x+u_{xxx}+u_{xyy}+u_{xzz}=0, $$

(43)

where β is a nonzero constant. This equation transformed to elliptic-like equation using traveling wave transform u(x, y, z, t) = u(ξ), where ξ = x + y + z − vt. Here v is constant and permits us converting Eq. (43) into an ODE,

$$ 3u^{\prime\prime}+\frac{1}{3}\beta u^3-v u+C=0, $$

(44)

where C is a constant of integration and taken as zero for simplicity. This elliptic equation can be solved by F-expansion and projective Riccati equation methods.

Perturbed nonlinear Schrödinger equation

The nonlinear Schrödinger equation with its perturbation terms is given by [31]

$$ iu_t+\frac{1}{2}u_{xx}+F(|u|^2)u=i\epsilon R[u,u^*], $$

(45)

when R[u, u*] = 0, Eq. (45) reduces to the dimensionless nonlinear Schrödinger equation with non-Kerr law. If F(|u|²) = |u|² and R[u, u^*] = 0, Eq. (45) is the nonlinear Schrödinger equation with Kerr law. The first term represents the evolution term, the second term is the group velocity dispersion term. Here R is a spatio-differential or integro-differential operator while the perturbation parameter ε with 0 < ε < 1 is called the relative width of the the spectrum that arises due to quasi-monochromaticity and the perturbation terms are

$$ \begin{aligned} R\,&=\,\delta |u|^{2m}u+\alpha u_x+\beta u_{xx}-\gamma u_{xxx}+\lambda(|u|^2u)_x+\theta (|u|^2)_xu+\rho |u_x|^2u-i\xi (u^2u^*_x)_x\\ &\quad-i\eta u^2_xu^*-i\zeta u^*(u^2)_{xx}-i\mu((|u|^2)_xu)-i\chi u_{xxxx}-i\nu u_{xxxxx}+(\sigma_1u+\sigma_2u_x)\int\limits_\infty^x |u|^2 {\rm d}s \end{aligned} $$

(46)

In Eq. (46), δ is the coefficient of nonlinear damping or amplification depending on its sign and m could be 0, 1, 2. For m = 0,  δ is the linear amplification or attenuation according to δ being positive or negative. For m = 1,  δ represents the two-photon absorption (or a nonlinear gain if δ > 0). If m = 2,  δ gives a higher order correction (saturation or loss) to the nonlinear amplification-absorption. Also, β is the bandpass filtering term. In Eq. (46), λ is the self-steepening coefficient for short pulses (typically <100 fs), γ is the higher order dispersion coefficient. Here μ is the coefficient of Raman scattering and α is the frequency separation between the soliton carrier and the frequency at the peak of EDFA gain. Moreover, ρ represents the coefficient of nonlinear dissipation induced by Raman scattering. The coefficients of ξ,  η and ζ arise due to quasi-solitons. The integro-differential perturbation terms with σ₁ and σ₂ are due to saturable amplifiers. The coefficients of the higher order dispersion terms are, respectively, given by γ,  χ and ν. It is known that the NLSE, as given by Eq. (45), does not give correct prediction for pulse widths smaller than 1 ps. For example, in solid state solitary lasers, where pulses as short as 10 fs are generated, the approximation breaks down. Thus, quasi-monochromaticity is no longer valid and so higher order dispersion terms come in. If the GVD is close to zero, one needs to consider the third and higher order dispersion for performance enhancement along trans-oceanic and transcontinental distances. Also, for short pulse widths where GVD changes, within the spectral bandwidth of the signal cannot be neglected, one needs to take into account the presence of higher order dispersion terms. This reasoning leads to the inclusion of the fourth and sixth order dispersion terms that are, respectively, given by the coefficients of χ and ν. In this paper we study the dimensionless form of the perturbed NLSE with Kerr law nonlinearity, which is the special case of Eq. (45) and given as

$$ iu_t+u_{xx}+\alpha |u|^2u+i[\gamma_1u_{xxx}+\gamma_2|u|^2u_x+\gamma_3(|u|^2)_xu]=0, $$

(47)

where γ₁ is the third order dispersion, γ₂ is the nonlinear dispersion, while γ₃ is also a version of nonlinear dispersion. Since u = u(x, t) is a complex function, we assume that Eq. (47) has traveling wave solutions in the form

$$ u(x,t)=\psi(\xi)\exp(i(\Uptheta x-\Upomega t)), \quad \xi=k(x-ct), $$

(48)

where $\Uptheta, \,\Upomega, \,k$ and c are arbitrary constants to be determined. Substituting Eq. (48) into Eq. (47) and separating the real and imaginary parts, we have

$$ k^2(1-3\gamma_1 \Uptheta)\psi^{\prime\prime}+(\Upomega-\Uptheta^2+\gamma_1\Uptheta^3)\psi+(\alpha-\gamma_2 \Uptheta)\psi^3=0, $$

(49)

$$ \gamma_1 k^2 \psi^{\prime\prime\prime}-(c-2\Uptheta+3\gamma_1 \Uptheta^2)\psi^{\prime}+(\gamma_2+2\gamma_3)\psi^2 \psi^{\prime}=0. $$

(50)

Integrating Eq. (50) with respect to ξ once and setting the integration constant to be zero, then we have

$$ \gamma_1k^2\psi^{\prime\prime}+(2\Uptheta-c-3\gamma_1 \Uptheta^2)\psi^{\prime}+\left(\frac{1}{3}\gamma_2+\frac{2}{3}\gamma_3\right)\psi^3=0. $$

(51)

The necessary and sufficient condition for a non-constant function ψ = ψ(ξ) satisfying both Eqs. (49) and (51) is that the coefficients of Eqs. (49) and (51) satisfying the proportional ratio are as follows:

$$ \frac{\gamma_1}{1-3\gamma_1 \Uptheta}=\frac{2\Uptheta-c-3\gamma_1 \Uptheta^2}{\Upomega-\Uptheta^2+\gamma_1\Uptheta^3}=\frac{\frac{1}{3}\gamma_2+\frac{2}{3}\gamma_3}{\alpha-\gamma_2 \Uptheta} $$

(52)

For the sake of simplicity we set $A=\gamma_1k^2, \,B=2\Uptheta-c-3\gamma_1 \Uptheta^2$ and $D=\frac{1}{3}\gamma_2+\frac{2}{3}\gamma_3,$ then the Eqs. (51) can be written as

$$ A\psi^{\prime\prime}(\xi)+B\psi(\xi)+D\psi^{3}(\xi)=0. $$

(53)

The exact traveling wave solutions of elliptic-like equation

Using extended F-expansion method

Considering the homogeneous balance between ψ″(ξ) and ψ³(ξ) in Eq. (1), we assume that ψ(ξ) can be expanded by the extended F-expansion in the following form

$$ \psi(\xi)=a_0+a_1F(\xi)+b_1G(\xi), $$

(54)

where a₀,  a₁ and b₁ are constants to be determined later, F(ξ) and G(ξ) satisfy the relations Eqs. (7) and (8). Substituting Eq. (54) into Eq. (22) along with Eqs. (7) and (8), collecting the coefficients of the FⁿG^m(n = 0, 1, 2, 3; m = 0, 1) and setting them to zero, we get a system of algebraic equations:

$$ F^0: a_0B+a^3_0D+3a_0\nu b^2_1D=0, $$

(55)

$$ F: a_1B+3a^2_0a_1D+3a_1\nu b^2_1D+a_1AQ_1=0, $$

(56)

$$ G: b_1B+3a^2_0b_1D+\nu b^3_1 D+b_1AQ_2+2\nu b_1 AP_2=0, $$

(57)

$$ F^2: 3a_0a^2_1D+3\mu a_0b^2_1D=0, $$

(58)

$$ FG: 6a_0a_1b_1=0, $$

(59)

$$ F^2G: b_1a^2_1BD+\mu b^3_1D+2\mu b_1AP_2=0, $$

(60)

$$ F^3: a^3_1D+3\mu a_1b^2_1D+2a_1AP_1=0. $$

(61)

On solving the above system of algebraic equations with symbolic computations, we obtain following two kinds of solutions.

Case 1

$$ a_0=0,\quad a_1=\pm\sqrt{\frac{-2AP_1}{D}},\quad b_1=0, $$

(62)

the following constraint among the coefficients A and B of Eq. (22) should be respected B + AQ₁ = 0.

Case 2

$$ a_0=0, \quad a_1=\pm\sqrt{\frac{-AP_1}{2D}}, \quad b_1=\pm\sqrt{\frac{-AP_1}{2\mu D}}. $$

(63)

For this case, the following constraint among the coefficients A and B of Eq. (22) has been obtained 2Bμ + A(2μQ₁ − 3νP₁) = 0. On substituting Eq. (62) into Eq. (54), we obtain the following traveling wave solutions as

$$ \psi^{sj}(\xi)=\pm \sqrt{\frac{-2P_1A}{D}}F(\xi), $$

(64)

where the superscript sj means single Jacobi, A and D should verify constraint relation. These solutions are the single nondegenerative Jacobi elliptic function solutions. The relations between values of (R₁, Q₁, P₁) and the corresponding Jacobi elliptic function F(ξ) of Eqs. (7), (8) are given in “Appendix 1”. Substituting the values of (R₁, Q₁, P₁) and the corresponding Jacobi F(ξ) chosen from “Appendix 1” into the general form of the traveling solution Eq. (64), we can simultaneously obtain different periodic wave solutions to the elliptic-like Eq. (1).

For example if we choose R₁ = 1,  Q₁ =  −(1 + m²),  P₁ = m², then F(ξ) = sn(ξ), thus

$$ \psi(\xi)=\pm m\sqrt{\frac{-2A}{D}}F(\xi), $$

(65)

where AD < 0,  B = (1 + m²)A.

Substituting Eq. (63) into Eq. (54) we obtain the combined nondegenerative Jacobi elliptic function solutions,

$$ \psi^{cj}(\xi)=\pm \sqrt{\frac{-P_1A}{2\mu D}}\Big[\sqrt{\mu}F(\xi)+ \epsilon G(\xi)\Big], $$

(66)

where the superscript cj means combined Jacobi, ε =  ±1,  P₁A/D < 0,  μ > 0,  A and B should verify constraint relation. With the aid of “Appendix 2”, if we select dn²(ξ) = m²cn²(ξ) + (1 − m²), and set

$$ F(\xi)=cn(\xi), G(\xi)=dn(\xi),\, \mu=m^2, \,\nu=1-m^2, $$

(67)

and from “Appendix 2”, we find that the respective coefficients of nonlinear ODE for cn(ξ) and dn(ξ) are

$$ P_1=-m^2, Q_1=2m^2-1, Q_2=2-m^2 $$

(68)

Inserting Eqs. (67) and (68) into Eq. (66) we have

$$ \psi_1^{cj}(\xi)=\pm \sqrt{\frac{-A}{2 D}}[m cn(\xi)+ \epsilon dn(\xi)]. $$

(69)

In the same manner with the aid of Appendices 1 and 2 as mentioned above, we can obtain the following solutions

$$ \psi_2^{cj}(\xi)=\pm \sqrt{\frac{-(1-m^2)A}{2 D}}[m sd(\xi)+ \epsilon nd(\xi)]. $$

(70)

$$ \psi_3^{cj}(\xi)=\pm \sqrt{\frac{-(1-m^2)A}{2 D}}[m sc(\xi)+ \epsilon nc(\xi)]. $$

(71)

$$ \psi_4^{cj}(\xi)=\pm \sqrt{\frac{-A}{2 D}}[m cs(\xi)+ \epsilon ds(\xi)]. $$

(72)

$$ \psi_5^{cj}(\xi)=\pm \sqrt{\frac{-A}{2 D}}[\sqrt{(1-m^2)} nc(\xi)+ \epsilon dc(\xi)]. $$

(73)

$$ \psi_6^{cj}(\xi)=\pm \sqrt{\frac{-A}{2 D}}\left[\sqrt{(1-m^2)} sc(\xi)+ \epsilon dc(\xi)\right], $$

(74)

where ε = ±1,  AD < 0,  B = −(1 − 2m²)A/2. Similarly, by choosing P _i ,  Q _i and R _i from “Appendix 1”, one can get many other families of solutions in terms of JEFs. However, for the limit of length of paper, we omit them here.

Using projective Riccati equations method

Considering the homogeneous balance between ψ^″(ξ) and ψ³(ξ) in Eq. (2), the solution of Eq. (2) is written as

$$ \psi(\xi)=A_0+A_1f(\xi)+B_1g(\xi), $$

(75)

where A₀,  A₁ and B₁ are constants to be determined later and f(ξ) and g(ξ) satisfy Eqs. (9)–(11). Substituting Eq. (75) into Eq. (22) and making use of Eqs. (9)–(11), becomes a polynomials for fⁱ (i = 0, 1, 2, 3) and f^jg(j = 0, 1, 2), setting the coefficients of the polynomials to zero yields a set of algebraic equations.

$$ {\rm const}: \alpha_1A_0+\alpha_3A^3_0-3\alpha_3pB^2_1R=0, $$

(76)

$$ f(\xi): -pA_1R+\alpha_1A_1+3\alpha_3A^2_0A_1+6\alpha_3prA_0B^2_1-3\alpha_3pA_1B^2_1R=0, $$

(77)

$$ g(\xi): \alpha_1B_1+3\alpha_3A^2_0B_1-\alpha_3pB^3_1R=0, $$

(78)

$$ f^2(\xi): 3prA_1+\alpha_3\left\{3A_0A^2_1+6prA_1B^2_1-3pA_0B^2_1\left(\frac{r^2+\delta}{R}\right)\right\}=0, $$

(79)

$$ f(\xi)g(\xi): prB_1+6\alpha_3A_0A_1B_1+2\alpha_3prB^3_1=0, $$

(80)

$$ f^3(\xi): \alpha_3\left\{A^3_1-3pA_1B^2_1\left(\frac{r^2+\delta}{R}\right)\right\}-2pA_1\left(\frac{r^2+\delta}{R}\right)=0, $$

(81)

$$ f^2(\xi)g(\xi): \alpha_3\left\{3A^2_1B_1-pB^3_1\left(\frac{r^2+\delta}{R}\right)\right\}-2pB_1\left(\frac{r^2+\delta}{R}\right)=0. $$

(82)

From above set of equations, using the Wu elimination method [32], we have the following solutions:

• 1. $A_0=A_1=r=0, B^2_1=-\frac{2}{\alpha_3}, R=-\frac{\alpha_1}{2p},p=\pm 1,\delta=\pm 1,$

• 2. $A_0=B_1=r=0, A^2_1=-\frac{2\delta}{\alpha_1\alpha_3}, R=-\frac{\alpha_1}{p},p=\pm 1,\delta=\pm 1,$

• 3. $A_0=0, A^2_1=-\frac{r^2+\delta}{4\alpha_1\alpha_3}, B^2_1=-\frac{1}{2\alpha_3}, R=-\frac{2\alpha_1}{p},p=\pm 1,\delta=\pm 1.$

Therefore we obtain 16 kinds of exact solutions of elliptic-like equation.

Case 1 Dark soliton solutions

$$ \psi_1(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}} \tanh \left(\sqrt{\frac{\alpha_1}{2}}\xi\right), \quad \alpha_1>0, \alpha_3<0. $$

(83)

Case 2 Singular dark soliton solutions

$$ \psi_2(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}} \coth \left(\sqrt{\frac{\alpha_1}{2}}\xi\right), \quad \alpha_1>0, \alpha_3<0. $$

(84)

Case 3 Bright soliton solutions

$$ \psi_3(\xi)=\pm \sqrt{-\frac{2}{\alpha_3}} \hbox{ sech} (\sqrt{{-\alpha_1}}\xi), \quad \alpha_1<0, \alpha_3<0. $$

(85)

Case 4 Formal soliton solutions

$$ \psi_4(\xi)=\pm \sqrt{\frac{2}{\alpha_3}} \hbox{ csch} (\sqrt{{-\alpha_1}}\xi), \quad \alpha_1<0, \alpha_3>0. $$

(86)

Case 5 Periodic wave solutions

$$ \psi_5(\xi)=\pm \sqrt{\frac{\alpha_1}{\alpha_3}} \tan \left(\sqrt{-\frac{\alpha_1}{2}}\xi\right), \quad \alpha_1<0, \alpha_3<0. $$

(87)

Case 6 Periodic wave solutions

$$ \psi_6(\xi)=\pm \sqrt{\frac{\alpha_1}{\alpha_3}} \cot \left(\sqrt{-\frac{\alpha_1}{2}}\xi\right), \quad \alpha_1<0, \alpha_3<0. $$

(88)

Case 7 Periodic wave solutions

$$ \psi_7(\xi)=\pm \sqrt{-\frac{2}{\alpha_3}} \sec (\sqrt{{\alpha_1}}\xi), \quad \alpha_1>0, \alpha_3<0. $$

(89)

Case 8 Periodic wave solutions

$$ \psi_8(\xi)=\pm \sqrt{-\frac{2}{\alpha_3}} \hbox{ csch} (\sqrt{{\alpha_1}}\xi), \quad \alpha_1>0, \alpha_3<0. $$

(90)

Case 9 Combined formal soliton like solutions

$$ \psi_9(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\left[\frac{\sqrt{r^2-1}\hbox{ sech} (\sqrt{2\alpha_1}\xi)}{r \hbox{ sech} (\sqrt{2\alpha_1}\xi)+1}+\frac{p\tanh (\sqrt{2\alpha_1}\xi)}{r \hbox{ sech} (\sqrt{2\alpha_1}\xi)+1}\right], \quad \alpha_1>0, \alpha_3<0. $$

(91)

Case 10 Combined formal soliton like solutions

$$ \psi_{10}(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\left[\frac{\sqrt{r^2+1}\hbox{ csch} (\sqrt{2\alpha_1}\xi)}{r \hbox{ csch} (\sqrt{2\alpha_1}\xi)+1}+\frac{p\coth (\sqrt{2\alpha_1}\xi)}{r \hbox{ csch} (\sqrt{2\alpha_1}\xi)+1}\right], \quad \alpha_1>0, \alpha_3<0. $$

(92)

Case 11 Combined formal periodic wave like solutions

$$ \psi_{11}(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\left[\frac{\sqrt{1-r^2}\sec (\sqrt{-2\alpha_1}\xi)}{r \sec (\sqrt{-2\alpha_1}\xi)+1}+\frac{p\tan (\sqrt{-2\alpha_1}\xi)}{r \sec (\sqrt{-2\alpha_1}\xi)+1}\right], \quad \alpha_1<0, \alpha_3>0. $$

(93)

Case 12 Combined formal periodic wave like solutions

$$ \psi_{12}(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\left[\frac{\sqrt{1-r^2}\csc (\sqrt{-2\alpha_1}\xi)}{r \csc (\sqrt{-2\alpha_1}\xi)+1}+\frac{p\cot (\sqrt{-2\alpha_1}\xi)}{r \csc (\sqrt{-2\alpha_1}\xi)+1}\right], \quad \alpha_1<0, \alpha_3>0. $$

(94)

Case 13 New soliton solutions

$$ \psi_{13}(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\frac{\tanh (\sqrt{2\alpha_1}\xi)}{r \hbox{ sech} (\sqrt{2\alpha_1}\xi)+1}, \quad \alpha_1>0, \alpha_3<0. $$

(95)

Case 14 New periodic wave solutions

$$ \psi_{14}(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\frac{\tan (\sqrt{-2\alpha_1}\xi)}{r \sec (\sqrt{-2\alpha_1}\xi)+1}, \quad \alpha_1<0, \alpha_3>0. $$

(96)

Case 15 New periodic wave solutions

$$ \psi_{15}(\xi)=\pm \sqrt{-\frac{\alpha_1}{\alpha_3}}\frac{\cot (\sqrt{-2\alpha_1}\xi)}{r \csc (\sqrt{-2\alpha_1}\xi)+1}, \quad \alpha_1<0, \alpha_3>0. $$

(97)

Case 16 Rational solutions

$$ \psi_{16}(\xi)=\pm \sqrt{-\frac{2}{\alpha_3}}\frac{1}{\xi}, \quad \alpha_3>0 $$

(98)

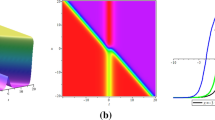
where α₁ = 0. So, one can obtain the full set of exact solutions of NLEEs by substituting the various solutions of elliptic like equations into original NLEEs. In Fig. 1 we shows the 2-dimensional profile plots of some of the solutions.

Fig. 1

a A kink type dark solitary wave solution with α₁ = 2 and α₃ =  −1. b A bell type solitary wave solution with α₁ =  −2 and α₃ = −1. c, d represents periodic wave solutions at α₁ = 2 and α₃ = −1. e A combined formal soliton solution with α₁ = 2,  α₃ = −1, r = 2, and p = 1. f A combined formal periodic wave solution with α₁ = −2,  α₃ = 1, r = 0.5, and p = 1

Conclusions

In this work, we apply extended F-expansion method and projective Riccati equation method to obtain the single and combined generalized solutions of nonlinear wave equations. Many different new forms of traveling wave solutions such as periodic wave solution, solitary wave solution or bell-shaped soliton solutions and shock wave solution or kink-shaped soliton solutions are obtained. These results have proven that extended F-expansion method and projective Riccati equation method are reliable and efficient in handling nonlinear problems. Considering the utility of these equations in plasma and hydrodynamics and other branches of physics, these solutions may find practical applications. These methods can be applied to solve other systems of nonlinear differential equations.

Appendices

Appendix 1

Table of Jacobi elliptic functions

Solution	R	Q	P	F(ξ)	m = 0	m = 1
1	1	−(1 + m2)	m 2	sn	$\sin$	$\tanh$
2	1 − m2	2m2 − 1	−m2	cn	$\cos$	sech
3	m2 − 1	2 − m2	−1	dn	1	sech
4	m 2	−(1 + m2)	1	ns	cosec	$\coth$
5	−m2	2m2 − 1	1 − m2	nc	$\sec$	$\cosh$
6	−1	2 − m2	m2 − 1	nd	1	$\cosh$
7	1	2 − m2	1 − m2	sc	$\tan$	$\sinh$
8	1 − m2	2 − m2	1	cs	$\cot$	cosech
9	1	−(1 + m2)	m 2	cd	$\cos$	1
10	m 2	−(1 + m2)	1	dc	$\sec$	1

Appendix 2

Jacobi elliptic functions with modulus 0 < m < 1 have the identity in the form G² = μF² + ν$cn^2(\xi)=-sn^2(\xi)+1, \quad dn^2(\xi)=-m^2 sn^2(\xi)+1,\quad cd^2(\xi)=-\frac{(m^2-1)}{m^2} nd^2(\xi)+\frac{1}{m}, \,cd^2(\xi)=-(m^2-1)sd^2(\xi)+1,$dn²(ξ) = m²cn²(ξ) + (1 − m²),  nd²(ξ) = −m²sd²(ξ) + 1, ns²(ξ) = cs²(ξ) + 1,   nc²(ξ) = sc²(ξ) + 1,  dc²(ξ) = (1 − m²)nc²(ξ) + m²,   dc²(ξ) = (1 − m²)sc²(ξ) + 1.