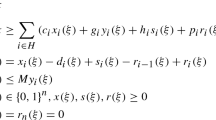Robust Wagner–Whitin algorithm with uncertain costs

Abstract

In real-world applications, costs for products are not deterministic: neither static nor dynamic. They actually tend to be non-stationary and cross-correlated. To overcome this drawback, there have been some efforts by researchers to extend the Wagner–Whitin algorithm to consider stochastic costs. However, they assume that the information of probability density function of random costs exists. This paper applied a robust approach in reformulating the uncertain lot-sizing problem and used the Wagner–Whitin algorithm to find an optimal solution of its robust counterpart. The solution of the proposed algorithm in an example from the literature is compared with the classical one.

Introduction and literature review

Lot sizing has been in question since the beginning of industrialization. It aims to answer two questions in the area of inventory control: when to order and how much to order. The first question is also known as the reorder point and the second one is the size of the ordered lot. To put it another way, the lot-sizing problem wants to find a balance between the setup costs vs. inventory holding costs. Harris was the first one to attack this problem and introduced economic order quantity (EOQ) (Harris 1915). In the EOQ model, which provides us with an optimal lot size, the demands are constant in the infinite planning horizon. Later, Wilson found order points by the means of a statistical approach and could popularize the EOQ model (Wilson 1934).

Contradictory to the conditions of EOQ, when the parameters such as demands or costs of production are dynamic in a finite planning horizon, the EOQ model gives us deceptive results (Grewal 1999) and therefore a new solution is required. We know that in real-world applications, it rarely happens that the demands or costs stay constant in an infinite time horizon. It is more logical if we consider dynamic demands or costs in a finite time horizon. Wagner and Whitin (1958), as the pioneers, tackled such a lot-sizing problem. Their algorithm gives us the optimal solution for lot sizing through dynamic programming. Wagner–Whitin algorithm is useful for problems with deterministic and dynamic demands and costs. The computational complexity of this classic algorithm is O(t²)—where t is the time horizon (Hoesel and Wagelmans 1990; Brahimi et al. 2017). In Wagner–Whitin algorithm, the following assumptions exist (Johnson and Montgomery 1974): The planning horizon is finite and no shortages are allowed. Furthermore, the initial and final inventory levels ought to be zero and a single lot may be procured in each period. In 2004, Wagner claimed that this algorithm has been so useful since its publication in 1958 (Wagner 2004). Other solutions to the lot-sizing problem include some improvements to Wagner–Whitin algorithm, heuristic methods, linear programming, integer programming, fuzzy logic, etc. For more information, the reader is referred to Singh (1992) and Grewal (1999).

Contradictory to the initial conditions of the EOQ model and the Wagner–Whitin algorithm, in real-world applications, the demands or costs of production are not deterministic: neither static nor dynamic. They actually tend to be stochastic and probabilistic (Şenyiğit et al. 2013). To overcome this drawback, there have been some efforts by researchers to extend the Wagner–Whitin algorithm to fit stochastic situations. Vargas (2009) presented the stochastic version of the Wagner–Whitin algorithm with stochastic and time-varying demands. He also investigated the Wagner–Whitin algorithm when the density function of the demand is known. His algorithm, similar to Wagner–Whitin’s, gives us an optimal solution. In addition, Fleischhacker and Zhao (2011) extended the Wagner–Whitin algorithm to include the risk of failure in demands and therefore they could transform it into a stochastic production-inventory model.

There are also other heuristic and meta-heuristic methods for dealing with lot-sizing problems in the presence of stochastic demands or costs. For instance, Manikas et al. (2009) and Şenyiğit and Erol (2010) simulated lot-sizing problem when both demands and costs are uncertain and stochastic. Piperagkas et al. (2012) also used three nature-inspired heuristics to tackle the dynamic lot-sizing problem under stochastic and stationary demands. Moreover, meta-heuristic algorithms are other methods for dealing with stochastic variables in lot-sizing problem. As an example, Şenyiğit et al. (2013) have trained different artificial neural networks with genetic algorithm and bee algorithm. They have then used these neural networks in studying the lot-sizing problem when costs and demands are stochastic. For a review on the use of genetic algorithms and artificial neural networks in the stochastic dynamic lot-sizing problem, refer to Goren et al. (2010) and Radzi et al. (2000), respectively. In addition, Winands et al. (2011) reviewed different models concerning stochastic lot-sizing problem.

One of the sources for future estimation of uncertain parameters such as cost is historical data. According to the above literature, information about uncertain parameters lies into two groups. Firstly, we may have probabilistic information about random costs in which in this case we have probability density function (pdf) of the random parameter. It is common to use stochastic programming when the pdf exists. Secondly, we do not have information about pdf and the only information about random costs is its moments like the mean and covariance. The second case can be categorized into two groups, namely stationary and non-stationary. Stationary refers to the case that the moments will not change during the planning time horizon, while in the non-stationary case, moments will change from time to time during the planning time horizon.

From a practical viewpoint, the parameters of the lot-sizing problem such as costs and demands are random and thus not deterministic. This is the most important weak point of the deterministic methods. In addition, as far as the stochastic methods are concerned, their main drawback is that they are dependent on a known probabilistic distribution. However, the proposed method of this paper does not assume to have any information about the pdf of random costs and the only required information is the covariance matrix and the mean value vector of the historical data of costs.

Here, we use a robust approach to deal with uncertain costs with non-stationary moments in a lot-sizing problem. Deviations of uncertain costs are postulated in a closed and convex space, namely U. The covariance matrix and the mean value vector of the costs calculated on the historical data are used to formulate the uncertainty region. The uncertainty region U is a unit ball centered by a nominal (mean) value of the uncertain parameter. Radius of the uncertainty region changes by exerting coefficient r, according to the expected risk for the decision maker. The meaning of the unit ball differs in various structures defined by norms, and the appropriate norm is chosen (Hanafizadeh and Seifi 2004). Such uncertainty region can be considered for all uncertain parameters such as costs, demands, lead time and so forth. However, in this study, the uncertainty has been considered only for future costs to keep the formula simple. After determining the uncertainty region, considering the worst-case behavior for uncertain costs in the U uncertainty region, the robust counterpart of a lot-sizing problem is developed. Robust formula of the objective function and the constraint of the lot-sizing problem are used inside the classical Wagner–Whitin algorithm to find an optimal solution for its robust counterpart. Therefore, in this article, an extension of Wagner–Whitin algorithm is considered as the so-called robust algorithm. After that, an analysis is done on the robust relations to find out what happens if some parameters of the relations vary. The next step is to solve an example from the literature and use the robust approach versus the classical Wagner–Whitin algorithm in finding the optimal solution. It is noteworthy that the robust algorithm offers an optimal solution for the robust counterpart of the lot-sizing model, while the classical Wagner–Whitin algorithm offers an optimal solution for the lot-sizing problem with nominal value of costs.

In Sect. 1, we expand the Wagner–Whitin algorithm when costs are uncertain and correlated with each other. Then, the new robust extension is analyzed in Sect. 2 and in Sect. 3 the application of the proposed method is depicted through solving an example from the literature. The example is solved by both the proposed robust method and the classical Wagner–Whitin algorithm, and the results are compared to each other. In addition, the reader can find the conclusion and then the limitations and future studies in Sect. 4.

Robust Wagner–Whitin algorithm with uncertain costs

In this paper, small bold italic letters and capital bold letters are used to delineate vectors and matrices, respectively. In addition, numbers are illustrated by small italic letters.

In the robust approach, the variations of the uncertain parameters are postulated in a continuous, closed, convex, bounded and non-null region. The concept of norm function is applied to make U uncertainty region (Hanafizadeh and Seifi 2004). This article applies to distributions whose contours can be approximated by a convex norm body. The following relationship exists for l₁, l₂ and l_∞ norm bodies (Boyd and Vandenberghe 2004):

$$l_{q} - {\text{norm body}} = \{ {\mathbf{u}}\varepsilon R^{\left( n \right)} |\left\| {\mathbf{u}} \right\|_{q} \le r\}$$

(1)

$${\text{where}}\quad \left\| {\mathbf{u}} \right\|_{1} \ge \left\| {\mathbf{u}} \right\|_{2} \ge \left\| {\mathbf{u}} \right\|_{\infty }$$

Small letter u is a vector variable indicating perturbation of the uncertain cost, and it falls within $l_{q} - {\text{norm body}}$ region.

Now, starting with the Wagner–Whitin algorithm, the standard equations to calculate the price of the minimum cost program for periods 1 to k, when the inventory level at period k is zero, are (Wagner and Whitin 1958):

$$f_{k} = \mathop {\hbox{min} }\limits_{0 \le j < k} \left[ {f_{j} + m_{jk} } \right]$$

(2)

$$m_{jk} = a_{j + 1} + c_{j + 1} b_{j + 1} + \mathop \sum \limits_{t = j + 1}^{k - 1} h_{t} \mathop \sum \limits_{r = t + 1}^{k} d_{r}$$

(3)

where f_k is the minimum cost program for period 1 to period k when inventory level at period k is zero.

m_jk is the cost incurred in periods j + 1 through k.

a_j+1 is the fixed cost if an order is made in period j + 1.

c_j+1 is the cost of producing each unit in period j + 1.

b_j+1 is the number of units produced/bought in period j + 1.

h_t is the cost of keeping a produced unit in the warehouse from period t to period t + 1.

d_r is the estimated demand for period r.

Subject to:

$$l_{t - 1} + b_{t} = d_{t} + l_{t}$$

(4)

and l_t is the inventory level at period t.

Here, we write relation (5) in vector form:

$$\begin{aligned} m_{jk} & = \left( {\begin{array}{*{20}c} {a_{j + 1} } \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right)^{T} \left( {\begin{array}{*{20}c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} } \right) + c_{j + 1} \left( {\mathop \sum \limits_{i = j + 1}^{k} d_{i} } \right) + \mathop \sum \limits_{t = j + 1}^{k - 1} h_{t} \mathop \sum \limits_{r = t + 1}^{k} d_{r} \\ & = \left( {\varvec{a}^{{\varvec{jk}}} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + c_{j + 1} \left( {d_{j + 1} + d_{j + 2} + \cdots + d_{k} } \right) + \left( {\begin{array}{*{20}c} {h_{j + 1} } \\ {h_{j + 1} } \\ \vdots \\ {h_{j + 1} } \\ \end{array} } \right)^{T} \left( {\begin{array}{*{20}c} {d_{j + 2} } \\ {d_{j + 3} } \\ \vdots \\ {d_{k} } \\ \end{array} } \right) \\ & \quad + \left( {\begin{array}{*{20}c} {h_{j + 2} } \\ {h_{j + 2} } \\ \vdots \\ {h_{j + 2} } \\ \end{array} } \right)^{T} \left( {\begin{array}{*{20}c} {d_{j + 3} } \\ {d_{j + 4} } \\ \vdots \\ {d_{k} } \\ \end{array} } \right) + \cdots + \left( {h_{k - 1} } \right)^{T} \left( {d_{k} } \right) \\ & = \left( {\varvec{a}^{{\varvec{jk}}} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + \left( {\begin{array}{*{20}c} {c_{j + 1} } \\ {c_{j + 1} } \\ \vdots \\ {c_{j + 1} } \\ \end{array} } \right)^{T} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{j + 1} } \\ {d_{j + 2} } \\ \vdots \\ \end{array} } \\ {d_{k} } \\ \end{array} } \right) + \left( {\varvec{h}^{{\varvec{j}\text{ + }\varvec{1,k}}} } \right)^{T} \varvec{d}^{{\varvec{j}\text{ + }\varvec{1,k}}} + \left( {\varvec{h}^{{\varvec{j}\text{ + }\varvec{2,k}}} } \right)^{T} \varvec{d}^{{\varvec{j} + {\mathbf{2,}}\varvec{k}}} + \cdots \\ & \quad + \left( {\varvec{h}^{{\varvec{k}\text{ - }\varvec{1,k}}} } \right)^{T} \varvec{d}^{{\varvec{k}\text{ - }\varvec{1,k}}} \\ & = \left( {\varvec{a}^{{\varvec{jk}}} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + (\varvec{c}^{{\varvec{jk}}} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} + \mathop \sum \limits_{t = j + 1}^{k - 1} \left( {\left( {\varvec{h}^{{\varvec{tk}}} } \right)^{T} \varvec{d}^{{\varvec{tk}}} } \right) \\ \end{aligned}$$

(5)

where

$$\varvec{a}^{{\varvec{jk}}} = \left. {\left( {\begin{array}{*{20}c} {a_{j + 1} } \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right)} \right\}\left( {k - j} \right){\text{times}}$$

$$\varvec{e}^{{\varvec{jk}}} = \left. {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} } \right)} \right\}\left( {k - j} \right){\text{times}}$$

$$\varvec{c}^{{\varvec{jk}}} = \left. {\left( {\begin{array}{*{20}c} {c_{j + 1} } \\ {c_{j + 1} } \\ \vdots \\ {c_{j + 1} } \\ \end{array} } \right)} \right\}\left( {k - j} \right){\text{times}}$$

$$\varvec{h}^{{\varvec{tk}}} = \left. {\left( {\begin{array}{*{20}c} {h_{t} } \\ {h_{t} } \\ \vdots \\ {h_{t} } \\ \end{array} } \right)} \right\}\left( {k - t} \right){\text{times}}$$

$$\varvec{d}^{{\varvec{jk}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{j + 1} } \\ {d_{j + 2} } \\ \vdots \\ \end{array} } \\ {d_{k} } \\ \end{array} } \right)$$

It is assumed that the changes of uncertain vectors $\varvec{a}^{{\varvec{j,k}}}$, $\varvec{c}^{{\varvec{jk}}}$ and $\varvec{h}^{{\varvec{tk}}}$ occur in the closed, convex and continuous regions U₁, U₂ and U₃, respectively. They are defined as:

$$U_{jk} \left( {q_{1} ,r_{1} } \right) = \left\{ {\varvec{a}^{{\varvec{jk}}} :\varvec{a}^{{\varvec{jk}}} =\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }} + \left( {{\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} } \right)\varvec{t}|\varvec{t} \in B_{{q_{1} }} \left( {r_{1} } \right)} \right\}$$

(6)

$$U_{jk}^{{\prime }} \left( {q_{2} ,r_{2} } \right) = \left\{ {\varvec{c}^{{\varvec{jk}}} :\varvec{c}^{{\varvec{jk}}} =\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }} + ({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )\varvec{u}|\varvec{u} \in B_{{q_{2} }}^{\prime } \left( {r_{2} } \right)} \right\}$$

(7)

$$U_{tk}^{{{\prime \prime }}} \left( {q_{3} ,r_{3} } \right) = \left\{ {\varvec{h}^{{\varvec{tk}}} :\varvec{h}^{{\varvec{tk}}} =\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }} + ({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )\varvec{v}|\varvec{v} \in B_{{q_{3} }}^{{{\prime \prime }}} \left( {r_{3} } \right)} \right\}$$

(8)

where

$$\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }} = \left. {\left( {\begin{array}{*{20}c} {\mu_{{a_{j + 1} }} } \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right)} \right\}\left( {k - j} \right){\text{times}}$$

$$\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }} = \left. {\left( {\begin{array}{*{20}c} {\mu_{{c_{j + 1} }} } \\ {\mu_{{c_{j + 1} }} } \\ \vdots \\ {\mu_{{c_{j + 1} }} } \\ \end{array} } \right)} \right\}\left( {k - j} \right){\text{times}}$$

$$\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }} = \left. {\left( {\begin{array}{*{20}c} {\mu_{{h_{t} }} } \\ {\mu_{{h_{t} }} } \\ \vdots \\ {\mu_{{h_{t} }} } \\ \end{array} } \right)} \right\}\left( {k - t} \right){\text{times}}$$

In Eqs. (6), (7) and (8), $\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }}$, $\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }}$ and $\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }}$ are the mean values of vectors $\varvec{a}^{{\varvec{jk}}}$, $\varvec{c}^{{\varvec{jk}}}$ and $\varvec{h}^{{\varvec{tk}}}$, respectively. $B_{{q_{1} }} \left( {r_{1} } \right)$, $B_{{q_{2} }} \left( {r_{2} } \right)$ and $B_{{q_{3} }} \left( {r_{3} } \right)$ are $l_{{q_{1} }}$, $l_{{q_{2} }}$ and $l_{{q_{3} }}$ norm bodies which are built by the following definitions, respectively:

$$B_{{q_{1} }} \left( {r_{1} } \right) = \{ \varvec{t}\epsilon {\text{R}}^{n} | \left\|\varvec{t}\right\|_{{q_{1} }} \le r_{1} \}$$

(9)

$$B_{{q_{2} }} \left( {r_{2} } \right) = \{ \varvec{u}\epsilon {\text{R}}^{n} | \left\|\varvec{u}\right\|_{{q_{2} }} \le r_{2} \}$$

(10)

$$B_{{q_{3} }} \left( {r_{3} } \right) = \{ \varvec{v}\epsilon {\text{R}}^{n} | \left\|\varvec{v}\right\|_{{q_{3} }} \le r_{3} \}$$

(11)

${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }}$, ${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }}$ and ${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }}$ are (k − j) × (k − j), (k − j) × (k − j) and (k − t) × (k − t) symmetric positive definite matrices, respectively. They are square root matrices of covariance matrices of uncertain vectors $\varvec{a}^{{\varvec{jk}}}$, $\varvec{c}^{{\varvec{jk}}}$ and $\varvec{h}^{{\varvec{tk}}}$, respectively (Johnson and Wichern 2007). They are calculated as:

$${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} = {\mathbf{C}}_{{\varvec{a}^{{\varvec{jk}}} }}^{{\frac{1}{2}}} \varvec{ }$$

(12)

$${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} = {\mathbf{C}}_{{\varvec{c}^{{\varvec{jk}}} }}^{{\frac{1}{2}}}$$

(13)

$${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} = {\mathbf{C}}_{{\varvec{h}^{{\varvec{tk}}} }}^{{\frac{1}{2}}} \varvec{ }$$

(14)

In Eqs. (12), (13) and (14), $\varvec{C}_{{\varvec{a}^{{\varvec{jk}}} }}$, $\varvec{C}_{{\varvec{c}^{{\varvec{jk}}} }}$ and $\varvec{C}_{{\varvec{h}^{{\varvec{tk}}} }}$ are the covariance matrices of uncertain vectors $\varvec{a}^{{\varvec{jk}}}$, $\varvec{c}^{{\varvec{jk}}}$ and $\varvec{h}^{{\varvec{tk}}}$, respectively. The covariance matrix is symmetric and positive definite (Johnson and Wichern 2007).

In practice, the uncertainty regions defined in (6), (7) and (8) describe the changes of stochastic vectors $\varvec{a}^{{\varvec{jk}}}$, $\varvec{c}^{{\varvec{jk}}}$ and $\varvec{h}^{{\varvec{tk}}}$ from their mean values, which are $\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }}$, $\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }}$ and $\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }}$, respectively. These changes are affected by the change in slope of ${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }}$, ${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }}$ and ${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }}$ matrices and are defined as the disorders occurring in $B_{{q_{1} }} \left( {r_{1} } \right)$, $B_{{q_{2} }} \left( {r_{2} } \right)$ and $B_{{q_{3} }} \left( {r_{3} } \right)$, respectively.

Applying the worst case in (5) (here, since m_jk is a cost, the worst case for m_jk means choosing the supremum of m_jk vector which can occur in $U_{1} \left( {q_{1} ,r_{1} } \right)$, $U_{2} \left( {q_{2} ,r_{2} } \right)$ and $U_{3} \left( {q_{3} ,r_{3} } \right)$), we have:

$$\begin{aligned} {\text{Robust}}\quad m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) & = \mathop { \sup }\limits_{{\begin{array}{*{20}c} {\varvec{a}^{{\varvec{jk}}} \epsilon U_{1} \left( {q_{1} ,r_{1} } \right), \varvec{c}^{{\varvec{jk}}} \epsilon U_{2} \left( {q_{2} ,r_{2} } \right) {\text{and}} } \\ {\varvec{h}^{{\varvec{tk}}} \epsilon U_{3} \left( {q_{3} ,r_{3} } \right)} \\ \end{array} }} m_{jk} \\ & = \mathop { \sup }\limits_{{\begin{array}{*{20}c} {\varvec{a}^{{\varvec{jk}}} \epsilon U_{1} \left( {q_{1} ,r_{1} } \right), \varvec{c}^{{\varvec{jk}}} \epsilon U_{2} \left( {q_{2} ,r_{2} } \right) {\text{and}} } \\ {\varvec{h}^{{\varvec{tk}}} \epsilon U_{3} \left( {q_{3} ,r_{3} } \right)} \\ \end{array} }} \left( {\left( {\varvec{a}^{{\varvec{jk}}} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + (\varvec{c}^{{\varvec{jk}}} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} + \mathop \sum \limits_{t = j + 1}^{k - 1} \left( {\left( {\varvec{h}^{{\varvec{tk}}} } \right)^{T} \varvec{d}^{{\varvec{tk}}} } \right)} \right) \\ & = \mathop { \sup }\limits_{{\varvec{a}^{{\varvec{jk}}} \epsilon U_{1} \left( {q_{1} ,r_{1} } \right)}} \left( {\left( {\varvec{a}^{{\varvec{jk}}} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right) + \mathop {\sup }\limits_{{\varvec{c}^{{\varvec{jk}}} \epsilon U_{2} \left( {q_{2} ,r_{2} } \right)}} \left( {\left( {\varvec{c}^{{\varvec{jk}}} } \right)^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right) \\ & \quad + \mathop {\sup }\limits_{{\varvec{h}^{{\varvec{tk}}} \epsilon U_{3} \left( {q_{3} ,r_{3} } \right)}} \left( {\mathop \sum \limits_{t = j + 1}^{k - 1} \left( {\varvec{h}^{{\varvec{tk}}} } \right)^{T} \varvec{d}^{{\varvec{tk}}} } \right) \\ \end{aligned}$$

(15)

Using definitions (6), (7) and (8) in relation (15), we have:

$$\begin{aligned} {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) & = \left( {\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + \mathop { \sup }\limits_{{\left\| \varvec{t} \right\|_{{q_{1} }} \le r_{1} }} \left( {\left( {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )\varvec{t}^{{\varvec{a}^{{\varvec{jk}}} }} } \right)^{T} \varvec{e}^{{\varvec{jk}}} } \right) + (\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} + \mathop { \sup }\limits_{{\left\| \varvec{u} \right\|_{{q_{2} }} \le r_{2} }} \left( {\left( {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )\varvec{u}^{{\varvec{c}^{{\varvec{jk}}} }} } \right)^{T} \varvec{d}^{{\varvec{jk}}} } \right) \\ & \quad + \mathop \sum \limits_{t = j + 1}^{k - 1} (\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} + \mathop \sum \limits_{t = j + 1}^{k - 1} \mathop { \sup }\limits_{{\left\| \varvec{v} \right\|_{{q_{3} }} \le r_{3} }} \left( {\left( {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )\varvec{v}^{{\varvec{h}^{{\varvec{tk}}} }} } \right)^{T} \varvec{d}^{{\varvec{tk}}} } \right) \\ & = \left( {\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + \mathop { \sup }\limits_{{\left\| \varvec{t} \right\|_{{q_{1} }} \le r_{1} }} \left( {\left( {\varvec{t}^{{\varvec{a}^{{\varvec{jk}}} }} } \right)^{\varvec{T}} ({\mathbf{W}}_{{\varvec{a}^{{\varvec{j} + 1}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right) + (\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} + \mathop { \sup }\limits_{{\left\| \varvec{u} \right\|_{{q_{2} }} \le r_{2} }} \left( {\left( {\varvec{u}^{{\varvec{c}^{{\varvec{jk}}} }} } \right)^{\varvec{T}} ({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right) \\ & \quad + \mathop \sum \limits_{t = j + 1}^{k - 1} (\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} \\ & \quad + \mathop \sum \limits_{t = j + 1}^{k} \mathop { \sup }\limits_{{\left\| \varvec{v} \right\|_{{q_{3} }} \le r_{3} }} \left( {\left( {\varvec{v}^{{\varvec{h}^{{\varvec{tk}}} }} } \right)^{\varvec{T}} ({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right) \\ \end{aligned}$$

(16)

Based on the definition of the dual norm, the dual of the $l_{{q_{1} }}$, $l_{{q_{2} }}$ and $l_{{q_{3} }}$ norms are the $l_{{p_{1} }}$, $l_{{p_{2} }}$ and $l_{{p_{3} }}$ norms, respectively, where q₁, q₂, q₃, p₁, p₂ and p₃ satisfy 1/p₁ + 1/q₁ = 1, 1/p₂ + 1/q₂ = 1 and 1/p₃ + 1/q₃ = 1. Hence, using the definition of the dual norm in (16), it is concluded that:

$$\begin{aligned} {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) & = \left( {\varvec{\mu}^{{\varvec{a}^{{\varvec{jk}}} }} } \right)^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + (\varvec{\mu}^{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} \\ & \quad + \mathop \sum \limits_{t = j + 1}^{k - 1} (\varvec{\mu}^{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} + \mathop \sum \limits_{t = j + 1}^{k} r_{3} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} ; 1/p_{1} + 1/q_{1} = 1; 1/p_{2} + 1/q_{2} \\ & = 1; 1/p_{3} + 1/q_{3} = 1 \\ \end{aligned}$$

(17)

A robust model is proposed in (17) which obtains robust amounts of m_jk by selecting various norm bodies and radiuses for U₁, U₂ and U₃ uncertainty regions (Hanafizadeh and Seifi 2006). Considering the definition of m_jk in (5), robust formulation can be summarized as follows:

$$\begin{aligned} {\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) & = m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} ;1/p_{1} \\ & \quad + 1/q_{1} = 1; 1/p_{2} + 1/q_{2} = 1; 1/p_{3} + 1/q_{3} = 1 \\ \end{aligned}$$

(18)

m_jk is the cost incurred in periods j + 1 through k calculated by the Wagner–Whitin algorithm without considering robustness.

And relation (2) for the robust case can be written as:

$${\text{Robust}}\; f_{k} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) = \mathop {\hbox{min} }\limits_{0 \le j < k} \left[ {{\text{Robust }}f_{j} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) + {\text{Robust }} m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)} \right]$$

(19)

Relations (18) and (19) are the final definitions of the robust cost of production planning within the Wagner–Whitin algorithm.

Analysis of the Wagner–Whitin algorithm with robust costs

Based on what is defined in (18), $r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$, $r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ and $r_{3} \sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ are added to m_jk to calculate ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$. The amplitude of $r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$, $r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ and $r_{3} \sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ is dependent on the form and chosen radius of uncertainty regions r₁, r₂ and r₃ and the size of ${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }}$, ${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }}$ and ${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }}$ matrices. r₁, r₂, and r₃ are the radiuses of uncertainty regions and are positive real numbers. Moreover, based on the norm function properties (Boyd and Vandenberghe 2004), $\left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$, $\left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ and $\sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ are always nonnegative real numbers. Therefore, ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ is always greater than m_jk. Another important element in the difference between ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ and m_jk is selecting the q₁, q₂ and q₃ norms. The effects of these norms are summarized in the following observation.

Observation 1

Regarding relation (19), if $q_{i} \left( {i = 1,2,3} \right)$ in ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ increases, then the uncertainty region increases, too. As far as the dual norm definition is concerned (Boyd and Vandenberghe 2004), the greater $q_{i} \left( {i = 1,2,3} \right)$ gets us into a smaller $p_{i} \left( {i = 1,2,3} \right)$ and based on relation (1), if $p_{i} \left( {i = 1,2,3} \right)$ gets smaller, $l_{{p_{i} }} \left( {i = 1,2,3} \right)$ norm gets greater. To explain it more clearly, it results in a bigger uncertainty region:

$$\begin{aligned} U_{jk} \left( {\infty ,r_{1} } \right) & > U_{jk} \left( {2,r_{1} } \right) > U_{jk} \left( {1,r_{1} } \right), \\ U_{jk}^{{\prime }} \left( {\infty ,r_{2} } \right) & > U_{jk}^{{\prime }} \left( {2,r_{2} } \right) > U_{jk}^{{\prime }} \left( {1,r_{2} } \right), \\ U_{tk}^{{{\prime \prime }}} \left( {\infty ,r_{3} } \right) & > U_{tk}^{{{\prime \prime }}} \left( {2,r_{3} } \right) > U_{tk}^{{{\prime \prime }}} \left( {1,r_{3} } \right). \\ \end{aligned}$$

Proposition 1

A greater uncertainty region, for either $U_{jk} \left( {q_{1} ,r_{1} } \right)$ or $U_{jk}^{{\prime }} \left( {q_{2} ,r_{2} } \right)$ or $U_{tk}^{{{\prime \prime }}} \left( {q_{3} ,r_{3} } \right)$, makes a greater ${\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right):$

$${\text{Robust}} \;m_{jk} \left( {1, q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \le {\text{Robust}} \;m_{jk} \left( {2, q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \le {\text{Robust}} \;m_{jk} \left( {\infty , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$$

(20)

$${\text{Robust}} \;m_{jk} \left( {q_{1} , 1,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \le {\text{Robust}} \;m_{jk} \left( {q_{1} , 2,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \le {\text{Robust}} \;m_{jk} \left( {q_{1} , \infty ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$$

(21)

$${\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,1, r_{1} , r_{2} ,r_{3} } \right) \le {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,2, r_{1} , r_{2} ,r_{3} } \right) \le {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,\infty , r_{1} , r_{2} ,r_{3} } \right)$$

(22)

Proof of relation (20)

From (1), we have:

$$\left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{1} \ge \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{2} \ge \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{\infty }$$

(23)

If all sides of the above relation are multiplied by r₁, which is a positive real number, we have:

$$r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{1} \ge r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{2} \ge r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{\infty }$$

(24)

By adding $m_{jk} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }}$ to all sides of the above relation, we get the following relation:

$$\begin{aligned} m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{1} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \hfill \\ \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{2} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \hfill \\ \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{\infty } + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \hfill \\ \end{aligned}$$

(25)

Based on the relation 1/p₁ + 1/q₁ = 1, we have the following results:

$${\text{If}} \quad q_{1} = 1\quad {\text{then}}\quad p_{1} = \infty$$

(26)

$${\text{If}}\quad q_{1} = 2 \quad {\text{then}}\quad p_{1} = 2$$

(27)

$${\text{If}}\quad q_{1} = \infty \quad {\text{then}}\quad p_{1} = 1$$

(28)

According to relations (18), (25), (26), (27) and (28), we have:

$${\text{Robust}} \;m_{jk} \left( {\infty , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {2, q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {1, q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$$

(29)

. □

Proof of relation (20)

From (1), we have:

$$\left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{1} \ge \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{2} \ge \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{\infty }$$

(30)

If all sides of the above relation are multiplied by the positive real number r₂, we have:

$$r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{1} \ge r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{2} \ge r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{\infty }$$

(31)

We add $m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{3} \sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ to all sides of the above relation. We have:

$$\begin{aligned} & m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{1} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ & \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{2} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ & \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{\infty } + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ \end{aligned}$$

(32)

Based on the relation 1/p₂ + 1/q₂ = 1, we have the following results:

$${\text{If}}\quad q_{2} = 1\quad {\text{then}}\quad p_{2} = \infty$$

(33)

$${\text{If}} \quad q_{2} = 2 \quad {\text{then}}\quad p_{2} = 2$$

(34)

$${\text{If}} \quad q_{2} = \infty \quad {\text{then}}\quad p_{2} = 1$$

(35)

According to relations (15), (32), (33), (34) and (35), we have:

$${\text{Robust}} \;m_{jk} \left( {q_{1} , \infty ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {q_{1} , 2,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {q_{1} , 1,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$$

(36)

. □

Proof of relation (21)

From (1), we have:

$$\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{1} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{2} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{\infty } \quad {\text{for}}\quad \forall \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|\varvec{ }\left( {t = j + 1, j + 2, \ldots , k} \right),$$

which means:

$$\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{j + }{\mathbf{1}}\varvec{,k}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{j + }{\mathbf{1}}\varvec{,k}}} } \right\|_{1} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{j + }{\mathbf{1}}\varvec{,k}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{j} + {\mathbf{1}},\varvec{k}}} } \right\|_{2} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{j} + {\mathbf{1}},\varvec{k}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{j} + {\mathbf{1}},\varvec{k}}} } \right\|_{\infty }$$

(37)

$$\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{j} + {\mathbf{2}},\varvec{k}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{j} + {\mathbf{2}},\varvec{k}}} } \right\|_{1} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{j} + {\mathbf{2}},\varvec{k}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{j} + {\mathbf{2}},\varvec{k}}} } \right\|_{2} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{j} + {\mathbf{2}},\varvec{k}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{j} + {\mathbf{2}},\varvec{k}}} } \right\|_{\infty }$$

(38)

$$\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{kk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{kk}}} } \right\|_{1} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{kk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{kk}}} } \right\|_{2} \ge \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{kk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{kk}}} } \right\|_{\infty }$$

(39)

We add relations (37), (38) and (39) to each other to get:

$$\mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{1} \ge \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{2} \ge \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{\infty }$$

(40)

We multiply all sides of the above relation by the positive real number r₃. Thus, we have:

$$r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{1} \ge r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{2} \ge r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{\infty }$$

(41)

We add $m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ to all sides of relation (41), and we then get:

$$\begin{aligned} & m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{1} \\ & \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{2} \\ & \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{\infty } \\ \end{aligned}$$

(42)

Based on the relation 1/p₃ + 1/q₃ = 1, we have the following results:

$${\text{If}} \quad q_{3} = 1 \quad {\text{then}}\quad p_{3} = \infty$$

(43)

$${\text{If}}\quad q_{3} = 2\quad {\text{then}}\quad p_{3} = 2$$

(44)

$${\text{If}}\quad q_{3} = \infty \quad {\text{then}}\quad p_{3} = 1$$

(45)

According to relations (18), (42), (43), (44) and (45), we have:

$${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,\infty , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,2, r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,1, r_{1} , r_{2} ,r_{3} } \right) .$$

(46)

□

The radius of uncertainty regions $\left( {r_{i} i = 1,2,3} \right)$ is an important element in robust formulation (18) which is the difference between ${\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ and m_jk. Since r_i (for i = 1, 2, 3) is a positive real number, based on (18) the existence of the following observation seems important.

Observation 2

When the radius of any uncertainty regions (either r₁ or r₂ or r₃) increases, the amount of ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ increases, too.

Proof for the uncertainty region $\varvec{r}_{1}$

Imagine

$$r_{1} \ge r_{1}^{{\prime }}$$

Then, by multiplying the positive real number $\left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$ to both sides of the above relation, we have:

$$r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} \ge r_{1}^{{\prime }} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$$

(47)

Now we add the positive real number $m_{jk} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ to both sides of relation (47) and we get the following relation:

$$\begin{aligned} & m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ & \ge m_{jk} + r_{1}^{{\prime }} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ \end{aligned}$$

(48)

Regarding relation (18) and the above relation, it can be seen that when r₁ ≥ r^′₁ we have:

$${\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1}^{'} , r_{2} ,r_{3} } \right)$$

. □

Proof for the uncertainty region $\varvec{r}_{2}$

Imagine

$$r_{2} \ge r_{2}^{{\prime }}$$

Then, by multiplying the positive real number $\left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ to both sides of the above relation, we have:

$$r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} \ge r_{2}^{{\prime }} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$$

(49)

Now we add the positive real number $m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{3} \sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ to both sides of relation (49) and we get the following relation:

$$\begin{aligned} & m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ & \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2}^{{\prime }} ({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}}_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ \end{aligned}$$

(50)

Regarding relation (18) and the above relation (50), it can be seen that when r₂ ≥ r^′₂, we have:

$${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2}^{'} ,r_{3} } \right).$$

□

Proof for the uncertainty region $\varvec{r}_{3}$

Imagine

$$r_{3} \ge r_{3}^{{\prime }}$$

Then, by multiplying the positive real number $\sum\nolimits_{t = j + 1}^{k} {\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} }$ to both sides of the above relation, we have:

$$r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \ge r_{3}^{{\prime }} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }}$$

(51)

Now we add the positive real number $m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ to both sides of relation (51) and we get the following relation:

$$\begin{aligned} & m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ & \ge m_{jk} + r_{1} \left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }} + r_{2} \left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }} + r_{3}^{{\prime }} \mathop \sum \limits_{t = j + 1}^{k} \left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }} \\ \end{aligned}$$

(52)

Regarding relation (18) and the above relation, it can be seen that when r₃ ≥ r^′₃, we have:

$${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) \ge {\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3}^{'} } \right).$$

□

The variance from the mean value and the covariance of $\varvec{a}^{{\varvec{jk}}}$, $\varvec{c}^{{\varvec{jk}}}$ or $\varvec{h}^{{\varvec{tk}}}$ is also another element in the difference between ${\text{Robust}} m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ and m_jk. This difference is in ${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }}$, ${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }}$ or ${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }}$ which are the square matrix of the covariance matrix of uncertain parameters $\varvec{a}^{{\varvec{jk}}}$, $\varvec{c}^{{\varvec{jk}}}$ and $\varvec{h}^{{\varvec{tk}}}$, respectively. Generally speaking, when there are two matrices ${\mathbf{W}}$ and ${\mathbf{W^{\prime}}}$ while ${\mathbf{W^{\prime}}} \le {\mathbf{W}}$, it means that each and every element of ${\mathbf{W}}$ is greater than or equal to the corresponding element of ${\mathbf{W^{\prime}}}$. The forthcoming observation explains the influence of the covariance matrix on the calculated ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$.

Observation 3

A greater covariance matrix results in a bigger ${\text{Robust}} \;m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$.

For calculating relation (18), we need to calculate $\left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$, $\left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ and $\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }}$. For calculating these three norms, each of the rows of ${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }}$, ${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }}$ and ${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }}$, the square matrices of the covariance matrices, is multiplied by the vectors $\varvec{e}^{{\varvec{jk}}}$, $\varvec{d}^{{\varvec{jk}}}$ and $\varvec{d}^{{\varvec{tk}}}$, respectively. After that, the p₁ norm of $({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}}$, the p₂ norm of $({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}}$ and the p₃ norm of $({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}}$ are calculated and added to each other. Since norm is a nonnegative real number (Boyd and Vandenberghe, 2004), the sum of these three norms is of course a nonnegative real number. Therefore, the bigger the components of ${\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }}$, ${\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }}$ and ${\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }}$, the bigger $\left\| {({\mathbf{W}}_{{\varvec{a}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{e}^{{\varvec{jk}}} } \right\|_{{p_{1} }}$, $\left\| {({\mathbf{W}}_{{\varvec{c}^{{\varvec{jk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{jk}}} } \right\|_{{p_{2} }}$ and $\left\| {({\mathbf{W}}_{{\varvec{h}^{{\varvec{tk}}} }} )^{\varvec{T}} \varvec{d}^{{\varvec{tk}}} } \right\|_{{p_{3} }}$ become, respectively, and based on (18), a greater $Robust m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ is achieved.

Application of the Wagner–Whitin algorithm with robust costs

In this part, one example from the literature is studied and solved with the classical Wagner–Whitin algorithm and with the robust algorithm presented in this paper. The coming example is taken from (Johnson and Montgomery 1974).

This example is a single-item production planning problem and has 6-month planning horizon. The manager can purchase the product at the beginning of each month. The details are depicted in Table 1. Moreover, neither initial inventory is assumed nor shortages are planned. The problem is to determine the quantities to be procured at the beginning of each month.

Table 1 Data for the example

In this problem, there are three different costs. The first one is the fixed cost of each period which we should pay if procurement is made at the beginning of each period. This fixed cost of each period is different for different periods (months) but here we assume that they are also correlated with each other and the covariance matrix is given in Table 2.

Table 2 Covariance matrix of the fixed costs for the example

In addition to the fixed costs, there are variable unit costs and unit inventory costs for each month. The first one is related to the cost of producing or purchasing each unit in each month, and the latter one is for the cost of keeping a unit of product in the warehouse from a period to the next period. In this problem, it is assumed that variable unit costs are correlated with each other and the covariance matrix is given in Table 3.

Table 3 Covariance matrix of the cost of producing each unit in each period for the example

Moreover, assuming correlation between unit inventory costs, the covariance matrix is given in Table 4 for this example.

Table 4 Covariance matrix of the unit inventory costs for the example

Firstly, we consider a one-period horizon. For this, we have: b₁ = d₁ = 60, and f₁ = f₀ + m₀₁ = f₀ + a₁ + c₁b₁ = 0 + 150 + 7(60) = 570. Hence, by having j = 0 and k = 1, we have:

$$m_{01} = 570,$$

$$f_{0} = 0,$$

$$f_{1} = 570,$$

Imagine q₁ = 3, q₂ = 2, q₃ = 5, r₁ = 2, r₂ = 1.1 and r₃ = 1.2.

$$\begin{aligned} {\text{Robust}}\; m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) & = {\text{Robust}}\; m_{01} \left( {3, 2, 5, 2, 1.1, 1.2} \right) \\ & = m_{01} + 2\left\| {({\mathbf{W}}_{{\varvec{a}^{01} }} )^{\varvec{T}} \varvec{e}^{{{\mathbf{01}}}} } \right\|_{1.5} + 1.1\left\| {({\mathbf{W}}_{{\varvec{c}^{01} }} )^{\varvec{T}} \varvec{d}^{{{\mathbf{01}}}} } \right\|_{2} = 680.130191 \\ \end{aligned}$$

$${\text{Robust}} \;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 0$$

$${\text{Robust}}\; f_{1} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = {\text{Robust}} \;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}}\; m_{01} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 680.130191$$

Now, we consider the first two periods (months). Last production can occur either in period 1 or in period 2. We need to evaluate both cases:

$$\begin{aligned} {\text{Robust}} \;f_{2} \left( {3, 2, 5, 2, 1.1, 1.2} \right) & = \mathop {\hbox{min} }\limits_{0 \le j < 2} \left[ {{\text{Robust}} \;f_{j} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{j2} \left( {3, 2, 5, 2, 1.1, 1.2} \right)} \right] \\ & = { \hbox{min} }\left\{ {\begin{array}{*{20}c} {{\text{Robust}} \;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{02} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 1736.457322} \\ {{\text{Robust}}\; f_{1} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{12} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 1612.902594} \\ \end{array} } \right\} \\ & = 1612.902594 \\ \end{aligned}$$

As we can see, for a two-period horizon, the optimal last point of zero inventory is at the end of period 1 (j^*₂ = 1) and thus the optimal period for the last procurement is period 2.

For a three-period horizon, we have:

$$\begin{aligned} {\text{Robust}} \;f_{3} \left( {3, 2, 5, 2, 1.1, 1.2} \right) & = \mathop {\hbox{min} }\limits_{0 \le j < 3} \left[ {{\text{Robust}}\; f_{j} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{j3} \left( {3, 2, 5, 2, 1.1, 1.2} \right)} \right] \\ & = { \hbox{min} }\left\{ {\begin{array}{*{20}c} {{\text{Robust}} \;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{03} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 3828.5132} \\ {{\text{Robust}} \;f_{1} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{13} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 3123.89178} \\ {{\text{Robust }}\;f_{2} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}}\; m_{23} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 2869.142577} \\ \end{array} } \right\} \\ & = 2869.142577 \\ \end{aligned}$$

The optimal period of last procurement is 3 and j^*₃ = 2.

For a four-period horizon:

$$\begin{aligned} {\text{Robust}} \;f_{4} \left( {3, 2, 5, 2, 1.1, 1.2} \right) & = \mathop {\hbox{min} }\limits_{0 \le j < 4} \left[ {{\text{Robust}} \;f_{j} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{j4} \left( {3, 2, 5, 2, 1.1, 1.2} \right)} \right] \\ & = \hbox{min} \left\{ \begin{aligned} {\text{Robust}} \;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{04} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 7129.702305 \hfill \\ {\text{Robust}} \;f_{1} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{14} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 5905.622864 \hfill \\ {\text{Robust}} \;f_{2} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{24} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 5344.611239 \hfill \\ {\text{Robust}} \;f_{3} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{34} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 4448.729854 \hfill \\ \end{aligned} \right\} \\ & = 4448.729854 \\ \end{aligned}$$

It can be seen that j^*₄ = 3.

For a five-period horizon:

$$\begin{aligned} {\text{Robust}} \;f_{5} \left( {3, 2, 5, 2, 1.1, 1.2} \right) & = \mathop {\hbox{min} }\limits_{0 \le j < 5} \left[ {{\text{Robust}}\; f_{j} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{j5} \left( {3, 2, 5, 2, 1.1, 1.2} \right)} \right] \\ & = \hbox{min} \left\{ \begin{aligned} {\text{Robust }}\;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust }} \;m_{05} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 9995.161173 \hfill \\ {\text{Robust }} \;f_{1} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust }} \;m_{15} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 8304.894676 \hfill \\ {\text{Robust}} \;f_{2} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}}\; m_{25} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 7478.44898 \hfill \\ {\text{Robust}} \;f_{3} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{35} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 5841.925805 \hfill \\ {\text{Robust}} \;f_{4} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{45} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 5220.798195 \hfill \\ \end{aligned} \right\} \\ & = 5220.798195 \\ \end{aligned}$$

For which j^*₅ = 4.

For a six-period horizon:

$$\begin{aligned} {\text{Robust}} \;f_{6} \left( {3, 2, 5, 2, 1.1, 1.2} \right) & = \mathop {\hbox{min} }\limits_{0 \le j < 6} \left[ {{\text{Robust}} \;f_{j} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{j6} \left( {3, 2, 5, 2, 1.1, 1.2} \right)} \right] \\ & = \hbox{min} \left\{ \begin{aligned} {\text{Robust}} \;f_{0} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{06} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 12489.63045 \hfill \\ {\text{Robust }} \;f_{1} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust }} \;m_{16} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 10400.56671 \hfill \\ {\text{Robust}}\; f_{2} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{26} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 9270.98068 \hfill \\ {\text{Robust}} \;f_{3} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{36} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 7143.347851 \hfill \\ {\text{Robust}} \;f_{4} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{46} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 6071.781954 \hfill \\ {\text{Robust}} \;f_{5} \left( {3, 2, 5, 2, 1.1, 1.2} \right) + {\text{Robust}} \;m_{56} \left( {3, 2, 5, 2, 1.1, 1.2} \right) = 6073.844243 \hfill \\ \end{aligned} \right\} \\ & = 6071.781954 \\ \end{aligned}$$

For which j^*₆ = 4.

The results of the robust approach are summarized in Table 5.

Table 5 Values of ${\text{Robust}} f_{j} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right) + {\text{Robust}} m_{jk} \left( {q_{1} , q_{2} ,q_{3} , r_{1} , r_{2} ,r_{3} } \right)$ for the example with robust costs

As it can be seen in the above table, the minimum cost over the six-period planning horizon is ${\text{Robust}} f_{6} = 6071.781954$, and since j^*₆ = 4, we order in period 5 an amount equal to b^*₅ = d₅ + d₆ = 200 and therefore b^*₆ = 0. Since j^*₆ = 4, at the end of period 4 the warehouse is empty. Therefore, we next consider a four-period horizon. For a four-period horizon, we saw that j^*₄ = 3 and thus at the end of period 3 the warehouse becomes empty. Therefore, b^*₄ = 200. Now consider a three-period horizon: j^*₃ = 2, and thus we order at period 3 an amount of b^*₃ = 140. For a two-period horizon, we have j^*₂ = 1 and therefore we need to make an order at the beginning of period 2, an amount equal to b^*₂ = d₂ = 100. Then, we note the first horizon and we have j^*₁ = 0. Thus, at the beginning of the first period, we order b^*₁ = d₁ = 60. Therefore, the robust optimal plan is to order lots of 60, 100, 140, 200, 200 and 0 over the six-period horizon as illustrated in Table 6.

Table 6 Robust optimal plan for the example

The results of the classical Wagner–Whitin algorithm as indicated in Johnson and Montgomery (1974) are summarized in Table 7.

Table 7 Values of $f_{j} + m_{jk}$ for the example with dynamic demands

From Table 7, you can see that f₆ = 5620 and j^*₆ = 4. Therefore, we order in period 5 an amount of b^*₅ = d₅ + d₆ = 200 and b^*₆ = 0. Since j^*₆ = 4, the warehouse is empty at the end of period 4. Thus, we consider a four-period horizon. In the table, we see that for a four-period horizon, j^*₄ = 3, and therefore at the end of period 3, the ware house is empty. Hence, b^*₄ = 200, and then we consider a three-period horizon for which j^*₃ = 1 and we order at period 2 an amount equal to b^*₂ = d₂ + d₃ = 240. Therefore, b^*₃ = 0. Since j^*₃ = 1, we next consider the first horizon: j^*₁ = 0 and at the beginning of the first period we order b^*₁ = d₁ = 60. Finally, the classical optimal plan is to order lots of 60, 240, 0, 200, 200 and 0 over the six-period horizon. You can find this plan in Table 8.

Table 8 Classical optimal plan for the example

Conclusion

In this paper, an important, real-world extension of the stochastic Wagner–Whitin algorithm is dealt with, in the case where costs are non-stationary and correlated. Since the robust approach takes the information about the variance and correlation of historical data into account, it is expected to be more reliable than using only the mean of uncertain cost. One of the main aspects and features of this research is that we try to solve one of the most famous classic inventory problems with a proactive approach: considering uncertain costs and solving robust counterpart of the lot-sizing problem with the Wagner–Whitin algorithm. Consider a company using the Wagner–Whitin algorithm for finding out the amount and frequency of orders in a production planning system. In this system, if the costs of each period are known at the beginning of the planning horizon, by using the Wagner–Whitin algorithm we can easily calculate and find out that the orders that should be made at the beginning of each period and the amount of these orders. We confront the problem when the costs vary around its mean with some variations measured by its variance and correlated with each other, and the decision maker does not know about the exact costs at the beginning of the planning horizon. In this case, the optimum solution of the Wagner–Whitin algorithm is not necessarily practical. We used a robust approach to deal with the uncertain costs. In the presented approach, the variations of the uncertain costs are assumed to be in a convex and closed set. This set is the uncertainty region, and its size and shape are formed based on the information of the covariance matrix. According to what is defined in relation (18), a positive term is added to the cost of production planning within the robust Wagner–Whitin algorithm due to uncertainty in costs. If a decision maker predicts that the future circumstances are more risky, they would decide to be more conservative. Thus, for the variations of uncertain costs, they would consider a bigger uncertainty region and as the uncertainty region gets bigger, the cost of production planning within the robust Wagner–Whitin algorithm increases, too.

As future studies, it is proposed to researchers to compare the robust method with the classical Wagner–Whitin algorithm with a level of buffer and perform simulation on the results of such a comparison. Comparing the robust method with other methods from the literature is not appropriate while different types of information such as pdf in case of probabilistic cost or fuzzy information in case of possibilistic costs are used. However, in our proposed method, the only information is covariance and mean of uncertain costs.

The idea of robust approach when costs are correlated and non-stationary is quite novel and intact in the area of supply chain. This paper, as the first one in this area, can be leading to more research for the cases when different parameters of supply chain models are uncertain and correlated with each other. More precisely, a similar research to this study can be extended particularly if the demands of a lot-sizing problem are uncertain and correlated with each other. Moreover, one can study the case when lead times are not zero and are correlated with each other while demands are uncertain as well. The proposed method is solved for only one single problem, and the optimal robust solution for this problem is obtained. It is conspicuous that for generalizing the better quality of the robust solution, it is required to conduct a general simulation for a group of problems in large numbers and then the judgment of the quality of robust solution is comparable to the classical one. In addition, since the presented method is for the single-item production, the method can be extended to the multi-item production case as well.

Since by applying the robust approach to relationships (2), (3) and (4), the Wagner–Whitin solution algorithm is still usable to solve lot-size robust model, its computational complexity follows the original algorithm.