A hybrid DEA-based K-means and invasive weed optimization for facility location problem

Abstract

In this paper, instead of the classical approach to the multi-criteria location selection problem, a new approach was presented based on selecting a portfolio of locations. First, the indices affecting the selection of maintenance stations were collected. The K-means model was used for clustering the maintenance stations. The optimal number of clusters was calculated through the Silhouette index. The efficiency of each cluster of stations was determined using the Charnes, Cooper and Rhodes input-oriented data envelopment analysis model. A bi-objective zero one programming model was used to select a Pareto optimal combination of rank and distance of stations. The Pareto solutions for the presented bi-objective model were determined using the invasive weed optimization method. Although the proposed methodology is meant for the selection of repair and maintenance stations in an oil refinery Company, it can be used in multi-criteria decision-making problems.

Introduction

Decision making is one of the main differences between human and other beings. Decision making and decision analysis has become an integral part of management science, and its formation history goes back to a distant past in human history. In many real-world problems, decision-maker is faced with numerous and various criteria rather than an objective or criteria and must act logically and systematically (Farahani et al. 2010). The philosophical basis of development of decision models is not limited to selecting or not selecting. Quantitative and qualitative criteria in a certain, uncertain or fuzzy space may be considered in decisions making based on mathematical models. These decision models are known as multiple-criteria decision-making (Tzeng and Huang 2011). Location selection problem is essentially a multi-criteria decision model. Different quantitative and qualitative criteria may be involved in the selection process. This is considered the most important strategic step in the process of manufacturing organizations. This decision is an irrevocable decision (Rao 2007). In many location problems, a series of obstacles in the new location need to be addressed. Obstacles often lead to not selecting the new location (Shiripour et al. 2012). Facility layout design affects the overall performance of production system, and thus, it is always considered a key factor for productivity improvement. Location problems for multi-criteria selection address quantitative and qualitative indices simultaneously (Yang et al. 2013). Given the importance of the strategic decision of location selection in the production process of industrial organizations, the present paper provides a new approach for multiple-criteria location selection. According to the presented methodology, a set of locations is selected rather than a single location. This methodology was employed because of the necessity for the combined selection of maintenance and repair places suitable for maintenance and repair activities of each station. Therefore, the aim of this case is to select an optimal Pareto combination from the designated locations to do maintenance and repair activities. The candidate location is placed in a number of clusters through K-means clustering algorithm. The efficiencies of the candidate locations in each cluster are determined through the data envelopment analysis model. Pareto analysis of rank and distance was conducted using a zero–one programming model based of invasive weed optimization algorithm.

The paper continues as follows: The second section presents the literature review. The third section describes the K-means algorithm. DEA model is presented in section four. Section five discusses the invasive weed optimization method. In the sixth section, a new framework for multi-objective location selection is presented. The seventh and eighth sections include a case study and conclusions, respectively.

Literature review

Nanthavanij and Asadathorn (1999) presented an analytical model for determination of dominant location. In their problem, cost contour reaches its minimum at the dominant location factor. The cost–noise successive minimization and goal programming techniques were used. The main variables for the vehicles location included cost coefficients and the noise level (Nanthavanij and Asadathorn 1999). Badri (1999) used the combined model of the analytic hierarchy process and multi-objective goal programming for the location problem. The main variables in their research include the following: Political situation of foreign country, Global competition and survival, Government regulations, Economics-related factors (Badri 1999). Arostegui et al. (2006) investigated the meta-heuristic algorithms of Tabu search, genetic algorithms and simulated annealing in solving facility location problems. They found that in most cases, and according to various criteria of optimality, Tabu search was more efficient (Arostegui et al. 2006). Dupont (2008) presented a zero–one programming model based on branch and bound algorithm to select a set of facilities, such as warehouses, plants, public facilities and antennas. The objective function aimed at minimizing the costs of investment and production and distribution (Dupont 2008). Thanh et al. (2008) presented a mixed integer linear program model for the location problem of production–distribution systems. Their model was dynamic (Thanh et al. 2008). Lin (2009) presented a stochastic model for the facility location problem. In their case, service level requirements were modeled through chance constrained programming (Lin 2009). Aydin and Murat (2013) presented a new hybrid model based on swarm intelligence for the facility location problem. In their view, two meta-heuristic models of particle swarm optimization and sample average approximation were combined in a location problem. Their results showed that with increasing dimensions of the problem, the designed model achieved a solution more efficiently (Aydin and Murat 2013). Nezhad et al. (2013) examined the single-source multi-product production/distribution facility location problem in the optimal location problems context. Their main approach was Lagrangian-based heuristics. They tested the designed model in larger dimensions. Results showed that the designed model had an acceptable efficiency in larger dimensions (Nezhad et al. 2013). Kia et al. (2013) proposed a mixed integer nonlinear programming model in a cellular manufacturing system in a dynamic environment for the layout problem. This model can determine the optimal value of production on each path (Kia et al. 2013). Khalili-Damghani et al. (2014) presented a mathematical model to design the layout process. The three main goals of the problem, investigated using the genetic algorithm, were the maximization of profit on each product, minimization of materials kept in warehouses and minimization of layout costs. According to the research results, the use of the genetic algorithm was more efficient in the larger dimensions of the problem in comparison with the simulated annealing algorithm and scatter search (Khalili-Damghani et al. 2014). Javadi and Shahrabi (2014) investigated the facility location problem based on the concept of clustering. In their approach, geographical barriers were taken into account for optimal urban deployment. They also used three DIJKSTRA distances, the shortest path algorithm and the Bug1 and Bug2 algorithms in robot moves to calculate the distances between demand point and facilities. Then, they evaluated distance functions based on demand point allocation, costs of logistics and response time (Javadi and Shahrabi 2014). Khalili-Damghani and Naderi (2014) studied the establishment–routing problem with regard to the logistics and support provided for soldiers in urban wars. The goal was to minimize the costs of repair and support centers which were analyzed by using a mathematical integer linear programming model (Khalili-Damghani and Naderi 2014). Shafigh et al. (2015) proposed a mathematical model to integrate layout configuration and production planning into the designs of distributed layouts. This problem includes manufacturing criteria and cost elements. The concept of resource elements (REs) was used in routing the processed components for modeling. The main idea of this research was based on balancing the workload in different sections (Shafigh et al. 2015). Regarding an establishment–routing problem for perishable goods, Khalili-Damghani et al. (2015) paid attention to two main goals, i.e., the minimization of the entire supply chain cost and the establishment of equilibrium in the workload of distribution centers. The analysis tool was NSGA-II (non-dominated sorting genetic algorithm). The research results were compared with exacts those of multi-objective methods (Khalili-Damghani et al. 2015). Sadjadi et al. (2016) proposed a mathematical model to solve the location design problem with respect to budget constraints on inelastic demands and customer patronizing behavior. This model was developed by the firefly algorithm (Sadjadi et al. 2016). Rabbani et al. (2016) employed a mathematical modeling approach to study social and economic objectives in a location problem and a routing problem simultaneously. They used the non-dominated sorting genetic algorithm to solve the model. The research results were compared with classic decomposition methods (Rabbani et al. 2016). Tahmasebi et al. (2017) introduced a model for the establishment–routing problem at post offices. The structure of the problem is bi-objective. The goal is to select certain locations from potential locations and select an optimal number of vehicles on routes. Goal programming was the tool used to determine the establishment locations of post offices in the 21 districts of Tehran. The goal was also to minimize the total system cost and time considered by researchers (Tahmasebi et al. 2017).

K-means algorithm

Clustering provides a way to find structure of complex data. Clustering is the process of grouping similar records in a cluster and non-similar records in different clusters (Rahman and Islam 2014). Similarity scale depends on the application of the problem (Adhau et al. 2014). Clustering quality depends on the similarity scale. It is through this that the hidden patterns are discovered, and new previously nonexistent knowledge is obtained (Velmurugan 2014). Clustering has applications in various areas such as machine learning, image processing, data mining, pattern recognition, bioinformatics, construction management, marketing, clustering document, intrusion detection, healthcare and information retrieval (Krishnasamy et al. 2014). The two clustering algorithms K-means and Fuzzy C-means are commonly used due to their ease of use. For n feature vectors, $\varvec{x}_{1} , \, \varvec{x}_{2} , \ldots ,\varvec{x}_{n}$, that fall into k clusters (k < n) the objective/cost function to be minimized is given as:

$$ J = \sum\limits_{j = 1}^{k} {\sum\limits_{i = 1}^{n} {\left| {\left| {x_{i}^{\left( j \right)} - c_{j} } \right|} \right|^{2} } } $$

(1)

m_i is the mean of vectors in cluster i and the term inside the summation is a chosen distance measure between data point $x_{i}^{\left( j \right)}$ and cluster c_j. The steps of K-means algorithm are as follows (Gurudath and Riley 2014):

• Step 1: Start,

• Step 2: Initialize $m_{1} ,m_{2} , \ldots ,m_{k}$,

• Step 3: While no change in mean,

• Step 4: Classify samples into clusters using estimated means,

• Step 5: For i running from 1 to k,

• Step 6: Calculate the distance between each feature and the initialize cluster mean,

• Step 7: If the criterion in Eq. 7 is satisfied proceed to Step 9 else go to Step 8,

• Step 8: Replace m_i with mean of all samples for cluster i,

• Step 9: End for,

• Step 10: End while,

• Step 11: Stop.

The main idea of the K-means algorithm presented above is to define K centers for each cluster. These centers must be selected carefully, because different centers yield different results. Therefore, the best selection is to put the centers as distant as possible from each other. The next step is to assign each pattern to the closest center. When all the points are assigned to existing centers, the first step is completed, and a preliminary grouping is done. Then, K new center must be calculated for the clusters in the previous step. After determining the new K centers, the data are assigned to appropriate centers. This process is repeated until the K centers do not vary. The algorithm aims at minimizing an objective function which is the squared error.

Data envelopment analysis (DEA)

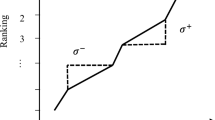
DEA was introduced by Charnes et al. (1978). This model was developed by Banker et al. (1984). A DEA does not require a priori weights on inputs and outputs (Lee and Saen 2012). In DEA, decision making is evaluated through different inputs and outputs (Amirteimoori and Kordrostami 2012). DEA models are classified into the input-oriented and output-oriented. Input-oriented models use less input to yield the same outputs, and output-oriented models use less outputs to yield the same inputs. In another classification, DEA models are classified into multiplier models and data envelopment models. Secondary data envelopment models are of multiplier models (Charles et al. 2012). In DEA, the ratio of the sum of weighted outputs to the sum of weighted inputs is used to measure the efficiency (Fig. 1).

$$ {\text{EFF}}_{i} = \frac{{\sum\nolimits_{r = 1}^{S} {u_{r} y_{rj} } }}{{\sum\nolimits_{i = 1}^{m} {v_{i} x_{ij} } }} $$

(2)

If m is the number of inputs for each DMU, S is the number of outputs for each DMU, and n is the number of DMUs, the fractional form of DEA-CCR model has a structure as described in model (3).

$$ \begin{aligned} & {\text{Max}}\; z_{o} = \frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{ro} } }}{{\sum\nolimits_{i = 1}^{m} {v_{i} x_{io} } }} \\ & {\text{S}}.{\text{t}}. \\ & \frac{{\sum\nolimits_{r = 1}^{s} {u_{r} y_{rj} } }}{{\sum\nolimits_{i = 1}^{m} {v_{i} x_{ij} } }} \le 1\quad j = 1,2, \ldots ,n \\ & u_{r} \ge 0,\quad v_{i} \ge 0 \\ \end{aligned} $$

(3)

A multiplier model was used to linearize the model (3). The model is input-oriented. In the present study, the dual of the multiplier model was used as input to rank each cluster (Cooper et al. 2006).

$$ \begin{aligned} & {\text{Max}} \;z_{o} = \sum\limits_{r = 1}^{s} {u_{r} y_{ro} } \\ & {\text{S}} . {\text{t}} .\\ & \sum\limits_{i = 1}^{m} {v_{i} x_{io} } = 1 \\ & \sum\limits_{r = 1}^{s} {u_{r} y_{rj} } - \sum\limits_{i = 1}^{m} {x_{ij} v_{i} } \le 0\quad j = 1,2, \ldots ,n \\ & u_{r} \ge 0 ,\quad v_{i} \ge 0 \\ \end{aligned} $$

(4)

Fig. 1

A decision-making unit with inputs and outputs

Invasive Weed Optimization

Invasive weed optimization is a bio-inspired numerical optimization algorithm that simulates the natural behavior of weeds in selection a suitable location for growth and construction of colonies. This is a population-oriented algorithm (Basak et al. 2013). The flowchart of the algorithm is shown in Fig. 2 (Abu-Al-Nadi et al. 2013).

Fig. 2

Flowchart for the IWO algorithm

To simulate the behavior of weeds (Fig. 2), the following points should be considered (Pahlavani et al. 2012):

Initializing a population

A limited number of seeds are dispersed over the search area (N0)

Reproduction

Each seed grows to be a flowering plant according to its fitness. Each member of the plant population can produce seeds depending on the lowest and highest fitness of its own colony. The number of seeds each plant produces increases linearly from the minimum possible value (S_min) to the maximum possible value (S_max). In other words, a plant produces seeds based on the highest fitness in its colony to ensure that the increase is linear. Figure 3 illustrates the procedure (Pahlavani et al. 2012) (Fig. 4).

Fig. 3

Seed production procedure in a colony of weeds

Fig. 4

A new framework for the selection of a portfolio of maintenance locations

Spatial dispersal

The produced seeds are dispersed with random normal distribution with a mean equal to zero and different variances over the search space so that they are near their parents and grow to a new plant. The standard deviation, σ, for the random function of the initial set of previously determined $\sigma_{\text{iter}}$ is reduced to the final value iteration $(\sigma_{\text{final}} )$ at each step. In simulations, Eq. 5 shows the satisfactory performance:

$$ \sigma_{\text{iter}} = \left( {\frac{{{\text{iter}}_{\hbox{max} } - {\text{iter}}}}{{{\text{iter}}_{\hbox{max} } }}} \right)^{n} \left( {\sigma_{\text{iter}} - \sigma_{\text{final}} } \right) + \sigma_{\text{final}} $$

(5)

where iter_max is the maximum number of iterations, σ_iter is the standard deviation in the current step, and n is the nonlinear index. We are certain that the distance of seeds from their parents decreases nonlinearly in each step.

Competitive exclusion

Reproduction continues to achieve the maximum number of plants (P_max). Now, only plants with higher fitness can survive and produce seeds, and the rest are eliminated.

The above steps continue to achieve the maximum number of plants and plants with highest fitness. This is the shortest way to achieve the optimal solution.

A new framework for multi-criteria location selection problem

Here, a new framework for multi-criteria location selection problem is presented. Previous approaches to multi-criteria location selection problem has focused on selecting a location from a set of locations. The methodology presented here is applicable in hybrid location selection condition. (Decision-maker selects more than one location.) The main objective of this study was to select a portfolio of locations for maintenance stations.

Determining problem indices

The indices influencing the selection of candidate locations to establish the maintenance stations are determined in the first stage using experts’ ideas.

Clustering

This stage is related to the input vectors of the criteria related to the candidate locations. These vectors are clustered using K-means algorithm. The output determines the candidate locations to establish the clustered maintenance stations.

Efficiency evaluation

The efficiency of the locations in each cluster was determined using the DEA-CCR model. The input to this stage includes the clustered candidate locations. The output of this stage includes the efficiency of the candidate locations in each cluster.

Mathematical modeling

A zero–one bi-objective programming model was developed. The first objective in model was to maximize the rank of the locations, and the second objective was to minimize the distance of maintenance stations from the studied locations. The constraint of the study was that at least one station maintenance must be in the neighborhood of the existing location. The input to this stage includes the efficiency of the candidate stations for maintenance activities in the clusters ad the optimized distance in each cluster.

Optimization

The Pareto solutions for risk and distance were obtained using the invasive weed optimization Algorithm.

Case study

A case study is presented to describe the hybrid DEA-based K-means and invasive weed optimization for facility location algorithm. This case was presented in an oil refinery to deploy repair and maintenance stations with the purpose of maximizing the efficiency of stations and minimizing the number of stations based on clusters at the same time. The oil refinery of the case study is under construction. Management follows the building of maintenance stations in refinery activities. According to the presented framework, the stages related to determining the optimal location of maintenance stations in the present case are as follows:

Determining problem indices

The indices influencing the selection of maintenance stations were determined in the first stage using experts’ ideas. These criteria include:

• C1: The score of space of each location for the construction of maintenance center.

• C2: Cost of construction

• C3: Professional association of the selected location with the maintenance activities of the stations.

• C4: Flexibility

Input data are summarized in Table 1. It should be noted that the information of input data was collected from an oil refinery Company.

Table 1 Input data

The scoring units are discrete for each of the data on Table 1, which are scored by experts.

Figure 5 shows the facility layout. According to the plan, the objective is to select the minimum number of locations for maintenance stations. However, stations have to cover all centers.

Fig. 5

Facility layout of maintenance stations

K-means Algorithm calculations

K-means clustering method was used to cluster the maintenance stations. The process of using this algorithm and the calculations of profile coefficient for the present case are as follows:

Silhouette index was used to calculate the optimal number of clusters. The results for clusters 2–7 are shown in Fig. 6. According to Fig. 6, the optimal number of clusters was checked through the Silhouette index. In all of the shapes indicated in Fig. 6, the value of this index did not fall short of zero. It shows that locations were not allocated to wrong clusters in any of the scenarios. In the double-cluster mode (the first state on the left), the Silhouette index is better than the single-cluster state due to being closer to one. It should be mentioned that the closer the Silhouette index is to one, the much farther the locations are from neighboring clusters. However, the investigated shape shows that many locations are placed in the cluster in the double-cluster mode. The tri-cluster mode is similar with a corrective trend (the second state on the right). Although the Silhouette index is greater than zero when there are five, six and seven clusters, the number of allocated locations to each cluster is less equal to the mode with four clusters (the third state on the left). Thus, clustering was based on the mode with four clusters. In this state, the number of locations is better than other states. Moreover, the Silhouette index approaches one.

Fig. 6

Calculations of the optimal number of clusters

Based on Silhouette index method, four clusters were selected. Result of K-means clustering algorithm is shown in Fig. 7. In fact, the resultant clusters placed the selected locations based on C1, C2, C3 and C4 in the four clusters. Therefore, the locations of repair and maintenance stations are investigated with respect to the four created clusters in this case.

Fig. 7

The result of data clustering using K-means algorithm

According to K-means algorithm, the locations 15, 14, 12, 10, 7, 5, 1 and 19 were placed in the first cluster, locations 2, 11, 16, 18 and 20 were placed in the second cluster, locations 8, 3 and 13 were placed in the third cluster, and locations 9, 6, 4 and 17 were placed in the fourth cluster.

DEA Modeling: Data envelopment analysis model was used to calculate the efficiency of each candidate location in each cluster. DEA model used in this study was the DEA–CCR input-oriented envelopment model. The first phase of the input-oriented DEA–CCR model for the first unit, which is located in the first cluster, is shown in model (6)

$$ \begin{aligned} & {\text{Min }}y_{0} = \theta , \\ & {\text{S}} . {\text{t}} .\\ & 11 \, \lambda_{1} + 16 \, \lambda_{2} + 2 \, \lambda_{3} + 19 \, \lambda_{4} + 14 \, \lambda_{5} + 5 \, \lambda_{6} + 9 \, \lambda_{7} + \, \lambda_{8} \, \ge 11, \\ & 2 \, \lambda_{1} + 6 \, \lambda_{2} + 5 \, \lambda_{3} + 4 \, \lambda_{4} + 5 \, \lambda_{5} + 9 \, \lambda_{6} + 6 \, \lambda_{7} + 7 \, \lambda_{8} \, \ge 2, \\ & - 5\;\varvec{\theta}\text{ + }5 \, \lambda_{1} + 5 \, \lambda_{2} + 5 \, \lambda_{3} + 5 \, \lambda_{4} + 2 \, \lambda_{5} + 9 \, \lambda_{6} + 5 \, \lambda_{7} + 5 \, \lambda_{8} \, \le \, 0, \\ & - 2000\;\varvec{\theta}+ 2000 \, \lambda_{1} + 2200 \, \lambda_{2} + 2500 \, \lambda_{3} + 1600 \, \lambda_{4} + 1900 \, \lambda_{5} + 2400 \, \lambda_{6} + 2700 \, \lambda_{7} + 1900 \, \lambda_{8} \, \le \, 0, \\ & \lambda_{j} \, \ge 0,\;\varvec{\theta}\;{\text{is}}\;{\text{free}} .\\ \end{aligned} $$

(6)

Second phase of the input-oriented CCR model (6) is presented as model (7):

$$ \begin{aligned} & {\text{Max }}S = s_{1}^{ + } + s_{2}^{ + } + s_{1}^{ - } + s_{2}^{ - } , \\ & {\text{s}} . {\text{t}} .\\ & 11\;\lambda_{1} + 16\;\lambda_{2} + 2\;\lambda_{3} + 19\;\lambda_{4} + 14\;\lambda_{5} + 5\;\lambda_{6} + 9\;\lambda_{7} + \lambda_{8} - \varvec{s}_{{\mathbf{1}}}^{ - } = 11, \\ & 2\;\lambda_{1} + 6\;\lambda_{2} + 5\;\lambda_{3} + 4 \, \lambda_{4} + 5 \, \lambda_{5} + 9 \, \lambda_{6} + 6 \, \lambda_{7} + 7 \, \lambda_{8} - \varvec{s}_{{\mathbf{2}}}^{ - } = 2, \\ & 5 \, \lambda_{1} + 5 \, \lambda_{2} + 5 \, \lambda_{3} + 5 \, \lambda_{4} + 2 \, \lambda_{5} + 9 \, \lambda_{6} + 5 \, \lambda_{7} + 5 \, \lambda_{8} + \varvec{s}_{{\mathbf{1}}}^{ + } \varvec{ = \theta }^{*} , \\ & 2000 \, \lambda_{1} + 2200 \, \lambda_{2} + 2500 \, \lambda_{3} + 1600 \, \lambda_{4} + 1900 \, \lambda_{5} + 2400 \, \lambda_{6} + 2700 \, \lambda_{7} + 1900 \, \lambda_{8} + \varvec{s}_{{\mathbf{2}}}^{ + } = {\mathbf{2000}}\;\varvec{\theta}^{*} , \\ & \lambda_{j} \ge 0,\quad \varvec{s}_{{\mathbf{1}}}^{ + } \ge 0,\quad \varvec{s}_{{\mathbf{2}}}^{ + } \ge 0,\quad \varvec{s}_{{\mathbf{1}}}^{ - } \ge 0,\quad \varvec{s}_{{\mathbf{2}}}^{ - } \ge {\mathbf{0}}. \\ \end{aligned} $$

(7)

Given the fact that 20 models should be written to determine the efficiency of 20 selected locations for the establishment of repair and maintenance stations, Model 3 was formulated for the first location according to Table 1. The dual form model is Model 2. The free variable is indicated by θ determining the efficiency of each location. In Model 3, the goal is to determine the efficiency of the first location. Given the fact that Location 1 was placed in the first cluster, its efficiency was modeled in comparison with Locations 5, 7, 10, 12, 14, 15 and 19. Therefore, the values of output variables (C3 and C4) and input variables (C1 and C2) of the other locations were not defined in Model 3 because they were not placed in the first cluster. In this model, λ_i indicates a ratio of inputs to outputs of all locations which are merged to create a virtual unit. In Model 3, the first and second constraints are output constraints. On the right side of the first and second constraints, numbers 2 and 11 indicate the first and second outputs of the first unit, respectively. Regarding the first and second constraints, the coefficients of the decision variable λ_i are the very output indices C3 and C4 (Table 1) for the locations existing in the first cluster. The third and fourth constraints of Model 3 are input constraints. On the left side of these constraints, numbers 5 and 2000 show the first and second inputs of the first unit, respectively. Regarding the third and fourth constraints, the coefficients of λ_i are the very input indices C1 and C2 (Table 1) for the locations existing in the first cluster.

Table 2 shows the efficiency of the candidate locations in each cluster using the input-oriented envelopment CCR-DEA.

Table 2 Calculation of the efficiency of each cluster

Bi-objective mathematical modeling

Having calculated the efficiency of the maintenance stations in each cluster, a bi-objective 0–1 programming model is designed at this stage with the aim of maximizing the efficiency of each cluster and minimizing the number of maintenance stations. The first objective function in this model optimizes the efficiency of the previous stages based on the created clusters. In the second objective function, the distance of each of the maintenance stations in the clusters is minimized. The limitations of this model are defined based on the neighborhood of maintenance stations in each cluster. The bi-objective programming model is presented as model (8).

$$ \begin{aligned} & {\text{Max}}\;z_{1} = 0.52x_{1} + x_{2} + x_{3} + x_{4} + 0.96x_{5} + x_{6} + 0.61x_{7} + x_{8} + x_{9} + x_{10} + 0.71x_{11} + x_{12} + x_{13} + x_{14} + 0.72x_{15} + 0.87x_{16} + 0.89x_{17} + x_{18} + x_{19} + x_{20} , \\ & {\text{Min}}\;z_{2} = x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} + x_{9} + x_{10} + x_{11} + x_{12} + x_{13} + x_{14} + x_{15} + x_{16} + x_{17} + x_{18} + x_{19} + x_{20} , \\ & {\text{S}} . {\text{t}} .\\ & x_{1} + x_{2} + x_{8} + x_{10} \ge 1, \\ & x_{1} + x_{2} + x_{3} + x_{7} + x_{8} \ge 1, \\ & x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} \ge 1, \\ & x_{3} + x_{4} + x_{5} \ge 1, \\ & x_{3} + x_{4} + \, x_{5} + x_{6} + x_{11} \ge 1, \\ & x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{9} + x_{11} + x_{12} + x_{13} + \, x_{14} \ge 1, \\ & x_{2} + x_{3} + x_{6} + \, x_{7} + x_{8} + x_{9} + x_{10} \, \ge 1, \\ & x_{1} + x_{2} + x_{7} + x_{8} + x_{10} \ge 1, \\ & x_{6} + x_{7} + x_{8} + x_{9} + x_{10} + x_{13} + x_{14} + x_{15} \ge 1, \\ & x_{1} + x_{7} + x_{8} + x_{9} + x_{10} + x_{15 \, } \ge 1, \\ & x_{5} + x_{6} + x_{11} + x_{12} + x_{17} + x_{20} \, \ge 1, \\ & x_{6} + x_{11} + x_{12} + x_{14} + x_{17} \ge 1, \\ & x_{6} + x_{9} + x_{13} + x_{14} \ge 1, \\ & x_{6} + x_{9} + x_{12} + \, x_{13} + x_{14} + x_{15} + x_{16} \, + x_{17} + x_{18} \ge 1, \\ & x_{9} + x_{10} + x_{14} + x_{15} \ge 1, \\ & x_{14} + x_{15} + x_{17} + x_{18} + x_{19} \ge 1, \\ & x_{11} + x_{12} + x_{14} + \, x_{16} + x_{17} + x_{19} + x_{20} \ge 1, \\ & x_{14} + x_{16} + x_{18} + x_{19} + x_{20} \ge 1, \\ & x_{16} + x_{17} + x_{18} + x_{19} + x_{20} \ge 1, \\ & x_{11} + x_{17} + x_{18} + x_{19} + x_{20} \ge 1, \\ & X_{ij} = \left\{ {0\;{\text{or}}\;1} \right\} \\ \end{aligned} $$

(8)

Optimization

Result of model (8) using the MOIWO algorithm is shown in Fig. 8. The running time of the algorithm was 160.4935 s.

Fig. 8

The Pareto solution for rank and distance

Table 3 shows the results of efficiency maximization and location minimization objective functions. According to the second row of this table, the maximum efficiency was calculated 13.09, and the corresponding minimum number of locations was 15 in addition to two optimal combinations of layouts. According to the third row, the objective function shows at least 4 optimal locations. In this case, the efficiency of objective function is 3.89.

Table 3 The results of solution based on the best result in an objective function

Figure 9 shows how to deploy each repair and maintenance station to maximize efficiency (blue asterisk) and minimize the number of locations (red squares).

Fig. 9

New layout

Conclusions

One of the main methods of multi-criteria selection is the multi-criteria location selection problem. Location selection using multi-criteria analysis techniques is an important strategic step in the production process of an industrial organization. A new methodology based on a combination of data mining algorithms, multi-criteria optimization and multiple attribute decision making was used to select an optimal portfolio of maintenance locations. For this purpose, the indices affecting the selection of maintenance locations were identified. Maintenance stations were placed in four clusters using the K-means data mining algorithm. The reason for selecting four clusters was the result of the Silhouette index method in determining the optimal number of clusters. The advantage of clustering maintenance stations using the K-means algorithm is that it allows for selecting maintenance stations from different portfolios. Each cluster was evaluated and ranked through the input-oriented DEA-CCR model. The efficiency of each maintenance station was separately analyzed using the input-oriented CCR-DEA model. A zero–one multi-objective programming model was developed for the Pareto optimal analysis of rank and distance. The Pareto optimal solutions for rank and distance were analyzed using the invasive weed optimization algorithm. Based on the case data and according to the results of using the K-means algorithm, it was found out that the research data should be investigated in four clusters instead of modeling and decision making based on one cluster. This study determines that if clustering methods are used before being analyzed by an initial decision matrix, more opportunities will be provided for the candidate locations in different clusters to achieve the efficiency and higher orders. In other words, since the cluster outputs determine that research data are not in one cluster, the analysis of the input vectors of the decision problem does not seem logical based on a decision table. This study was conducted for the combined selection of designated locations to do maintenance activities. The proposed method can be used in combined placement problems to determine different combinations of designated locations.