Introduction and literature review

Statistical control charts have been widely used in industries to monitor quality characteristics and states of processes. By distinguishing between common and special causes of variability, they determine the state of a process and generate a signal when the process moves to an out-of-control condition. Following a signal from a control chart, process engineers initiate a search to identify and remove the root causes of variation. However, due to the inertia property of control charts, the signaling time is different from the real time at which a process starts to be affected by special causes (change point) and in most cases, the change had really occurred much earlier than the signaling time. Despite the efficiency of control charts in monitoring process changes, they do not provide any specific information about the time and the root causes of process variation. Therefore, providing an accurate estimate of the change point would enable process engineers to eliminate the root causes in a quick manner and improve the quality of processes.

Many researchers proposed change-point estimates of processes with quality characteristics following various probability distributions. While Samuel et al. (1998a, b), Pignatiello and Samuel (2001), Ghazanfari et al. (2008), Perry et al. (2006, 2007), Perry and Pignatiello (2005, 2006, 2010), Fahmy and Elsayed (2006), and Noorossana and Shadman (2009) proposed procedures to estimate the change point in the parameters of univariate distributions, Nedumaran et al. (2000), Atashgar and Noorossana (2010), Niaki and Khedmati (2012, 2013, 2014a, b), and Sullivan and Woodall (2000) considered change-point estimations in the parameter vectors of multivariate distributions. However, in some applications, the quality of a process can be better characterized by a relationship between a response variable and one or more predictors. Such a relationship is commonly referred to as a profile and may be represented by a simple linear, a multiple linear, a polynomial, or a nonlinear regression model. Simple linear profiles are mostly used in calibration applications and are widely studied in the literature for both Phases I and II monitoring; see, for example, Kang and Albin (2000), Kim et al. (2003), Zhang et al. (2009), Saghaei et al. (2009), Mahmoud and Woodall (2004), Mahmoud et al. (2010), Soleimani et al. (2009), and Hossienifard et al. (2011). Besides, some authors including Mahmoud (2008), Jensen et al. (2008), Amiri et al. (2012), and Kazemzadeh et al. (2010) considered more complicated models such as multiple linear and polynomial regression profiles.

Although there exist remarkable research efforts on developing methods to monitor profiles in Phases I and II, only a few research works have been performed to estimate the change point of processes monitored by profiles. To name a few, Zou et al. (2007) proposed a maximum likelihood estimator of a step-change point in the parameters of a general linear profile in Phase II and showed their method works well. In another work, Zou et al. (2006) developed a likelihood ratio statistic to estimate a step-change point in the parameters of a simple linear profile in Phase I. In another work, Eyvazian et al. (2011) proposed a method based on the likelihood ratio approach to estimate the time of a step change in the parameters of a multivariate multiple linear regression profile in Phase II. Sharafi et al. (2013) proposed a maximum likelihood estimator of a step-change point in binary response profiles in which logistic regression was used to model the relationship between a binary response and explanatory variables. In another work, Sharafi et al. (2013) developed a maximum likelihood estimator for identifying step-change points in Phase-II monitoring of Poisson regression profiles. Interested readers are referred to Zand et al. (2013), Kazemzadeh et al. (2014), Keramatpour et al. (2013), and Sharafi et al. (2013) for more references.

Although in some applications the error terms in successive profiles are auto-correlated [see for example Jensen et al. (2008); Kazemzadeh et al. (2010); Noorossana et al. (2008); Zhang et al. (2014); Keramatpour et al. (2014); Niaki et al. (2014); Jensen and Birch (2009); Amiri et al. (2010); and Khedmati and Niaki (2015)], to the best of authors’ knowledge there has not been any research work on estimating the time of a step change in auto-correlated simple linear profiles in Phase II. Therefore, in this paper, a maximum likelihood estimator of a step change in the parameters of auto-correlated simple linear regression profiles is first proposed in which the auto-correlation structure between observations in each profile is assumed to follow a first-order auto-regressive, AR(1), model. Then, the performance of the proposed procedure is compared to one of the built-in change-point estimator of EWMA control chart, where three EWMA control charts are applied to monitor the parameters of an auto-correlated simple linear profile.

The organization of the rest of the paper is as follows: In the next section, the auto-correlated simple linear regression model and the transformation method to eliminate the effect of auto-correlation within each profile is described. The process is modeled and the maximum likelihood estimator of the change point is derived in “Process modeling and MLE derivation” section. The performance of the proposed change-point estimators is evaluated and is compared to one of the built-in estimator of EWMA chart in “Performance evaluation” section through some simulation experiments. An illustrative example is provided in “Cadinality and coverage performances of the confidence set estimator” section to demonstrate the application of the proposed methodology. Finally, concluding remarks are presented in “An illustrative example” section.

Auto-correlated simple linear regression model

For the jth sample collected over time, the observations are denoted by (x i , y ij ), i = 1, 2, …, n, where it is assumed there exist an auto-correlation between the error terms and that within-profile observations at different values of the predictor variable x are modeled by a first-order auto-regressive, AR(1), model. Based on this model, when the process is in statistical control, the relationship between the response variable y ij , the predictor variable and the error terms is

$$\begin{aligned} y_{ij} &= A_{0} + A_{1} x_{i} + \varepsilon_{ij} , \hfill \\ \varepsilon_{ij} &= \varphi \varepsilon_{{\left( {i - 1} \right)j}} + a_{ij} , \hfill \\ \end{aligned}$$
(1)

where A 0 and A 1 are model parameters, ɛ ij ’s are the correlated error terms, 0 < φ < 1 is the auto-correlation coefficient, and a ij ’s are independent and identically distributed (iid) normal random variables with mean zero and variance σ 2, i.e., N(0, σ 2). We assume that the x values are fixed and constant from profile to profile. Moreover, as the change-point estimation is aimed in Phase-II monitoring of auto-correlated simple linear profiles, the in-control values of the parameters A 0, A 1, σ 2, and φ are assumed known.

Considering the auto-correlation structure between the error terms, observations in successive profiles can be expressed by \(y_{ij} = A_{0} + A_{1} x_{i} + \varepsilon_{ij}\) and \(y_{{\left( {i - 1} \right)j}} = A_{0} + A_{1} x_{{\left( {i - 1} \right)}} + \varepsilon_{{\left( {i - 1} \right)j}}\). Deriving the correlated error terms ɛ ij and ɛ (i−1)j from these equations and replacing them into the AR(1) auto-correlation structure shown in Eq. (1) leads to

$$y_{ij} - \left( {A_{0} + A_{1} x_{i} } \right) = \varphi \left[ {y_{{\left( {i - 1} \right)j}} - \left( {A_{0} + A_{1} x_{{\left( {i - 1} \right)}} } \right)} \right] + a_{ij} .$$
(2)

According to Eq. (2), there exist auto-correlations between observations within each profile. Soleimani et al. (2009) showed that the existing auto-correlation between the error terms within each profile affects the performance of the control charts for simple linear profiles. Therefore, they applied a transformation to eliminate the effect of auto-correlation. In this transformation, one first transforms the observations using Eq. (3).

$$y^{\prime}_{ij} = y_{ij} - \varphi y_{{\left( {i - 1} \right)j}} .$$
(3)

Then, she/he replaces the observations y ij and y (i−1)j by their equivalents in Eq. (1). This leads to a simple linear regression model with independent error terms as

$$y^{\prime}_{ij} = A_{0} \left( {1 - \varphi } \right) + A_{1} \left( {x_{i} - \varphi x_{i - 1} } \right) + \left( {\varepsilon_{ij} - \varphi \varepsilon_{{\left( {i - 1} \right)j}} } \right).$$
(4)

Finally, the following model is obtained

$$y^{\prime}_{ij} = A^{\prime}_{0} + A^{\prime}_{1} x^{\prime}_{i} + a_{ij} ,$$
(5)

where \(A^{\prime}_{0} = A_{0} \left( {1 - \varphi } \right)\), \(A^{\prime}_{1} = A_{1}\), \(x^{\prime}_{i} = x_{i} - \varphi x_{i - 1} ,\) and a ij ’s are independent normal random variables with mean zero and variance σ 2.

Now, the EWMA-3 method, first introduced by Kim et al. (2003), is applied to monitor the transformed simple linear profile with uncorrelated observations in Phase II. Several researchers showed that the EWMA-3 procedure outperforms other methods such as T 2 and EWMA/R for most of the shift magnitudes in each of the parameters (see Kim et al. (2003); Soleimani et al. (2009) for more details). In this method, the x′-values are coded such that the average coded value is zero. To do this, they are subtracted from their average, i.e., \(x^{\prime\prime} = x^{\prime} - \bar{x^{\prime}}\). Applying this method, the least-squares estimators of the intercept and slope will be independent and consequently, separate control charts can be used to monitor the three parameters of the model. The model after the transformation becomes

$$y^{\prime}_{ij} = B_{0} + B_{1} x^{\prime\prime}_{i} + a_{ij} ,$$
(6)

in which \(B_{0} = A^{\prime}_{0} + A^{\prime}_{1} \bar{x^{\prime}}\), \(B_{1} = A^{\prime}_{1},\) and \(x^{\prime\prime}_{i} = \left( {x^{\prime}_{i} - \bar{x^{\prime}}} \right)\).

For the EWMA control chart designed to monitor the intercept B 0, the estimator of the intercept for the jth sample (b 0(j)) in the EWMA statistics is

$${\text{EWMA}}_{\text{I}} \left( j \right) = \theta b_{0} \left( j \right) + \left( {1 - \theta } \right){\text{EWMA}}_{\text{I}} \left( {j - 1} \right),$$
(7)

where \(\theta \left( {0 < \theta \le 1} \right)\) is the smoothing parameter and EWMAI(0) = B 0. The lower and the upper control limits of this control chart are given in Eq. (8), where as long as the EWMAI statistics are within them, the intercept of the profile is in statistical control.

$$\begin{aligned} {\text{LCL}}_{\text{I}} &= B_{0} - L_{\text{I}} \sigma \sqrt {{\theta \mathord{\left/ {\vphantom {\theta {\left[ {\left( {2 - \theta } \right)\left( {n - 1} \right)} \right]}}} \right. \kern-0pt} {\left[ {\left( {2 - \theta } \right)\left( {n - 1} \right)} \right]}}} {\quad \text{and}} \hfill \\ {\text{UCL}}_{\text{I}} &= B_{0} + L_{\text{I}} \sigma {{\sqrt{\theta \mathord{\left/ {\vphantom {\theta {\left[ {\left( {2 - \theta } \right)\left( {n - 1} \right)} \right]}}} \right. \kern-0pt} {\left[ {\left( {2 - \theta } \right)\left( {n - 1} \right)} \right]}}}}, \hfill \\ \end{aligned}$$
(8)

in which L I (>0) is chosen to give a specified in-control ARL.

For the EWMA control chart designed to monitor the slope B 1, the estimator of the slope for the jth sample (b 1(j)) in the EWMA statistics is

$${\text{EWMA}}_{\text{S}} \left( j \right) = \theta b_{1} \left( j \right)\, + \,\left( {1 - \theta } \right){\text{EWMA}}_{\text{S}} \left( {j - 1} \right),$$
(9)

where \(\theta \left( {0 < \theta \le 1} \right)\) is the smoothing parameter and EWMAS(0) = B 1. The lower and the upper control limits of this control chart are given in Eq. (10) and as long as the EWMAS statistics are within these control limits, the slope of the profile is in statistical control.

$$\begin{aligned} {\text{LCL}}_{\text{S}} & = B_{1} - L_{\text{S}} \sigma \sqrt {{\theta \mathord{\left/ {\vphantom {\theta {\left[ {\left( {2 - \theta } \right)\sum\limits_{i = 2}^{n} {\mathop {x_{i}^{''} }\nolimits^{2} } } \right]}}} \right. \kern-0pt} {\left[ {\left( {2 - \theta } \right)\sum\limits_{i = 2}^{n} {\mathop {x_{i}^{''} }\nolimits^{2} } } \right]}}} \;{\quad \text{and}} \\ {\text{UCL}}_{\text{S}} & = B_{1} + L_{\text{S}} \sigma \sqrt {{\theta \mathord{\left/ {\vphantom {\theta {\left[ {\left( {2 - \theta } \right)\sum\limits_{i = 2}^{n} {\mathop {x_{i}^{''} }\nolimits^{2} } } \right]}}} \right. \kern-0pt} {\left[ {\left( {2 - \theta } \right)\sum\limits_{i = 2}^{n} {\mathop {x_{i}^{''} }\nolimits^{2} } } \right]}}} , \\ \end{aligned}$$
(10)

in which L S(>0) is chosen to give a specified in-control ARL.

The third EWMA control chart is used to monitor the error variance σ 2. In this control chart, the estimator of the error variance based on residuals MSE j , is used in the EWMA statistics as

$${\text{EWMA}}_{\text{E}} \left( j \right) = \hbox{max} \left\{ {\theta \left( {{\text{MSE}}_{j} - 1} \right) + \left( {1 - \theta } \right){\text{EWMA}}_{\text{E}} \left( {j - 1} \right),\ln \sigma^{2} } \right\},$$
(11)

where \(\theta \left( {0 < \theta \le 1} \right)\) is the smoothing parameter and EWMAS(0) = ln σ 2. The upper control limit of this control chart is given in Eq. (12).

$${\text{UCL}}_{\text{E}} = L_{\text{E}} \sqrt {{{\theta \text{var} \left( {{\text{MSE}}_{j} } \right)} \mathord{\left/ {\vphantom {{\theta \text{var} \left( {{\text{MSE}}_{j} } \right)} {\left( {2 - \theta } \right)}}} \right. \kern-0pt} {\left( {2 - \theta } \right)}}} ,$$
(12)

in which L E(>0) is chosen to give a specified in-control ARL, and \({\text{var}}\left( {{\text{MSE}}_{j} } \right) = \frac{{2\sigma^{4} }}{n - 1}\) [see Soleimani et al. (2009) for more details].

Process modeling and MLE derivation

As long as the statistics falls within the lower and upper control limits, the process is assumed in statistical control with known in-control parameters B 00, B 10, and \(\sigma_{0}^{2}\). Following an unknown point in time τ, a change occurs and process moves to an out-of-control state with unknown parameters B 01, B 11, and \(\sigma_{1}^{2}\). We assume that the change type is a step change and when this type of change occurs, the process remains at the new level until the special causes are identified and removed. Based on this model, during the formation of the profiles j = 1, 2, …, τ the process is in control with known in-control parameters B 00, B 10, and \(\sigma_{0}^{2}\) while, for profiles j =  τ + 1, τ + 2,…, T the parameters change to out-of-control values B 01, B 11, and \(\sigma_{1}^{2},\) where T indicates the signaling time. This model is used to derive the maximum likelihood estimator of the change point, denoted by \(\hat{\tau }\).

Considering the change point to occur at τ, the likelihood function is given by

$$L\left( {\tau ,B_{01} , B_{11} , \sigma_{1}^{2} |y} \right) = \mathop \prod \limits_{j = 1}^{\tau } \mathop \prod \limits_{i = 1}^{n - 1} \frac{1}{{\sigma_{0} \sqrt {2\pi } }}e^{{ - \frac{{\left( {y^{\prime}_{ij} - B_{00} - B_{10} x^{\prime\prime}_{i} } \right)^{2} }}{{2\sigma_{0}^{2} }}}} \times \mathop \prod \limits_{j = \tau + 1}^{T} \mathop \prod \limits_{i = 1}^{n - 1} \frac{1}{{\sigma_{1} \sqrt {2\pi } }}e^{{ - \frac{{\left( {y^{\prime}_{ij} - B_{01} - B_{11} x^{\prime\prime}_{i} } \right)^{2} }}{{2\sigma_{1}^{2} }}}} .$$
(13)

The logarithm of the likelihood function in Eq. (13) is

$$\begin{aligned} \ln L\left( {\tau ,B_{01} , B_{11} , \sigma_{1}^{2} |y} \right) = & - \frac{{\tau \left( {n - 1} \right)}}{2}\ln \left( {2\pi \sigma_{0}^{2} } \right) - \frac{1}{{2\sigma_{0}^{2} }}\mathop \sum \limits_{j = 1}^{\tau } \mathop \sum \limits_{i = 1}^{n - 1} \left( {y^{\prime}_{ij} - B_{00} - B_{10} x^{\prime\prime}_{i} } \right)^{2} \\ - \frac{{\left( {T - \tau } \right)\left( {n - 1} \right)}}{2}\ln \left( {2\pi \sigma_{1}^{2} } \right) - \frac{1}{{2\sigma_{1}^{2} }}\mathop \sum \limits_{j = \tau + 1}^{T} \mathop \sum \limits_{i = 1}^{n - 1} \left( {y^{\prime}_{ij} - B_{01} - B_{11} x^{\prime\prime}_{i} } \right)^{2} . \\ \end{aligned}$$
(14)

There are four unknown parameters \(\tau , B_{01} , B_{11},\) and \(\sigma_{1}^{2}\) in the log-likelihood function in Eq. (14) that have to be estimated. At first, the maximum likelihood estimation of the parameters \(B_{01} , B_{11},\) and \(\sigma_{1}^{2}\) is obtained for all possible values of the change point in the range 0 ≤ t < T, by the following equations

$$\begin{aligned} \hat{B}_{{11}} & = \frac{{\left( {S_{{x^{{\prime \prime }} y^{\prime } }} } \right)_{{t,T}} }}{{\left( {S_{{x^{{\prime \prime }} x^{{\prime \prime }} }} } \right)_{{t,T}} }}, \\ \hat{B}_{{01}} & = \left( {\overline{{y^{\prime } }} _{{ij}} } \right)_{{t,T}} - \hat{B}_{{11}} \left( {\overline{{x^{\prime } }} _{{ij}} } \right)_{{t,T}} \quad {\text{and}} \\ \hat{\sigma }_{1}^{2} & = \frac{{\sum\nolimits_{{j = t + 1}}^{T} {\sum\nolimits_{{i = 1}}^{{n - 1}} {\left( {y_{{ij}}^{\prime } - \hat{B}_{{01}} - \hat{B}_{{11}} x_{i}^{{\prime \prime }} } \right)^{2} } } }}{{\left( {T - t} \right)\left( {n - 1} \right)}}, \\ \end{aligned}$$
(15)

where (.) t,T is calculated based on the profiles t to T. Then, using the estimated parameters in Eq. (15), the MLE of the change point denoted by \(\hat{\tau }\) is obtained as

$$\hat{\tau } = \arg \hbox{max} \left\{ { - \frac{{t\left( {n - 1} \right)}}{2}\ln \left( {2\pi \sigma_{0}^{2} } \right) \,-\, \frac{1}{{2\sigma_{0}^{2} }}\mathop \sum \limits_{j = 1}^{t} \mathop \sum \limits_{i = 1}^{n - 1} \left( {y^{\prime}_{ij} - B_{00} - B_{10} x^{\prime\prime}_{i} } \right)^{2} - \frac{{\left( {T - t} \right)\left( {n - 1} \right)}}{2}\ln \left( {2\pi \hat{\sigma }_{1}^{2} } \right) \,-\, \frac{{\left( {T - t} \right)\left( {n - 1} \right)}}{2}} \right\} .$$
(16)

The estimated change point \(\hat{\tau }\) is the point that maximizes Eq. (16) for values of \(0 \le t < T\).

The built-in change-point estimator of EWMA control chart suggested by Nishina (1992) is also employed in this research to evaluate the performance of the proposed change-point estimator. Nishina (1992) proposed an estimator to identify the change point in processes monitored by EWMA control charts, following a signal from the control chart. Since the process is monitored using three separate EWMA control charts, the Nishina’s approach is applied to the control chart that issues an out-of-control signal. In this regard, if the EWMAI control chart issues an out-of-control signal, the estimated change point, denoted by \(\hat{\tau }_{\text{EWMA}}\), is

$$\hat{\tau }_{\text{EWMA}} = \left\{ {\begin{array}{*{20}c} {\hbox{max} \left\{ {j: {\text{EWMA}}_{\text{I}} \left( j \right) \le B_{00} } \right\} {\quad\text{if}} \quad{\text{EWMA}}_{\text{I}} \left( T \right) > {\text{UCL}}_{\text{I}} } \\ {\hbox{max} \left\{ {j: {\text{EWMA}}_{\text{I}} \left( j \right) \ge B_{00} } \right\} {\quad\text{if}} \quad{\text{EWMA}}_{\text{I}} \left( T \right) < {\text{LCL}}_{\text{I}} } \\ \end{array} } \right.$$
(17)

In other words, if an increase in the intercept is investigated by the control chart, the change point is estimated using \(\hat{\tau }_{\text{EWMA}} = \hbox{max} \left\{ {j: {\text{EWMA}}_{\text{I}} \left( j \right) \le B_{00} } \right\},\) while if a decrease in the intercept is investigated, the change point is estimated by \(\hat{\tau }_{\text{EWMA}} = \hbox{max} \left\{ {j: {\text{EWMA}}_{\text{I}} \left( j \right) \ge B_{00} } \right\}\). If the EWMAS control chart issues an out-of-control signal, the change point is estimated by

$$\hat{\tau }_{\text{EWMA}} = \left\{ {\begin{array}{*{20}c} {\hbox{max} \left\{ {j: {\text{EWMA}}_{\text{S}} \left( j \right) \le B_{10} } \right\} {\quad\text{{if} \quad{EWMA}}}_{\text{S}} \left( T \right) > {\text{UCL}}_{\text{S}} } \\ {\hbox{max} \left\{ {j: {\text{EWMA}}_{\text{S}} \left( j \right) \ge B_{10} } \right\} {\quad\text{if \quad{EWMA}}}_{\text{S}} \left( T \right) < {\text{LCL}}_{\text{S}} } \\ \end{array} } \right.$$
(18)

Finally, if the EWMAE control chart issues an out-of-control signal, the estimated change point is obtained by

$$\hat{\tau }_{\text{EWMA}} = \hbox{max} \left\{ {j: {\text{EWMA}}_{\text{E}} \left( j \right) \le \ln \sigma_{0}^{2} } \right\}.$$
(19)

In the next section, the performance of the proposed change-point estimator is compared to one of the above built-in EWMA estimator through some simulation experiments, where all programming tasks are performed using the MATLAB 7 software.

Performance evaluation

In this section, the performance of the proposed methods in estimating the time of a step change in the parameters of auto-correlated simple linear profiles is evaluated through some simulation experiments. In the simulation studies, the underlying model is considered as

$$\begin{aligned} y_{ij} = 3 + 2x_{i} + \varepsilon_{ij} , \hfill \\ \varepsilon_{ij} = \varphi \varepsilon_{{\left( {i - 1} \right)j}} + a_{ij} \hfill \\ \end{aligned},$$
(20)

where a ij ’s are independent normal variables with mean zero and variance one, and the fixed x values are set equal to 2, 4, 6, and 8. In the EWMA-3 control chart, the smoothing parameter is 0.2 and the values of the parameters \((L_{I} , L_{S} , L_{E} )\) are set equal to (3.014, 3.012, 3.870), respectively, to obtain the overall in-control ARL of approximately 200 under φ = 0.1, φ = 0.2, φ = 0.4, φ = 0.5, φ = 0.7, and φ = 0.9 auto-correlation coefficient values.

Considering a change to occur at time τ = 50, the observations for the first 50 profiles are randomly generated based on the in-control process given in Eq. (20) in which all parameters are known and in statistical control. However, following the 51st profile, observations are randomly generated from an out-of-control process with a step shift in the parameters as

$$\begin{aligned} A_{01} = A_{00} + \lambda \sigma_{0} , \hfill \\ A_{11} = A_{10} + \beta \sigma_{0} , \hfill \\ \sigma_{1}^{2} = \gamma \sigma_{0}^{2} . \hfill \\ \end{aligned}.$$
(21)

The transformations are used, and the corresponding statistic for each profile is calculated and plotted in the EWMA-3 control chart. Following a genuine out-of-control signal, the change-point estimators in Eqs. (16–19) are applied to determine the time of the change. This procedure is replicated 10,000 times to obtain the averages, the standard deviations, and the precision performances of the estimated change point for all auto-correlation coefficients (φ = 0.1, φ = 0.2, φ = 0.4, φ = 0.5, φ = 0.7, and φ = 0.9) under investigation.

Table 1 contains the averages and standard deviations of the change-point estimates under a step shift in the intercept from A 00 to A 01 = A 00 + λσ 0 for both estimators under different auto-correlation coefficients. Based on the results in Table 1, while both estimators provide satisfactory results in terms of the expected length of a simulation run, E(T) = ARL + 50, the proposed MLE of the change point provides more accurate estimates than the built-in estimator of EWMA control chart, for almost all shift magnitudes and auto-correlation coefficients. Besides, the estimated change points for small shifts are closer to the real change point and that an increase in change-point estimates for larger auto-correlation coefficients results in an increase in the average run length (ARL). In other words, as auto-correlation coefficient gets larger the ARL and hence the expected length of run increases and consequently larger estimates of change point are obtained.

Table 1 Estimated change points and standard deviations of the two change-point estimators for a step shift in the intercept based on different auto-correlation coefficients
Full size table

Moreover, the precision performances are reported in Table 2 for a step shift in the intercept, in which the probabilities \(P\left( {\left| {\hat{\tau } - \tau } \right| = 0} \right)\), \(P\left( {\left| {\hat{\tau } - \tau } \right| \le 1} \right)\), \(P\left( {\left| {\hat{\tau } - \tau } \right| \le 3} \right),\) and \(P\left( {\left| {\hat{\tau } - \tau } \right| \le 5} \right)\) are denoted by P0, P1, P3, and P5, respectively. The results in Table 2 show that while \(\hat{\tau }_{EWMA}\) provides more precise estimates in comparison to \(\hat{\tau }\) for small shifts, as the shift magnitudes increase the precision performance of \(\hat{\tau }\) increases and \(\hat{\tau }\) outperforms \(\hat{\tau }_{EWMA}\).

Table 2 Estimated precision performances of the two change-point estimators for a step shift in the intercept based on different auto-correlation coefficients
Full size table

The results of averages, standard deviations, and precision performances of the estimated change points under a step shift in the slope parameter from A 10 to A 11 = A 10 + βσ 0 are summarized in Tables 3 and 4. Based on the results in Table 3, the proposed MLE of the change point provides adequately accurate estimates for almost all shift values and auto-correlation coefficients. In fact, in addition to better results of \(\hat{\tau }\) in comparison to E(T), it provides more accurate results than \(\hat{\tau }_{EWMA}\). Moreover, the results in Table 4 show better precision for \(\hat{\tau }_{EWMA}\) for small shift values and better precision for \(\hat{\tau }\) as shift values increase.

Table 3 Estimated change points and standard deviations of the two change-point estimators for a step shift in the slope based on different auto-correlation coefficients
Full size table
Table 4 Estimated precision performances of the two change-point estimators for a step shift in the slope based on different auto-correlation coefficients
Full size table

Finally, Tables 5 and 6 contain the averages, the standard deviations, and the precision performances of the change-point estimates under a step shift in the error variance from \(\sigma_{0}^{2}\) to \(\sigma_{1}^{2} = \gamma \sigma_{0}^{2}\). Again, the results show that the proposed change-point estimator \(\hat{\tau }\) provides more accurate estimates compared to \(\hat{\tau }_{EWMA}\) for shifts of almost any magnitude and all auto-correlation coefficients. Furthermore, \(\hat{\tau }\) provides more precise results than \(\hat{\tau }_{EWMA}\) especially for large shift values.

Table 5 Estimated change points and standard deviations of the two change-point estimators for a step shift in the error variance based on different auto-correlation coefficients
Full size table
Table 6 Estimated precision performances of the two change-point estimators for a step shift in the error variance and for different auto-correlation coefficients
Full size table

In summary, the proposed MLE of a step change in the parameters of an auto-correlated simple linear profile provides adequately accurate and precise estimates of the change point, regardless of shift magnitude and auto-correlation coefficient. In addition, the results obtained from simulation experiments indicate that \(\hat{\tau }\) outperforms \(\hat{\tau }_{EWMA}\) for almost all shift values where in most cases, \(\hat{\tau }_{EWMA}\) underestimates the real change point.

Cardinality and coverage performances of the confidence set estimator

In this section, the cardinality and coverage performance of the confidence set estimator for the process change point are evaluated. Confidence sets for the change point provide a window of the possible change points that cover the true change point of the process. Consequently, process engineers can identify the true change point more quickly. According to Box and Cox (1964), the confidence set of the change point estimates are obtained as

$${\text{CS}} = \left\{ {t: \ln L\left( t \right) > \ln L\left( {\hat{\tau }} \right) - D} \right\},$$
(22)

in which \({ \ln }L\left( {\hat{\tau }} \right)\) represents the maximum of the log-likelihood function for all values of 0 ≤ t < T. Based on Eq. (22), t is included in the confidence set if the value of the log-likelihood function at t is greater than the maximum of the log-likelihood function minus a reference value D. In this paper, the cardinality and coverage percent of the confidence set estimator is calculated for different reference values of D = 1, D = 3, and D = 5. The results for a step shift in the intercept of the profile are reported in Table 7.

Table 7 Cardinality and coverage probabilities for different reference values under shift in the intercept
Full size table

Based on the results in Table 7, for reference value of D = 3 and shift of size λ = 1.2, for example, the confidence set estimator provides an expected cardinality of 9.617 and coverage rate of 0.9994; that is, the confidence set contains the true change point with high probability of 0.9994.

An illustrative example

The application of the proposed approach is demonstrated in this section using a numerical example. Consider an in-control model as

$$\begin{aligned} y_{ij} &= 3 + 2x_{i} + \varepsilon_{ij} , \hfill \\ \varepsilon_{ij} &= 0.25\varepsilon_{{\left( {i - 1} \right)j}} + a_{ij} , \hfill \\ \end{aligned}$$
(23)

where a ij ’s are independent normal variables with mean zero and variance one, and the fixed x values are set equal to 2, 4, 6, and 8. Moreover, the smoothing parameter is set equal to 0.2 and the values of the parameters \((L_{\text{I}} , L_{\text{S}} , L_{\text{E}} )\) are set equal to (3.014, 3.012, 3.870) to obtain the overall in-control ARL of 200.

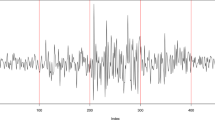
Considering the change to occur at 20th profile, the first 20 profiles come from the in-control process and thereafter, a shift of size λ = 1 is induced in the intercept of the model. The values of the statistics in Eqs. (7), (9), and (11) are calculated and plotted on the control charts until a signal is issued at profile 24 by the EWMAI control chart. At this time, the two methods are employed to estimate the change point. Figure 1 shows the EWMAI statistics plotted on the control chart in which a signal is generated at profile 24.

Fig. 1
figure 1

The EWMA I control chart with a shift in the intercept and the estimate of change point using both methods

Full size image

Based on the results in Fig. 1, the MLE of the change point is obtained at t = 20 while the EWMA built-in estimator of change point is obtained at t = 17. Consequently, \(\hat{\tau } = 20\) is the estimated change point of the process obtained from the proposed change-point estimator while \(\hat{\tau }_{\text{EWMA}} = 17\) is the estimated change point obtained from the built-in estimator of EWMA control chart. As a result, applying the proposed method, process engineers can search around the estimated change-point and find the root causes of process variation in a quick manner.

Conclusions

In this paper, a maximum likelihood estimator of a step change in the parameters of auto-correlated simple linear profiles was derived, in which the auto-correlation structure between observations in each profile was assumed to be a first-order auto-regressive model. Applying a transformation technique, the effect of auto-correlation was first eliminated and then, each of the three parameters of a simple linear profile was monitored separately by an EWMA control chart until a signal was generated. At this time, the estimator was applied to estimate the true change point. Comparing the performance of the proposed MLE of the change point with built-in change-point estimator of the EWMA chart, we showed that the proposed MLE provides adequately accurate and precise estimates of the change point and outperforms the built-in estimator of the EWMA chart, regardless of the shift magnitude and the auto-correlation coefficient.

While we showed that an increase in the auto-correlation coefficient leads to an increase in the average run length and hence an increase in the change-point estimates, developing a method to estimate the change point that is not affected by the auto-correlation coefficient may be an interesting area for future research. Moreover, one may extend the proposed method for other auto-correlated profiles such as ARMA(p, q) auto-correlated multivariate linear profiles as well. In addition, the effect of smoothing parameter, decreasing shifts in the parameters, and the confidence set of the proposed estimators can be investigated in further studies.