Markov modeling and reliability analysis of urea synthesis system of a fertilizer plant

Abstract

This paper deals with the Markov modeling and reliability analysis of urea synthesis system of a fertilizer plant. This system was modeled using Markov birth–death process with the assumption that the failure and repair rates of each subsystem follow exponential distribution. The first-order Chapman–Kolmogorov differential equations are developed with the use of mnemonic rule and these equations are solved with Runga–Kutta fourth-order method. The long-run availability, reliability and mean time between failures are computed for various choices of failure and repair rates of subsystems of the system. The findings of the paper are discussed with the plant personnel to adopt and practice suitable maintenance policies/strategies to enhance the performance of the urea synthesis system of the fertilizer plant.

Introduction

The system reliability has great significance in recent years due to competitive environment. Reliability is defined as the ability of a system to perform the required function under stated conditions for a specified period of time. The reliability of a complex system can be obtained by either increasing the capacity of the system or providing sufficient redundant part(s) with perfect switch over devices. Kumar and Tewari (2008, 2009) presented a simulation model for evaluating the performance of CO-shift conversion system and urea decomposition system in a fertilizer plant. Dhillon and Singh (1981) and Kumar et al. (1989, 2007) used Markov model for performance analysis of paper and fertilizer plants. Arora and Kumar (1997) discussed the availability analysis of steam and powder generation systems of thermal power plants. Gupta and Tewari (2011) presented the availability model for a thermal power plant. Khanduja et al. (2012) presented the steady-state behavior and maintenance planning of bleaching system of a paper plant. Kumar and Tewari (2011) discussed the mathematical modeling and performance optimization of CO₂ cooling system of a fertilizer plant using the genetic algorithm. Dhople et al. (2014) provided a framework to analyze Markov reward models used in system performability analysis. Tewari et al. (2012) computed the steady-state availability and performance optimization for the crystallization unit of a sugar plant by using genetic algorithm. Kiilumen and Frisk (2014) developed a method to examine the long-term reliability of an anisotropic conductive adhesive (ACA)-attached polyethylene terephthalate (PET) flex-on-board (FOB) assembly for industrial application used in harsh environments. Ahmed et al. (2014) provided a risk-based stochastic modeling approach using a Markov decision process to assess the availability of a processing unit, which is referred to as the risk-based availability Markov model (RBAMM). Kumar et al. (2011) discussed the performance analysis of the furnace draft air cycle of a thermal power plant. Kadiyan et al. (2012) discussed the availability and reliability analysis of an uncaser system for a brewery plant. Singh and Goyal (2013) presented a methodology to study the steady-state behavior of repairable mechanical biscuit shaping system pertaining to a biscuit-manufacturing plant. Kumar and Mudgil (2014) discussed the availability analysis of the ice cream-making unit of a milk plant.

The literature revealed that the methods used by the different authors involve complex computations and the problem of determining long-run or steady-state availability of the system has been extensively studied. In this paper, a numerical method, i.e., Runge–Kutta fourth-order method is used to compute the MTBF and reliability of the urea synthesis system of a fertilizer plant. The values of failure and repair rates of all the subsystems of urea synthesis system were collected from maintenance history sheets and discussion with maintenance personnel of a fertilizer plant situated at Panipat, Haryana (India). The fertilizer plant comprises many systems, viz. urea synthesis system, urea decomposition system, urea crystallization system, urea prilling system, etc. The urea synthesis system is important for a fertilizer plant. This paper has been organized into six sections. The present section is the introductory type including the concerned literature review. In second section presents the “Mathematical aspects of reliability and availability”, whereas the third section concerned with “System description, assumptions and notations”. In fourth section deals with “Mathematical modeling of urea synthesis system”. “Performance analysis of the system” concerns in the fifth section. Finallly, sixth section deals with “Discussion and conclusion”.

Mathematical aspects of reliability and availability

Reliability

Reliability is the probability for failure-free operation of a system during a given interval of time, i.e., it is a measure of success for a failure-free operation. The reliability of a component may be calculated as:

$$ R\left( t \right) = 1 - e^{ - \alpha t} $$

where α is the constant failure rate of the component (per hour) and t is the operation time (hour).

$$ {\text{Reliability}} = e^{{\left[ { - \frac{\text{Time}}{\text{MTBF}}} \right]}} $$

Availability

Availability is the probability that a component or system is performing its required function at a given point in time when used under stated operating conditions. It is calculated by the ratio between lifetime and total time between failures of the equipment.

Mean time between failures (MTBF)

MTBF is the amount of failures per million hours for a component. It is commonly used as a variable in reliability and maintainability analysis as

$$ {\text{MTBF }} = \mathop \smallint \limits_{0}^{\infty } R\left( t \right){\text{d}}t = \mathop \smallint \limits_{0}^{\infty } e^{ - \beta t} {\text{d}}t = \frac{1}{\beta }. $$

Markov approach

Arora and Kumar (1997), Bradley and Dawson (1998), Dhillon and Singh (1981), Kumar et al. (1993, 2007) and Bhamare et al. (2008) used the Markov approach for availability analysis of different process plants. According to Markov, if P₀(t) represents the probability of zero occurrences in time t, the probability of zero occurrences in time (t + ∆t) is given by the Eq. (1)

$$ P_{ 0} \left( {t + \Delta t} \right) \, = \, \left( { 1- \alpha t} \right) \, P_{ 0} \left( t \right). $$

(1)

Similarly,

$$ P_{ 1} \left( {t + \Delta t} \right) = \beta \Delta t \, P_{ 0} \left( t \right) + \left( { 1- \alpha \Delta t} \right) \, P_{ 1} \left( t \right), $$

(2)

where α is the failure rate and β is the repair rate of the component or subsystem respectively.

The Eq. (2) shows that the probability of one occurrence in time $(t + \Delta t)$ is composed of two parts:

• probability of zero occurrences in time t multiplied by the probability of one occurrence in time interval $\Delta t$ and

• probability of one occurrence in time t multiplied by the probability of no occurrences in the interval $\Delta t$.

After simplifying and taking ∆t → 0, the Eq. (2) is reduced to

$$ P_{1}^{\prime } \left( t \right) + \beta P_{1} \left( t \right) = \alpha \, P_{o} \left( t \right). $$

(3)

Using the concept used in Eq. (3), the equations for transient and steady states are derived.

System description, assumptions and notations

System description

The urea synthesis system comprises a compressor used to compress the carbon dioxide, two reciprocating pumps used to boost the pressure of liquid ammonia and heaters used to heat ammonia gas. In this process, the CO₂ gas and liquid ammonia (NH₃) available from the ammonia production process are fed to the urea synthesis reactor. In the reactor these gases react to form urea in gaseous form. The urea synthesis system comprises five subsystems arranged in series as (Fig. 1):

• 1. Subsystem A₁: It has CO₂ booster compressor as a single unit arranged in series. Its failure causes the complete failure of the system.

• 2. Subsystem A₂: It has CO₂ compressor as a single unit arranged in series. Failure of this subsystem causes the complete failure of the system.

• 3. Subsystem A₃: It consists of three NH₃ pre-heaters units arranged in series. Failure of any one of these causes the complete failure of the system.

• 4. Subsystem H: It consists of four liquid ammonia feed pumps arranged in parallel. Two pumps remain operative in parallel and the other two in cold standby. Failure of three pumps at a time will cause complete failure of the system.

• 5. Subsystem L: It consists of three recycle solution feed pumps arranged in parallel. Failure of any one unit reduces the capacity of the system, but complete failure occurs when failure of all units takes place at a time.

Fig. 1

Flow diagram of the urea synthesis system

Assumptions

• The failure and repair rates are constant over time, statistically independent of each other and there are no simultaneous failures among the subsystems as stated by Kumar and Kumar (2011).

• There are sufficient repair or replacement facilities, i.e., no waiting time to start the repairs. The failure or repair of the system follows exponential distribution as stated by Srinath (1994).

• A repaired system is as good as new, performance-wise, as stated by Khanduja et al. (2008).

• The switchover devices used for standby subsystems are perfect.

Notations

:

Full working state of the system

:

Reduced state of the system

:

Failed state of the system

P ₀ (t):

Probability of the system working with full capacity at time t

P ₁ (t), P ₆ (t):

Probability of the system in cold standby state

P _2, (t) to P _5, (t), P _7, (t),P _8, (t):

Probability of the system in reduced capacity state

P ₉ (t) to P ₄₁ (t):

Probability of the system in failed state

α _i; i = 1,2,3,4,5:

Mean failure rates of A₁, A₂, A₃, H and L, respectively

ß _i; i = 1,2,3,4,5:

Mean repair rates of A₁, A₂, A₃, H and L, respectively, and

d/dt:

derivative w.r.t. t

Mathematical modeling of the urea synthesis system

The mathematical modeling of the system is carried out using simple probabilistic considerations and Chapman–Kolmogorov differential equations are developed based on Markov birth–death process. The Chapman–Kolmogorov differential equations are derived by using the mnemonic rule as stated by Khanduja et al. (2008). According to the mnemonic rule, the derivative of the probability of every state is equal to the sum of all probability flows which comes from other states to the given state minus the sum of all probability flows which goes out from the given state to the other states. The transition diagram (Fig. 2) depicts a simulation model showing all the possible states of the urea synthesis system.

Fig. 2

Transition diagram of the urea synthesis system

Thus, the equations for transient state and steady state of the urea synthesis system are derived as follows.

Transient state

Mathematical Eqs. (4)–(17) are developed by applying Markov birth–death process to each state one by one out of 41 states of transition diagram (Fig. 2) as explained by Garg et al. (2010a, b):

$$ \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} } \right)P_{0} \left( t \right) = \beta_{1} P_{9} \left( t \right) + \beta_{2} P_{10} \left( t \right) + \beta_{3} P_{11} \left( t \right) + \beta_{4} P_{2} \left( t \right) + \beta_{5} P_{1} \left( t \right) $$

(4)

$$ \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{5} } \right)P_{1} \left( t \right) = \beta_{1} P_{12} \left( t \right) + \beta_{2} P_{13} \left( t \right) + \beta_{3} P_{14} \left( t \right) + \beta_{5} P_{6} \left( t \right) + \beta_{4} P_{3} \left( t \right) \, + \alpha_{5} P_{0} \left( t \right) $$

(5)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{4} } \right)P_{2} \left( t \right) & = \beta_{1} P_{15} \left( t \right) + \beta_{2} P_{16} \left( t \right) + \beta_{3} P_{17} \left( t \right) \\ & \quad + \beta_{4} P_{4} \left( t \right) + \beta_{5} P_{3} \left( t \right) + \alpha_{4} P_{0} \left( t \right) \\ \end{aligned} $$

(6)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{5} + \beta_{4} } \right)P_{3} \left( t \right) & = \beta_{1} P_{18} \left( t \right) + \beta_{2} P_{19} \left( t \right) + \beta_{3} P_{20} \left( t \right) \\ & \quad + \beta_{4} P_{5} \left( t \right) + \alpha_{4} P_{1} \left( t \right) + \alpha_{5} P_{2} \left( t \right) \\ \end{aligned} $$

(7)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{4} } \right)P_{4} \left( t \right) & = \beta_{1} P_{21} \left( t \right) + \beta_{2} P_{22} \left( t \right) + \beta_{3} P_{23} \left( t \right) \\ & \quad + \beta_{4} P_{24} \left( t \right) + \beta_{5} P_{5} \left( t \right) + \alpha_{4} P_{2} \left( t \right) \\ \end{aligned} $$

(8)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{4} + \beta_{5} } \right)P_{5} \left( t \right) & = \beta_{1} P_{25} \left( t \right) + \beta_{2} P_{26} \left( t \right) + \beta_{3} P_{27} \left( t \right) \\ & \quad + \beta_{4} P_{40} \left( t \right) + \beta_{5} P_{8} \left( t \right) + \alpha_{4} P_{3} \left( t \right) + \alpha_{5} P_{4} \left( t \right) \\ \end{aligned} $$

(9)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{5} } \right)P_{6} \left( t \right) & = \beta_{1} P_{28} \left( t \right) + \beta_{2} P_{29} \left( t \right) + \beta_{3} P_{30} \left( t \right) \\ & \quad + \beta_{5} P_{31} \left( t \right) + \beta_{4} P_{7} \left( t \right) + \alpha_{5} P_{1} \left( t \right) \\ \end{aligned} $$

(10)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{5} + \beta_{4} } \right)P_{7} \left( t \right) & = \beta_{1} P_{32} \left( t \right) + \beta_{2} P_{33} \left( t \right) + \beta_{3} P_{34} \left( t \right) \\ & \quad + \beta_{5} P_{41} \left( t \right) + \beta_{4} P_{8} \left( t \right) + \alpha_{5} P_{3} \left( t \right) + \alpha_{4} P_{6} \left( t \right) \\ \end{aligned} $$

(11)

$$ \begin{aligned} \left( {{\text{d}}/{\text{d}}t + \mathop \sum \limits_{i = 1}^{5} \alpha_{i} + \beta_{5} + \beta_{4} } \right)P_{8} \left( t \right) & = \beta_{1} P_{35} \left( t \right) + \beta_{2} P_{36} \left( t \right) + \beta_{3} P_{37} \left( t \right) \\ & \quad + \beta_{5} P_{39} \left( t \right) + \beta_{4} P_{38} \left( t \right) + \alpha_{5} P_{5} \left( t \right) + \alpha_{4} P_{7} \left( t \right) \\ \end{aligned} $$

(12)

$$ ({\text{d}}/{\text{d}}t + \beta_{1} )P_{i} \left( t \right) = \alpha_{1} P_{j} \left( t \right), $$

(13)

where i = 9,12,15,18,21,25,28,32,35 and j = 0,1,2,3,4,5,6,7,8, respectively.

$$ ({\text{d}}/{\text{d}}t + \beta_{2} )P_{i} \left( t \right) = \alpha_{2} P_{j} \left( t \right), $$

(14)

where i = 10, 13, 16, 19, 22, 26, 29, 33, 36 and j = 0, 1, 2, 3, 4, 5, 6, 7, 8, respectively.

$$ ({\text{d}}/{\text{d}}t + \beta_{3} )P_{i} \left( t \right) = \alpha_{3} P_{j} \left( t \right), $$

(15)

where i = 11, 14, 17, 20, 23, 27, 30, 34, 37 and j = 0, 1, 2, 3, 4, 5, 6, 7, 8, respectively.

$$ ({\text{d}}/{\text{d}}t + \beta_{4} )P_{i} \left( t \right) = \alpha_{4} P_{j} \left( t \right), $$

(16)

where i = 24, 40, 39 and j = 4, 5, 8, respectively.

$$ ({\text{d}}/{\text{d}}t + \beta_{5} )P_{i} \left( t \right) = \alpha_{5} P_{j} \left( t \right), $$

(17)

where i = 31, 41, 38 and j = 6, 7, 8, respectively.

The initial conditions are:

$$ P_{\text{j}} (0) = \left \{ \begin{array}{*{20}c} {1,} & {\text{if j = 1}} \\ {0 ,} & {{\text{if j}} \ne 1} \\ \end{array} \right.$$

(18)

The system of differential Eqs. (4)–(17) with initial conditions given by Eq. (18) was solved by Runge–Kutta fourth-order method. The numerical computations were carried out by taking time t = 0 to t = 360 days for different choices of failure and repair rates of the subsystems. The data regarding failure and repair rates of all the subsystems were taken from the plant personnel as stated earlier.

Reliability R(t) of the system is the sum of the reliabilities of the system working under full capacity and reduced state, i.e.,

$$ R\left( t \right) = P_{0} \left( t \right) + P_{1} \left( t \right) + P_{2} \left( t \right) + P_{3} \left( t \right) \ldots + P_{8} \left( t \right). $$

(19)

Equation (19) is used to compute the reliability of the urea synthesis system, where P₀(t) is the probability of the system working with full capacity, P ₁(t) and P ₆(t) are the probability of the system working under cold standby state and P ₂(t), P ₃(t), P ₄(t), P ₅(t), P ₇(t) and P ₈(t) are the probability of the system working with reduced capacity.

Steady state

Arora and Kumar (1997) stated that in process plant or industries, the management is interested in getting the long-run availability of the system. The steady-state probabilities of the system are obtained by imposing the following restrictions: d/dt → 0, as t → ∞. Thus, the long-run availability, i.e., A(∞) of the urea synthesis system is obtained by putting derivative of all probabilities equal to zero, i.e.,

$$ \beta_{1} P_{i} = \alpha_{1} P_{j}, $$

(20)

where i = 9,12,15,18,21,25,28,32,35 and j = 0,1,2,3,4,5,6,7,8 respectively.

$$ \beta_{2} P_{i} = \alpha_{2} P_{j} , $$

(21)

where i = 9,12,15,18,21,25,28,32,35 and j = 0,1,2,3,4,5,6,7,8, respectively.

$$ \beta_{3} P_{i} = \alpha_{3} P_{j} , $$

(22)

where i = 9,12,15,18,21,25,28,32,35 and j = 0,1,2,3,4,5,6,7,8. respectively.

$$ \beta_{4} P_{i} = \alpha_{4} P_{j} , $$

(23)

where i = 24, 40, 39 and j = 4, 5, 8, respectively.

$$ \beta_{5} P_{i} = \alpha_{5} P_{j} , $$

(24)

where i = 31, 41, 38 and j = 6, 7, 8, respectively.

Thus, by putting the values of probabilities from Eqs. (20)–(24) in Eqs. (4)–(17),

finally, we get

$$ C_{1} P_{0} = \beta_{5} P_{1} + \beta_{4} P_{2} \quad {\text{where }}C_{1} = \alpha_{5} + \alpha_{4} , $$

(25)

$$ C_{2} P_{1} = \beta_{5} P_{6} + \beta_{4} P_{3} + \alpha_{5} P_{0} \quad {\text{where }}C_{2} = \, C_{1} + \beta_{5} , $$

(26)

$$ C_{3} P_{2} = \beta_{5} P_{3} + \alpha_{4} P_{0} + \beta_{4} P_{4} \quad {\text{where }}C_{3} = \, C_{1} + \beta_{4} , $$

(27)

$$ C_{4} P_{3} = \alpha_{4} P_{1} + \alpha_{5} P_{2} + \beta_{5} P_{7} + \beta_{4} P_{5} \quad {\text{where }}C_{4} = \, C_{3} + \beta_{5} , $$

(28)

$$ C_{5} P_{4} = \beta_{5} P_{5} + \alpha_{4} P_{2} \quad {\text{where }}C_{5} = \alpha_{5} + \beta_{4} , $$

(29)

$$ C_{6} P_{5} = \beta_{5} P_{8} + \alpha_{4} P_{3} + \alpha_{5} P_{4} \quad {\text{where }}C_{6} = \, C_{5} + \beta_{5} , $$

(30)

$$ C_{7} P_{6} = \beta_{4} P_{7} + \alpha_{1} P_{1} \quad {\text{where }}C_{7} = \alpha_{4} + \beta_{5} , $$

(31)

$$ C_{8} P_{7} = \beta_{4} P_{8} + \alpha_{4} P_{6} + \alpha_{5} P_{3} \quad {\text{where}}_{{}} C_{8} = \, C_{7} + \beta_{4} , $$

(32)

$$ C_{9} P_{8} = \alpha_{4} P_{7} + \alpha_{5} P_{5} \quad {\text{where }}C_{9} = \beta_{5} + \beta_{4} . $$

(33)

Solving these equations recursively,

$$ P_{1} = C_{17} P_{0} , $$

(34)

where $C_{17} = \, C_{14} + C_{15} + C_{16} / \, \left( {1 + C_{12} } \right) \, + C_{11} / \, (C_{13} / \, \left( {1 + C_{12} } \right) \, + C_{10} ;$

$$ P_{2} = C_{19} P_{0} , $$

(35)

where $C_{19} = \, \left( {C_{1} - \left( {\beta_{5} C_{16} } \right)} \right)/\beta_{4} ;$

$$ P_{3} = C_{18} P_{0} , $$

(36)

where $C_{18} = \left( {C_{13} /\left( {1 + C_{12} } \right)C_{17} } \right) - C_{16} ;$

$$ P_{4} = C_{21} P_{0} , $$

(37)

where C ₂₁ = ((C ₃ C ₁₉) − α ₄ − (β ₅ C ₁₈))/C ₃;

$$ P_{5} = C_{22} P_{0} , $$

(38)

where C ₂₂ = ((C ₅ C ₂₁) – (α ₄ C ₁₉))/β ₅;

$$ P_{6} = C_{20} P_{0} , $$

(39)

where C ₂₀ = ((C ₂ C ₁₇) – α ₅ – (β ₄ C ₁₈))/β ₅;

$$ P_{7} = C_{23} P_{0} , $$

(40)

where C ₂₃ = ((C ₇ C ₂₀) – (α ₅ C ₁₇))/β ₅;

$$ P_{8} = C_{24} P_{0} , $$

(41)

where C ₂₄ = ((α ₄ C ₂₃) + (α ₅C₂₂)).

$$ \begin{aligned} C_{31} & = \, (\alpha_{4} /C_{4} ) - (\alpha_{5} C_{5} )/\left( {C_{4} \beta_{4} } \right)) + ((\left( {C_{7} C_{2} } \right) + (\alpha_{5} \beta_{5} ))/\beta_{4} ) - C_{5} + \alpha_{4} , \\ C_{10} & = 1/ \, \left( {1 + C_{7} \beta_{4} + \, \left( {\left( {\beta_{4} C_{5} } \right)/C_{3} } \right)} \right) \, C_{31} , \\ C_{32} & = \, ((C_{7} \alpha_{5} )/\beta_{4} ) \, + \, (\alpha_{5} C_{1} ) - (((\beta_{4} C_{5} \alpha_{4} )/C_{3} ) - (C_{5} C_{1} )) \, /\beta_{5} , \\ C_{11} & = 1/ \, (1 + C_{7} \beta_{4} + \, ((\beta_{4} C_{5} )/C_{3} ))C_{32} , \\ C_{12} & = [(C_{8} C_{7} )/ \, (\alpha_{5} \alpha_{3} ) \, + \, \left( {\alpha_{4} \beta_{4} } \right)/ \, \left( {\alpha_{5} \beta_{5} } \right) - (\alpha_{5} C_{5} )/C_{3} - \left( {\beta_{4} \alpha_{4} } \right) \, / \, ((\alpha_{5} \beta_{5} C_{9} ))) \, ((C_{4} + \, ((\beta_{4} C_{5} )/C_{3} )))], \\ C_{13} & = [(C_{2} / \, \left( {\alpha_{5} \beta_{5} } \right)) \, (((C_{8} C_{7} \beta_{5} )/\beta_{4} ) - \left( {\alpha_{4} } \right)) - ((C_{8} /\beta_{4} ) \, + \, \left( {\left( {\alpha_{5} \alpha_{4} } \right)/\beta_{4} } \right) \, + \, (\alpha_{4} /C_{9} ))], \\ C_{14} & = \left( {1/ \, \left( {\beta_{4} \beta_{5} } \right)} \right) \, ((C_{8} C_{7} ) \, + \, (C_{1} \alpha_{5} \alpha_{4} )), \\ C_{15} & = (\left( {\alpha_{4} \beta_{4} \beta_{4} } \right)/ \, (\beta_{5} \beta_{5} C_{9} \alpha_{5} ))((\alpha_{5} C_{5} )/C_{3} - C_{1} ), \\ C_{16} & = (\alpha_{4} /\beta_{5} ) \, (1 + \, ((\alpha_{5} C_{5} )/C_{3} ) \, + \, \left( {C_{1} /C_{9} } \right)). \\ \end{aligned} $$

The probability of full working capacity, i.e., P ₀ is determined by using normalizing condition: (i.e., sum of the probabilities of all working states, reduced capacity and failed states is equal to 1), i.e.,

$$ \begin{gathered} \mathop \sum \limits_{i = 0}^{41} P_{i} = 1\quad \, i.e.\, \, P_{0} N = \, 1 \hfill \\ P_{0} = \, N^{ - 1} , \hfill \\ \end{gathered} $$

where

$$ \begin{aligned} N & = [\left( {1 + \, C_{17} + \, C_{18} + \, C_{19} + \, C_{20} + \, C_{21} + \, C_{22} + \, C_{23} + \, C_{24} } \right)(1 + \alpha_{1} /\beta_{1} \\ & \quad + \alpha_{2} /\beta_{2} + \alpha_{3} /\beta_{3} ) + \alpha_{4} /\beta_{4} )\left( {1 + \, C_{21} + \, C_{24} + \, C_{22} } \right) \, + \alpha_{5} /\beta_{5} (1 + \, C_{20} \\ & \quad + \, C_{24} + \, C_{23} )]. \\ \end{aligned} $$

Now, the steady state availability A(∞) of urea synthesis system may be obtained as summation of all working and reduced capacity state probabilities, i.e.,

$$ \begin{aligned} A\left( \infty \right) \, & = \mathop \sum \limits_{i = 0}^{8} P_{i} , \\ A\left( \infty \right) \, & = \, P_{0} + \, P_{1} + \, P_{2} + \, P_{3} + \, P_{4} + \, P_{5} + \, P_{6} + \, P_{7} + \, P_{8} , \\ A\left( \infty \right) & = \left( {1 + C_{17} + C_{18} + C_{19} + C_{20} + C_{21} + C_{22} + C_{23} + C_{24} } \right)/N, \\ A\left( \infty \right) & = \left( {1 + C_{17} + C_{18} + C_{19} + C_{20} + C_{21} + C_{22} + C_{23} + C_{24} } \right)/[(1 + \, C_{17} + \, C_{18} \\ & \quad + C_{19} + C_{20} + C_{21} + C_{22} + C_{23} + C_{24} )(1 + \alpha_{1} /\beta_{1} + \alpha_{2} /\beta_{2} + \alpha_{3} /\beta_{3} ) \\ & \quad + \alpha_{4} /\beta_{4} )\left( {1 + \, C_{21} + \, C_{24} + \, C_{22} } \right) \, + \alpha_{5} /\beta_{5} \left( {1 + \, C_{20} + \, C_{24} + \, C_{23} } \right)]. \\ \end{aligned} $$

(42)

Eq. (42) is used to get the long-run availability of the urea synthesis system.

Performance analysis of the system

This section includes the following

• The computation of long-run availability of the system.

• The computation of reliability and mean time between failures (MTBF) of the system.

Long-run availability of the system

The long-run availability of the system is computed by using Eq. (42), and the effect of change in failure and repair rates of subsystems on long-run availability of the system is presented in Tables 1, 2, 3, 4 and 5.

Table 1 Effect of failure and repair rates of subsystem A₁ on the long-run availability of the system

Table 2 Effect of failure and repair rates of subsystem A₂ on the long-run availability of the system

Table 3 Effect of failure and repair rates of subsystem A₃ on the long-run availability of the system

Table 4 Effect of failure and repair rates of subsystem H on long-run availability of the system

Table 5 Effect of failure and repair rates of subsystem L on the long-run availability of the system

Effect of failure and repair rates of subsystem A₁ on long-run availability of the system

The effect of failure and repair rates of subsystem A₁ on long-run availability of the system is studied by varying their values as α ₁ = 0.004, 0.005, 0.006, 0.007 and β ₁ = 0.35, 0.4, 0.45, 0.5. The failure and repair rates of other subsystems are kept constant as α ₂ = 0.005, α ₃ = 0.001, α ₄ = 0.002, α ₅ = 0.004, β ₂ = 0.1, β ₃ = 0.5, β ₄ = 0.1, β ₅ = 0.4. The long-run availability of the system is calculated using these data and the results are shown in Table 1. Table 1 shows that increase in failure rate (α ₁) of subsystem A ₁ causes decrease in long-run availability of the system from 0.794 to 0.559 % approximately, but increase in repair rate (β ₁) of subsystem A₁ causes increase in long-run availability of the system from 0.32 to 0.56 %.

Effect of failure and repair rates of subsystem A₂ on long-run availability of the system

The effect of failure and repair rates of subsystem A₂ on long-run availability of the system is studied by varying their values as α ₂ = 0.004, 0.005, 0.006, 0.007 and β ₂ = 0.05, 0.1, 0.15, 0.2. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₃ = 0.001, α ₄ = 0.002, α ₅ = 0.004, β ₁ = 0.4, β ₃ = 0.5, β ₄ = 0.1, β ₅ = 0.4. Table 2 shows that increase in failure rate (α ₂) of subsystem A ₂ causes decrease in long-run availability of the system from 5.16 to 1.418 % approximately, but increase in repair rate (β ₂) of subsystem A ₂ causes increase in long-run availability of the system from 5.76 to 9.93 %.

Effect of failure and repair rates of subsystem A₃ on long-run availability of the system

The effect of failure and repair rates of subsystem A₃ on long-run availability of the system is studied by varying their values as α ₃ = 0.0005, 0.001, 0.0015, 0.002 and β ₃ = 0.4, 0.5, 0.6, 0.7. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₄ = 0.002, α ₅ = 0.004, β ₁ = 0.4, β ₂ = 0.1, β ₄ = 0.1, β ₅ = 0.4. Table 3 shows that increase in failure rate (α ₃) of subsystem A ₃ causes decrease in long-run availability of the system from 0.299 to 0.221 % approximately, but increase in repair rate (β ₃) of subsystem A₃ causes increase in long-run availability of the system from 0.03 to 0.10 %.

Effect of failure and repair rates of subsystem H on long-run availability of the system

The effect of failure and repair rates of subsystem H on long-run availability of the system is studied by varying their values as α ₄ = 0.001, 0.002, 0.003, 0.004 and β ₄ = 0.05, 0.1, 0.15, 0.2. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₃ = 0.001, α ₅ = 0.004, β ₁ = 0.4, β ₂ = 0.1, β ₃ = 0.5, β ₅ = 0.4. Table 4 shows that increase in failure rate (α ₄) of subsystem H causes decrease in long-run availability of the system from 0.06 to 0.123 % approximately, but increase in repair rate (β ₄) of subsystem H causes decrease in long-run availability of the system from 0.032 to 0.095 %.

Effect of failure and repair rates of subsystem L on long-run availability of the system

The effect of failure and repair rates of subsystem L on long-run availability of the system is studied by varying their values as α ₅ = 0.003, 0.004, 0.005, 0.006 and β ₅ = 0.3, 0.4, 0.5, 0.6. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₃ = 0.001, α ₄ = 0.002, β ₁ = 0.4, β ₂ = 0.1, β ₃ = 0.5, β ₄ = 0.1. Table 5 shows that increase in failure rate (α ₅) of subsystem L causes decrease in long-run availability of the system from 0.547 to 0.384 % approximately, but increase in repair rate (β ₅) of subsystem L causes increase in long-run availability of the system from 0.21 to 0.37 %.

Reliability of the system

Some methods such as Laplace transformation, Lagrange’s and matrix methods are available to solve the governing differential equations, but these methods are not advisable for use if the system is complex and has a large number of differential equations. Therefore, Runge–Kutta fourth-order method is used to solve these differential equations.

Effect of failure and repair rates of subsystem A₁ on the reliability of the system

The effect of failure rates of subsystem A ₁ on the reliability of the system is studied by varying their values as α ₁ = 0.004, 0.005, 0.006, 0.007 at β ₁ = 0.4. The failure and repair rates of other subsystems are kept constant as α ₂ = 0.005, α ₃ = 0.001, α ₄ = 0.002, α ₅ = 0.004, β ₂ = 0.1, β ₃ = 0.5, β ₄ = 0.1, β ₅ = 0.4. The reliability of the system is calculated with these data and the results are shown in Table 6. This table shows that the reliability of the system decreases by 0.019 % approximately with the increase of time. However, it decreases from 0.7032 to 0.7015 % approximately and MTBF decreases from 339 to 336.7 days when the failure rate varies from 0.004 to 0.007.

Table 6 Effect of failure and repair rates of subsystem A₁ on the reliability of the system

The effect of repair rates of subsystem A ₁ on the reliability of the system is studied by varying their values as β ₁ = 0.3, 0.4, 0.5, 0.6 at α ₁ = 0.005. The failure and repair rates of other subsystems are kept constant as α ₂ = 0.005, α ₃ = 0.001, α ₄ = 0.002, α ₅ = 0.004, β ₂ = 0.1, β ₃ = 0.5, β ₄ = 0.1, β ₅ = 0.4. The reliability of the system is calculated with these data and the results are shown in Table 6. This table shows that the reliability of the system decreases by 0.185 % approximately with the increase of time. However, it increases from 0.7864 to 0.790 % approximately and MTBF increases from 336.97 to 339.62 days when the failure rate varies from 0.3 to 0.6.

Effect of failure and repair rates of subsystem A₂ on the reliability of the system

The effect of failure rates of subsystem A ₂ on the reliability of the system is studied by varying their values as α ₂ = 0.004, 0.005, 0.006, 0.007 at β ₂ = 0.1. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₃ = 0.001, α ₄ = 0.002, α ₅ = 0.004, β ₁ = 0.4, β ₃ = 0.5, β ₄ = 0.1, β ₅ = 0.4. The reliability of the system is calculated with these data and the results are shown in Table 7. This table shows that the reliability of the system decreases from 0.253 to 0.149 % approximately with the increase of time. However, it decreases from 2.76 to 2.66 % approximately and MTBF decreases from 332 to 313 days when the failure rate varies from 0.004 to 0.007.

Table 7 Effect of failure and repair rates of subsystem A₂ on the reliability of the system

The effect of repair rates of subsystem A₂ on the reliability of the system is studied by varying their values as β ₂ = 0.05, 0.1, 0.15, 0.2 at α ₂ = 0.005. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₃ = 0.001, α ₄ = 0.002, α ₅ = 0.004, β ₁ = 0.4, β ₃ = 0.5, β ₄ = 0.1, β ₅ = 0.4. The reliability of the system is calculated with these data and the results are shown in Table 7. This table shows that the reliability of the system decreases from 1.832 to 0.007 % approximately with the increase of time. However, it increases from 5.23 to 7.0 % approximately and MTBF increases from 323.68 days to 346.36 days when the repair rate varies from 0.05 to 0.2.

Effect of failure and repair rates of subsystem A₃ on the reliability of the system

The effect of failure rates of subsystem A₃ on the reliability of the system is studied by varying their values as α ₃ = 0.0005, 0.001, 0.0015, 0.002 at β ₃ = 0.5. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₄ = 0.002, α ₅ = 0.004, β ₁ = 0.4, β ₂ = 0.1, β ₄ = 0.1, β ₅ = 0.4. The reliability of the system is calculated with these data and results are shown in Table 8. This table shows that the reliability of the system decreases by 0.185 % approximately with the increase of time. However, it decreases by 0.282 % approximately and MTBF decreases from 338.6 days to 337.65 days when the failure rate varies from 0.0005 to 0.002.

Table 8 Effect of failure and repair rates of subsystem A₃ on the reliability of the system

The effect of repair rates of subsystem A₃ on the reliability of the system is studied by varying their values as β ₃ = 0.4, 0.5, 0.6, 0.7 at α ₃ = 0.001. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₄ = 0.002, α ₅ = 0.004, β ₁ = 0.4, β ₂ = 0.1, β ₄ = 0.1, β ₅ = 0.4. The reliability of the system is calculated with these data and results are shown in Table 8. This table shows that the reliability of the system decreases by 0.185 % approximately with the increase of time. However, it increases by 0.101 % approximately and MTBF increases from 338.13 to 338.47 days when the repair rate varies from 0.4 to 0.7.

Effect of failure and repair rates of subsystem H on the reliability of the system

The effect of failure rates of subsystem (H) on the reliability of the system is studied by varying their values as α ₄ = 0.001, 0.002, 0.003, 0.004 at β ₄ = 0.1. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₃ = 0.001, α ₅ = 0.004, β ₁ = 0.4, β ₂ = 0.1, β ₃ = 0.5, β ₅ = 0.4. The reliability of the system is calculated with these data and results are shown in Table 9. This table shows that the reliability of the system decreases from 0.197 to 0.165 % approximately with the increase of time. However, it decreases from 0.013 to 0.001 % and MTBF decreases from 338.32 to 338.27 days when the failure rate varies from 0.001 to 0.004.

Table 9 Effect of failure and repair rates of subsystem H on the reliability of the system

The effect of the repair rates of subsystem H on the reliability of the system is studied by varying their values as β ₄ = 0.05, 0.1, 0.15, 0.2 at α ₄ = 0.002. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₃ = 0.001, α ₅ = 0.004; β ₁ = 0.4, β ₂ = 0.1, β ₃ = 0.5, β ₅ = 0.4. The reliability of the system is calculated with these data and results are shown in Table 9. This table shows that the reliability of the system decreases from 0.197 to 0.168 % approximately with the increase of time. However, it increases from 0.0002 to 0.0125 % and MTBF increases from 338.27 to 338.31 days when the repair rate varies from 0.05 to 0.2.

Effect of failure and repair rates of subsystem L on the reliability of the system

The effect of failure rates of subsystem L on the reliability of the system is studied by varying their values as α ₅ = 0.003, 0.004, 0.005, 0.006 at β ₅ = 0.4. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₃ = 0.001, α ₄ = 0.002, β ₁ = 0.4, β ₂ = 0.1, β ₃ = 0.5, β ₄ = 0.1. The reliability of the system is calculated with these data and results are shown in Table 10. This table shows that the reliability of the system decreases from 0.197 to 0.156 % approximately with the increase of time. However, it decreases from 0.0215 to 0.0019 % approximately and MTBF decreases from 338.34 days to 338.27 days when the failure rate varies from 0.003 to 0.006.

Table 10 Effect of failure and repair rates of subsystem L on the reliability of the system

The effect of repair rates of subsystem (L) on the reliability of the system is studied by varying their values as β ₅ = 0.3, 0.4, 0.5, 0.6 at α ₅ = 0.004. The failure and repair rates of other subsystems are kept constant as α ₁ = 0.005, α ₂ = 0.005, α ₃ = 0.001, α ₄ = 0.002; β ₁ = 0.4, β ₂ = 0.1, β ₃ = 0.5, β ₄ = 0.1. The reliability of the system is calculated with these data and the results are shown in Table 10. This table shows that the reliability of the system decreases from 0.197 to 0.168 % approximately with the increase of time. However, it increases by 0.008 % and MTBF increases from 338.28 days to 338.27 days when the repair rate varies from 0.3 to 0.6.

Effect of failure and repair rates of subsystems on the long-run availability of the system

Table 11 shows the effect of change in failure and repair rates of subsystems on change (%) in the long-run availability of the system. Table 11 concludes that the change (%) in the long-run availability of the system is maximum with the change in failure and repair rate of subsystem A₂ and the same is shown in Fig. 3.

Table 11 Effect of failure and repair rates of subsystems on the long-run availability of the system

Fig. 3

Effect of failure and repair rate of subsystems on long-run availability of the system

Effect of failure and repair rates of subsystems on the reliability of the system

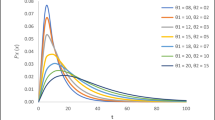
Table 12 shows the effect of change in failure and repair rates of subsystems on change (%) in reliability of the system. Table 12 concludes that the change (%) in reliability of the system is maximum with the change in failure and repair rate of subsystem A₂ and the same is shown in Fig. 4a, b. Figure 5 shows the effect of failure and repair rate of subsystem A₂ on system reliability (%).

Table 12 Effect of failure and repair rates of subsystems on the reliability of the system

Fig. 4

a Effect of failure rate of subsystems on the reliability of the system. b Effect of repair rate of subsystems on the reliability of the system

Fig. 5

Effect of failure and repair rate of subsystem A₂ on system reliability (%)

Discussion and conclusion

The proposed method is easy for use for in the complex system having a large number of differential equations and it helps to compute the long-run availability, reliability and mean time between failures (MTBF) of the urea synthesis system of the fertilizer plant. Table 11 concludes that the long-run availability of the system improved from 5.162 to 9.93 %, while Table 12 concludes that the reliability of the system improved from 2.767 to 7.217 % by controlling the failure rate and repair rate of subsystem A₂. Thus, the long-run availability and reliability of the system can be improved significantly by the proper maintenance planning of subsystem A₂. The other subsystems also affect the long-run availability and reliability of the system, but these are lesser effective than subsystem A₂. These findings of this paper are discussed with the management of the plant and these results are found to be highly beneficial for the performance evaluation and to enhance the production and quality of urea.