The efficiency of using CFRP as a strengthening technique for reinforced concrete beams subjected to blast loading

Abstract

Some structures may be subjected to blast loading while in service. This may cause damage or failure to the structural elements. This paper examines the performance of reinforced concrete beams using carbon fiber reinforced polymer (CFRP) when subjected to blast loading. The experimental data including damage and deflection were collected from a previous investigation and numerical analysis was then performed using ABAQUS software. Furthermore, the single degree of freedom (SDOF) model was used to complement the findings from numerical analysis. Following the good correlation between the experimental and numerical data, further analysis was performed on reinforced concrete beams strengthened with carbon fiber-reinforced polymer (CFRP). Using CFRP was found to enhance the load capacity and energy absorption and to reduce the central deflection. In addition, Iso-Damage curves were produced for each beam, thus allowing the assessment of damage to be predicted.

Introduction

The scientific term blast refers to a sudden release of a large amount of energy in a very short time, which makes it distinct from static loading and should be taken into consideration in any design process (Ardila-Giraldo 2010, Temsah et al. 2018a, b). The time history of this load is divided into two regions: the positive phase region, and the negative phase region as shown in Fig. 1. The area of the positive phase region is known as the positive impulse “I⁺”, whereas the area of the negative phase region is known as the negative impulse. Therefore, using mathematical integration, the impulse can be found using Eqs. 1 and 2:

$$I^{ + } = A\int\limits_{{T_{0} }}^{{T_{a} }} {\left( {P\left( t \right) - P_{0} } \right){\text{d}}t} ,$$

(1)

$$I^{ - } = A\int\limits_{{T_{a} }}^{{T_{b} }} {\left( {P_{0} - P\left( t \right)} \right){\text{d}}t.}$$

(2)

Fig. 1

Ideal blast wave (Ardila-Giraldo 2010; Temsah et al. 2018a, b)

Any two blasts can be related to each other using Hopkinson-Cranz Scaling described in Eq. 3. This scale combines the effect of explosive weight and the distance between the explosive and the target. Any two explosions have the same scaling factor will cause the same increase in pressure as mentioned by Magnusson (2007).

$$Z = \frac{R}{{Q^{1/3} }},$$

(3)

where “Z” is the scaled distance, R is the distance from the center of the explosive charge (in meter), and Q is the equivalent TNT mass (Kg).

When blast wave reaches the concrete object, part of it will be reflected and the other part will be transmitted through it. The transmission will cause spalling of concrete at the tension side, and that will cause the object to be damaged (Ramamurthi 2014). Concrete will have stiffer behavior when subjected to blast loads (Malvar and Crawford 1998). Both compressive strength and modulus of elasticity will be increased due to the strain rate effect as shown in Fig. 2. As for steel reinforcement, the yield strength will also increase while the modulus of elasticity remains the same (Temsah et al. 2017a, b). CEB-FIP Model Code (MC90 1993) has derived equations that relates the dynamic properties to static properties for both concrete and steel by the dynamic increasing factor (DIF) as follows:

Fig. 2

Dynamic effect on concrete compressive strength (Temsah et al. 2018a, b)

For concrete compressive strength:

$$\frac{{f_{\text{cd}} }}{{f_{\text{cm}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{c}} }}{{30 \times 10^{ - 6} }}} \right)^{{\left( {\frac{1.016}{{5 + 0.9f_{\text{cm}} }}} \right)}} ,$$

(4)

where “$\grave{\varepsilon}_{\text{c}}$” is the compressive strain rate in concrete, “f_cm” is the static compressive strength of concrete, and “f_cd” is the dynamic compressive strength of concrete.

For concrete tensile strength:

$$\frac{{f_{\text{ctd}} }}{{f_{\text{ctm}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{ct}} }}{{10^{ - 6} }}} \right)^{{\left( {\frac{1}{{1 + 0.8f_{\text{cm}} }}} \right)}} ,$$

(5)

where “$\grave{\varepsilon}_{\text{ct}}$” is the tensile strain rate in concrete, “f_ctm” is the static tensile strength of concrete, and “f_ctd” is the dynamic tensile strength of concrete.

For modulus of elasticity in compression:

$$\frac{{E_{\text{cd}} }}{{E_{\text{cm}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{c}} }}{{30 \times 10^{ - 6} }}} \right)^{0.026} ,$$

(6)

where “E_cm” is the static elastic modulus of concrete in compression and “E_cd” is the dynamic elastic modulus of concrete in compression.

For modulus of elasticity in tension:

$$\frac{{E_{\text{ctd}} }}{{E_{\text{ctm}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{ct}} }}{{3 \times 10^{ - 6} }}} \right)^{0.026} ,$$

(7)

where “E_ctm” is the static elastic modulus of concrete in tension, and “E_ctd” is the dynamic elastic modulus of concrete in tension.

For peak compressive strain:

$$\frac{{\varepsilon_{\text{cd}} }}{{\varepsilon_{\text{cm}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{c}} }}{{30 \times 10^{ - 6} }}} \right)^{0.02} ,$$

(8)

where “$\varepsilon_{\text{cm}}$” is the static compressive strain at maximum compressive stress, and “$\varepsilon_{\text{cd}}$” is the dynamic strain at maximum compressive stress.

For yield strength of steel reinforcement:

$$\frac{{f_{\text{yd}} }}{{f_{\text{y}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{s}} }}{{10^{ - 4} }}} \right)^{{0.074 - 0.04\frac{{f_{\text{y}} }}{414}}} ,$$

(9)

where “$\grave{\varepsilon}_{\text{s}}$” is the strain rate in steel, “$f_{\text{y}}$” is the static yield strength of steel, and “$f_{\text{yd}}$” is the dynamic yield strength of steel.

For the ultimate strength of steel reinforcement:

$$\frac{{f_{\text{ud}} }}{{f_{\text{u}} }} = \left( {\frac{{\grave{\varepsilon}_{\text{s}} }}{{10^{ - 4} }}} \right)^{{0.019 - 0.009\frac{{f_{\text{y}} }}{414}}} ,$$

(10)

where “$f_{\text{u}}$” is the static ultimate strength of steel, and “$f_{\text{ud}}$” is the dynamic ultimate strength of steel.

Equations 4 to 10 were used as input parameters in the numerical analysis

There are many methods to analyze this type of loads. Some of them are related to finite element modeling programs (Hibbitt et al. 2011), and the other related to dynamic analysis theory such as single degree of freedom analysis (SDOF) and multi-degree of freedom analysis (MDOF) (Temsah et al. 2017a, b). This paper will present both finite element and dynamic analysis procedure to verify a blast experiment, and therefore to derive what is called the Iso-damage curve.

The Iso-Damage curve is a curve that relates the applied impulse and pressure to the degree of damage. When an explosion takes place energy will be released, and the facing object will be subjected to a combination of pressure and impulse. This combination of pressure and impulse will cause a specific degree of damage to the object. The static applied load usually have a high impulse compared to pressure since the load is applied slowly (large area under pressure curve), whereas Impulse applied loads have a low impulse compared to pressure since the load is applied in a very short time (small area under pressure curve). All other types of loads that lie between these two categories are called Dynamic applied loads (Temsah et al. 2018a, b). Figure 3 shows the division of Iso-damaged curve. All points that lie above the curve indicates that the explosion’s damage exceeds the value represented by the curve, and all points that lie below the curve will not cause damage more than the degree of damage represented by the curve.

Fig. 3

Iso-Damage curve

Based on the degree of damage many strengthening methods may be used. One of these methods is using CFRP (Carbon Fiber Reinforced Polymers) which has a significant effect on both shear and flexural strengthening of beams and slabs (Jahami et al. 2018). Erki and Meier (1999) and Boyd et al. (2008) examined the use of either CFRP or FRP on damaged reinforced concrete beams. They found that the beams have regained about 95% of their original flexural strength. Moreover, Pham (Pham and Hao 2017) studied the effect of CFRP sheets on RC beams subjected to impact loading. It was found that the strengthening of RC beams with FRP can considerably increase the impact resistance in both flexure and shear. However, the main failure occurred between the RC face and CFRP sheet through delamination.

As can be noticed, there has been extensive research on the use of CFRP in reinforced concrete beams for strengthening against blast loading (Urgessa et al. 2005); (Mosalam and Mosallam 2001); (De Lorenzis and La Tegola 2005). However, there is a little work for determining the required explosive mass to cause a specific degree of damage for RC beams strengthened with CFRP.

Aim and objectives

The aim of this research is to derive numerically, using the ABAQUS software, an Iso-damage curve for a reinforced concrete beam subjected to blast loading with and without CFRP sheets. In addition, the exact mass of TNT to cause a specific degree of damage will be determined for a known standoff distance.

Data collection

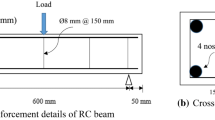
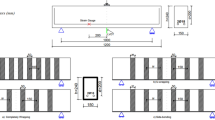
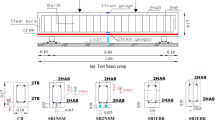
The experimental results obtained by Zhang et al. (2013) at National University of Defense Technology were used as input data in the numerical analysis. The experiments consisted of reinforced concrete beams with varying dimensions; 850mm × 75 mm × 75mm, 1100 mm × 100mm × 100mm and 1350mm × 125 mm × 125mm. However, beams with dimensions of 1100 mm × 100mm × 100mm were used in the numerical analysis. The diameter of all reinforcement (tensile, compressive and shear) was 6 mm. The spacing between links was 60 mm. Four different weights of explosive and one standoff distance were considered. The blast loading used in the experimental program was placed over the center of the reinforced concrete (RC) beam and an electronic device was used for the detonation. A steel frame was used to support the reinforced concrete beam. The steel frame used for supporting the reinforced concrete beams and other experimental details for measuring the central deflection is shown in Fig. 4. The dimensions of the beams used in the analysis and testing details are presented in Table 1. The concrete had a strength of 40 MPa. The yield and ultimate stresses of the reinforcing steel were 395 MPa and 501 MPa, respectively.

Fig. 4

Experimental setup (Zhang et al. 2013)

Table 1 Number and dimensions of beams

Numerical modeling

As indicated earlier that the data used in the computer simulation were those of Zhang’s experiment (2013). The software used for this purpose was “ABAQUS CAE”, which is a powerful volumetric finite element program. The concrete body and steel supports were modeled as solid element (C3D8R) whereas steel rebars were modeled as wire elements (T3D2), (Hibbitt et al. 2011) as shown in Figs. 5 and 6. As for blast load, ABAQUS built-in model “CONWEP” was used to simulate the explosion, and that can be achieved easily by assigning an equivalent TNT explosive to a reference point set at a distance from the target.

Fig. 5

Beam and cylinder modeling

Fig. 6

Flexural and shear reinforcement modeling

Mechanical properties of concrete were modeled using the built-in Concrete Damage Plasticity method (CDP). This method is very important when studying concrete under dynamic loads. It was derived by Lublinear et al. (1989) and developed by Lee and Fenves (1998). It represents the nonlinear behavior of concrete using different input parameters such as inelastic strain, cracking strain, stiffness degradation and recovery, and other parameters. The behavior of concrete in tension and compression according to the CDP method in ABAQUS is illustrated in Figs. 7 and 8, respectively (Hibbitt et al. 2011). The uniaxial behaviour of concrete in compression is defined as a stress-inelastic strain curve, while in tension it is defined as a stress-cracking strain curve as shown:

$$\varepsilon^{\text{in}} = \varepsilon c - \frac{{\sigma_{\text{c}} }}{{E_{0} }},$$

(11)

$$\varepsilon^{\text{ck}} = \varepsilon t - \frac{\sigma t}{{E_{0} }},$$

(12)

where “εⁱⁿ” is the inelastic strain in compression, “E₀” is the initial modulus of elasticity, “σ_c” is the compressive stress in concrete, “ε^ck” is the cracking strain in tension, and “σ_t” is the tensile stress in concrete. The inelastic and crack strain were then converted into a plastic strain using the damage parameters as follows:

$$\varepsilon^{\text{pl}} = \varepsilon^{\text{in}} - \left( {\frac{{d_{\text{c}} }}{{1 - d_{\text{c}} }}} \right)\left( {\frac{{\sigma_{\text{c}} }}{{E_{0} }}} \right),$$

(13)

$$\varepsilon^{\text{pl}} = \varepsilon^{\text{ck}} - \left( {\frac{{d_{\text{t}} }}{{1 - d_{\text{t}} }}} \right)\left( {\frac{{\sigma_{\text{t}} }}{{E_{0} }}} \right),$$

(14)

where “ε^pl” is the plastic strain at compression and at tension, “d_c” is the concrete compressive damage (d_c = 0 for undamaged concrete and 1 for fully damaged concrete), “d_t” is the concrete tensile damage (d_t = 0 for undamaged concrete and 1 for fully damaged concrete). The stiffness degradation of concrete is defined as:

$$d_{\text{c}} = 1 - \frac{{\sigma_{\text{c}} .E_{0}^{ - 1} }}{{\sigma_{\text{c}} \cdot E_{0}^{ - 1} + \varepsilon^{\text{in}} \left( {1 - b_{\text{c}} } \right)}},$$

(15)

$$d_{\text{t}} = 1 - \frac{{\sigma_{\text{t}} \cdot E_{0}^{ - 1} }}{{\sigma_{\text{t}} \cdot E_{0}^{ - 1} + \varepsilon_{\text{t}}^{\text{pl}} \left( {1 - b_{\text{t}} } \right)}}.$$

(16)

Fig. 7

Uniaxial behaviour of concrete under tension

Fig. 8

Uniaxial behaviour of concrete under compression

The factors “b_c” and “b_t” relate the inelastic and plastic strains. They can be determined using the results of curve fitting of cyclic tests, and have approximate default values of 0.7.

In addition, the effect of high strain ratio due to impact on concrete properties was included using Eqs. 4 to 10 (Al Rawi et al. 2018; Elani et al. 2018). Concrete mechanical properties for both static and dynamic load conditions are shown in Table 2.

Table 2 Mechanical properties of concrete

For reinforcing steel, they can be modeled using several methods. For this simulation, the elastoplastic behavior of reinforcing steel was considered and a perfect bond was assumed between concrete and steel. However, a coefficient of friction of 0.7 was considered between steel supports and the concrete body. Table 3 shows the mechanical properties for steel rebars.

Table 3 Mechanical Properties of Steel reinforcement

Model calibration

Both finite element analysis (ABAQUS CAE) and SDOF analysis were calibrated and verified to match the experimental work done by (Zhang et al. 2013). Table 4 summarizes the deflection results for each analysis. As can be seen, both SDOF analysis and Finite element modeling successfully calibrated the experiment. The average error in both calibrations was 12.4% for SDOF and 6.44% for the finite element. The increasing error in the SDOF method is due to the approximation used in the analysis. These include; the material properties, DIF (Dynamic Increase Factor), and Impact load-time history. Figure 9 shows the load–deflection curves due to finite element modeling held by ABAQUS. As the intensity of the blast increases, the deflection increases.

Table 4 Mid-span deflection for experimental, SDOF, and finite element modeling analysis

Fig. 9

Load–deflection curves for all beams

Another parameter was verified to calibrate the model. This parameter is the width of both tensile and compressive damage zone. Table 5 shows the damaged zone width for both experimental and finite element modeling. The width and percentages of the damage zones reflect the validity of the finite element model as for the deflection results (Table 4). Figures 10, 11, 12, and 13 show the effect of blast load on the extent of damage of the RC beams (B2-2 and B2-4), both at the top (compression) and at the bottom (tension) face. In both beams (B2-2 and B2-4), the area of the damaged zone in compression is larger than that of the tensile zone.

Table 5 Top and bottom damage

Fig. 10

Compression damage (B2-2)

Fig. 11

Tensile damage (B2-2)

Fig. 12

Compression damage (B2-4)

Fig. 13

Tensile Damage (B2-4)

Iso-Damage curves for all samples are shown in Fig. 14. Each curve represents a specific degree of damage in terms of mid-span deflection. The deflection values at mid-span; 9 mm, 25 mm, 35 mm, and 40 mm for Beams B2-1, B2-2, B2-3, and B2-4, respectively. The Iso-Damage curve is derived by employing several numerical analysis trials. Each analysis has different combinations of explosive mass and standoff distance for the beams used in the experimental investigation. A point on each curve represents a combination of explosive mass and standoff distance that will cause the same mid-span deflection. If a point lies above the curve, the deflection will be greater. Less deflection will be expected if the point is located below the curve.

Fig. 14

Iso-Damage curves for beam samples

Strengthening beams using CFRP

Further analysis on beam B2-2 where four cases were considered. The first case was the reference and no strengthening was used. In the remaining cases (case 2–4), one layer, two layers and four layers of CFRP were used, respectively, in the simulation at the bottom of the beam. Each layer has a thickness of 1 mm. The mechanical properties of CFRP are: The elasticity modulus, tensile strength, and maximum strain were 74.7 GPa, 933 MPa, and 1.25%, respectively. Figures 15, 16, 17 and 18 shows the load–deflection curve for each case. It can be noticed that using CFRP reduces deflection due to the explosion. However, by increasing the number of layers of CFRP, the rate of reduction in deflection decreased. This is likely to be due to the bond strength capacity between the CFRP and the concrete face. If this bond strength is exceeded, the number of layers would not have any significant influence.

Fig. 15

B2-2 with no CFRP

Fig. 16

B2-2 with one layer of CFRP

Fig. 17

B2-2 with two layers of CFRP

Fig. 18

B2-2 with four layers of CFRP

Figure 19 plots the energy dissipated against time for the beams with various layers of CFRP. It can be noticed that as the number of layers increases, the energy dissipation increases. However, and similar to the deflection trend, the more the number of layers, the less the rate increase in dissipated energy as shown in Fig. 20.

Fig. 19

Dissipated internal energy for each case

Fig. 20

Dissipated energy at different times

Figure 21a, b show the tensile damage, whereas Fig. 21c, d show the compressive damage in beam B2-2 without CFRP and with four layers of CFRP. It can be noticed that the beam with four layers of CFRP had less red areas indicating less tensile damage. The CFRP laminates may absorb the shock from the explosion (Jahami et al. 2018). However, the compression damage was similar for beams with and without CFRP.

Fig. 21

Concrete damage for B2-2. a No CFRP (tensile damage). b Four layers of CFRP (tensile damage). c No CFRP (compressive damage) d Four layers of CFRP (compressive damage)

Iso-Damage curves were plotted beam B2-2 with and without CFRP as shown in Fig. 22. A different set of trials were carried out to derive these curves. As can be seen, using one layer of CFRP will increase the required combination of pressure and impulse to cause the same damage as the case without any strengthening. Hence more explosion charge can be detonated and a closer standoff distance can be achieved for the same damage level. However, Increasing CFRP laminate thickness beyond a certain number of layers is not necessarily efficient in enhancing the capacity for beams subjected to blast loading. A closer view for Iso-damage curves for 25 mm deflection in Fig. 23 shows that the 4-layer curve is too close to the 2-layer curve, which indicates that the governing failure mode is likely to be due to the bond between concrete and CFRP surfaces.

Fig. 22

Iso-Damage curve for B2-2 with and without strengthening

Fig. 23

Closed view for Iso-Damage curve for B2-2

Further analysis was conducted to examine the effect of CFRP in terms of explosion weight. To achieve this, the values of pressure from the Iso-Damage curves at the same impulse value were plotted for all cases as can be seen in Fig. 24. As can be observed, the pressure required to cause the same level of damage was increased by increasing the number of layers. For example, an explosion with an impulse value of 300 Pa.s, a pressure of 195,000 Pa is required for the beam strengthened with 4 layers of CFRP to cause the same damage compared with 130,000 Pa for the beam without CFRP.

Fig. 24

Pressure values at the same Impulse

Several numerical simulations were conducted to find the value of TNT weight that causes the same degree of damage for B2-2 sample without CFRP. This was achieved using a number of TNT masses detonated from the same distance (0.4 m) until reaching the required damage (a deflection of 25 mm). Figure 25 illustrates the TNT mass required for each explosion Impulse value. For example and for an impulse value of 500 Pa.s, the required TNT mass to cause the same damage was 0.45, 0.85, 0.92 and 0.94 kg for beam B2-2 strengthened with 0 (i.e. No CFRP), 1, 2 and 4 layers of CFRP, respectively.

Fig. 25

TNT mass required to cause the same damage

Referring to Fig. 25, it can be noted that using CFRP increased the required explosive mass needed to cause the same damage to the unstrengthened sample (B2-2). The percentage increase varied between 10 and 50%.

Conclusion

• The prediction of the response of blast loaded reinforced concrete beams using a finite element program such as ABAQUS is possible. The built-in CONWEP model that simulates the blast load pressure is an accurate tool that can be used in similar simulations to find the blast response for structural elements with deferent boundary conditions.

• The built-in concrete damage plasticity model (CDP) was simulated successfully the nonlinear behavior of concrete under impact loading. It requires taking into consideration the strain rate effect on the concrete damage plasticity parameters to get an acceptable response with minimal error.

• It is possible to form the Iso-Damage curve for any structural elements using Finite Element Program such as ABAQUS. This can be accomplished using several combinations of TNT mass and standoff distance to obtain the equivalent pressure and impulse values.

• Using CFRP reduced the extent of damage of the reinforced concrete beams when subjected to blast loads. As the number of layers of CFRP increased as demonstrated by the mid-span deflection. The mid-span deflection for beams with 4 layers of CFRP is 30% lower than that of a beam without CFRP. However, using more than 2 layers does not cause a further decrease in deflection.

• A reinforced concrete beam is able to resist higher blast load in the presences of CFRP. Strengthening the beam with four layers with CFRP can increase the TNT mass by 50% to cause the same damage compared with a beam without CFRP.

• Using CFRP sheets in reinforced concrete beams increased the absorbed energy of the beam. Higher absorption energy is associated with a reduced number and propagation of cracks.