Exact finite element formulation in generalized beam theory

Abstract

This paper presents the formulation of exact stiffness matrices applied in linear generalized beam theory (GBT) under constant and/or linear loading distribution in the longitudinal direction. Also, the assortment of the correct exact stiffness matrix and the corresponding shape function are presented based on main transversal deformation mode, which can be divided into: (1) dominant distortion mode; (2) dominant torsion mode; (3) and critical distortion–torsion mode. Special attention is given to the hyperbolic–trigonometric shape functions, which are organized in a system of vector in function of longitudinal direction and a coefficient matrix obtained from the completeness requirement. This approach has the benefit of compacting the terms of the stiffness matrix and systematizing the boundary conditions of an element by applying the completeness coefficient matrix as a transformation matrix. As a result, in linear analysis, a single element can represent the stress and displacement fields. Moreover, due to the higher-order continuous derivatives properties of hyperbolic–trigonometric shape functions, the generalized internal shear is obtained without the typical discontinuity of Hermitian shape functions. A full and detailed example, applied in a thin-walled circular hollow cross section, provides not only an illustration of the presented approach, but also a quick introduction point in GBT.

Introduction

Generalized beam theory, GBT, is a numerical approach, which was initially developed to describe open thin-walled beams by Richard Schardt in Darmstadt, Germany. This approach is applicable to linear analysis (Schardt 1989), but it has been further extended to geometric non-linear analysis (Schardt 1994). This method splits the displacement and stress fields of a spatially dependent beam function in the cross section via separation of variables. As a result, this approach presents astonishing numerical performance and a clear representation of the displacement and stress fields as a linear combination of the generalized cross-sectional proprieties and internal forces.

Separation of variables in GBT consists of two steps. The first step requires a cross-sectional analysis by solving a quadratic eigenvalue problem, which is quite elaborate. Consequently, this step has been widely studied and relevant progress has been achieved in many cross sections, such as arbitrary branched opened (Dinis et al. 2006) and elliptical (Silvestre 2008) cross sections. The performance and robustness of the numerical approach have also been studied (Jönsson and Andreassen 2011; Andreassen and Jönsson 2012).

The second step involves analyzing the beam along the longitudinal direction by solving a system of uncoupled ordinary differential equations. This second step is the main focus of this work.

In the original works of Richard Schardt and his co-workers, the ordinary differential equations were evaluated by the finite difference method. Although this method has a clear and direct numerical solution, it has been replaced by the finite element method (FEM) in structural analysis, owing to the well-known versatility of this method (Silvestre and Camotim 2003a).

The first application of FEM in GBT was performed by Davies (1986), who proposed the use of an exact element. However, the formulation presented contains some controversial points. First, the stiffness components of transverse distortion are not included in the complete stiffness matrix. Second, the shape function used in the formulation is based on the homogeneous solution, which is a linearly independent function of most usual load functions, such as a constant loading distribution.

Silvestre and Camotim (2003a) developed a finite element based on Hermitian shape functions. This method has been extensively applied in many studies and analyses, such as Silvestre and Camotim (2003b), Gonçalves et al. (2010), Correia et al. (2011), and Abambres et al. (2013, 2014). Although this type of element has good convergence and allows easy implementation of the stiffness matrix, it does not reach an exact solution and it also requires longitudinal discretization. Moreover, the generalized internal force obtained from Hermitian shape functions presented a coarse result due to the higher-order derivatives that are necessary to achieve it. These issues affect the non-linear analysis, i.e., the initial stress stiffness matrix (Camotim et al. 2011).

As an alternative to overcome these coarse results in higher-order problems, Duan et al. (2016) presents the formulation of a B-splines-based GBT, which provides continuity between two adjacent elements. However, this alternative still requires longitudinal discretization.

This letter presents a review of the exact stiffness matrix formulation of GBT and compares the pros and cons between this formulation and the one based on Hermitian shape functions.

Shape function assortment and the transverse deformation mode classification

The development of shape functions that describe the exact displacement field in GBT is initially based on the analytical solution to the following ordinary differential equation:

$$\begin{aligned} ECV''''(x)-(GD-2\mu K D_\mu )V''(x)+BV(x) = q(x). \end{aligned}$$

(1)

V(x) is a displacement amplification function in the longitudinal direction x, E is Youngs modulus, $\mu$ is Poisson’s ratio, C is the generalized moment of inertia, G is the shear modulus, D is the generalized longitudinal rotation inertia, D is the generalized inertia due to the Poisson effect, and B is the transverse bending stiffness. For convenience, one can consider the following effective generalized longitudinal rotation stiffness:

$$\begin{aligned} \overline{GD} = GD-2\mu K D_\mu . \end{aligned}$$

(2)

The homogeneous part in Eq. (1) is

$$\begin{aligned} ECV''''(x)-\overline{GD}V''(x)+BV(x) = 0 \end{aligned}$$

(3)

and has the characteristic equation:

$$\begin{aligned} ECm^4-GDm^2+B = 0 \end{aligned}$$

(4)

with the following possible roots:

$$\begin{aligned} m_1,_2,_3,_4 = \pm \sqrt{\frac{\overline{GD}}{2EC} \pm \sqrt{\left( \frac{\overline{GD}}{2EC}\right) ^2-\frac{B}{EC}}}. \end{aligned}$$

(5)

The internal square root can classify not only the mathematical type of numerical root, but also the main stiffness component in a transverse deformation mode of the cross section (i.e., torsion or distortion). Therefore, one can derive the following cases:

• Case A: dominant distortion mode:

${ \left( \frac{\overline{GD}}{2EC}\right) ^2<\frac{B}{EC} }$ i.e., ${ \overline{GD}<2\sqrt{BEC}}$.

Deformation modes, in this case, are the main contribution to total transverse stiffness due to transverse bending of each wall in the cross section. This case is the main focus of the present work, owing to the fact that it is the most usual case in GBT and it was studied in Schardt’s work (1989). With two real and one complex conjugate roots, the solution of the differential homogeneous equation is

$$\begin{aligned} V(x)&=K_1\cosh (\alpha x)\cos (\beta x)+K_2\cosh (\alpha x)\sin (\beta x)\nonumber \\&\quad +K_3\sinh (\alpha x)\sin (\beta x)+K_4\sinh (\alpha x) \cos (\beta x), \end{aligned}$$

(6)

where ${K_1}$, ${K_2}$, ${K_3}$, and ${K_4}$ are constants found from the boundary conditions. In addition, we have the following:

$$\begin{aligned} \alpha = \sqrt{\sqrt{\frac{B}{4EC}}+\frac{\overline{GD}}{4EC}} \end{aligned}$$

(7)

$$\begin{aligned} \beta = \sqrt{\sqrt{\frac{B}{4EC}}-\frac{\overline{GD}}{4EC}}. \end{aligned}$$

(8)

• Case B: dominant torsion mode:

${ \left( \frac{\overline{GD}}{2EC}\right) ^2>\frac{B}{EC} }$ i.e.${ \overline{GD}>2\sqrt{BEC}}$.

In this case, torsion of each wall in the cross section is the main contributor to the total transverse stiffness for deformation modes. This case occurs specially when the extremity walls are much thicker than the internal walls of an opened cross section. With four real roots, the solution of the differential homogeneous equation is:

$$\begin{aligned} V(x)&=K_1\cosh (\zeta x)\cosh (\eta x)+K_2\cosh (\zeta x)\sinh (\eta x)\nonumber \\&\quad +K_3\sinh (\zeta x)\sinh (\eta x)+K_4\sinh (\zeta x) \cosh (\eta x), \end{aligned}$$

(9)

where:

$$\begin{aligned} \zeta = \sqrt{\frac{\overline{GD}}{2EC} +\sqrt{\left( \frac{\overline{GD}}{2EC}\right) ^2-\frac{B}{EC}}}, \end{aligned}$$

(10)

$$\begin{aligned} \eta = \sqrt{\frac{\overline{GD}}{2EC} -\sqrt{\left( \frac{\overline{GD}}{2EC}\right) ^2-\frac{B}{EC}}}. \end{aligned}$$

(11)

• Case C: torsion and distortion mode:

${ \left( \frac{\overline{GD}}{2EC}\right) ^2=\frac{B}{EC} }$ i.e., ${ \overline{GD}=2\sqrt{BEC}}$.

In this particular case, torsion and transverse bending of each wall in the cross section have the same contribution in the total transverse stiffness for deformation modes. This case is the border between the two previously presented cases. With two pairs of identical real roots, the solution of the differential homogeneous equation is:

$$\begin{aligned} V(x)&=K_1 x\cosh (\gamma x)+K_2 x\sinh (\gamma x)+K_3\cosh (\gamma x)\nonumber \\&\quad +K_4\sinh (\gamma x) \end{aligned}$$

(12)

with: $\gamma = \sqrt{\frac{\overline{GD}}{2EC}}.$

Variational formulation in generalized beam theory

Before developing the shape functions in FEM, a brief review of the variational formulation for GBT in the longitudinal direction is presented here. Following the equilibrium principle, the particular solution of Eq. (1) is found in the minimal energy system, together with the boundary conditions of the generalized beam. It can be obtained from the minimization of the total energy functional that

$$\begin{aligned} \Pi = U_{\text {int}} - V_{\text {ext}} \end{aligned}$$

(13)

$$\begin{aligned} \delta \Pi = \delta U_{\text {int}} -\delta V_{\text {ext}} = 0, \end{aligned}$$

(14)

where $\Pi$ is the total energy, $U_{\text {int}}$ the internal strain energy, and $V_{\text {ext}}$ the external load potential energy. Below, each term is developed according to GBT.

Internal strain energy according to GBT

Following the assumptions of GBT in an arbitrary beam cross section, the variation of the internal strain energy can be described as a combination of four main components:

• Longitudinal strain energy (which considers the effect of membrane stiffness ${}^iC^m$ and plate stiffness ${}^iC^p$).

• Shear strain energy, which considers only the plate behavior.

• Transverse strain energy due to transverse bending of the plate.

• Strain energy due to the Poisson effect in the plate’s constitutive material law.

Therefore, the total variation of the internal stress energy is obtained by the sum of these respective terms, as follows:

$$\begin{aligned} \delta U_{\text {int}}&=\int \limits _L \!\! E{}^iC{}^iV''(x)\delta {}^iV''(x)+ G\,{}^iD\,{}^iV'(x)\delta \,{}^iV'(x)\nonumber \\&\quad +{}^iB\,{}^iV(x)\delta \,{}^iV(x) +\mu K\,{}^iD_{\mu }\left( \,{}^iV\left( x\right) \delta \,{}^iV''\left( x\right) \right. \nonumber \\&\quad +\left. \delta \,{}^iV\left( x\right) \,{}^iV''\left( x\right) \right) {\text {d}}x. \end{aligned}$$

(15)

External load potential energy according to GBT

Following the same principle of the internal energy, the external load potential energy can be expressed by a summation of the orthogonal modes:

$$\begin{aligned} V_{\text {ext}}&= \sum \limits _{i=1}^n \int \limits _L \,{}^iq_x(x)\,{}^iu{}^iV'(x) + \,{}^iq_s(x) \,{}^iv{}^iV(x)\nonumber \\&\quad +{}^iq_v(x)\,{}^iw{}^iV(x) \, {\text {d}}x + \,{}^iQw_i\,{}^iV_i + \,{}^iQw_f\,{}^iV_f\nonumber \\&\quad +{}^iQx_i\,{}^iV'_i + \,{}^iQx_f\,{}^iV'_f ). \end{aligned}$$

(16)

Here, the terms Qx and Qw are the concentrated generalized forces that can be applied at the initial or final beam nodes (the subscripts i and f represent these two points). Obtaining the variation of this functional in terms of amplification functions ${}^iV$ yields the following:

$$\begin{aligned} \delta V_{\text {ext}}&= \int \limits _L \,{}^iq_x(x)\,{}^iu \delta {}^iV'(x)+ \,{}^iq_s(x) \,{}^iv\delta {}^iV(x)\nonumber \\&\quad +{}^iq_v(x)\,{}^iw\delta {}^iV(x) \, {\text {d}}x + \,{}^iQw_i\,\delta {}^iV_i + \,{}^iQw_f\,\delta {}^iV_f\nonumber \\&\quad +{}^iQx_i\,\delta {}^iV'_i + \,{}^iQx_f\,\delta {}^iV'_f. \end{aligned}$$

(17)

Equilibrium by Hamilton’s principle

Introducing variations of internal strain energy Eq. (15) and external potential energy Eq. (17) into Hamilton’s principle presented in Eq. (14), one can obtain:

$$\begin{aligned} 0&= \int \limits _L E\,{}^iC\,{}^iV''(x)\delta \,{}^iV''(x) + G\,{}^iD\,{}^iV'(x)\delta \,{}^iV'(x) \nonumber \\&\quad +{}^iB\,{}^iV(x)\delta \,{}^iV(x)+\mu K\,{}^iD_{\mu }\left( \,{}^iV\left( x\right) \delta \,{}^iV''\left( x\right) \right. \nonumber \\&\quad +\left. \delta \,{}^iV\left( x\right) \,{}^iV''\left( x\right) \right) -\,{}^iq_x(x)\,{}^iu \delta {}^iV'(x) \nonumber \\&\quad -\,{}^iq_s(x) \,{}^iv\delta {}^iV(x)- \,{}^iq_v(x)\,{}^iw\delta {}^iV(x) \, {\text {d}}x - \,{}^iQw_i\,\delta {}^iV_i \nonumber \\&\quad -{}^iQw_f\,\delta {}^iV_f- \,{}^iQx_i\,\delta {}^iV'_i - \,{}^iQx_f\,\delta {}^iV'_f. \end{aligned}$$

(18)

Integrating the terms involving $\delta \,{}^iV''(x)$ by parts twice, and integrating the second term in the above integral by parts once, we find:

$$\begin{aligned}&\int \limits _L \left( E\,{}^iC\,{}^iV''(x)+\mu K\,{}^iD_{\mu } \,{}^iV\left( x\right) \right) \delta \,{}^iV''(x)\, {\text {d}}x\nonumber \\&\quad =\int \limits _L \left( E\,{}^iC\,{}^iV''''(x)+\mu K\,{}^iD_{\mu } \,{}^iV''\left( x\right) \right) \delta \,{}^iV(x) \, {\text {d}}x\nonumber \\&\qquad +\left[ \left( E\,{}^iC\,{}^iV''(x)+\mu K\,{}^iD_{\mu } \,{}^iV\left( x\right) \right) \delta \,{}^iV'(x)\right] _i^f \nonumber \\&\qquad -\left[ \left( E\,{}^iC\,{}^iV'''(x)+\mu K\,{}^iD_{\mu } \,{}^iV'\left( x\right) \right) \delta \,{}^iV(x)\right] _i^f, \end{aligned}$$

(19)

$$\begin{aligned} \int \limits _L G\,{}^iD\,{}^iV'(x)\delta \,{}^iV'(x) {\text {d}}x&= [G\,{}^iD\,{}^iV'(x)\delta \,{}^iV(x)]_i^f\nonumber \\&\quad -\int \limits _L G\,{}^iD\,{}^iV''(x)\delta \,{}^iV(x) {\text {d}}x. \end{aligned}$$

(20)

Replacing these results in Eq. (18) with the expression in Eq. (2), we find:

$$\begin{aligned} 0&= \int \limits _L \left( E\,{}^iC\,{}^iV''''(x) -\overline{G\,{}^iD\,{}^i}V''(x) +{}^iB\,{}^iV(x)\right. \nonumber \\&\quad -\left. \,{}^iq_x(x)\,{}^iu - \,{}^iq_s(x) \,{}^iv - \,{}^iq_v(x)\,{}^iw\right) \delta {}^iV(x) \, {\text {d}}x \nonumber \\&\quad +\left[ \left( E\,{}^iC\,{}^iV''(x)+\mu K\,{}^iD_{\mu } \,{}^iV\left( x\right) \right) \delta \,{}^iV'(x)\right] _i^f\nonumber \\&\quad +\left[ \left( \left( G\,{}^iD-\mu K\,{}^iD_{\mu }\right) \,{}^iV'(x)-E\,{}^iC\,{}^iV'''(x)\right) \delta \,{}^iV(x)\right] _i^f\nonumber \\&\quad -{}^iQw_i\,\delta {}^iV_i - \,{}^iQw_f\,\delta {}^iV_f- \,{}^iQx_i\,\delta {}^iV'_i - \,{}^iQx_f\,\delta {}^iV'_f. \end{aligned}$$

(21)

Here, the equilibrium and the boundary conditions stand out. Taking into account that the functional Eq. (21) must vanish for any arbitrary longitudinal amplification functions $\delta$V(x), the parentheses terms in the integral must be zero, which gives the equilibrium condition in Eq. (1), with $q(x)=\,{}^iq_x(x)\,{}^iu - \,{}^iq_s(x) \,{}^iv - \,{}^iq_v(x)\,{}^iw$. In the same way, the boundary conditions are found in the remaining terms:

$$\begin{aligned} \left[ \left( \left( G\,{}^iD-\mu K\,{}^iD_{\mu }\right) \,{}^iV'(x)-E\,{}^iC\,{}^iV'''(x)- \,{}^iQw_i\right) \delta \,{}^iV(x)\right] _i=0, \end{aligned}$$

(22)

$$\begin{aligned} \left[ \left( \left( G\,{}^iD-\mu K\,{}^iD_{\mu }\right) \,{}^iV'(x)-E\,{}^iC\,{}^iV'''(x)- \,{}^iQw_f\right) \delta \,{}^iV(x)\right] _f=0, \end{aligned}$$

(23)

$$\begin{aligned} \left[ \left( E\,{}^iC\,{}^iV''(x)\!+\!\mu K\,{}^iD_{\mu }\,{}^iV(x)- {}^iQx_i\right) \delta \,{}^iV'(x)\right] _i = 0, \end{aligned}$$

(24)

$$\begin{aligned} \left[ \left( E{}^iC\,{}^iV''(x)\!+\!\mu K\,{}^iD_{\mu }{}^iV(x)- {}^iQx_f\right) \delta \,{}^iV'(x)\right] _f\! = 0. \end{aligned}$$

(25)

The function describing longitudinal amplification V(x) is obtained via superposition of the interpolation functions, which are presented below.

Shape functions based on homogeneous and inhomogeneous solution of GBT ordinary differential equation

The formulation of a GBT element based on homogeneous solutions is a particular case of the inhomogeneous solution. In fact, the equilibrium part of the variational formulation given by Eq. (18) in the homogeneous case is reduced into the form:

$$\begin{aligned} 0&= \int \limits _L E\,{}^iC\,{}^iV''(x)\delta \,{}^iV''(x) + G\,{}^iD\,{}^iV'(x)\delta \,{}^iV'(x) \nonumber \\&\quad +{}^iB\,{}^iV(x)\delta \,{}^iV(x)+\mu K\,{}^iD_{\mu }\left( \,{}^iV\left( x\right) \delta \,{}^iV''\left( x\right) \right. \nonumber \\&\quad +\left. \delta \,{}^iV\left( x\right) \,{}^iV''\left( x\right) \right) {\text {d}}x - \,{}^iQw_i\,\delta {}^iV_i - \,{}^iQw_f\,\delta {}^iV_f\nonumber \\&\quad -\,{}^iQx_i\,\delta {}^iV'_i - \,{}^iQx_f\,\delta {}^iV'_f. \end{aligned}$$

(26)

Because the homogeneous solution can only be applied under nodal loading cases, only the formulation related to the inhomogeneous solution is presented here.

In inhomogeneous differential equations, the general solution is a combination between the homogeneous and a particular solution, which represents an external load function. In the most common structural analysis, the external load functions are constants or linear functions, which are linearly independent from the homogeneous solutions of cases A, B and C. Therefore, the function of the exact solution of inhomogeneous equation needs six terms, four from the boundary conditions: $K_1$, $K_2$, $K_3$, and $K_4$, presented in Eqs. (6), (9) and (12) , and two extra terms due to loading distribution $K_5x + k_6$, as shown below:

$$\begin{aligned} V(x)&=K_1\cosh (\alpha x)\cos (\beta x)+K_2\cosh (\alpha x)\sin (\beta x)\nonumber \\&\quad +K_3\!\sinh (\!\alpha x)\!\sin (\!\beta x)\!+\!K_4\!\sinh (\!\alpha x) \!\cos (\beta x) \!+\!K_5x+\!K_6, \end{aligned}$$

(27)

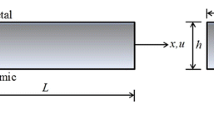
which leads to three nodes for each element, with two degrees of freedom per node. Further, for convenience of symmetric and anti-symmetric properties of trigonometric function, the initial node is chosen as $x=-\frac{L}{2}$ and the final node as $x=\frac{L}{2}$, as shown in Fig. 1.

Fig. 1

Element for inhomogeneous solution with six degrees of freedom

All element formulations presented here are based on this element with an extra node. Nevertheless, one can note that this extra node can be avoided by a static contraction as presented.

Inhomogeneous solution for case A with clamped–clamped boundary conditions

Starting with the shape functions of the dominant distortion mode (case A), in clamped–clamped¹ boundary conditions, it is necessary to satisfy the completeness principle: each interpolation function corresponds to a nodal displacement (transverse or longitudinal). Moreover, each interpolation function must have a unitary value for its respective nodal displacement and vanish for other displacements and nodes  (Soriano 2003). For instance, the first shape function, ${\text {Sh}}_{\text {Hacc1}}$, which interpolates the initial generalized displacement, is based on Eq. (27):

$$\begin{aligned} {\text {Sh}}_{\text {Hacc1}}&= S_{11}\cosh (\alpha x)\cos (\beta x)+S_{21}\cosh (\alpha x)\sin (\beta x) \nonumber \\&\quad +S_{31}\sinh (\alpha x)\!\sin (\beta x)+\!S_{41}\sinh (\alpha x) \cos (\beta x)+S_{51}x+\!S_{61}. \end{aligned}$$

(28)

$S_{ij}$ is the $i{\text {nd}}$ constant value of shape function j. The constants above must satisfy the following conditions:

$$\begin{aligned} {\text {Sh}}_{\text {Hacc1}} \left( x=-\frac{L}{2}\right)&= 1\, \therefore \,S_{11}\cosh \left( -\frac{\alpha L}{2}\right) \cos \left( -\frac{\beta L}{2}\right) \nonumber \\&\quad +S_{21}\cosh \left( -\frac{\alpha L}{2}\right) \sin \left( -\frac{\beta L}{2}\right) + S_{31}\sinh \left( \frac{-\alpha L}{2}\right) \sin \left( \frac{-\beta L}{2}\right) \nonumber \\&\quad + S_{41}\sinh \left( -\frac{\alpha L}{2}\right) \cos \left( -\frac{\beta L}{2}\right) -S_{51}\frac{L}{2}+S_{61}=1, \end{aligned}$$

(29)

$$\begin{aligned}&{\text {Sh}}_{\text {Hacc1}}'\left( x=-\frac{L}{2}\right) = 0 \, \therefore\, \nonumber \\&S_{11}\left( \alpha \sinh \left( -\frac{\alpha L}{2}\right) \cos \left( -\frac{\beta L}{2}\right) -\beta \cosh \left( -\frac{\alpha L}{2}\right) \sin \left( -\frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{21}\left( \alpha \sinh \left( -\frac{\alpha L}{2}\right) \sin \left( -\frac{\beta L}{2}\right) +\beta \cosh \left( -\frac{\alpha L}{2}\right) \cos \left( -\frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{31}\left( \alpha \cosh \left( -\frac{\alpha L}{2}\right) \sin \left( -\frac{\beta L}{2}\right) +\beta \sinh \left( -\frac{\alpha L}{2}\right) \cos \left( -\frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{41}\left( \alpha \cosh \left( -\frac{\alpha L}{2}\right) \cos \left( -\frac{\beta L}{2}\right) -\beta \sinh \left( -\frac{\alpha L}{2}\right) \sin \left( -\frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{51} = 0, \end{aligned}$$

(30)

$$\begin{aligned}&{\text {Sh}}_{\text {Hacc1}}\left( x=\frac{L}{2}\right) = 0 \,\, \therefore\, \nonumber \\&S_{11}\cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) +S_{21}\cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \nonumber \\&\quad +S_{31}\sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) +S_{41}\sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \nonumber \\&\quad +S_{51}\frac{L}{2}+S_{61} = 0, \end{aligned}$$

(31)

$$\begin{aligned}&{\text {Sh}}_{\text {Hacc1}}'\left( x=\frac{L}{2}\right) = 0 \, \, \therefore\, \nonumber \\&S_{11}\left( \alpha \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) -\beta \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{21}\left( \alpha \sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) +\beta \cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{31}\left( \alpha \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) +\beta \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{41}\left( \alpha \cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) -\beta \sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \right) \nonumber \\&\quad +S_{51} = 0, \end{aligned}$$

(32)

$$\begin{aligned} {\text {Sh}}_{\text {Hacc1}}(x=0) = 0 \, \, \therefore\, \, S_{11}+S_{61} = 0, \end{aligned}$$

(33)

$$\begin{aligned} {\text {Sh}}_{\text {Hacc1}}'(x=0) = 0 \, \, \therefore\, \, S_{21}\beta +S_{41}\alpha + S_{51} = 0. \end{aligned}$$

(34)

The conditions presented above can also be expressed in a matrix form, which can be applied for the other interpolation functions in this case:

$$\begin{aligned} \left[ {\text {Sh}}_{{\text {Hacc1}}}\right] \! \begin{bmatrix} S_{11}\!&S_{21}\!&S_{31}\!&S_{41}\!&S_{51}\!&S_{61} \end{bmatrix}\!^{\text {T}}\!\! = \begin{bmatrix} 1&0&0&0&0&0 \end{bmatrix}\!^{\text {T}} ,\end{aligned}$$

(35)

with:

$$\begin{aligned} \left[ {\text {Sh}}_{\text {Hacc1}}\right] = \left[ \begin{matrix} s_{11} &{} s_{12} &{}s_{13} &{}s_{14} &{} -\frac{L}{2} &{} 1 \\ s_{21} &{} s_{22} &{}s_{23} &{}s_{24} &{} 1 &{} 0 \\ s_{31} &{} s_{32} &{}s_{33} &{}s_{34} &{} \frac{L}{2} &{} 1\\ s_{41} &{} s_{42} &{}s_{43} &{}s_{44} &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} \beta &{} 0 &{} \alpha &{} 1 &{} 0 \end{matrix} \right] ,\end{aligned}$$

(36)

where:

$$\begin{aligned} s_{11}=s_{31}=ch_\frac{L}{2}c_\frac{L}{2} \end{aligned}$$

(37)

$$\begin{aligned} s_{32}=-s_{12}=ch_\frac{L}{2}s_\frac{L}{2}, \end{aligned}$$

(38)

$$\begin{aligned} s_{13}=s_{31}=sh_\frac{L}{2}s_\frac{L}{2} \end{aligned}$$

(39)

$$\begin{aligned} s_{34}=-s_{14}=sh_\frac{L}{2}c_\frac{L}{2}, \end{aligned}$$

(40)

$$\begin{aligned} s_{41}=-s_{21}=\alpha s_{34}-\beta s_{32}, \end{aligned}$$

(41)

$$\begin{aligned} s_{42}=s_{22}=\alpha s_{13}+\beta s_{11}, \end{aligned}$$

(42)

$$\begin{aligned} s_{43}=-s_{23}=\alpha s_{32}-\beta s_{34}, \end{aligned}$$

(43)

$$\begin{aligned} s_{44}=s_{24}=\alpha s_{11}-\beta s_{31} \end{aligned}$$

(44)

and: $ch_\frac{L}{2}=\cosh (\frac{\alpha L}{2})$, $sh_\frac{L}{2}=\sinh (\frac{\alpha L}{2})$, $c_\frac{L}{2} = \cos (\frac{\beta L}{2})$, and $s_\frac{L}{2} = \sin (\frac{\beta L}{2})$. The matrix in Eq. (36) is symbolically inverted, which leads to the values of the six constants for the first shape function. It is interesting to observe that the only difference among the six shape functions is the vector in the right side of Eq. (35). This vector will be: $\begin{bmatrix} 0&1&0&0&0&0\end{bmatrix}^{\text {T}}$, $\begin{bmatrix} 0&0&1&0&0&0 \end{bmatrix}^{\text {T}}$, $\begin{bmatrix} 0&0&0&1&0&0 \end{bmatrix}^{\text {T}}$, $\begin{bmatrix} 0&0&0&0&1&0 \end{bmatrix}^{\text {T}}$ and $\begin{bmatrix} 0&0&0&0&0&1 \end{bmatrix}^{\text {T}}$ for shape functions 2, 3, 4, 5, and 6, respectively. By solving the above system for the other five interpolation functions, it is possible to represent all constant values of the shape functions in a coefficient matrix, ${\text {Sh}}_{{\text {NHacc}}}$, which is referred to here as the completeness coefficient matrix:

$$\begin{aligned} \left[ {\text {Sh}}_{{\text {NHacc}}} \right] = \frac{ \left[ \begin{matrix} S_{11} &{} S_{12} &{} S_{11} &{} -S_{12} &{} -2S_{11} &{} 0 \\ S_{21} &{} S_{22} &{} -S_{21} &{} S_{22} &{} 0 &{} S_{26} \\ S_{31} &{} S_{32} &{} S_{31} &{} -S_{32} &{} -2S_{31} &{} 0 \\ S_{41} &{} S_{42} &{} -S_{41} &{} S_{42} &{} 0 &{} S_{46} \\ S_{51} &{} S_{52} &{} S_{51} &{} S_{52} &{} 0 &{} S_{56} \\ -S_{11} &{} -S_{12} &{} -S_{11} &{} S_{12} &{} S_{65} &{} 0 \end{matrix}\right] }{{\text {K}}_{{\text {NHacc}}}} ,\end{aligned}$$

(45)

with:

$$\begin{aligned} K_{\text {NHacc}}&= 2 \left( \alpha \sin \left( \frac{\beta L}{2}\right) -\beta \sinh \left( \frac{\alpha L}{2}\right) \right) \nonumber \\&\quad \times \left( \cos \left( \frac{\beta L}{2}\right) -\cosh \left( \frac{\alpha L}{2}\right) \right) , \end{aligned}$$

(46)

$$\begin{aligned} S_{11}\! = \! \beta \! \sinh \left( \!\frac{\alpha L}{2}\!\right) \! \cos \left( \!\frac{\beta L}{2}\!\right) \!+\alpha \! \cosh \left( \frac{\alpha L}{2}\right) \! \sin \left( \!\frac{\beta L}{2}\right) , \end{aligned}$$

(47)

$$\begin{aligned} S_{12} =\sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(48)

$$\begin{aligned} S_{65} = \alpha \sin (\beta L)+\beta \sinh (\alpha L), \end{aligned}$$

(49)

$$\begin{aligned} S_{21}&= \frac{K_{\text {NHacc}}}{D_{S1}}\sinh \left( \frac{\alpha L}{2}\right) \nonumber \\&\quad \times \left( \beta S_{12}^2 + \alpha S_{12} -\frac{\alpha }{4} \sinh (\alpha L) \sin (\beta L)\right) , \end{aligned}$$

(50)

where:

$$\begin{aligned} D_{S1}&=-\alpha \sinh ^4\left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \sin (\beta L)\nonumber \\&\quad +\sinh ^3\left( \frac{\alpha L}{2}\right) \left( L \left( \alpha ^2+\beta ^2\right) \sin ^2\left( \frac{\beta L}{2}\right) +\beta \sin (\beta L)\right) \nonumber \\&\quad -\alpha \sinh (\alpha L) \sinh \left( \frac{\alpha L}{2}\right) \sin ^2\left( \frac{\beta L}{2}\right) \nonumber \\&\quad +-\beta \sinh (\alpha L) \sinh ^2\left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \nonumber \\&\quad +\frac{\alpha }{4} \sinh ^2(\alpha L) \sin \left( \frac{\beta L}{2}\right) \sin (\beta L), \end{aligned}$$

(51)

$$\begin{aligned} S_{22} =S_{21} \frac{\frac{\alpha L}{2}- \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) }{\beta S_{12}+\alpha S_{32}}, \end{aligned}$$

(52)

$$\begin{aligned} S_{26} = S_{21}L-2S_{22} \end{aligned}$$

(53)

$$\begin{aligned} S_{46} = S_{41}L-2S_{42}, \end{aligned}$$

(54)

$$\begin{aligned} S_{31} \! = \! \beta \! \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) - \alpha \! \sinh \left( \!\frac{\alpha L}{2}\!\right) \! \cos \left( \!\frac{\beta L}{2}\!\right) , \end{aligned}$$

(55)

$$\begin{aligned} S_{32} = 1-\cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(56)

$$\begin{aligned} S_{41}&=\frac{K_{\text {NHacc}}}{D_{S1}}\sinh \left( \frac{\alpha L}{2}\right) \nonumber \\&\quad \times \left( \alpha S_{12}^2 -\beta S_{12}+\frac{\beta }{4} \sinh (\alpha L) \sin (\beta L)\right) , \end{aligned}$$

(57)

$$\begin{aligned} S_{42} =S_{41}\frac{\frac{\beta L}{2}-\cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) }{-\alpha S_{12}+\beta S_{32}}, \end{aligned}$$

(58)

$$\begin{aligned} S_{51} = -\frac{K_{\text {NHacc}}}{D_{S1}}\sinh \left( \frac{\alpha L}{2}\right) \left( \alpha ^2+\beta ^2\right) S_{12}^2, \end{aligned}$$

(59)

$$\begin{aligned} S_{52} = S_{51} \frac{\alpha \coth \left( \frac{\alpha L}{2}\right) -\beta \cot \left( \frac{\beta L}{2}\right) }{\alpha ^2+\beta ^2}, \end{aligned}$$

(60)

$$\begin{aligned} S_{56} = S_{51}L-2S_{52}+K_{\text {NHacc}}. \end{aligned}$$

(61)

Consequently, the amplification function V(x) can now be expressed by the nodal generalized displacements:

$$\begin{aligned} V(x) = \left[ Tx_{\text {NHa}} \right] \left[ {\text {Sh}}_{\text {NHacc}} \right] \left[ \vartheta \right] . \end{aligned}$$

(62)

$\left[ Tx_{\text {NHa}} \right]$ is the term vector in case A, which is dependent on the length x, and $\left[ \delta \vartheta \right]$ is the variation vector that is given by the initial and final displacements. These two vectors are presented below:

$$\begin{aligned} \left[ Tx_{\text {Ha}} \right] \! = \! \begin{bmatrix} \cosh (\alpha x)\cos (\beta x) \\ \cosh (\alpha x)\sin (\beta x) \\ \sinh (\alpha x)\sin (\beta x) \\ \sinh (\alpha x)\cos (\beta x) \\ x \\ 1 \end{bmatrix}^{\text {T}} \end{aligned}$$

(63)

$$\begin{aligned} \left[ \vartheta \right] = \begin{bmatrix} V_{\!-L/2} \\ V'_{\!-L/2} \\ V_{L/2} \\ V'_{L/2} \\ V_{0} \\ V'_{0} \\ \end{bmatrix} \end{aligned}$$

(64)

The amplification function, V(x), is conveniently represented in Eq. (62). It splits into three terms. The first is a vector in Eq. (63), which is only a function of x. The second is the completeness coefficient matrix for the boundary conditions, Eq. (45), which is independent of x. The third is a vector in Eq. (64), which contains the variational terms. For different cases of dominant torsion and/or distortion, as well as different boundary conditions, it is only necessary to change the respective vector or/and matrix in the formulation above.

A variation of V(x) is easily given by:

$$\begin{aligned} \delta V(x) = \left[ Tx_{\text {Ha}} \right] \left[ {\text {Sh}}_{{\text {Hacc}}} \right] . \end{aligned}$$

(65)

Introducing Eqs. (62) and (65) into the variational formulation presented in Eq. (26) leads to:

• For the first term in the integral:

$$\begin{aligned}&\int \limits _L E{}^iC{}^iV''(x) \delta {}^iV''(x) {\text {d}}x \nonumber \\&\quad =\!E{}^iC\!\!\int \limits _{-\frac{L}{2}}^{\frac{L}{2}} \!\!\left[ {}^i\left[ Tx_{N\!H\!1}'' \right] {}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] {}^i\left[ \vartheta \right] \right] ^{\text {T}}{}^i\left[ Tx_{N\!H\!1}'' \right] {}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] \! {\text {d}}x\!\! \nonumber \\&\quad = E\,{}^iC \,{}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{\text {NHa}}'' \right] \,{}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] \,{}^i\left[ \vartheta \right] . \end{aligned}$$

(66)

The values of the integration matrix $\left[ \Upsilon _{\text {NHa}}'' \right] =\int \nolimits _{-\frac{L}{2}}^{\frac{L}{2}} \left[ Tx_{\text {NHa}}'' \right] ^{\text {T}} \left[ Tx_{\text {NHa}}'' \right] {\text {d}}x$ are given below:

$$\begin{aligned} \left[ \Upsilon _{\text {NHa}}'' \right] = \begin{bmatrix} \Upsilon _{{\text {Ha}},11}''&0&\Upsilon _{{\text {Ha}},13}''&0&0&0\\&\Upsilon _{{\text {Ha}},22}''&0&\Upsilon _{{\text {zHa}},24}''&0&0\\&&\Upsilon _{{\text {Ha}},33}''&0&0&0\\&&&\Upsilon _{{\text {Ha}},44}''&0&0\\&&&&0&0 \\ {\text {Sym.}}&&&&&0 \end{bmatrix} ,\end{aligned}$$

(67)

where

$$\begin{aligned} \Upsilon _{{\text {Ha}},\!1\!1}''&= \frac{1}{4 \alpha \beta } \!\left( \beta \! \sinh (\alpha L) \left( \!\alpha ^2 \left( \!\alpha ^2\!-\!3 \beta ^2\right) \cos (\beta L)+\left( \!\alpha ^2\!+\!\beta ^2\!\right) ^2\right) \!\right. \nonumber \\&\quad + \left. \alpha \sin (\beta L) \left( \left( \alpha ^2+\beta ^2\right) ^2+\left( \beta ^4-3 \alpha ^2 \beta ^2\right) \cosh (\alpha L)\right) +\alpha \beta L\right. \nonumber \\&\quad + \left. \left( \alpha ^4-6 \alpha ^2 \beta ^2+\beta ^4\right) \right) , \end{aligned}$$

(68)

$$\begin{aligned} \Upsilon _{{\text {Ha}},13}''&= \frac{1}{4} \left( -\beta \left( \beta ^2-3 \alpha ^2\right) \sinh (\alpha L) \cos (\beta L) \right. \nonumber \\&\quad +\left. \alpha \left( \alpha ^2\!-\!3 \beta ^2\right) \cosh (\alpha L)\! \sin (\beta L)+ 4\alpha \beta L (\alpha \! -\!\beta ) (\alpha \! +\!\beta )\right) , \end{aligned}$$

(69)

$$\begin{aligned} \Upsilon _{H\!a,22}'' = -\!\Upsilon _{H\!a,1\!1}''\! +\!\frac{\left( \alpha ^2\!+\!\beta ^2\right) ^2 \!\!\sinh (\alpha L)\!+\!\alpha L \left( \alpha ^4\!-\!6 \alpha ^2\! \beta ^2\!+\!\beta ^4\right) }{2 \alpha }, \end{aligned}$$

(70)

$$\begin{aligned} \Upsilon _{{\text {Ha}},24}'' = \Upsilon _{{\text {Ha}},13}'' + 2 \alpha \beta L \left( \beta ^2-\alpha ^2\right) , \end{aligned}$$

(71)

$$\begin{aligned} \Upsilon _{{\text {Ha}},\!33}'' \! = \! -\!\Upsilon _{{\text {Ha}},\!11}''\! +\!\frac{\left( \alpha ^2\!+\!\beta ^2\right) ^2 (\alpha \sin (\beta L)\!+\!\beta \sinh (\alpha L))}{2 \alpha \beta }, \end{aligned}$$

(72)

$$\begin{aligned} \Upsilon _{{\text {Ha}}\!,44}'' = \Upsilon _{{\text {Ha}},11}''\!-\!\frac{\left( \alpha ^2\!+\!\beta ^2\right) ^2 \sin (\beta L)\!+\!\beta L \left( \alpha ^4\!-\!6 \alpha ^2 \beta ^2\!+\!\beta ^4\right) }{2 \beta }. \end{aligned}$$

(73)

The stiffness matrix due to longitudinal displacement is obtained from the multiplication

$$\begin{aligned} \,{}^i\left[ K_c \right] = E\,{}^iC \,{}^i\left[ {\text {Sh}}_{\text {Hacc}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{{\text {Ha}}}'' \right] \,{}^i\left[ {\text {Sh}}_{\text {Hacc}} \right] . \end{aligned}$$

(74)

• For the second term in the integral, one can proceed in a similar way:

$$\begin{aligned}&\int \limits _L G\,{}^iD\,{}^iV'(x) \delta {}^iV'(x) \, {\text {d}}x \nonumber \\&\quad =G\,{}^iD \,{}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{\text {NHa}}' \right] \,{}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] \,{}^i\left[ \vartheta \right] . \end{aligned}$$

(75)

The values of the integration matrix

$\left[ \Upsilon _{\text {NHa}}' \right] =\int \nolimits _{-\frac{L}{2}}^{\frac{L}{2}} \left[ Tx_{\text {NHa}}' \right] ^{\text {T}} \left[ Tx_{\text {NHa}}' \right] {\text {d}}x$ are given below:

$$\begin{aligned} \left[ \Upsilon _{{\text {NHa}}}' \right] \! = \! \begin{bmatrix} \Upsilon _{{\text {Ha}},1\!1}'&0&\Upsilon _{{\text {Ha}},13}'&0&0&0\\&\Upsilon _{{\text {Ha}},22}'&0&\Upsilon _{{\text {Ha}},24}'&\Upsilon _{{\text {NHa}},25}'&0 \\&&\Upsilon _{{\text {Ha}},33}'&0&0&0\\&&&\Upsilon _{{\text {Ha}},44}'&\Upsilon _{{\text {NHa}},45}'&0\\&&&&L&0 \\ {\text {Sym.}}&&&&&0 \end{bmatrix} ,\end{aligned}$$

(76)

where

$$\begin{aligned} \Upsilon _{{\text {Ha}},1\!1}'&= \frac{-1}{4 \alpha \beta } \left( \alpha \sin (\beta L) \left( \alpha ^2+\beta ^2 \cosh (\alpha L)+\beta ^2\right) \right. \nonumber \\&\quad -\left. \alpha \beta L \left( \beta ^2\!-\!\alpha ^2\right) \!+\!\beta \! \sinh (\alpha L) \left( \alpha ^2\! \cos (\beta L)\!+\!\alpha ^2\!+\!\beta ^2\right) \right), \end{aligned}$$

(77)

$$\begin{aligned} \Upsilon _{{\text {Ha}},1\!3}' = \frac{ \!\alpha \cosh (\alpha L) \sin (\beta L)-\!2 \alpha \beta L\!+\!\beta \sinh (\alpha L) \cos (\beta L)\!}{4}, \end{aligned}$$

(78)

$$\begin{aligned} \Upsilon _{{\text {Ha}},22}' = -\Upsilon _{{\text {Ha}},11}'\!+\!\frac{\alpha L \left( \beta ^2\!-\!\alpha ^2\right) \!+\!\left( \alpha ^2\!+\!\beta ^2\right) \sinh (\alpha L)}{2 \alpha }, \end{aligned}$$

(79)

$$\begin{aligned} \Upsilon _{{\text {Ha}},24}' = \Upsilon _{{\text {Ha}},13}' + \alpha \beta L, \end{aligned}$$

(80)

$$\begin{aligned} \Upsilon _{H\!a,33}' \! = \! -\Upsilon _{{\text {Ha}},11}'\! -\frac{\left( \alpha ^2\!+\!\beta ^2\right) (\alpha \sin (\beta L)\!-\!\beta \sinh (\alpha L))}{2 \alpha \beta }, \end{aligned}$$

(81)

$$\begin{aligned} \Upsilon _{{\text {Ha}},44}' = \Upsilon _{{\text {Ha}},11}' + \frac{\beta L \left( \alpha ^2-\beta ^2\right) +\left( \alpha ^2+\beta ^2\right) \sin (\beta L)}{2 \beta }, \end{aligned}$$

(82)

$$\begin{aligned} \Upsilon _{{\text {NHa}},25}'=2 \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(83)

$$\begin{aligned} \Upsilon _{{\text {NHa}},45}'=2 \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) . \end{aligned}$$

(84)

The stiffness matrix due to longitudinal rotation is obtained from the multiplication

$$\begin{aligned} \,{}^i\left[ K_d \right] = G\,{}^iD \,{}^i\left[ {\text {Sh}}_{\text {NHcc }}\right] ^{\text {T}} \,{}^i\left[ \Upsilon _{\text {NHa}}' \right] \,{}^i\left[ {\text {Sh}}_{\text {NHcc}}\right] . \end{aligned}$$

(85)

• The third term in the integral follows the same procedure:

$$\begin{aligned}&\int \limits _L \,{}^iB\,{}^iV(x) \delta {}^iV(x) \, {\text {d}}x \nonumber \\&\quad \,{}^iB \,{}^i\left[ {\text {Sh}}_{{\text {Hacc}}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{{\text {Ha}}} \right] \,{}^i\left[ {\text {Sh}}_{\text {Hacc}} \right] \,{}^i\left[ \vartheta \right] . \end{aligned}$$

(86)

The values of the integration matrix

$\left[ \Upsilon _{\text {NHa}} \right] =\int \nolimits _{-\frac{L}{2}}^{\frac{L}{2}} \left[ Tx_{\text {NHa}} \right] ^{\text {T}} \left[ Tx_{\text {NHa}} \right] {\text {d}}x$ are given below:

$$\begin{aligned} \left[ \Upsilon _{\text {NHa}} \right] = \begin{bmatrix} \Upsilon _{{\text {Ha}},11}&0&\Upsilon _{{\text {Ha}},13}&0&0&\Upsilon _{{\text {NHa}},16}\\&\Upsilon _{{\text {Ha}},22}&0&\Upsilon _{{\text {Ha}},13}&\Upsilon _{{\text {NHa}},25}&0 \\&&\Upsilon _{{\text {Ha}},33}&0&0&\Upsilon _{{\text {NHa}},36}\\&&&\Upsilon _{{\text {Ha}},44}&\Upsilon _{{\text {NHa}},45}&0\\&&&&\frac{L^3}{12}&0\\ {\text {Sym.}}&&&&&L \end{bmatrix} ,\end{aligned}$$

(87)

where

$$\begin{aligned} \Upsilon _{{\text {Ha}},11}&= \frac{1}{4 \alpha \beta \left( \alpha ^2+\beta ^2\right) } \left( \alpha \left( \alpha ^2+\beta ^2\right) (\beta L+\sin (\beta L))\right. \nonumber \\&\quad +\left. \beta \sinh (\alpha L) \left( \alpha ^2\! \cos (\beta L)\!+\!\alpha ^2\!+\!\beta ^2\right) \!+\!\alpha \beta ^2\! \cosh (\alpha L)\! \sin (\beta L)\right) , \end{aligned}$$

(88)

$$\begin{aligned} \Upsilon _{{\text {Ha}},13} =\frac{\alpha \cosh (\alpha L) \sin (\beta L)-\beta \sinh (\alpha L) \cos (\beta L)}{4 \left( \alpha ^2+\beta ^2\right) }, \end{aligned}$$

(89)

$$\begin{aligned} \Upsilon _{{\text {Ha}},22} = -\Upsilon _{{\text {Ha}},11} +\frac{\alpha L+\sinh (\alpha L)}{2 \alpha }, \end{aligned}$$

(90)

$$\begin{aligned} \Upsilon _{{\text {Ha}},33} = -\Upsilon _{{\text {Ha}},11} + \frac{\alpha \sin (\beta L)+\beta \sinh (\alpha L)}{2 \alpha \beta }, \end{aligned}$$

(91)

$$\begin{aligned} \Upsilon _{{\text {Ha}},44} = \Upsilon _{{\text {Ha}},11} -\frac{\sin (\beta L)-\beta L}{2 \beta }, \end{aligned}$$

(92)

$$\begin{aligned} \Upsilon _{{\text {NHa}},16} =\frac{\alpha \Upsilon _{{\text {NHa}},45}'+\beta \Upsilon _{{\text {NHa}},25}'}{\alpha ^2+\beta ^2}, \end{aligned}$$

(93)

$$\begin{aligned} \Upsilon _{{\text {NHa}},25} =\frac{\Upsilon _{{\text {NHa}},25}'}{\left( \alpha ^2+\beta ^2\right) ^2}\left( \beta ^2-\alpha ^2-\frac{ \beta L}{2} \left( \alpha ^2+\beta ^2\right) \cot \left( \frac{\beta L}{2}\right) \right. \nonumber \\ \left. +\alpha \tanh \left( \frac{\alpha L}{2}\right) \left( \frac{L}{2} \left( \alpha ^2+\beta ^2\right) +2 \beta \cot \left( \frac{\beta L}{2}\right) \right) \right) , \end{aligned}$$

(94)

$$\begin{aligned} \Upsilon _{{\text {NHa}},36} =\frac{\alpha \Upsilon _{{\text {NHa}},25}'-\beta \Upsilon _{{\text {NHa}},45}'}{\alpha ^2+\beta ^2}, \end{aligned}$$

(95)

$$\begin{aligned} \Upsilon _{{\text {NHa}},45} = \frac{\Upsilon _{{\text {NHa}},45}'}{\left( \alpha ^2+\beta ^2\right) ^2}\left( \frac{\beta L}{2} \left( \alpha ^2+\beta ^2\right) \tan \left( \frac{\beta L}{2}\right) - \alpha ^2+\beta ^2\right. \nonumber \\ \left. +\alpha \coth \left( \frac{\alpha L}{2}\right) \left( \frac{L}{2} \left( \alpha ^2+\beta ^2\right) -2 \beta \tan \left( \frac{\beta L}{2}\right) \right) \right) . \end{aligned}$$

(96)

The stiffness matrix due to transverse distortion is obtained from the multiplication:

$$\begin{aligned} \,{}^i\left[ K_b \right] = \,{}^iB \,{}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{\text {NHa}} \right] \,{}^i\left[ {\text {Sh}}_{\text {NHacc}} \right] . \end{aligned}$$

(97)

The fourth term in the integral in Eq. (18) has a unique property. It involves a shape function and its second derivative, as well as its commutative product. Each stiffness matrix is not symmetric, but each is the transpose of the other. This leads to the final symmetric matrix in the summation:

$$\begin{aligned}&\mu K\,{}^iD_\mu \int \limits _L \,{}^iV(x) \delta {}^iV(x) \, {\text {d}}x \nonumber \\&\quad =\mu K\,{}^iD_\mu \,{}^i\left[ {\text {Sh}}_{{\text {Hacc}}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{\text {NHa}}'','\right] \,{}^i\left[ {\text {Sh}}_{{\text {Hacc}}} \right] \,{}^i\left[ \vartheta \right] . \end{aligned}$$

(98)

The values of the integration matrix

$\left[ \Upsilon _{N\!Ha}'','\right] = \int \nolimits _{-\frac{L}{2}}^{\frac{L}{2}} \left[ T\!x_{N\!Ha}'' \right] ^{\text {T}} \left[ T\!x_{N\!Ha} \right] \! +\! \left[ T\!x_{N\!Ha} \right] ^{\text {T}} \left[ T\!x_{N\!Ha}''\right] {\text {d}}x$ are given below:

$$\begin{aligned} \left[ \Upsilon _{\text {NHa}}'','\right] = \begin{bmatrix} \Upsilon _{H\!a,1\!1}'','&\! 0\!&\Upsilon _{H\!a,13}'','&0&0&\!\! \Upsilon _{N\!Ha,16}'','\\ & \Upsilon _{H\!a,22}'','&0&\Upsilon _{H\!a,24}'','&\Upsilon _{N\!H\!a,25}'','&\!\!0 \\&&\Upsilon _{H\!a,33}'','&0&0&\!\!\Upsilon _{N\!H\!a,36}'','\\&&&\Upsilon _{H\!a,44}'','&\Upsilon _{N\!H\!a,45}'','&\!\!0\\&&&&0&\!\! 0\\ {\text {Sym.}}&&&&&\!\! 0 \end{bmatrix} ,\end{aligned}$$

(99)

where

$$\begin{aligned} \Upsilon _{{\text {Ha}},11}'','&= \frac{1}{2 \alpha \beta } \left[ \beta \sinh (\alpha L) \left( \alpha ^2 \cos (\beta L)+\alpha ^2-\beta ^2\right) \right. \nonumber \\&\quad -\left. \alpha \beta ^2 \cosh (\alpha L) \sin (\beta L)\!+\!\alpha (\alpha ^2\! -\!\beta ^2 ) (\beta L\!+\!\sin (\beta L))\right] , \end{aligned}$$

(100)

$$\begin{aligned} \Upsilon _{H\!a,13}'','\! = \!\frac{2 \alpha \beta L\!+\!\beta \! \sinh (\alpha L) \!\cos (\beta L)\!+\!\alpha \! \cosh (\alpha L)\! \sin (\beta L)}{2}, \end{aligned}$$

(101)

$$\begin{aligned} \Upsilon _{{\text {Ha}},22}'',' = \frac{\left( \alpha ^2-\beta ^2\right) (\alpha L+\sinh (\alpha L))}{\alpha } - \Upsilon _{{\text {Ha}},11}'',' \end{aligned}$$

(102)

$$\begin{aligned} \Upsilon _{{\text {Ha}},44}'',' = \Upsilon _{{\text {Ha}},11}'','-\frac{\left( \alpha ^2-\beta ^2\right) (\beta L+\sin (\beta L))}{\beta }, \end{aligned}$$

(103)

$$\begin{aligned} \Upsilon _{{\text {Ha}},24}'',' = \Upsilon _{{\text {Ha}},13}'',' -2 \alpha \beta L, \end{aligned}$$

(104)

$$\begin{aligned} \Upsilon _{{\text {Ha}},33}'',' = \Upsilon _{{\text {Ha}},22}'','+\frac{\left( \alpha ^2-\beta ^2\right) (\beta L-\sin (\beta L))}{\beta }, \end{aligned}$$

(105)

$$\begin{aligned} \Upsilon _{{\text {NHa}},16}'',' = \alpha \Upsilon _{{\text {NHa}},45}'-\beta \Upsilon _{{\text {NHa}},25}', \end{aligned}$$

(106)

$$\begin{aligned} \Upsilon _{{\text {NHa}},36}'',' =\beta \Upsilon _{{\text {NHa}},45}'+\alpha \Upsilon _{{\text {NHa}},25}', \end{aligned}$$

(107)

$$\begin{aligned} \Upsilon _{{\text {NHa}},25}'','&=\alpha L \sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \nonumber \\&\quad +\beta L\cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) -\Upsilon _{{\text {NHa}},25}', \end{aligned}$$

(108)

$$\begin{aligned} \Upsilon _{{\text {NHa}},45}'','&=\alpha L \cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \nonumber \\&\quad -\beta L\sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) -\Upsilon _{{\text {NHa}},45}'. \end{aligned}$$

(109)

The stiffness matrix due to the Poisson effect in plate behavior is obtained from multiplication, similar to the other matrices:

$$\begin{aligned} \,{}^i\left[ K_\mu \right] \! = \! \mu K{}^iD_\mu {}^i\left[ {\text {Sh}}_{{\text {NHacc}}} \right] ^{\text {T}} \,{}^i\left[ \Upsilon _{{\text {NHa}}}'','\right] \,{}^i\left[ {\text {Sh}}_{{\text {NHacc}}} \right] . \end{aligned}$$

(110)

The total stiffness matrix can be expressed by a combination of Eqs. (74), (85), (97), and (110):

$$\begin{aligned} \,{}^i[K_{\text {NHacc}}]&= \,{}^i[{\text {Sh}}_{\text {NHacc}}]^{\text {T}} \left[ E\,{}^iC \,{}^i[\Upsilon _{\text {NHa}}''] + G\,{}^iD \,{}^i[\Upsilon _{\text {NHa}}'] \right. \nonumber \\&\quad \left. + \,{}^iB \,{}^i\left[ \Upsilon _{\text {NHa}} \right] +\mu K\,{}^iD_\mu \,{}^i\left[ \Upsilon _{\text {NHa}}'','\right] \right] \,{}^i[{\text {Sh}}_{\text {NHacc}}]. \end{aligned}$$

(111)

Here, it is important to highlight that the integration matrices $\Upsilon _{\text {NHa}}$, $\Upsilon '_{\text {NHa}}$, $\Upsilon ''_{\text {NHa}}$ and $\Upsilon ''_{\text {NHa}},'$ [given, respectively, in Eqs. (87), (76), (67), and (99)] are not dependent on the boundary conditions. Therefore, the completeness coefficient matrix, which expresses the boundary conditions, can be understood as a matrix transformation of a kernel stiffness matrix:

$$\begin{aligned} \,{}^i[K_{\text {NHa}}]&=E\,{}^iC \,{}^i[\Upsilon _{\text {NHa}}''] + G\,{}^iD \,{}^i[\Upsilon _{\text {NHa}}'] + \,{}^iB \,{}^i\left[ \Upsilon _{\text {NHa}} \right] \nonumber \\&\quad +\mu K\,{}^iD_\mu \,{}^i\left[ \Upsilon _{\text {NHa}}'','\right] . \end{aligned}$$

(112)

The total stiffness matrix of the clamped–clamped of case A can be expressed by:

$$\begin{aligned} \,{}^i[K_{\text {NHacc}}] = \,{}^i[{\text {Sh}}_{\text {NHacc}}]^{\text {T}} \,\,{}^i[K_{\text {NHa}}] \,\,{}^i[{\text {Sh}}_{\text {NHacc}}]. \end{aligned}$$

(113)

force vector for case A:

As mentioned before, the main reason to use three nodes with two degrees of freedom each is to fulfill the inner product of the constant/linearly distributed force and the variation of the generalized displacement, which can be expressed by the shape function as:

$$\begin{aligned} \int \limits _L \,{}^iq(x) \delta {}^iV(x) {\text {d}}x \! = \!\! \int \limits _{-\frac{L}{2}}^{\frac{L}{2}} \!{}^i q(x) \,{}^i\left[ Tx_{{\text {NHa}}} \right] \,{}^i\left[ {\text {Sh}}_{{\text {Hacc}}} \right] {\text {d}}x. \end{aligned}$$

(114)

Just like in the development of the stiffness matrix, the completeness coefficient matrix of the boundary conditions is independent of the length. Therefore, one can find:

$$\begin{aligned} \,{}^i\left[ F_{\text {NHacc}} \right] = \,{}^i[{\text {Sh}}_{\text {NHacc}}]^{\text {T}} \,{}^i\left[ Fk_{\text {NHa}} \right] , \end{aligned}$$

(115)

where the components of the vector are

$\,{}^i\left[ Fk_{\text {NHa}} \right] ^{\text {T}} = [Fk_1, Fk_2, Fk_3, Fk_4, Fk_5, Fk_6]$ for a linear load function: $\,{}^iq=ax+b$ are

$$\begin{aligned} Fk_1 \! = \!2b\frac{ \alpha \! \sinh \left( \frac{\alpha L}{2}\right) \! \cos \left( \frac{\beta L}{2}\right) \!+\!\beta \! \cosh \left( \frac{\alpha L}{2}\right) \! \sin \left( \frac{\beta L}{2}\right) }{\alpha ^2+\beta ^2}, \end{aligned}$$

(116)

$$\begin{aligned} Fk_2&= \frac{a}{\left( \alpha ^2+\beta ^2\right) ^2} \left( \alpha \sinh \left( \frac{\alpha L}{2}\right) \left( L \left( \alpha ^2+\beta ^2\right) \sin \left( \frac{\beta L}{2}\right) \right. \right. \nonumber \\&\quad +\left. \left. 4 \beta \cos \left( \frac{\beta L}{2}\right) \right) -\cosh \left( \frac{\alpha L}{2}\right) \left( \beta L \left( \alpha ^2+\beta ^2\right) \cos \left( \frac{\beta L}{2}\right) \right. \right. \nonumber \\&\quad +\left. \left. 2 (\alpha -\beta ) (\alpha +\beta ) \sin \left( \frac{\beta L}{2}\right) \right) \right) , \end{aligned}$$

(117)

$$\begin{aligned} Fk_3 = \frac{2 b \left( \alpha \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) -\beta \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right) }{\alpha ^2+\beta ^2}, \end{aligned}$$

(118)

$$\begin{aligned} Fk_4&= \frac{a}{\left( \alpha ^2+\beta ^2\right) ^2} \left( \sinh \left( \frac{\alpha L}{2}\right) \left( \beta L \left( \alpha ^2+\beta ^2\right) \sin \left( \frac{\beta L}{2}\right) \right. \right. \nonumber \\&\quad \left. \left. +2 \left( \beta ^2-\alpha ^2\right) \cos \left( \frac{\beta L}{2}\right) \right) \right. \nonumber \\&\quad +\left. \alpha \! \cosh \left( \!\frac{\alpha L}{2}\!\right) \left( \!L\! \left( \!\alpha ^2\!+\!\beta ^2\!\right) \! \cos \left( \!\frac{\beta L}{2}\!\right) \!-\!4 \beta \! \sin \left( \!\frac{\beta L}{2}\right) \!\right) \!\right) , \end{aligned}$$

(119)

$$\begin{aligned} Fk_5 = \frac{a L^3}{12} \end{aligned}$$

(120)

$$\begin{aligned} Fk_6 = L. \end{aligned}$$

(121)

As a particular case, the constant function $\,{}^iq=a$ causes 2nd, 4th and 5th in the vector above to vanish.

Inhomogeneous solution for case A with hinged–hinged boundary conditions

When one adopts different boundary conditions at the element nodes, the advantages of presenting the stiffness matrix in the form of Eq. (112) stand out simply by changing the coefficient completeness matrix.

In the case of hinged–hinged² boundary conditions, the null propriety of the first derivate of longitudinal restraint at the initial and final nodes cannot be applied for any displacement fields, similar to the case of the clamped–clamped beam. Instead, the generalized internal moment must be eliminated, which implies that the second derivate of the shape function must be null at the hinged nodes.

For instance, the first two shape functions of case A, presented in Eq. (28), must satisfy the following conditions for the initial node:

${\text {Sh}}_{{\text {Hahh1}}}$:

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc1}}}\left( x\! = \!-\frac{L}{2}\right) \! =\! 1 \end{aligned}$$

(122)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc1}}}''\left( x\! = \!-\frac{L}{2}\right) \! =\! 0, \end{aligned}$$

(123)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc1}}}\left( x\! = \!0\right) \! =\! 0 \end{aligned}$$

(124)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc1}}}'\left( x\! = \!0\right) \! =\! 0, \end{aligned}$$

(125)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc1}}}\left( x\! = \!\frac{L}{2}\right) \! =\! 0 \end{aligned}$$

(126)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc1}}}''\left( x\! = \!\frac{L}{2}\right) \! =\! 0, \end{aligned}$$

(127)

${\text {Sh}}_{{\text {Hahc2}}}$:

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc2}}}\left( x\! = \!-\frac{L}{2}\right) \! =\! 0 \end{aligned}$$

(128)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc2}}}''\left( x\! = \!-\frac{L}{2}\right) \! =\! 0, \end{aligned}$$

(129)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc2}}}(x\! = \!0) = 0 \end{aligned}$$

(130)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc2}}}'(x\! = \!0)\! =\! 0, \end{aligned}$$

(131)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc2}}}\left( x\! = \!\frac{L}{2}\right) \! =\! 0 \end{aligned}$$

(132)

$$\begin{aligned} {\text {Sh}}_{{\text {Hahc2}}}''\left( x\! = \!\frac{L}{2}\right) \! =\! 0. \end{aligned}$$

(133)

The conditions presented above can also be expressed in matrix form, which can be applied to the other shape functions. By following the same procedure presented in the previous subsection and solving the six systems, each one with six equations, the hinged–hinged coefficient completeness matrix of boundary conditions is

$$\begin{aligned} \left[ {\text {Sh}}_{\text {NHahh}} \right] = \frac{ \begin{bmatrix} S_{11}&0&S_{11}&0&-2S_{11}&0 \\ S_{21}&0&-S_{21}&0&0&S_{21}L \\ S_{31}&0&S_{31}&0&-2S_{31}&0 \\ S_{41}&0&-S_{41}&0&0&S_{41}L \\ S_{51}&0&S_{51}&0&0&S_{56} \\ -S_{11}&0&-S_{11}&0&S_{65}&0 \end{bmatrix} }{{{K}}_{\text {NHahh}}} \end{aligned}$$

(134)

with

$$\begin{aligned} S_{65} = -2 \alpha \beta (\cosh (\alpha L)+\cos (\beta L)), \end{aligned}$$

(135)

$$\begin{aligned} S_{11}&= \left( \beta ^2-\alpha ^2\right) \sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \nonumber \\&\quad -2 \alpha \beta \cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(136)

$$\begin{aligned} K_{\text {NHahh}} = S_{65}-2S_{11}, \end{aligned}$$

(137)

$$\begin{aligned} S_{21}&= \frac{K_{{\text {NHahh}}}}{D_{S2}} \left( \left( \beta ^2-\alpha ^2\right) \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right. \nonumber \\&\quad +\left. 2 \alpha \beta \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \right) , \end{aligned}$$

(138)

$$\begin{aligned} D_{S2}&= L \left( \alpha ^2+\beta ^2\right) \left( \beta \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right. \nonumber \\&\quad \left. +\alpha \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \right) +S_{{\text {aux}}}, \end{aligned}$$

(139)

$$\begin{aligned} S_{{\text {aux}}} = -2 \alpha \beta (\cosh (\alpha L)-\cos (\beta L)) ,\end{aligned}$$

(140)

$$\begin{aligned} S_{31}&= (\alpha ^2 -\beta ^2 ) \cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \nonumber \\&\quad -2 \alpha \beta \sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(141)

$$\begin{aligned} S_{41}&= \frac{K_{{\text {NHahh}}}}{D_{S2}} \left( 2 \alpha \beta \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right. \nonumber \\&\quad \left. +(\alpha ^2 -\beta ^2 ) \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \right) , \end{aligned}$$

(142)

$$\begin{aligned} S_{51} = K_{{\text {NHahh}}} \!\frac{S_{{\text {aux}}}\!-\!D_{S2}}{D_{S2}L}, \end{aligned}$$

(143)

$$\begin{aligned} S_{56} = \frac{L S_{{\text {aux}}} S_{51}}{S_{{\text {aux}}}-D_{S2}}. \end{aligned}$$

(144)

By replacing ${\text {Sh}}_{\text {NHacc}}$ with ${\text {Sh}}_{\text {NHahh}}$ in Eq. (113), one obtains the exact stiffness matrix for an element with hinged–hinged boundary conditions. The same must be applied to the vector force presented in Eq. (115).

Inhomogeneous solution for case A with clamped–hinged boundary conditions

The coefficient completeness matrix for the clamped–hinged boundary conditions can be determined in the same way as the previous case. However, due to the non-symmetric boundary conditions in FEM, it leads to substantially more complex and longer terms, which indicates the disadvantage of the exact GBT solution.

It is important to note that, in spite of the complexity of the terms below, the stiffness matrix for these boundary conditions is only feasible with the use of a coefficient completeness matrix. A direct derivation of the stiffness matrix will lead to extremely long terms in the absence of a coefficient completeness matrix.

Following the same procedure, as in the hinged–hinged boundary conditions, one obtains the coefficient completeness matrix for the clamped–hinged boundary conditions:

$$\begin{aligned} \left[ {\text {Sh}}_{\text {NHach}} \right] \! = \! \frac{ \begin{bmatrix} S_{11}&S_{12}&S_{13}&0&S_{15}&S_{16} \\ S_{21}&S_{22}&S_{23}&0&S_{25}&S_{26} \\ S_{31}&S_{32}&S_{33}&0&S_{35}&S_{36} \\ S_{41}&S_{42}&S_{43}&0&S_{45}&S_{46} \\ S_{51}&S_{52}&S_{53}&0&S_{55}&S_{56} \\ -S_{11}&-S_{21}&-S_{13}&0&K_{{\text {NHach}}} - S_{15}&-S_{16} \end{bmatrix} }{K_{{\text {NHach}}}}. \end{aligned}$$

(145)

To evaluate this case, the following auxiliary terms are used:

$$\begin{aligned} b_{1} = \left( \alpha ^2+\beta ^2\right) \end{aligned}$$

(146)

$$\begin{aligned} b_{2} = \left( \alpha ^2-\beta ^2\right) , \end{aligned}$$

(147)

$$\begin{aligned} b_{3} = \left( 3\alpha ^2+\beta ^2\right) \end{aligned}$$

(148)

$$\begin{aligned} b_{4} = \left( 3\alpha ^2-\beta ^2\right) , \end{aligned}$$

(149)

$$\begin{aligned} b_{5} = \left( \alpha ^2+3\beta ^2\right) \end{aligned}$$

(150)

$$\begin{aligned} b_{6} = \left( \alpha ^2-3\beta ^2\right) , \end{aligned}$$

(151)

$$\begin{aligned} a_{1} = 2 b_{1} \left( \alpha \sin \left( \frac{\beta L}{2}\right) -\beta \sinh \left( \frac{\alpha L}{2}\right) \right) , \end{aligned}$$

(152)

$$\begin{aligned} a_{3} = 2 b_{1} (\alpha \sin (\beta L)-\beta \sinh (\alpha L)), \end{aligned}$$

(153)

$$\begin{aligned} a_{2} = 4 \sinh \left( \!\frac{\alpha L}{2}\!\right) \sin \left( \!\frac{\beta L}{2}\!\right) \! \left( \!\cos \left( \!\frac{\beta L}{2}\!\right) \!-\!\cosh \left( \!\frac{\alpha L}{2}\right) \!\!\right) , \end{aligned}$$

(154)

$$\begin{aligned} a_{4}\! =\! \text {csch}\left( \frac{\alpha L}{2}\right) \csc \left( \frac{\beta L}{2}\right) \!-\!\coth \left( \frac{\alpha L}{2}\right) \cot \left( \frac{\beta L}{2}\!\right) , \end{aligned}$$

(155)

$$\begin{aligned} a_{5} =-L b_{1} b_{2} \cosh (\alpha L) \cos (\beta L), \end{aligned}$$

(156)

$$\begin{aligned} a_{6}\! = \!-\beta ^2 L b_{1}\! \cos (\!\beta L) \end{aligned}$$

(157)

$$\begin{aligned} a_{8}\! = \!-4 \alpha \beta ^2 \sinh \! (\alpha L), \end{aligned}$$

(158)

$$\begin{aligned} a_{7}\! = \!-\alpha ^2\! L b_{1}\! \cosh (\!\alpha L) \end{aligned}$$

(159)

$$\begin{aligned} a_{16}\! = \! 4 \alpha ^2 \beta \sin (\beta L), \end{aligned}$$

(160)

$$\begin{aligned} a_{9}=-4 \alpha \beta ^2 \sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{3 \beta L}{2}\right) , \end{aligned}$$

(161)

$$\begin{aligned} a_{10}= -4 \alpha ^2 \beta \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{3 \beta L}{2}\right) , \end{aligned}$$

(162)

$$\begin{aligned} a_{11}=-2 \alpha \beta L b_{1} \sinh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(163)

$$\begin{aligned} a_{12}= -4 \alpha ^2 \beta \cosh \left( \frac{3 \alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(164)

$$\begin{aligned} a_{13}= -4 \alpha \beta ^2 \sinh \left( \frac{3 \alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(165)

$$\begin{aligned} a_{14}=-L b_{1} b_{2} \cosh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) , \end{aligned}$$

(166)

$$\begin{aligned} a_{15}= -2 \alpha \beta L b_{1} \sinh (\alpha L) \sin (\beta L), \end{aligned}$$

(167)

$$\begin{aligned} a_{17}= -2 \alpha b_2 \sin \left( \frac{3\beta L}{2}\right) \sinh \left( \frac{\alpha L}{2}\right) , \end{aligned}$$

(168)

$$\begin{aligned} a_{18}= 4\alpha \beta ^2 \sin \left( \frac{\beta L}{2}\right) \cosh \left( \frac{\alpha L}{2}\right) , \end{aligned}$$

(169)

$$\begin{aligned} a_{19}= 4\alpha ^2 \beta \cos \left( \frac{\beta L}{2}\right) \sinh \left( \frac{\alpha L}{2}\right) , \end{aligned}$$

(170)

$$\begin{aligned} a_{20}= 4\alpha ^2\beta \sin \left( 2\beta L\right) , \end{aligned}$$

(171)

$$\begin{aligned} a_{21}= -\alpha ^2 b_1 L \cos \left( \frac{3 \beta L}{2}\right) \cosh \left( \frac{\alpha L}{2}\right) , \end{aligned}$$

(172)

$$\begin{aligned} a_{22}= \beta ^2 b_1 L \cos \left( \frac{\beta L}{2}\right) \cosh \left( \frac{3 \alpha L}{2}\right) , \end{aligned}$$

(173)

$$\begin{aligned} a_{23}&= -\sinh \left( \frac{\alpha L}{2}\right) \left( 4 \alpha \cosh \left( \frac{\alpha L}{2}\right) \left( b_1 \cos (\beta L)-\alpha ^2\right. \right. \nonumber \\&\quad \left. \left. +4 \beta ^2 \cosh (\alpha L)\right) \right. \left. -2 b_1 \left( 2 \beta \sinh \left( \frac{\alpha L}{2}\right) \sin (\beta L)\right. \right. \nonumber \\&\quad +\left. \left. \sin \left( \!\frac{\beta L}{2}\!\right) \! (\!3 \alpha \beta L (\cos (\beta L)\!+\!1\!)\!-\!2 \alpha \sin (\beta L)\!-\!2 \beta \! \sinh (\!\alpha L))\!\right) \!\!\right) . \end{aligned}$$

(174)

Therefore, the terms in Eq. (145) are

$$\begin{aligned} {K_{{\text {NHach}}}}&= a_{23} - 2\left( a_5\!+\!a_6\!-\!a_7\!-\!a_{15}\!-\!a_{16}\right) +3\left( \!\frac{a_8}{2}\!+\!a_{10}\!-\!a_{13}\!\right) \nonumber \\&\quad + a_{11}\left( \!1\!-\!3\cosh \left( \alpha L\!\right) \!\right) \!+\!a_9\!-\!a_{12}\!-\!a_{14}\!+\!a_{20}\!+\!a_{21}\!+\!a_{22}, \end{aligned}$$

(175)

$$\begin{aligned} S_{11} = a_{5}\!+a_{6}-a_{7}-a_{8}-a_{9}-a_{10}\!+a_{12}\!+a_{13}-a_{15}-a_{16}, \end{aligned}$$

(176)

$$\begin{aligned} S_{16} =\frac{a_{11}}{ \alpha ^2 \beta ^2}\left( \frac{4\left( \beta ^2 a_{7}-\alpha ^2 a_{6}\right) }{\left( L b_{1} \right) ^2}+\frac{a_{16}-a_{8}}{4}\right) , \end{aligned}$$

(177)

$$\begin{aligned} S_{13} = S_{11} + a_{1}a_{2} \end{aligned}$$

(178)

$$\begin{aligned} S_{15} = -2 S_{11} - a_{1}a_{2}, \end{aligned}$$

(179)

$$\begin{aligned} S_{12} = -\frac{L}{2} a_{1}a_{2}-S_{16}, \end{aligned}$$

(180)

$$\begin{aligned} S_{25} = a_{3} \left( \alpha L-2\sinh \left( \frac{\alpha L}{2}\right) \cos \left( \frac{\beta L}{2}\right) \right) , \end{aligned}$$

(181)

$$\begin{aligned} S_{22} = \frac{4\alpha \beta S_{25}}{L b_{1} a_{3}} \left( \frac{a_{11} b_{2}}{2 \alpha ^2 \beta ^2}+\frac{2 a_{14}}{b_{2}}-\frac{a_{6}}{\beta ^2}-\frac{a_{7}}{\alpha ^2}\right) , \end{aligned}$$

(182)

$$\begin{aligned} S_{23}&= \frac{2 a_{6}b_3-3b_2a_{11}+a_{15}b_4}{\beta L b_1} -\frac{L^2b_1 \left( a_{8}+a_{16}\right) +8a_{15}}{4\beta L}\nonumber \\&\quad -a_{17}- \frac{4 \beta a_{14} \left( -2 \alpha ^4 a_{6}+L\left( \alpha \beta b_{1}\right) ^2-\beta ^2 b_{2}a_{7}\right) }{\left( L \alpha \beta b_1 \right) ^2 b_2}\nonumber \\&\quad +\frac{2\beta a_{7}}{\left( L \alpha \beta b_1 \right) ^2}\left( 2\alpha ^2\beta ^2 L b_1 -b_4 a_{6} - 2a_{11}\beta ^2 \right) , \end{aligned}$$

(183)

$$\begin{aligned} S_{26}\! = \! \frac{L}{2} \left( S_{21}-S_{23}\right) \!-S_{22} \end{aligned}$$

(184)

$$\begin{aligned} S_{21} = -\left( S_{23}+S_{25}\right) , \end{aligned}$$

(185)

$$\begin{aligned} S_{31}&= -\frac{\alpha \left( a_6-a_9\right) }{\beta }+\frac{b_3 a_8-b_5 a_{16}+b_2 a_{15}}{2\alpha \beta }+2\frac{\alpha \beta a_5}{b_2}-\frac{\beta a_7}{\alpha }\nonumber \\&\quad +a_{18}\left( 3+\frac{\alpha ^2}{\beta ^2}+2\cos \left( \beta L\right) -2\cosh \left( \alpha L\right) \right) \nonumber \\&\quad +a_{19}\left( 2+\frac{\beta ^2}{\alpha ^2}+2\cosh \left( \alpha L\right) \right) , \end{aligned}$$

(186)

$$\begin{aligned} S_{33} = S_{31} + a_1a_2a_4 \end{aligned}$$

(187)

$$\begin{aligned} S_{32} = S_{12} a_4, \end{aligned}$$

(188)

$$\begin{aligned} S_{35} = -\left( S_{31}+S_{33}\right) \end{aligned}$$

(189)

$$\begin{aligned} S_{36} = S_{16} a_4, \end{aligned}$$

(190)

$$\begin{aligned} S_{43}&= \frac{2}{\alpha L} \left( \vphantom{\quad -\left. \frac{a_{11}}{L b_1}\left( \frac{a_6}{\beta ^2}+\frac{a_7}{\alpha ^2}-\frac{4 a_{14}}{b_2}\right) \right) -\frac{\beta }{\alpha }S_{23},}a_5+a_6-a_7+a_{14}-a_{21}-a_{22}\right. \nonumber \\&\quad -\left. \frac{a_{11}}{L b_1}\left( \frac{a_6}{\beta ^2}+\frac{a_7}{\alpha ^2}-\frac{4 a_{14}}{b_2}\right) \right) -\frac{\beta }{\alpha }S_{23}, \end{aligned}$$

(191)

$$\begin{aligned} S_{45} = -a3 \left( \beta L-2 \cosh \left( \frac{\alpha L}{2}\right) \sin \left( \frac{\beta L}{2}\right) \right) , \end{aligned}$$

(192)

$$\begin{aligned} S_{42} = \frac{S_{22}S_{45}}{S_{25}} \end{aligned}$$

(193)

$$\begin{aligned} S_{41} = -\left( S_{45}+S_{43}\right) , \end{aligned}$$

(194)

$$\begin{aligned} S_{46} = \frac{L}{2} \left( S_{41}-S_{43}\right) -S_{42}, \end{aligned}$$

(195)

$$\begin{aligned} S_{5i} = -\left( \beta S_{2i} + \alpha S_{4i} \right) \text { for: } 1 \le i \le 5, \end{aligned}$$

(196)

$$\begin{aligned} S_{56} = K_{{\text {NHach}}} -\left( \beta S_{26} + \alpha S_{46} \right) . \end{aligned}$$

(197)

By replacing ${\text {Sh}}_{\text {NHacc}}$ with ${\text {Sh}}_{{\text {NHach}}}$ in Eq. (113), one obtains the exact stiffness matrix for an element with clamped–hinged boundary conditions. The same must be done for the vector force presented in Eq. (115).

Numerical example

As a detailed numerical example of the application of the exact stiffness matrix, let us consider the thin-walled circular hollow steel cross section shown in Fig. 2. This cross section is applied in a vertical cantilever structure subjected to a linear projected surface load, i.e., the total load applied in the structure is not a product of the surface load and the area of the surface, but is the product of the surface load and the project area on the global coordinate direction z. The material parameters are Young’s modulus $E = 205{,}000$ N/mm$^2$, Poisson’s ratio $\mu = 0.3$, and shear modulus $G = 78,846.2$ N/mm$^2$.

Fig. 2

Thin-walled circular hollow section under a linear projected force. a Elevation, b cross section, c force and projected area in a local coordinate system

To evaluate the problem above under a systematic GBT approach, the following analytical steps are performed. First, cross-sectional analysis and load’s mode participation; second, finite element solution in longitudinal direction; third and fourth, analysis of the displacement and stress fields, respectively.

Cross-sectional analysis and load’s mode participation

The cross-sectional analysis is the main feature in GBT. Usually, it leads to a quadratic eigenvalue problem, which has a non-trivial setup. However, in the case of circular hollow sections this laborious step is replaced by orthogonal deformation shapes based on Fourier series  (Schardt 1989; Silvestre 2007).³ In Fig. 3, some of these deformation shapes are presented, and their respective values are given by:

• For pure axial extension mode,

$$\begin{aligned} \quad i = a: \quad \,{}^iu\left( \theta \right) = 0 \quad \,{}^iv\left( \theta \right) = 0 \quad \,{}^iw\left( \theta \right) = 1. \end{aligned}$$

(198)

• For pure torsion mode,

$$\begin{aligned} \quad i = t: \quad \,{}^iu\left( \theta \right) = 0 \quad \,{}^iv\left( \theta \right) = 1 \quad \,{}^iw\left( \theta \right) = 0. \end{aligned}$$

(199)

• For pure longitudinal extension mode,

$$\begin{aligned} \quad i = 1: \quad \,{}^iu\left( \theta \right) = 1 \quad \,{}^iv\left( \theta \right) = 0 \quad \,{}^iw\left( \theta \right) = 0. \end{aligned}$$

(200)

• For odd modes, i = 3, 5, 7,...

$$\begin{aligned} \text { where } m = (i-1)/2 {\left\{ \begin{array}{ll} \,{}^iu\left( \theta \right) = -r\cos \left( m\theta \right) \\ \,{}^iv \left( \theta \right) = -m\sin \left( m\theta \right) \\ \,{}^iw\left( \theta \right) = m^2\cos \left( m\theta \right) \end{array}\right. }. \end{aligned}$$

(201)

• For even modes, i = 2, 4, 6,...

$$\begin{aligned} \text { where } m = i/2 \quad {\left\{ \begin{array}{ll} \,{}^iu\left( \theta \right) = r\sin \left( m\theta \right) \\ \,{}^iv\left( \theta \right) = -m\cos \left( m\theta \right) \\ \,{}^iw\left( \theta \right) = -m^2\sin \left( m\theta \right) \end{array}\right. }. \end{aligned}$$

(202)

Fig. 3

Transverse deformation shape modes of a thin-walled circular hollow section according to GBT

Once one has the functions for the orthogonal modes, it is possible to obtain the properties of the cross section. From the longitudinal displacement $\,{}^iu$, the generalized warping inertia $\,{}^iC$ is reached by adding between the membrane $\,{}^iC^M$ and the plate $\,{}^iC^P$ stiffness. This is expressed as

$$\begin{aligned} {}^iC = {}^iC^M + {}^iC^P = \oint \left( tr\,{}^iu\left( \theta \right) ^2+\frac{Kr\,{}^iw\left( \theta \right) ^2}{E}\right) {\text {d}}\theta , \end{aligned}$$

(203)

where K is the plate stiffness given by $K = \frac{E t^3}{12 \left( 1 - \mu ^2\right) }$. The inertia concerning the cross-sectional shear and Poisson effect stiffness ($\,{}^iD$ and $\,{}^iD_{\mu }$, respectively)⁴ are given by

$$\begin{aligned} \,{}^iD = \frac{r}{3}t_h^3\oint \left( \frac{\,{}^i\dot{w}\left( \theta \right) -\,{}^iv\left( \theta \right) }{r}\right) ^2 {\text {d}}\theta , \end{aligned}$$

(204)

$$\begin{aligned} \,{}^iD_{\mu } = r\oint \frac{\,{}^iw\left( \theta \right) +\,{}^i\ddot{w}\left( \theta \right) }{r^2}w\left( \theta \right) {\text {d}}\theta . \end{aligned}$$

(205)

The dot index represents the derivative $d/{\text {d}}\theta$. Finally, the distortion stiffness is given by:

$$\begin{aligned} \,{}^iB =\frac{K}{r^3}\oint \left( \,{}^iw\left( \theta \right) +\,{}^i\ddot{w}\left( \theta \right) \right) ^2{\text {d}}\theta . \end{aligned}$$

(206)

Evaluating the closed line integral from Eqs. (203) to (206), one can obtain the practical formulation:

$$\begin{aligned} \,{}^iC = {\left\{ \begin{array}{ll} 0 &{}\quad \text { for } i = t \\ 2 \pi r K/E &{}\quad \text { for } i = a \\ 2 \pi r t &{}\quad \text { for } i = 1 \\ \pi t r^3\left( 1+\frac{t^2m^4}{12r^2(1-\mu ^2)}\right) &{}\quad \text { for } i > 1 \end{array}\right. }. \end{aligned}$$

(207)

$$\begin{aligned} \,{}^iD = {\left\{ \begin{array}{ll} 0 &{}\quad \text { for } i = t \text { and } i = 1 \\ 2\pi r^3t &{}\quad \text { for } i = a \\ \pi \frac{t^3}{3 r} m^2 \left( m^2-1\right) \left( \frac{m^2}{1-\mu }-1\right) &{}\quad \text { for } i > 1 \end{array}\right. }. \end{aligned}$$

(208)

$$\begin{aligned} \,{}^iD_{\mu } = {\left\{ \begin{array}{ll} \frac{\pi }{r} m^4 \left( 1-m^2\right) &{}\quad \text { for } i > 1 \\ 0 &{}\quad \text { for all another cases }\end{array}\right. }. \end{aligned}$$

(209)

$$\begin{aligned} \,{}^iB = {\left\{ \begin{array}{ll} 0&{}\quad \text { for } i = t \text { and } i = 1 \\ 2\pi Et/r &{}\quad \text { for } i = a \\ \pi \frac{K}{r^3}m^4\left( m^2-1\right) ^2&{}\quad \text { for } i > 1 \end{array}\right. }. \end{aligned}$$

(210)

It is important to note that, from an infinite number of orthogonal deformation modes, only a few modes are necessary to evaluate an applied problem such as the one considered here. The filtering technique of the relevant deformation mode is performed by modal decomposition of the external loads, which are assumed to be represented by separation of variables:

$$\begin{aligned} p_x\left( x,\theta \right) = f_x\left( \!x\right) \! q_x \left( \!\theta \right) \end{aligned}$$

(211)

$$\begin{aligned} p_v\left( x,\theta \right) = f_v\left( \!x\right) q_v \left( \!\theta \right) , \end{aligned}$$

(212)

$$\begin{aligned} p_w\left( x,\theta \right) = f_w\left( x\right) q_w \left( \theta \right) . \end{aligned}$$

(213)

The modal decomposition is achieved by the inner product of the deformation modes  (201) and  (202), and the functions of the external load:

$$\begin{aligned} \,{}^iq_x = -r\oint q_x\left( \theta \right) \,{}^iu\left( \theta \right) {\text {d}}\theta , \end{aligned}$$

(214)

$$\begin{aligned} \,{}^iq_v = r\oint q_v\left( \theta \right) \,{}^iv\left( \theta \right) {\text {d}}\theta , \end{aligned}$$

(215)

$$\begin{aligned} \,{}^iq_w = r\oint q_w\left( \theta \right) \,{}^iw\left( \theta \right) {\text {d}}\theta . \end{aligned}$$

(216)

For instance, in the present case, the projected external load can be described in a local coordinate system (v,w) as:

$$\begin{aligned} {\left\{ \begin{array}{ll} q_v = q\sin \left( \theta \right) \cos \left( \theta \right) \\ q_w\! =\! -q\cos \left( \theta \right) ^2 \end{array}\right. } \text {for } \pi /2\! \le \! \theta \! \le \! 3\pi /2\text { and } q_x\! =\! 0. \end{aligned}$$

(217)

When these functions are applied to the inner products given in Eqs. (214),  215, and  (216), it becomes obvious which mode is relevant for the structural analysis. Moreover, inside the interval $\pi /2 \le \theta \le 3\pi /2$, all integrals of odd trigonometric functions are eliminated. Therefore, the even modes do not participate in this analysis, as $\,{}^{{\text {even}}}q_v = q m \int _{\pi /2}^{3\pi /2} \cos \left( \theta \right) \sin \left( \theta \right) \cos \left( m\theta \right) {\text {d}}\theta =0$ and $\,{}^{{\text {even}}}q_w = q m^2 \int _{\pi /2}^{3\pi /2} \cos \left( \theta \right) ^2 \sin \left( m\theta \right) {\text {d}}\theta =0$. In Table  1, a summary of the modal decomposition applied to external forces and the respective mode cross-sectional properties necessary to develop the GBT solution are presented:

Table 1 Cross section and external load modal decomposition

Here, five modes are chosen. As will be shown later, modes 3 and 5 are sufficient to solve for the displacement field. However, all modes shown above are required to obtain some particular internal forces, especially in the neighborhood of support. Further, from Table  1, it is easy to see that $^3C$ is nothing more than the moment of inertia of a traditional Euler–Bernoulli beam. For higher-order modes, 5, 7, and 11, the cross-sectional properties are unusual. Their physical meanings are related to the cross-sectional ovalization, as presented in Fig.  3. Because these high modes have extension C, shear D, distortion B, and Poisson effect stiffness $D_\mu$, the mode classification concerning the major behavior must be performed, as was shown in “Shape function assortment and the transverse deformation mode classification”.

In all GBT’s modes, distortion is the dominant behavior, which is typical in thin-walled beams. Moreover, the exact stiffness matrix approach detailed here can be applied (Table 2).

Table 2 Modal classification

Finite element solution in the longitudinal direction

After the cross-sectional properties are obtained and classified, it is possible to apply FEM to solve the longitudinal amplification for each deformation mode. Mode 3 could be solved by a well-known Hermitian element with two nodes and four degrees of freedom. However, mode 3 is solved here by a Hermitian element with three nodes and six degrees of freedom, as shown in Fig. 1. These parameters for mode 3 present an opportunity to clarify the application of the completeness coefficient matrix. For this element, the shape function vector is given by:

$$\begin{aligned} V(x) = \left[ Tx_{{\text {He}}} \right] \left[ {\text {Sh}}_{{\text {Hecc}}} \right] \left[ \vartheta \right] , \end{aligned}$$

(218)

with:

$$\begin{aligned} \left[ Tx_{{\text {He}}} \right] = \begin{bmatrix} x^5&x^4&x^3&x^2&x&1 \end{bmatrix}, \end{aligned}$$

(219)

$$\begin{aligned} \left[ \vartheta \right] = \begin{bmatrix} V_{-L/2}&V'_{-L/2}&V_{L/2}&V'_{L/2}&V_{0}&V'_{0} \end{bmatrix}^{\text {T}}. \end{aligned}$$

(220)

The completeness coefficient matrix ${\text {Sh}}_{{\text {Hecc}}}$ can be obtained by applying the procedures shown in “Inhomogeneous solution for case A with clamped–clamped boundary conditions”. For the clamped–clamped case, the result is:

$$\begin{aligned} \left[ {\text {Sh}}_{{\text {Hecc}}} \right] = \begin{bmatrix} 24\!/\!L^5&4\!/\!L^4&-24\!/\!L^5&4\!/\!L^4&0&16\!/\!L^4 \\ -8\!/\!L^4&-2\!/\!L^3&-8\!/\!L^4&2\!/\!L^3&16\!/\!L^4&0 \\ -10\!/\!L^3&-1\!/\!L^2&10\!/\!L^3&-1\!/\!L^2&0&-8\!/\!L^2 \\ 4\!/\!L^2&1\!/\!(2L)&4\!/\!L^2&-1\!/\!(2L)&-8\!/\!L^2&0 \\ 0&0&0&0&0&1 \\ 0&0&0&0&1&0 \end{bmatrix} \end{aligned}$$

(221)

The corresponding kernel stiffness matrix and force vector (for linear external force: $f=ax+b$) for this case are, respectively:

$$\begin{aligned} \left[ \Upsilon ''_{{\text {He}}} \right] = \begin{bmatrix} 25L^7/28&0&3L^5/2&0&0&0\\&9L^5/5&0&2L^3&0&0 \\&&3L^3&0&0&0\\&&&4L&0&0\\&&&&0&0\\ {\text {Sym.}}&&&&&0 \end{bmatrix} \end{aligned}$$

(222)

$$\begin{aligned} \left[ F_{{\text {He}}} \right] = \begin{bmatrix} \frac{aL^7}{448}&\frac{bL^5}{80}&\frac{aL^5}{80}&\frac{bL^3}{12}&\frac{aL^3}{12}&bL \end{bmatrix}^{\text {T}}. \end{aligned}$$

(223)

Now, one can build the effective stiffness matrix by applying the transformation of the completeness coefficient matrix: $\,{}^3\left[ K_c \right] = E\,{}^3C \,{}^3\left[ {\text {Sh}}_{{\text {Hecc}}} \right] ^{\text {T}} \,{}^3\left[ \Upsilon _{He}'' \right] \,{}^3\left[ {\text {Sh}}_{{\text {Hecc}}} \right]$, and the effective external force vector:

$$\begin{aligned} \left[ {}^3F \right] =\,{}^3\left[ {\text {Sh}}_{{\text {Hecc}}} \right] ^{\text {T}} \left[ F_{{\text {He}}} \right] . \end{aligned}$$

Together with the boundary conditions of the null displacement and rotation in $x=-L/2$, the system of equations for the nodal displacements in mode 3 (units in N and mm) are:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {1.69e + 4} \\ { - 3.21e + 7} \\ {2.4e + 4} \\ {5.14e + 7} \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} {4.39e + 3} & { - 2.94e + 7} & { - 3.09e + 3} & { - 4.97e + 7} \\ {} & {2.58e + 11} & {2.32e + 7} & {2.48e + 11} \\ {} & {6.18e + 3} & 0 & {} \\ {{\text{Sym}}} & {} & {9.94e + 11} & {} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mkern 1mu} ^{3} V_{{L/2}} } \\ {{\mkern 1mu} ^{3} V^{\prime}_{{L/2}} } \\ {{\mkern 1mu} ^{3} V_{0} } \\ {{\mkern 1mu} ^{3} V^{\prime}_{0} } \\ \end{array} } \right] \\ \therefore {\mkern 1mu} \left[ {\begin{array}{*{20}c} {{\mkern 1mu} ^{3} V_{{L/2}} } \\ {{\mkern 1mu} ^{3} V^{\prime}_{{L/2}} } \\ {{\mkern 1mu} ^{3} V_{0} } \\ {{\mkern 1mu} ^{3} V^{\prime}_{0} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} {273.28} \\ {0.0124} \\ {93.94} \\ {0.0106} \\ \end{array} } \right]. \\ \end{aligned}$$

(224)

With the nodal displacement values, one can obtain the displacement field corresponding to mode 3 at any position in the longitudinal direction by Eq. (218) and its first derivative. Up to this point the present solution leads to the well-known Bernoulli–Euler beam model, which cannot reveal any cross-sectional distortion or warping. At this point, GBT rises as an extension of this traditional beam model and provides these cross-sectional deformations. In this sequence, it the FEM analysis is developed for the higher-order GBT modes 5, 7, and 11:

• mode 5: To build up the completeness coefficient and stiffness matrices, one must first find the values of $\alpha$ and $\beta$:

$$\begin{aligned} \,{}^5\alpha = \sqrt{\sqrt{\frac{B}{4EC}}+\frac{\overline{GD}}{4EC}} = 0.000113855, \end{aligned}$$

(225)

$$\begin{aligned} \,{}^5\beta = \sqrt{\sqrt{\frac{B}{4EC}}-\frac{\overline{GD}}{4EC}} = 0.000113401. \end{aligned}$$

(226)

Next, the completeness coefficient matrix is evaluated based on the clamped–clamped boundary conditions Eq. (45):

$$\begin{aligned} \left[ {\text {Sh}}_{\text {NHacc}} \right] = \left[ {\begin{matrix} 0.25 &{} 2,341.167 &{} 0.25 &{}-2,341.167 &{} -0.5 &{} 0.0 \\ -1.071 &{} -4,823.949 &{} 1.071 &{} -4,823.949 &{} 0.0 &{} -22,473.151 \\ 0.318 &{} 1,212.475 &{} 0.318 &{} -1,212.475 &{} -0.637 &{} 0.0 \\ -0.342 &{} -2,639.382 &{} 0.342 &{} -2,639.382 &{} 0.0 &{} -4,994.045\\ 0.00016 &{} 0.848 &{} -0.00016 &{} 0.848 &{} 0.0 &{} 4.117\\ -0.25 &{} -2,341.167 &{}-0.25 &{} 2,341.167 &{} 1.5 &{} 0.0 \end{matrix}}\right] . \end{aligned}$$

(227)

Following the presented procedure, the kernel stiffness matrices due to longitudinal stress, transverse shear, and distortion are addressed by their respective Eq. (112):

$$\begin{aligned} \left[ \Upsilon _{\text {NHa}}'' \right] \! = \! 10^{-11} \begin{bmatrix} 3.048&0&-0.794&0&0&0 \\&0.403&0&-0.802&0&0 \\&&1.327&0&0&0 \\&&&4.124&0&0 \\&&&&0&0 \\ {\text {Sym }}&&&&&0 \end{bmatrix}. \end{aligned}$$

(228)

$$\begin{aligned} \left[ \Upsilon _{\text {NHa}}' \right] = 10^{-4} \begin{bmatrix} 5.69&0&-7.218&0&0&0 \\&11.534&0&-3.344&56.499e\!+3&0 \\&&11.843&0&0&0 \\&&&5.412&-6.928e\!+3&0 \\&&&&3e\!+8&0 \\ {\text {Sym }}&&&&&0 \end{bmatrix}. \end{aligned}$$

(229)

$$\begin{aligned} \left[ \Upsilon _{{\text {Ha}}} \right] = 10^{4} \begin{bmatrix} 1.9814&0&1.1803&0&0&2.1757 \\&6.1946&0&1.1803&3.709e\!+4&0\\&&4.5811&0&0&2.7954 \\&&&0.5949&8.088e\!+3&0 \\&&&&2.25e\!+8&0 \\ {\text {Sym}}&&&&&3.0 \end{bmatrix}. \end{aligned}$$

(230)

$$\begin{aligned} \left[ \Upsilon _{{\text {Ha}}}'',' \right] = 10^{-4} \begin{bmatrix} -6.036&0&-6.682&0&0&-7.198 \\&6.143&0&-14.43&2.103+4&0 \\&&6.122&0&0&5.627 \\&&&-6.054&-9.567+4&0 \\&&&&0&0 \\ {\text {Sym}}&&&&&0 \end{bmatrix}. \end{aligned}$$

(231)

From Eq. (113), these matrices lead to the exact stiffness matrix, which are presented below in Eq. (232). The corresponding load vector is obtained from Eq. (115):

$$\begin{aligned} \,{}^5[K_{\text {NHa}}] = 10^{3} \left[ {\begin{matrix} 6.957 &{} 3.394e\!+4&{} -1.022&{} 5.219e\!+3&{} -2.216&{} 4.563e\!+4\\ &{} 2.679e\!+8&{} -5.219e\!+3&{} 2.587e\!+7&{} -2.076e\!+4&{} 2.411e\!+8\\ &{} &{} 6.957&{} -3.394e\!+4&{} -2.216&{} -4.563e\!+4\\ &{} &{} &{} 2.679e\!+8&{} 2.076e\!+4&{} 2.411e\!+8\\ &{} &{} &{} &{} 1.330e\!+1&{} 0\\ Sym&{} &{} &{} &{} &{} 1.171e\!+9 \end{matrix}}\right] \end{aligned}$$

(232)

,

$$\begin{aligned}{\mkern 1mu} ^{5} \left[ {F_{{{\text{NHacc}}}} } \right]^{{\text{T}}} = 10^{4} \left[ {\begin{array}{*{20}c} { - 0.91} & { - 2.9e + 3} & { - 3.92} & {7.42e + 3} & { - 5.77} & { - 12.33e + 3} \\ \end{array} } \right].\end{aligned}$$

(233)

The boundary conditions for GBT’s higher-order modes are, in this case, the same as those in Euler–Bernoulli bending, as the longitudinal (warping) and transverse (distortion) at the initial point $x=-L/2$ are restrained. After this restriction, one can solve the system of linear equations to determine the other degrees of freedom:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} { - 3.9246} \\ {7.416e + 3} \\ { - 5.7668} \\ { - 12.335e + 3} \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} {6.957e - 1} & { - 3.394e + 3} & { - 2.216e - 1} & { - 4.563e + 3} \\ {} & {2.679e + 7} & {2.076e + 3} & {2.411 + 7} \\ {} & {} & {1.33} & 0 \\ {{\text{Sym}}} & {} & {} & {1.171e + 8} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mkern 1mu} ^{5} V_{{L/2}} } \\ {{\mkern 1mu} ^{5} V^{\prime}_{{L/2}} } \\ {{\mkern 1mu} ^{5} V_{0} } \\ {{\mkern 1mu} ^{5} V^{\prime}_{0} } \\ \end{array} } \right] \\ \therefore {\mkern 1mu} \left[ {\begin{array}{*{20}c} {{\mkern 1mu} ^{5} V_{{L/2}} } \\ {{\mkern 1mu} ^{5} V^{\prime}_{{L/2}} } \\ {{\mkern 1mu} ^{5} V_{0} } \\ {{\mkern 1mu} ^{5} V^{\prime}_{0} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} { - 13.303} \\ { - 4.896e - 4} \\ {5.788} \\ { - 5.228e - 4} \\ \end{array} } \right]. \\ \end{aligned}$$

(234)

• modes 7, 11, and axial: The approach for these modes follows the same as that used for mode 5. Therefore, here only the final values of nodal displacements are presented:

$$\begin{aligned} \,{}^a\left[ \vartheta \right] ^{\text {T}}= \begin{bmatrix} 0.0&0.0&-4.573e\!-\!4&-1.524e\!-\!8&-2.287e\!-\!4&-1.524e\!-\!8 \end{bmatrix}, \end{aligned}$$

(235)

$$\begin{aligned} \,{}^7\left[ \vartheta \right] ^{\text {T}}= \begin{bmatrix} 0.0&0.0&2.763-1&9.547-6&1.384-1&9.152-6 \end{bmatrix}, \end{aligned}$$

(236)

$$\begin{aligned} \,{}^{11}\left[ \vartheta \right] ^{\text {T}}= \begin{bmatrix} 0.0&0.0&-1.59-3&-7.24-8&-7.88-4&-5.26-8 \end{bmatrix}. \end{aligned}$$

(237)

In the case of the axial mode, there is no torsion stiffness ($D=0$), which leads to the particular case $\alpha = \beta$.

Analysis of the displacement field

Here, the generalized displacement and rotation functions are plotted, and these functions are compared with the solution obtained from the usual Hermitian shape functions (2 nodes and 4 degrees of freedom). Moreover, the detailed cross-sectional transverse deformation at the extreme free point of the structure is shown. This cross-sectional deformation is compared with the results obtained from FEM analysis based on the shell elements.

The generalized displacement functions given by Eq.  (62), which provide amplification to the GBT modes for transverse deformation, are plotted below for modes a, 5, 7, and 11 in Figs. 4, 5, 6, and 7, respectively. The amplification functions for cross-sectional warping, i.e., the longitudinal displacement, are found by the first derivative of Eq. (62) and are plotted below for the same modes in Figs. 8, 9, 10, and 11, respectively.

Fig. 4

Generalized displacement of the axial mode, $\,{}^aV$ (in mm)

Fig. 5

Generalized displacement of mode 5, $\,{}^5V$ (in mm)

Fig. 6

Generalized displacement of mode 7, $\,{}^7V$ (in mm)

Fig. 7

Generalized displacement of mode 11, $\,{}^{11}V$ (in mm)

Fig. 8

Generalized warping displacement of the axial mode, $\,{}^aV'$ (in m/m)

Fig. 9

Generalized warping displacement of mode 5, $\,{}^5V'$ (in m/m)

Fig. 10

Generalized warping displacement of mode 7, $\,{}^7V'$ (in m/m)

Fig. 11

Generalized warping displacement of mode 11, $\,{}^{11}V'$ (in m/m)

One can observe that the solution obtained from a single Hermitian element lacks precision, which can be overcome by finer discretization, e.g., with ten elements as used above. Although this solution seems to have better accuracy for the displacement field concerning the lower-order modes 5 and 7, the first derivatives for the higher modes, such as 11 and the axial mode, near the support boundary condition have coarse results. Further, it is important to keep in mind that this solution was obtained from a linear equation system of 20 unknowns instead of a system with 4 unknowns, as proposed here by the trigonometric–hyperbolic shape functions. Moreover, the high computational performance of GBT is only reached by coarse longitudinal beam discretization. If some structural analysis requires many GBT modes, it will lead to similar amount of degrees of freedom for each beam node as in the case of a cross section modeled by shell elements. This GBT model with a high number of modes, together with fine longitudinal discretization, provides a total number of unknowns that is similar to a traditional shell element analysis. This case is especially applicable in non-linear analysis involving plasticity  (Abambres et al. 2013).

Actually, shell element models with high discretization are used in the approach to validate the GBT’s models, which are based on comparison of the results from both types of models  (Silvestre and Gardner 2011; Silvestre et al. 2012; Martins et al. 2017).

Here, the results using shell elements were obtained from commercial ANSYS^® software, where four models based on shell elements types 63, 93, 181, and 281 were developed. The discretization among these models are the same: 100 nodes for the cross section and 600 element segments in the longitudinal direction. This leads to a total of 60,000 elements. The difference among these models is the type of interpolation function applied: linear (shell-63 and shell-181) or quadratic (shell-93 and shell-281). These elements are based on one of the follow kinematic hypotheses: Kirchhoff–Love (shell-63 and shell-93) and Mindlin–Reissner (shell-181 and shell-281).

A comparison of the displacement fields between the models is conducted in the cross section at the free extreme, which is plotted in Figs. 12 and  13. The transverse deformation obtained from GBT is achieved by a combination of radial and tangential displacements v and w,  respectively, which are given by the summation of all n modal participation factors:

$$\begin{aligned} w\left( x,\theta \right) = \sum _{i=1}^{n} \,{}^iV\left( x\right) \,{}^iw\left( \theta \right) +\mu \frac{r^2}{{}^im^2}\,{}^iV''\left( x\right) \,{}^iw\left( \theta \right) , \end{aligned}$$

(238)

$$\begin{aligned} v\left( x,\theta \right) = \sum _{i=1}^{n} \,{}^iV\left( x\right) \,{}^iv\left( \theta \right) . \end{aligned}$$

(239)

Here, the second term in Eq. (238) was added into the formulation of  Schardt (1989) and  Silvestre (2007) to represent the Poisson effect in the membrane behavior. It only affects the displacement field. The values of $\,{}^iV\left( x\right)$ and $\,{}^iV''\left( x\right)$ for each mode are taken at node $x=L/2$, and for each desired point on this cross section, the values $v\left( \theta \right)$ and $w\left( \theta \right)$ are accessed in Eq. (201).

Fig. 12

Results of top cross-sectional deformation. The GBT solution is obtained by the summation of all modal deformation factors. The solution achieved from shell elements is also presented

Fig. 13

Longitudinal displacement results at the top cross section: comparison between the solutions of GBT and shell elements

One can note in Fig. 12 that the contribution from modes 7, 11, and axial are almost undetectable in the total displacement. Nevertheless, these modes are required to achieve an accurate stress field, as shown in the next subsection. Table  3 shows that the highest mean difference is around $0.8\%$, which occurs in the tangential direction v between GBT and Shell-63. Further, it shows that the GBT results approach the response of elements with quadratic interpolation functions (Shell-93 and Shell-281).

Table 3 Mean differences (%) and standard deviation (SD) of the displacement field between the GBT and shell element models

For longitudinal displacement, the differences are even smaller. The highest mean difference is around 0.16% with respect to Shell-181. Figure 13 presents a diagram of the longitudinal displacement to illustrate the quality of the results:

Analysis of the stress field

In GBT, the longitudinal and shear stresses at a particular point of one cross section are easily given by the summation among all stress modal participation factors, which are a generalization of the stresses from Bernoulli–Euler beam theory:

$$\begin{aligned} \sigma _x\left( x,\theta \right) = \sum _{i=1}^{n} \frac{\,{}^iW\left( x\right) \,{}^iu\left( \theta \right) }{\,{}^iC}, \end{aligned}$$

(240)

$$\begin{aligned} \tau _x\left( x,\theta \right) = \sum _{i=1}^{n} \frac{\,{}^iW'\left( x\right) \,{}^iS\left( \theta \right) }{\,{}^iC}, \end{aligned}$$

(241)

$\,{}^iS\left( \theta \right) =\int _{0}^{s}\,{}^iu\left( \theta \right) {\text {d}}s$ is the generalized first moment. $\,{}^iW\left( x\right)$ and $\,{}^iW'\left( x\right)$ are the generalized bending moments and shear forces, respectively, and are given by:

$$\begin{aligned} \,{}^iWx\left( x\right) = E \,{}^iC \,{}^iV''\left( x\right) , \end{aligned}$$

(242)

$$\begin{aligned} \,{}^iW'x\left( x\right) = E \,{}^iC \,{}^iV'''\left( x\right) . \end{aligned}$$

(243)

Similar to the displacement field, the results from the stress field are plotted from the present formulation of the exact GBT solution and the traditional Hermitian shape functions.

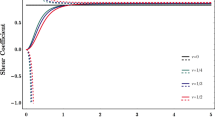
The stress field results found from Hermitian and trigonometric–hyperbolic functions have a clear contrast. Due to the higher-order derivatives required to achieve the stress fields, the Hermitian shape functions present discontinuities, especially for the generalized shear force (see Figs. 14, 15, 16,  17, 18, 19, 20 and 21). Because trigonometric–hyperbolic shape functions always have derivatives, such an effect does not exist. Besides, the generalized bending moments for axial and higher order modes (Figs.  14, 18, respectively) present an exponential growing behavior near the support. Consequently, the Hermitian shape functions require an even higher discretization in this domain.

Fig. 14

Generalized internal force of the axial mode, $\,{}^aW$ (in kN m)

Fig. 15

Generalized internal force of the axial mode, $\,{}^aW'$ (in kN)

Fig. 16

Generalized internal force of mode 5, $\,{}^5W$ (in kN m)

Fig. 17

Generalized internal force of mode 5, $\,{}^5W'$ (in kN)

Fig. 18

Generalized internal force of mode 7, $\,{}^7W$ (in kN m)

Fig. 19

Generalized internal force of mode 7, $\,{}^7W'$ (in kN)

Fig. 20

Generalized internal force of mode 11, $\,{}^{11}W$ (in kN m)

Fig. 21

Generalized internal force of mode 11, $\,{}^{11}W'$ (in kN)

This issue of precision deficiency in the Hermitian shape function has a particular highlight in the case of circular hollow sections, whose internal forces are obtained from a combination of the higher order derivatives. For instance, the bending moments of the plate for this cross section are given by  Silvestre (2007) and Schardt (1989)⁵:

$$\begin{aligned} M_x\left( \!x\!,\!s\!\right) = - \, K \sum _{i=2}^{n} {}^iw\left( \theta \right) {}^iV''\left( \!x\!\right) \!+\!\mu \frac{{}^iw\left( \theta \right) \!+\!{}^i\ddot{w}\left( \theta \right) }{r^2}{}^iV\left( \!x\!\right) , \end{aligned}$$

(244)

$$\begin{aligned} M_\theta \left( x,\theta \right) =- \, K \sum _{i=2}^{n} \frac{\,{}^iw\left( \theta \right) +\,{}^i\ddot{w}\left( \theta \right) }{r^2}\,{}^iV\left( x\right) \end{aligned}$$

(245)

$$\begin{aligned} M_{x\theta }\left( x,\theta \right) = - \, K\frac{1-\mu }{r} \sum _{i=2}^{n} \left( {}^i\dot{w}\left( \theta \right) -{}^iv\left( \theta \right) \right) \,{}^iV'\left( x\right) , \end{aligned}$$

(246)

$$\begin{aligned} Q_x\left( x,\theta \right)&= - \, K \sum _{i=1}^{n} \,{}^iw\left( \theta \right) \,{}^iV'''\left( x\right) \nonumber \\&\quad +\left( \mu \left( \,{}^iw\left( \theta \right) +\,{}^i\dot{v}\left( \theta \right) \right) +{}^i\ddot{w}\left( \theta \right) -\,{}^i\dot{v}\left( \theta \right) \right) \frac{\,{}^iV'\left( x\right) }{r^2}, \end{aligned}$$

(247)

$$\begin{aligned} Q_\theta \left( x,\theta \right)&= \frac{K}{r} \sum _{i=1}^{n} \left( 1-\mu \right) \left( {}^i\dot{w}\left( \theta \right) -{}^iv\left( \theta \right) \right) {}^iV''\left( x\right) \nonumber \\&\quad +\frac{\,{}^i\dddot{w}\left( \theta \right) +\,{}^i\dot{w}\left( \theta \right) }{r^2}\,{}^iV\left( x\right) . \end{aligned}$$

(248)

To illustrate the quality of the results obtained from the presented GBT approach, all internal bending moments and shear forces in the cross section at the point $x=1$ m are plotted below alongside the results obtained from shell element models.

Figures  22, 23, 24, 25 and  26 show how GBT approaches the results of the other models. It also indicates that there is no consensus among the different shell element models regarding the values of the plate’s internal forces. Tables  4, 5, 6, 7 and  8 present mean differences and standard deviations for all models.

Fig. 22

Longitudinal bending moment $M_x$ at $x=1$ m for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from the shell element models

Fig. 23

Transverse bending moment $M_\theta$ at $x=1$ m for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from the shell element models

Fig. 24

Twist bending moment $M_{\theta x}$ at $x=1$ m for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from the shell element models

Fig. 25

Longitudinal shear forces $Q_x$ at $x=1$ m for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from shell element models

Fig. 26

Transverse shear forces $Q_x$ at $x=1$ m for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from the shell element models

Table 4 $M_x$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

Table 5 $M_\theta$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

Table 6 $M_{\theta x}$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

Table 7 $Q_{x}$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

Table 8 $Q_{\theta }$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

The membrane’s internal forces can be also presented in the GBT modal composition, but in the case of these internal forces even higher-order derivatives are required (Silvestre 2007; Schardt 1989):

$$\begin{aligned} N_x\left( x,\theta \right) = Et\sum _{i=1}^{n} \,{}^iV''\left( x\right) \,{}^iu\left( \theta \right) , \end{aligned}$$

(249)

$$\begin{aligned} N_{\theta x}\left( \!x\!,\theta \!\right) = N_{\theta x}^{\text {T}}\! +\! r\!\sum _{i=2}^{n} \left( \!Et{}^iV'''\left( x\right) \! -\! \frac{\,{}^iq_xf_x\left( x\right) }{\pi r^3} \right) \frac{\,{}^i\dot{u}\left( \theta \right) }{m^2}, \end{aligned}$$

(250)

$$\begin{aligned} N_{\theta }\left( x,\theta \right) &= N_{\theta }^A + r f_w\left( x\right) q_w \left( \theta \right) \nonumber \\ &\quad -K\sum _{i=2}^{n}r\,{}^iw\left( \theta \right) \,{}^iV''''\left( x\right) +\frac{\,{}^i\ddddot{w}\left( \theta \right) +\,{}^i\ddot{w}\left( \theta \right) }{r^3}\,{}^iV\left( x\right) \nonumber \\ &\quad+ \left( \mu \left( {}^iw\left( \!\theta \!\right) -{}^i\ddot{w}\left( \!\theta \!\right) \right) +2\left( {}^i\dot{v}\left( \!\theta \!\right) \left( \mu -1\right) +{}^i\ddot{w}\left( \!\theta \!\right) \right) \right) \frac{\,{}^iV''\left( \!x\!\right) }{r}. \end{aligned}$$

(251)

Here, the constants $N_{\theta x}^{\text {T}}$ and $N_{\theta }^A$ are the shear from the uniform torsion mode and the tangential force due to the axial mode, respectively  (Silvestre 2007).

In particular, the membrane force in the axial direction $N_\theta$ requires a fourth-order derivative, which is eliminated in the traditional Hermitian shape functions. This is another point that stresses the need for functions with continuous derivatives, such as the hyperbolic–trigonometric functions presented here.

Figures  27, 28 and  29 illustrate how all models converge to nearly the same internal force of the membrane. Tables  9, 10 and 11 quantify the mean differences and standard deviations for all models.

Fig. 27

Longitudinal membrane force $N_x$ at $x=1$ m of for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from the shell element models

Fig. 28

Transverse membrane force $N_\theta$ at $x=1$ m of for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from the shell element models

Fig. 29

Membrane shear force $N_{\theta x}$ at $x=1$ m of for the GBT modes. The final result, which is a summation over all modes, is plotted together with the results obtained from shell element models

Table 9 $N_x$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

Table 10 $N_\theta$: mean differences (in table’s upper-right side) and standard deviations (in table’s lower-left side) for all models

Table 11 $N_{\theta x}$: mean differences (in table’s upper-right side), and standard deviations (in table’s lower-left side) for all models

Conclusion

This work presented the procedure and results for calculating the exact stiffness matrices in GBT. Based on the various possible solutions of the inhomogeneous differential equation for GBT, the choice of the exact stiffness matrix is guided by the classification of each warping mode as either dominant distortion, dominant torsion, or critical distortion–torsion.

In the Euler–Bernoulli beam finite element, the loading function can usually be described as a linear combination of shape functions, i.e., a constant or linearly distributed load can be expressed by a linear combination of Hermitian functions. However, in GBT, the shape functions based on the exact solution of the homogeneous differential equation lead to a combination between trigonometric and hyper-trigonometric functions, which are linearly independent with respect to constant, linear, or other polynomial functions. Therefore, the exact solution for a GBT element must be based not only on the homogeneous differential equation, but it must also account for the particular solution, which will increase the number of nodes in the beam element.

To overcome the complexity in the stiffness matrix, it is split into a kernel stiffness matrix under a transformation via the completeness coefficient matrix. This matrix not only enables one to handle complex and long shape functions, but can also provide a systematic approach, in which the element boundary conditions can be easily managed.

The numerical example shows the benefits of using the exact stiffness matrix. First, the exact solution is obtained without extra effort due to longitudinal discretization of the element. Consequently, the number of unknowns in finite element analysis is reduced. Second, the displacement and stress fields (in particular, the generalized shear internal force) are obtained without applying any perturbation to the approximate solution. On the other hand, the implementation of the stiffness matrix in GBT involves terms which are much more complex than the usual terms in the stiffness matrix based on Hermitian shape functions. Furthermore, the numerical example shows how GBT and the different types of shell element models lead to the almost same displacement field and internal forces of the membrane. Without the same precision, all models approach to the approximated results for the internal forces of the plate.