Introduction

The potential of CNT nanocomposites in mechanical, electrical, electronic and several other applications is nowadays undeniable (Thostenson et al. 2001; Li et al. 2008). Macroscopic forms of CNTs, such as arrays, yarns, fibers and films, have been reported and made the macroscopic manipulation of CNTs feasible for broad applications (Fan et al. 1999; Vigolo et al. 2000; Hata et al. 2004; Xi and Pei 2007; Zhang et al. 2006; Dharap et al. 2004; Yao et al. 2006; Hone et al. 2000; Itkis et al. 2007; Kaw 2005; An et al. 2012; Ci et al. 2005; Jiang et al. 2002; Qu et al. 2006).

It is expensive and difficult to evaluate the effective properties of composites through experiments. This issue has made researchers introduce analytical models and methods to predict these properties. In 1929, rule of mixture was offered as the simplest and well-known micro-mechanical model for determination of the composites properties (Kaw 2005) and, so far, other varying models have also been introduced that each of them has its own cons and pros. Ji et al. (2004) proposed a revised formula for the “rule of mixture” which was named as the “generalized mixture rule (GMR)”. Younes et al. (2012), while reviewing well-known micromechanical models, obtained the elastic properties of various composites with the use of eight models and compared them with FEM and experimental results.

Many researches have been recently done about the effect of SWCNTs and MWCNTs on the mechanical properties and vibrational response of structures (Ayatollahi et al. 2015; Taraghi et al. 2014; Bakhti et al. 2013; Jahangiri et al. 2015; Park and Yoo 2013, 2015; Tagrara et al. 2015), it shows that the development of nanocomposites has become an attractive new subject in materials science.

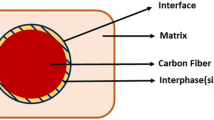
Representative volume element (RVE) is a statistical sample of all the material properties in a way that the desired material is created by the infinite stacking of these elements. RVE can show the real stress and strain of a material and offers a good understanding of its elastic properties. Considerable efforts have been made to determine the elastic properties of nanocomposites using finite element modeling (FEM) (Alexander and Tzeng 1997; Robertson et al. 1992; Lu 1997a, b). A method for investigating the mechanical response of heterogeneous materials with embedded circular inclusions was demonstrated by Liu and Chiou (2004). The effects of varying the elastic modulus and thickness of the interphase and its effective modulus were analyzed using the commercial software ABAQUS. They found, as might be expected, that the effective elastic modulus depends on the shape and orientation of the inclusions. Moreover, it was found that increasing the interphase thickness would lead to an increase in the effective modulus.

Chen and Liu (2004) simulation represents the effect of elastic modulus and Poisson’s ratios in the transverse plane, using a square matrix with multiple carbon nanotubes. According to their FEM results, as the carbon nanotube volume fraction increased by 3.6 %, the stiffness of composite rises to 33 %. In addition, Xia et al. (2004) have modeled toughening mechanisms in carbon nanotubes ceramic matrix composites.

The exceptional mechanical properties of CNT, such as hardness, high strength and flexibility, low density and excellent electrical and thermal properties, have made it an ideal reinforcement for use in composites. It has been observed that the addition of 1 wt% (i.e., 1 % by weight) CNT to a matrix resulted in 36–42 % increases in the composite hardness (Thostenson et al. 2005). Schadler et al. (1998) have shown that with increasing 5 % volume fraction of CNT to epoxy matrix, its strength has been increased up to 40 % compared to pure epoxy matrix. Liu and Chen (2003) have investigated the mechanical effect of CNT in polymer with the help of RVE and 3D FE analysis. Namilae and Chandra (2005) performed a multi-scale study to investigate the effect of CNT on polymer and the phase interface. All of these studies show that the use of CNT in materials can make them highly strong.

The most commonly used computational method for designing nanomaterials has been the atomistic approach, including the classical molecular dynamics and ab initio techniques (Robertson et al. 1992; Halicioglu 1998; Tersoff 1988; Brenner 1990; Lu 1997a, b; Overney et al. 1993; Popov and Van Doren 2000; Hernandez et al. 1999; Sanchez-Portal et al. 1999; Van Lier et al. 2000). The molecular simulations often require huge computational resources and are limited to simulating 106–108 atoms for a few nanoseconds (Qian et al. 2002; Wang and Wang 2004; Wang et al. 2011). Therefore, although the atomistic method has been very successful for modeling an individual nanotube, it would not be a feasible approach for modeling the nanotube arrays. Structural mechanics techniques, e.g., the discrete beam elements, have gained popularity recently due to their abilities to handle larger size CNT models. Wang et al. (2011) have modeled vertically aligned, single-walled CNT arrays (VA-SWCNTs) by treating individual tubes in the arrays as 1D solid rods.

Despite the aforementioned extensive research on determination of mechanical properties of Nano composites reinforced with CNTs, to the authors’ best knowledge, very little work has been done in the open literature for analyzing the mechanical properties of radical aligned carbon nanotubes (RA-CNTs), and most of previous works deal with the determination of mechanical properties of vertically align carbon nanotubes (VA-CNTs). This study is carried out in two ways. Firstly, the effect of microfiber as reinforcement on the effective material properties is investigated; secondly, the study is carried on as the microfibers reinforced by CNT arrays. In both the above-mentioned approaches, the results are compared with the results of Generalized Mixture Rule (GMR) which is known as a widely used micro-mechanical model. The Representative Volume Element (RVE) is considered as a well-known method to investigate the effect of adding CNT arrays on the skin of microfibers. The results show that Generalized Mixture Rule cannot properly predict the effects of changing the length and diameter of nanotubes on the effective properties of nanocomposites.

Problem description

Researchers have used modern methods to develop CNT on different surfaces as depicted in Figs. 1 and 2.

Fig. 1
figure 1

A photo sample of nanotubes created on the surface of a fiber (the scale of the photos is 5 μm) (Qu et al. 2006)

Full size image
Fig. 2
figure 2

A photo of SiC fibers with carbon fiber skin (Ci et al. 2005)

Full size image

The main purposes of this research are to specify the effect of changing the volume fraction, length, diameter and the size of nanotubes on longitudinal, transverse Young’s Modulus, Poisson ratio and pull-out forces of composites. In this study, the RVE model is used to investigate the effects of all the above-mentioned parameters on material properties of composite. A 3D view of the desired RVE is given in the following (Fig. 3). Due to the existence of many nanotubes, the analysis of such a 3D RVE will be time taking. To reduce the time of calculation, this element is considered as a 2D RVE model which is shown in Fig. 4.

Fig. 3
figure 3

A 3D model of a fiber reinforced by CNTs array

Full size image
Fig. 4
figure 4

A 2D RVE with CNTs on the surface of fibers

Full size image

As an initial assumption, the fiber diameter is considered 10 µm; the fiber volume percent and the wall thickness of the nanotube are considered to be 0.4 and 34 nm, respectively. By considering these values and with the use of proportions, one can get the matrix dimensions (length and height). The properties of RVE, including matrix, fibers and nanotubes are given in Table 1 (Feng et al. 2011; Jones 1998).

Table 1 The material properties of RVE components
Full size table

Micromechanical modeling

Predicting the mechanical properties of composites has been the main objective of many researches, and various micromechanical models have been proposed to determine their elastic properties. These models can be categorized into four major categories, including classic models, models with elastic approach, semi-experimental models and homogenous models; in the following, some of the most well-known models are introduced.

Rule of mixture is the most common theoretical model used for the estimation of the mechanical properties of a material consisting of matrix and continuous fiber; this rule is proposed by Voigt and Reuss (Kaw 2005). In this model, the deformation of fibers and matrix is studied individually, and the resulting longitudinal deformation caused by transverse loading will not be considered. This hypothesis is fairly simple and its results have a good agreement with experimental and FE data; but some correction coefficients have been added to this formula to reduce error, and the resulting formula has been presented with the name of modified rule of mixture. Hashin and Rosen (1964) have proposed composite cylinder assemblage model for the calculation of composite elastic properties. Halpin–Tsai model (Halpin and Kardos 1976; Affdl and Kardos 1976) is a semi-empirical model proposed for the correction of transverse and shear modulus. Chamis model (1989) has provided a series of equations for four independent constants of an orthotropic material. A relatively new model called bridging micromechanics model has been also offered by Huang (2001) which has been generalized to predict the strength of unidirectional composites.

By generalized mixture rule (GMR) for a composite consisting of three components including matrix, fibers and nanotubes, it is possible to write the longitudinal, transverse Young’s modulus and Poisson’s ratio in the following form:

$$E_{1} = E_{m} V_{m} + E_{f} V_{f} + E_{c} V_{c}$$
(1)
$$\frac{1}{{E_{2} }} = \frac{{V_{m} }}{{E_{m} }} + \frac{{V_{f} }}{{E_{f} }} + \frac{{V_{c} }}{{E_{c} }}$$
(2)
$$\upsilon_{12} = \upsilon_{m} V_{m} + \upsilon_{f} V_{f} + \upsilon_{c} V_{c}$$
(3)

where subscripts “m”, “f” and “c” refer to matrix, fiber and nanotube, respectively.

Although the dimensions and size of the composite components have significant effects on the modulus or Poisson’s coefficient, they have not considered in the rule of mixture theory. So, the effect of nanotube length and diameter on these properties is investigated using ABAQUS software to assess this issue.

FE modeling in ABAQUS

In this stage, first the RVE which includes the matrix and microfibers will be modeled and analyzed without adding any nanotubes. In the next stages, once the nanotubes with different length, diameter and volume percent are added, the analysis continues. The RVE is considered as a clamped-free structure, then the axial displacement (1 µm) is applied to the free edge of structure as shown in Fig. 5.

Fig. 5
figure 5

A 2D RVE with its boundary conditions

Full size image

Using Hooke’s law for the beam, the RVE Young’s modulus can be calculated as follows:

$$\delta = \frac{Fl}{AE} \to E = \frac{Fl}{A\delta }$$
(4)

In Eq. 4, L is the initial length of RVE in displacement direction, A is the cross-section area, E is the Young’s modulus in the displacement direction, and F is the force created in the nodes at the beginning or end of the section which is calculated by software. By knowing L, A, displacement and calculating F using ABAQUS software, the value of E in that direction will be obtained. We repeat these stages for the other two edges of the RVE to also obtain the Young’s modulus for that direction. To calculate the amount of Poisson’s ratio, the following equation could be used:

$$\upsilon_{12} = - \frac{{\varepsilon_{2} }}{{\varepsilon_{1} }}$$
(5)

Another method which is used to investigate the effect of adding nanotubes on composite strength is “pull-out force”. To do this, from one side, the matrix is kept fixed and from the other side, the microfibers are pulled out from the RVE. It is expected that after the addition of nanotubes, this force increases.

The size and shape of the meshes have a great effect on the results. Generally, smaller mesh ratio leads to more accurate results, but excessive emphasis on smaller meshes can cause more error and increase calculation time. The optimal shape of meshes is dependent on the geometry of object, so the best shape should be selected according to the geometry. Trial and error are used to obtain the most suitable mesh size. To do this, an initial mesh size is selected and the result is calculated based on this selection. In the next step, a smaller mesh will be selected and the results will be recalculated. This process will be continued until the results will converge to a certain amount. In this case, the final mesh will be considered as a suitable one. The appearance of the meshes can be square, triangle or other shapes, while square and triangle meshes are the most common ones. In this research, due to the square-shaped geometry of the RVE, square meshing is more suitable and it is used. Here, after a few rounds of trial and errors, and comparing the results with each other, it is seen that for a mesh size of 0.3, the results are converged to acceptable amounts (Fig. 6).

Fig. 6
figure 6

The final mesh of 2D RVE

Full size image

RVE analysis along with different nanotube volume fraction

In this section, nanotubes are added to the RVE and the analysis is carried out for different amounts of nanotube volume fraction. The effect of varying the number of nanotubes on longitudinal and transverse modulus, Poisson’s ratio and fiber pull-out force is investigated and then compared with each other. If the total volume of RVE assumed as \(\forall_{t}\), and the total volume fraction of nanotubes considered as \(\forall_{c}\), the following equation can be written for the nanotubes’ volume percent:

$$\% CNT = \frac{{\forall_{c} }}{{\forall_{t} }} = \frac{{n\left[ {\pi \left( {r_{o}^{2} - r_{i}^{2} } \right) \times h} \right]}}{A \times l}$$
(6)

In this equation, r i , r 0 and h are the internal, external radii and length of nanotube, respectively, and n is the number of nanotubes. Also, we have already known that A and L are the cross-section area and length of RVE, respectively. In this study, the internal and external radii of CNT are assumed to be 0 and 0.025 μm, respectively, and its length considered 1 μm. By setting 1–5 % volume fraction for the CNT, it can be possible to obtain the required number of nanotubes for the modeling. For the volume fraction of 1, 2, 3, 4, and 5, the number of CNTs is calculated as 478, 954, 1432, 1910 and 2386, respectively. Here, in this study the beam element is used to model the nanotubes. The resulting shape of the model which also included the nanotubes is shown in Fig. 7.

Fig. 7
figure 7

A 2D RVE including matrix, fiber and CNTs

Full size image

RVE analysis along with different length of nanotubes

Now, we assume that the volume fraction of all the RVE components including matrix, fibers and nanotubes is constant and the length of nanotube is changing. In this stage, by considering a volume fraction of 1 % for the nanotubes, their length could be varied from 300 to 1000 nm.

RVE analysis along with different diameter of nanotubes

In this section, the volume fraction of all the RVE components including matrix, fibers and nanotubes is constant and only the diameter of the nanotubes can be changed. By considering the constant volume percent of 1 % for the nanotubes, their diameter varies from 20 to 100 nm, and then its effects on the elastic properties of the composite are investigated.

Numerical results and discussion

Results obtained for the RVE with various nanotubes volume fraction

By placing the nanotubes with a volume percent ranging from 0 to 5 % in the RVE, the E 1, E 2 values, Poisson’s ratio and fiber pull-out force could be obtained. Its results are drawn as some figures versus different amounts of CNTs volume fraction. These results are compared with the values obtained from micromechanical model.

According to Fig. 8, the amount of longitudinal Young’s modulus (E 1) is almost unaltered based on the results provided using FEM, but it is observed that the results calculated through micromechanical method are linearly increasing and the increase in CNTs volume percent has a significant effect on longitudinal Young’s modulus. So, it can be said that micromechanical method cannot offer a kind of accurate results for the addition of nanotubes on the surface of fibers.

Fig. 8
figure 8

Variation of longitudinal Young’s modulus versus volume percent of nanotubes

Full size image

In the following, the effect of nanotubes on the transverse Young’s modulus of RVE is investigated (Fig. 9). According to the FEM results, it can be said that addition of 1–2 % of CNT can increase E 2 by about 13 %, and adding more than 2 % of CNT has no effects on the amount of E 2 and it remains almost unaltered with the increase of CNTs volume fraction; But the results which are obtained based on the micromechanical model show that the amount of transverse Young’s Modulus is increasing with the increase of volume percent of nanotubes. It is obvious that in the range of 0–5 volume percent of nanotubes the micromechanical results are about 5–15 % less than the results of FEM.

Fig. 9
figure 9

Variation of transverse Young’s modulus versus volume percent of nanotubes

Full size image

The variations of Poisson’s ratio versus volume percent of nanotubes are obtained through FE and Micromechanical method; these results are compared with each other as shown in Fig. 10. Both methods show that with the increase of volume percent of nanotubes the Poisson’s ratio is decreasing until it gets almost unaltered, but the rate of decrease in the Poisson’s ratio which is provided by FE method is greater than the Micromechanical method. The greatest difference between the two methods is about 7 %.

Fig. 10
figure 10

Variation of Poisson’s ratio versus volume percent of nanotubes

Full size image

According to Fig. 11, with the addition of nanotubes, the fiber pull-out force will be increased by about 1 % which indicates that with the addition of nanotubes, the connection between the fibers and the matrix will become stronger and it can result in the RVE strength.

Fig. 11
figure 11

Variation of pull-out force versus volume fraction of nanotubes

Full size image

Results obtained for the RVE with various nanotube lengths

FEM has been able to express the effects of length changes on the composite properties. By considering a constant volume fraction (1 %) for the nanotubes, their length is changed in the range between 0.3 and 1 µm and the elastic properties of the RVE are obtained. Given that the rule of mixture has not considered the effect of object dimensions, in all the following figures, it is observed that this method has not been able to express the effective properties of RVE properly; the amount of these properties remains unaltered which expresses the weakness of the rule of mixture theory at this kind of analysis.

Figure 12 shows the effect of changing the length of nanotubes on the longitudinal Young’s modulus. According to this figure, rule of mixture and FE methods reveal that longitudinal Young’s modulus remains unaltered with the increase of CNT length.

Fig. 12
figure 12

The effect of changing the length of nanotubes on the longitudinal Young’s modulus

Full size image

The effect of various amount of CNT length on the transverse Young’s MODulus is depicted in Fig. 13. FE method shows that with changing the CNT length in range of 0.3–1 µm, the amount of E 2 has been increasing by about 5 %.

Fig. 13
figure 13

The effect of changing the length of nanotubes on the transverse Young’s modulus

Full size image

The effect of various amount of CNT length on the Poisson’s ratio is given in Fig. 14. The micromechanical approach shows that there is no kind of changes on the amount of Poisson’s ratio as the CNT length is changing in range of 0.1–1 µm, but FE method provides some results showing that with the increase of CNT length in the same range, Poisson’s ratio sharply decreases.

Fig. 14
figure 14

The effect of changing the length of nanotubes on the Poisson’s ratio

Full size image

The variation of pull-out force versus the CNTs length is given in Fig. 15, as it is observed from this figure that the amount of pull-out force is sharply increasing up to 0.6 µm CNT length, then with the increase of CNT length the pull-out force decreases and it becomes almost unaltered for CNT length >0.9 µm.

Fig. 15
figure 15

The effect of changing the CNTs length on the amount of pull-out force

Full size image

Results obtained for the RVE with various nanotube Diameters

Like the previous section, the volume fraction of the nanotubes is assumed to be 1 %. Once again, it is seen that the micromechanical method cannot show the effect of changing CNTs diameter on longitudinal, transverse Young’s Modulus and Poisson’s ratio of nanotubes properly. Based on the results provided by micromechanical method, the amount of composite properties including transverse, longitudinal Young’s modulus and Poisson ratio will be constant, but the FEM properly shows the effect of changing CNTs diameter on composite properties. In the following, some figures are reported assuming that the CNTs diameter is changing in range of 0.02–1 µm.

According to Fig. 16, both approaches including FE and Micromechanical method show that with the increase of CNT diameter the amount of longitudinal Young’s modulus (E 1) remains constant.

Fig. 16
figure 16

The effect of changing the CNTs diameter on the longitudinal Young’s modulus

Full size image

It is observed from Fig. 17 that with the increase of CNT diameter the amount of E 2 is decreasing based of FE method, but the micromechanical approach provides some results showing that increasing the CNT diameter has not any effect on transverse Young’s modulus.

Fig. 17
figure 17

The effect of changing the CNTs diameter on the transverse Young’s modulus

Full size image

The effect of CNT diameter on the Poisson’s ratio is depicted in Fig. 18. As one can see, based on the results provided by FE method the Poisson’s ratio is increasing with the increase of CNT diameter. The Micromechanical method shows that the amount of Poisson’s ratio remains unaltered as the diameter of CNT is increasing.

Fig. 18
figure 18

The effect of changing the diameter of nanotubes on the Poisson’s ratio

Full size image

Figure 19 shows the variation of pull-out force versus CNT diameter. According to this figure, changing the amount of CNT diameter has a kind of significant effect on the pull-out force. It is observed that with the increase of CNT diameter the pull-out force sharply decreases.

Fig. 19
figure 19

The effect of changing the diameter of nanotubes on the pull-out force

Full size image

Conclusion remarks

This research work deals with FE and micromechanical modeling of nanocomposite polymer–matrix reinforced by microfibers; the microfibers are also strengthened by CNT arrays. The mechanical properties of the desired composite such as Young’s modulus and Poisson’s ratio are obtained through micromechanical model and theoretical formulas and, then, with the use of FE method, these properties are recalculated to compare with the results which are provided by micromechanical model. The results show that “generalized mixture rule (GMR)” cannot properly predict the effects of changing the length and diameter of nanotubes on the properties of the nanocomposites. Overall, it can be said that the addition of CNTs on the fiber surface has a positive effect on the elastic properties and strength of RVE. It is also shown that the RVE properties can be improved by increasing the volume fraction, length and decreasing diameter of nanotubes. From this study, some conclusions can be made:

  • According to micromechanical method, the values of the E 1 and E 2 of nanocomposite have been increased by 35 and 7 %, respectively, with the increase of CNTs volume fraction by about 5 %.

  • It is observed that based on the micromechanical method, the amount of E 1 and E 2 remains constant as the CNT length and diameter are increasing.

  • According to the results which are provided by micromechanical method, Poisson’s ratio decreases with the increase of CNTs volume fraction, but it is unaltered as the length and diameter of CNTs are increasing.

  • FEM results indicate that the value of E 1 does not change with the increase of CNTs length or diameter.

  • The FE results show that with the increase of CNT volume fraction (from 0 to 5 %) and length (from 0.3 to 1 µm), the value of E 2 increases by about 13 and 5 %, respectively, but with the increase of CNT diameter (from 0.02 to 0.1 µm), the amount of E 2 decreases by about 6 %.

  • It is observed that the Poisson’s ratio decreases by about 8 and 3 % with the increase of CNT volume fraction and length, respectively, But with the increase of CNT diameter, the Poisson’s ratio is increasing by about 4 %.

  • The fiber pull-out force has been increased by about 1 % with the increase of CNT volume fraction (from 0 to 5 %).

  • It is observed that the amount of pull-out force sharply increasing up to 0.6 µm CNT length, then with the increase of CNT length, the pull-out force decreasing and it becomes unaltered for long CNT (>0.9 µm).

  • Results indicate that changing the amount of CNT diameter has a kind of significant effect on the pull-out force; it is observed that with the increase of CNT diameter the pull-out force sharply decreases.