Introduction

Transportation infrastructure is one of the significant factor which reflects the development of a nation’s economy. Due to the paucity of land and increased traffic in urban areas, the bridges have become inevitable part of the transportation facilities, such as highways and railways. In recent years, with the rapid advances in the area of high-performance materials, design technologies and construction techniques, the architecture of bridges has reached unexpected limits. At the same course of time, day by day, the bridges are becoming more slender and lighter and hence more prone to vibrations due to heavy vehicles and high-speed trains passing over it. Thus, the vibration of a bridge due to the passage of vehicles is an important aspect in bridge design. A multi-axle vehicle moving over the bridge can be modeled as planar moving forces, inducing periodic excitations to the bridge. Vibrations induced by moving vehicles become excessive when the vehicle velocities reach resonant or critical values. This may seriously affect the long-term safety, serviceability of the bridges and comfort of the passengers. In addition, it may endanger the safety of supporting structure. Hence, it is very necessary to control these undesirable excessive vibrations of bridge under train loads.

Literature review shows that the dynamic behavior of the bridges has been significantly impacted due to periodic moving loads from trains; the same has been investigated by many researchers in the past few years.

Kwon et al. (1998) investigated the control efficiency of single-tuned mass damper (STMD) system attached with the bridges. He idealized the bridge as a simply supported Euler–Bernoulli beam traversed by vehicles which were modeled as moving masses and shown that TMD can effectively reduce response of the bridge. Yang et al. (1997) investigated the vibration of simple beam excited under high-speed moving trains and proposed a span to car length ratio so that no resonance occurs in beam. Chen and Lin (2000) investigated the dynamic response of elevated high-speed railway. Cheng et al. (2001) proposed a bridge-track-vehicle element for investigating interactions between moving train, railway track and bridge. Ju and Lin (2003) investigated the resonant characteristics of three-dimensional (3D) multi-span bridges subjected to high-speed trains. Wang et al. (2003) carried out the optimization of STMD attached at the mid-span of Taiwan high-speed railway (THSR) bridges subjected to French train à grande vitesse (TGV), German intercity express (ICE) and Japanese SKS trains. Nasiff and Liu (2004) presented a 3D dynamic model for the bridge-road-vehicle interaction system. Jianzhong et al. (2005) has performed a parametric study on the optimization of multiple tuned mass dampers (MTMD) and demonstrated its efficiency in reducing displacement and acceleration responses of simply supported bridge subjected to high-speed trains. Lin et al. (2005) proved that MTMD is more effective and reliable than STMD in reducing train-induced dynamic responses of simply supported bridges during resonant speeds. Shi and Cai (2008) performed numerical analysis to study the vehicle-induced bridge vibration response using a TMD, considering the road surface conditions. Li et al. (2010) developed a numerical method to analyze coupled railway vehicle-bridge systems of non-linear features. Moghaddas et al. (2012) studied the dynamic behavior of bridge-vehicle system attached with TMD, using the finite-element method. It was shown that by attaching an optimized TMD to a bridge, a significantly faster response reduction can be achieved. Antolin et al. (2013) considered non-linear wheel-rail contact forces model to analyze the dynamic interaction between high-speed trains and the bridges. Wang et al. (2013) investigated the effectiveness of visco-elastic damper (VED) to mitigate the multiple resonant responses of a moving train running on two-span continuous bridges. It is found that with the installation of VED at midpoint of each span, the maximum acceleration response of the bridge can be suppressed noticeably at resonant speeds.

It is evident from above studies that dynamic forces in the form of periodic moving loads from train may result in undesirable resonant responses of the bridge. These undesirable responses can be controlled using the TMD, MTMD and VED. However, TMD and MTMD are having disadvantages of being sensitive to the fluctuation in frequency spacing and tuning frequency with respect to the controlling (fundamental) frequency of the bridge. This may deteriorate the performance of TMD and MTMD. Until the date, the resonant response control of bridge is studied using TMD, MTMD and VED, but the use of friction dampers (FD) and tuned mass friction damper (TMFD) has not been explored for controlling the response of the bridges. Pisal and Jangid (2015) demonstrated that MTMFD can effectively reduce the seismic response of multi-storey structures.

In the present study, the performance of tuned mass friction damper (TMFD) in controlling undesirable resonant response of the bridge is investigated. To suppress the undesirable excessive responses of the bridge, different TMFD systems are employed. The specific objectives of the study are summarized as:

  1. 1.

    To formulate the equation of motion for the response of the bridge with different TMFD systems under periodic train loads and develop its solution procedure.

  2. 2.

    To investigate the influence of important parameters, such as mass ratio, tuning frequency ratio, frequency spacing, damper slip force and number of TMFD units in MTMFD on the performance of the MTMFD.

  3. 3.

    To obtain the optimum values of influencing parameters for TMFD and MTMFD systems, which may find application in the effective design of MTMFD for the bridges.

  4. 4.

    To investigate the performance of different TMFD systems, i.e., TMFD attached at the mid-span of the THSR bridge, MTMFD attached at the mid-span (concentrated) of the THSR bridge, and MTMFD distributed along the length of the THSR bridge subjected to Japanese SKS trains.

Modeling of vehicle, bridge and MTMFD

A train or any other vehicle which has multi-axle system excites a bridge when it passes over it. In contrast to wind or earthquake load, the position of vehicular load over the bridge changes at each and every second. Furthermore, due to the interaction between the vehicle and the bridge, the magnitude of vehicular load depends on the response of the bridge. Thus, it is difficult to establish the correlation between governing parameters and response of the bridge. Furthermore, time variant properties of the configured vehicle loading, bridge and TMFD system can make the modeling complex. To get an efficient and effective control performance of the TMFD system, it is necessary to select governing parameters appropriately. In the current study, simplified modeling of the vehicle and the bridge is considered to determine governing parameters. Once governing parameters are identified, model needs to be refined for doing further research. Finally, based on the simplified model of the vehicle, bridge and TMFD, coupled differential equations of motion is derived, the same has been solved numerically using the Newmark’s linear acceleration method.

The bridge is idealized as a simply supported Euler–Bernoulli beam with uniform properties throughout the length of the bridge. Track irregularity is neglected in the conceptualization of the model. The vibration of bridge is considered only in the vertical translational direction. The bridge is a continuous system which has infinite degrees-of-freedom (DOF), but only the first few modes of the bridge contribute significantly to the total dynamic response. Among all modes, the fundamental mode is dominating mode, especially for the displacement response of a simply supported bridge. Thus, for the present study, fundamental mode has been considered while finding out peak mid-span response of the bridge.

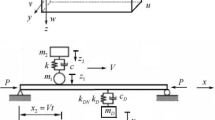
There are three basic modeling procedures of vehicles, namely, moving force, moving mass and moving suspension mass, as shown in Fig. 1 (Wang et al. 2003). In this study, the real-life multi-axle vehicle is modeled as a set of moving forces having equal axle spacing, moving along the centre line of the bridge. The axle spacing is an important parameter in the determination of critical resonating velocities of the vehicle which causes excessive vibrations in the bridge.

Fig. 1
figure 1

Schematic modeling of vehicles (Wang et al. 2003)

Full size image

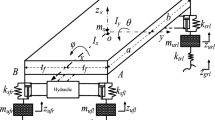
Arrangement considered for the present study consists of the bridge as primary system which is attached with TMFD and MTMFD with different dynamic characteristics. Here, the bridge is modeled as a simply supported Euler–Bernoulli beam.

Since, the maximum response of a simply supported bridge occurs at its mid-span, a TMFD system is installed at the mid-span of the bridge. In the case of MTMFD system, all the TMFD units can be concentrated at the mid-span or can be distributed along the length of the bridge. Figure 2 shows the simplified model of the bridge with MTMFD attached at equal intervals under the bridge and subjected to a train-induced excitation. The multi-axle train load is modeled as moving force with equal axle spacing. Assumptions/considerations are proposed for the present study in the following sub points:

Fig. 2
figure 2

Simplified model of bridge with MTMFD under multi-axle vehicle

Full size image
  1. 1.

    Stiffness of each TMFD unit is the same.

  2. 2.

    Normalized slip force value of each TMFD unit is the same.

  3. 3.

    The mass of each TMFD unit is varying. Thus, the natural frequency of each TMFD unit is adjusted to the required value by varying the mass.

  4. 4.

    The natural frequencies of the TMFD units in an MTMFD system are uniformly distributed around their average natural frequency. It is to be noted that the TMFD units of  a MTMFD system with identical dynamic characteristics are equivalent to a TMFD, in which the natural frequency of the individual TMFD units in  a MTMFD is the same as that of the equivalent TMFD.

  5. 5.

    For a simply supported bridge, dominating mode is the fundamental mode; hence, both TMFD as well as MTMFD systems are tuned to the fundamental natural frequency of the bridge.

Let \(\omega_{\text{T}}\) be the average frequency of all MTMFD and it can be expressed as:

$$\omega_{\text{T}} = \sum\limits_{j = 1}^{r}\frac{\omega_{dj}}{r},$$
(1)

where r is the total number of TMFD units in MTMFD, and \(\omega_{dj}\) is the natural frequency of the jth TMFD and it can be expressed as:

$$\omega_{dj}=\omega_{T}\left[{1 +\left({j -\frac{r + 1}{2}}\right)}\right]\frac{\beta }{r - 1},$$
(2)

where β is the dimensionless frequency spacing of the MTMFD, given as:

$$\beta =\frac{{\omega_{r}-\omega_{1}}}{{\omega_{\text{T}}}}.$$
(3)

If \(k_{dj}\) is the constant stiffness of each TMFD unit, then the mass of the jth TMFD unit is expressed as:

$$m_{dj}=\frac{{k_{dj}}}{{\omega_{dj}^{2}}}.$$
(4)

The mass ratio, which is defined as the ratio of total MTMFD mass to total mass of the bridge, is expressed as:

$$\mu =\frac{{\sum\limits_{j = 1}^{r}{m_{dj}}}}{mL},$$
(5)

where m is the mass per-unit length of the bridge, and L is the total length of bridge.

The ratio of average frequency of the MTMFD to the fundamental frequency of bridge is defined as tuning frequency ratio and is expressed as

$$f =\frac{{\omega_{\text{T}}}}{{\omega_1}},$$
(6)

where \(\omega_{1}\) is the fundamental frequency of the bridge. It is to be noted that as the stiffness and the normalized damper forces of all the TMFD are constant and only mass ratio is varying, the friction force adds up. Thus, the non-dimensional frequency spacing β controls the distribution of the frequency of TMFD units.

Governing equations of motion and solution procedure

Arrangement considered for the present study consists of the bridge as primary system which is subjected to a train-induced excitation. The train load is modeled as multi-axle moving force having equal axle spacing, as shown in Fig. 2. It is assumed that the train is compiled by total n w numbers of axles with equal axle spacing of x v and the numbering of axles is done in an ascending order from right to left. The rightmost and the leftmost axles over the bridge are numbered as r w and l w , respectively; each axle is transmitting a concentrated axle load of intensity P. The MTMFD is arranged under the bridge at equal interval of x T , with the leftmost TMFD at a distance of x TLS from the left support and the rightmost TMFD at a distance of x TRS from the right support. Each TMFD is a single-degree-of-freedom (SDOF) system pertaining to vibration along the vertical translational direction. The governing differential equation of the vertical motion of the bridge is:

$$\frac{{\partial^{2}}}{{\partial x^{2}}}\left[{E_{\text{m}}I_{\text{m}}(x)\frac{{\partial^{2}z_{\text{b}}\left({x,t}\right)}}{{\partial x^{2}}}}\right] + m(x)\frac{{\partial^{2}z_{b}\left({x,t}\right)}}{{\partial t^{2}}}+ c(x)\frac{{\partial z_{\text{b}}\left({x,t}\right)}}{\partial t}= P_{\text{V}}\left({x,t}\right) + P_{\text{T}}\left({x,t}\right),$$
(7)

where E m is the modulus of elasticity of the bridge material; I m(x) is the moment of inertia of uniform cross section of the bridge; c is the damping co-efficient of the bridge in the vertical direction; P V (x, t) is interacting force between the vehicle and the bridge; P T (x, t) is interacting force between the TMFD and the bridge and Z b (x, t) is vertical displacement of the bridge at a distance x and at time t.

$$\it P_{V}\left({x,t}\right) =\sum\limits_{{i = r_{w}}}^{{l_{w}}}{P\delta\big({x -\left({vt -\left({i - 1}\right)x_{V}}\right)}\big)},$$
(8)
$$ {\begin{aligned} P_{\text{T}}(x,t) &= \sum\limits_{j = 1}^{r}{\left[\begin{aligned}K_{dj}\left({Z_{dj}- Z_{\text{b}}\left({\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right),t}\right)}\right) + f_{sj}\;\text{sgn}\left({\dot{Z}_{dj}-\frac{{\delta Z_{\text{b}}\left({Z_{dj}- Z_{\text{b}}\left({\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right),t}\right)}\right)}}{\partial\,t}}\right)\hfill\\\end{aligned}\right]}\\ &\quad \;\times\delta\,\left({x -\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)}\right),\end{aligned}}$$
(9)

where P is the vehicular load, δ() is the Dirac delta function, v is the velocity of the vehicle, x v is the axle spacing of vehicle, sgn denotes the signum function, \(Z_{dj}\) is the vertical displacement of the jth TMFD and \(\dot{Z}_{dj}\) is the velocity of the jth TMFD.

The equation of motion of the jth TMFD can be expressed as:

$$m_{dj}{\textit{\"{Z}}}_{dj}+ K_{dj}\;\left({Z_{dj}- Z_{\text{b}}\left({\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right),t}\right)}\right) = - f_{sj}\;\text{sgn}\left({\dot{Z}_{dj}-\dot{Z}_{\text{b}}\left({\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right),t}\right)}\right),$$
(10)

where \(\dot{Z}_{\text{b}}\) is the vertical velocity of the bridge, and \(\textit{\"{Z}}_{dj}\) is the vertical acceleration of the jth TMFD.

Modal analysis has been carried out to separate governing parameters and solve Eqs. (7) and (10) analytically. The vertical displacement of the bridge can be expressed as the product of mode shape function, φ n (x) and modal response function, q n (t) involving only the spatial and temporal co-ordinates

$$Z_{\text{b}}(x,t) =\sum\limits_{i= 1}^{n}{\varphi_{n}}(x)q_{n}(t),$$
(11)

where n is the number of modes to be considered for bridge. Substituting Eq. (11) in Eq. (7) results in Eq. (12)

$$m\sum\limits_{i = 1}^{n}{\varphi_{n}}(x){\kern 1pt}\textit{\"{q}}_{n}(t) + c\sum\limits_{i = 1}^{n}{\varphi_{n}}(x){\kern 1pt}\dot{q}_{n}(t) +\sum\limits_{i = 1}^{n}{\left[{E_{\text{m}}I_{\text{m}}{\kern 1pt}\varphi^{\prime\prime}_{n}(x)}\right]^{\prime\prime}}q_{n}(t) = P_{\text{V}}(t) + P_{\text{T}}(t).$$
(12)

Multiplying each term of Eq. (12) by the mode shape function and integrating over the length of the bridge, we can obtain the following equation, after applying orthogonality principle of mode shape function for the nth mode of vibration of the bridge

$$M_{n}\textit{\"{q}}_{n}(t) + C_{n}{\kern 1pt}\dot{q}_{n}(t) + K_{n}q_{n}(t) = P_{nV}(x,t) + P_{nT}(x,t),$$
(13)

where M n , K n and C n are representing the modal mass, modal stiffness and modal damping of the nth mode, respectively; \(q_{n}(t)\), \(\dot{q}_{n}(t)\) and \(\textit{\"{q}}_{n}(t)\) represent the modal displacement, modal velocity and modal acceleration of the bridge in the nth mode of vibration, respectively. The modal interacting forces for the nth mode become:

$$P_{nV}(x,t) =\int\limits_{0}^{L}{\sum\limits_{{i = r_{w}}}^{{l_{w}}}{P\varphi_{n}(x)\;\delta\,\left({x -\left({v\,t - (i - 1)\,x_{\text{V}}}\right)}\right)}}=\sum\limits_{{i =\;r_{w}}}^{{l_{w}}}{P\varphi {}_{n}\left({v\,t - (i - 1)\,x_{\text{V}}}\right)},$$
(14)
$$P_{nT}(x,t) =\sum\limits_{j = 1}^{r}{\left[\begin{aligned}K_{dj}\left({Z_{dj}-\sum\limits_{i = 1}^{n}{\varphi_{i}}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,q_{i}(t)}\right) + f_{sj}{\kern 1pt}\text{sgn}\left({\dot{Z}_{dj}-\sum\limits_{i = 1}^{n}{\varphi_{i}}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,\dot{q}_{i}(t)}\right)\hfill\\\end{aligned}\right]}{\kern 1pt}\varphi_{n}\;\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right).$$
(15)

The natural frequencies and the mode shape functions for the nth mode of a simply supported bridge are given as:

$$\omega_{n}=\frac{n^{2}\pi^{2}}{L^{2}}\;\sqrt{\frac{E_{\text{m}}I_{\text{m}}}{m}},$$
(16)
$$\varphi_{n}(x) = \sin\left({\frac{n\pi\;x}{L}}\right).$$
(17)

The modal mass is the same for all the modes and is equal to half total mass of the bridge. Modify Eq. (13) by substituting M n  = mL/2 and replacing suffix n by 1 to obtain the equation of motion for the fundamental mode of vibration.

$$\frac{mL}{2}\textit{\"{q}}_{1}+ 2\left({\frac{mL}{2}}\right){\kern 1pt}\xi_{1}\omega_{1}\dot{q}_{1}+\frac{mL}{2}\omega_{1}^{2}q_{1}=\sum\limits_{{i = r_{w}}}^{{l_{w}}}{P\varphi {}_{1}}(v\,t - (i - 1)\,x_{\text{V}}) +\sum\limits_{j = 1}^{r}{\left[\begin{aligned}K_{dj}\left({Z_{dj}-\varphi_{1}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,q_{1}^{{}}}\right) + f_{sj}{\kern 1pt}\text{sgn}\left({\dot{Z}_{dj}-\varphi_{1}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,\dot{q}_{1}(t)}\right)\hfill\\\end{aligned}\right]}{\kern 1pt}\varphi_{1}\;\qquad\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right).$$
(18)

Similarly, the equation of motion for TMFD can be written as Eq. (19) by modifying Eq. (10)

$$m_{dj}\textit{\"{Z}}_{dj}+ K_{dj}\left({Z_{dj}-\varphi_{1}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,q_{1}}\right) = - f_{sj}\;\text{sgn}\left({\dot{Z}_{dj}-\varphi_{1}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,\dot{q}_{1}}\right).$$
(19)

Equation (20) represents the coupled equation of motion in matrix form for the bridge equipped with TMFD. This equation is obtained by combining Eqs. (18) and (19)

$$\left[{M_{1}}\right]\left\{ {\textit{\"{y}}_{1}}\right\}+\left[{C_{1}}\right]\left\{ {\dot{y}_{1}}\right\}+\left[{K_{1}}\right]\left\{ {y_{1}}\right\}=\left[ E\right]\left\{ {P_{1V}}\right\}+\left[ B\right]\left\{ {F_{s}}\right\},$$
(20)
$$\left\{ {y_{1}}\right\}=\left\{ {\begin{array}{*{20}c}{q_{1}}\\ {Z_{d1}}\\ {Z_{d2}}\\\vdots\\ {Z_{dr}}\\\end{array}}\right\},$$
(21)

where q 1 is the first modal displacement vector of the bridge, and \(Z_{dj}\) (j = 1 to r) is the displacement vector of TMFD units of MTMFD; [M 1], [C 1] and [K 1] denote the mass, damping and stiffness matrix of the configured system of order (r + 1) × (r + 1), respectively, considered for the study for the fundamental mode of vibration of bridge; [E] and [B] are placement matrices for the train-induced excitation force and friction force, respectively; y, \(\dot{y}\) and \(\textit{\"{y}}\) are the vertical displacement, velocity and acceleration vector of configured system, respectively; P 1V is the interacting force vector between the vehicle and the bridge in fundamental mode and F s denotes the vector of friction force provided by the TMFD. These matrices can be shown as:

$$\left[{M_{1}}\right] = {\text{diag}}\;\left[{\frac{mL}{2}\; m_{1}\;m_{2}\cdots m_{r}}\right],$$
(22)
$$\left[{C_{1}}\right] =\left[{\begin{array}{*{20}c}{mL\xi_{1}\omega_{1}}& 0 & 0 &\cdots & 0\\ 0 & 0 & 0 &\cdots & 0\\ 0 & 0 & 0 &\cdots & 0\\\vdots &\vdots &\vdots &\ddots &\vdots\\ 0 & 0 & 0 &\cdots & 0\\\end{array}}\right],$$
(23)
$$\left[{K_{1}}\right] =\left[{\begin{array}{*{20}c}\frac{mL}{2}\omega_{1}^{2}+\sum\limits_{j = 1}^{n}{K_{dj}\varphi_{1}^{2}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)}& { - K_{d1}\varphi_{1}(x_{\text{TLS}})}& { - K_{d2}\varphi_{1}(x_{\text{TLS}}+ x_{\text{T}})}&\cdots & - K_{dr}\varphi_{1}(x_{\text{TLS}}+ (r - 1)x_{\text{T}})\\ { - K_{d1}\varphi_{1}(x_{\text{TLS}})}& {K_{d1}\varphi_{1}(x_{\text{TLS}})}& 0 &\cdots & 0\\ - K_{d2}\varphi_{1}(x_{\text{TLS}}+ x_{\text{T}}) & 0 & {K_{d2}\varphi_{1}(x_{\text{TLS}}+ x_{\text{T}})}&\cdots & 0\\\vdots &\vdots &\vdots &\cdots & 0\\ - K_{dr}\varphi_{1}(x_{\text{TLS}}+ (r - 1)x_{\text{T}}) & 0 & 0 & 0 & K_{dr}\varphi_{1}(x_{\text{TLS}}+ (r - 1)x_{\text{T}})\\\end{array}}\right],$$
(24)
$$F_{s}=\left[{\sum\limits_{j = 1}^{r}{F_{sj}}\quad - F_{s1}\quad - F_{s2}\quad\cdots\quad - F_{sr}}\right],$$
(25)

where the friction force of the jth damper is given as:

$$F_{sj}= f_{sj}\,\text{sgn}{\kern 1pt}\left({\dot{Z}_{dj}-\varphi_{1}\left({x_{\text{TLS}}+\left({j - 1}\right)x_{\text{T}}}\right)\,\dot{q}_{1}}\right),$$
(26)

where \(\dot{Z}_{dj}\) shows the velocity of the jth TMFD, and \(\dot{q}_{1}\) shows the first modal velocity of the bridge. Furthermore, the damper forces are calculated using the hysteretic model proposed by Constantinou et al. (1990), using the Wen’s equation (Wen 1976), which is expressed as:

$$F_{sj} = f_{sj}\,Z,$$
(27)

where f sj is the limiting friction force or slip force of the jth TMFD, and Z is the non-dimensional hysteretic component, which satisfies the following first-order non-linear differential equation:

$$q\;\frac{{{\text{d}}Z}}{{{\text{d}}t}}= A\;(\dot{Z}_{dj}-\dot{q}_{1}) -\beta\;\left| {\left({\dot{Z}_{dj}-\dot{q}_{1}}\right)}\right|\,Z\;\left| Z\right|^{n - 1}-\tau\;\left({\dot{Z}_{dj}-\dot{q}_{1}}\right)\;\left| Z\right|^{n},$$
(28)

where q represents the yield displacement of frictional force loop, and A, β, τ and n are non-dimensional parameters of the hysteretic loop which controls the shape of the loop. These parameters are selected in such a way that it provides typical Coulomb-friction damping. The recommended values of these parameters are taken as q = 0.0001 m, A = 1, β = 0.5, τ = 0.05, and n = 2 (Bhaskararao and Jangid 2006). The hysteretic displacement component, Z, is bounded by peak values of ±1 to account for the conditions of sliding and non-sliding phases. The limiting friction force or slip force of the jth friction damper is expressed in the normalized form by \(R_{fj}\), which can be expressed as:

$$R_{fj} = \frac{{f_{sj}}}{{m_{dj}\times g}},$$
(29)

where g represents acceleration due to gravity.

The coupled differential equations are solved using the Newmark’s linear acceleration method (Chopra 2003).

Critical velocities of train

Dynamic response of the bridge becomes excessive under resonating conditions, i.e., when the vehicle velocities are critical. The critical velocities of the vehicle depends on the fundamental frequency of the bridge and axle spacing of the vehicle which can be expressed as (Wang et al. 2003):

$$v_{c}=\frac{{\omega_{1}x_{{v}}}}{2l\;\pi},$$
(30)

where \(\omega_{1}\) is the fundamental frequency of the bridge, x v is the vehicle’s axle spacing and \(l = 1, 2, 3,\ldots\) etc. At these critical velocities of the vehicle, the dynamic response of the bridge becomes excessive, generally when l = 1. Thus, the resonant responses occurring due to the first critical velocity v c for i = 1 are of major concern.

Numerical study

The THSR bridge that is considered for the numerical study and properties of this bridge is listed in Table 1 (Wang et al. 2003). The bridge is subjected to Japanese SKS train, modeled as a series of moving planar forces with the same magnitude of axle load and equal axle spacing. The properties of this Japanese SKS train have been presented in Table 2. The bridge undergoes resonant vibration whenever the velocity of the train reaches its critical value. The response quantity of interest for the study is the mid-span vertical displacement of the bridge.

Table 1 Properties of the THSR bridge
Full size table
Table 2 Properties of model of Japanese SKS train
Full size table

For numerical study, TMFD and MTMFD systems are installed under the bridge. Maximum displacement response of the simply supported bridge occurs at mid-span; hence for the proposed TMFD system, the damper is placed at the mid-span of the bridge. In the case of MTMFD systems, all the TMFD units can be concentrated at the mid-span or can be distributed at an equal interval along the length of the bridge. Furthermore, for distributed MTMFD system, the TMFD units are distributed at an interval of 2 and 5 m, respectively. Time interval, Δt = 0.001 has been considered for numerical solution. The performance of the bridge installed with TMFD system has been compared with the uncontrolled response of the bridge.

Uncontrolled response of the bridge under train load

The generalized responses of the first three modes of the THSR bridge without the installation of TMFD under the effect of Japanese SKS train induced vibration is studied. It is seen that both dynamic displacement as well as dynamic acceleration responses are dominated by fundamental mode and the contribution of higher modes can be neglected to approach at the feasible solution for response. The contribution of the first three modes towards vertical displacement of THSR bridge subjected to Japanese SKS train is 5.249, 0.205 and 0.026 mm, respectively, and that towards acceleration response is 3.028, 1.301 and 0.122 m/s2, respectively. Therefore, it is apparent that only fundamental mode requires to be considered especially for the displacement response in practice. As excessive dynamic displacement affects the long-term safety, serviceability of the bridge and comfort of the passenger, hence, main focus of study is on the dynamic displacement and fundamental mode of vibration of the bridge.

To study the response of the bridge with respect to varying the velocity of the vehicle, the peak mid-span vertical displacement and acceleration response of the bridge are plotted in Fig. 3, against varying the velocity of the vehicle. It is observed that the displacement and acceleration responses of the bridge become excessive at the first critical train velocity, which confirms the agreement of Eq. (30), that for higher values of l, the critical velocities are lower and the corresponding response peaks are not large and do not require to be controlled practically. The time history of uncontrolled displacement and acceleration responses at mid-span of the bridge along the vertical translational DOF for the first critical velocity of Japanese SKS train moving over the bridge are shown in Fig. 4. It shows that the dynamic responses of the bridge become excessive when the vehicle moving over it runs at critical velocities, leading to the resonating conditions. The critical velocity depends on the fundamental frequency of the bridge and the axle spacing of vehicles.

Fig. 3
figure 3

Peak mid-span responses of bridge against vehicle velocities

Full size image
Fig. 4
figure 4

Time history responses at the mid-span of bridge for the first resonant vehicle velocities

Full size image

Controlled response of bridge and optimization of parameters

To control response of the bridge, different TMFD systems are concentrated at the mid-span of the bridge or distributed at an equal interval along the length of the bridge. These systems perform effectively only when the appropriate value of controlling parameters, namely, frequency spacing, tuning frequency ratio, damper slip force R f and number of TMFD units in an MTMFD, is selected. In the case of inaccurate selection of these parameters, the system may under-perform and the responses may not reduce effectively up to a desirable value. Hence, the optimization of the parameters of TMFD systems is a very important criterion for its effective functioning. In this study, the parameters are optimized to reduce the peak mid-span displacement response of the bridge to its minimum value.

The mass ratio of all the TMFD units of MTMFD systems is kept the same as that of TMFD system. However, the criteria of optimization of parameters of all the TMFD systems (TMFD, concentrated MTMFD and distributed MTMFD) are the same, i.e., the minimization of peak mid-span displacement response of the bridge. After the selection of the number of TMFD units in MTMFD systems and the mass ratio of TMFD system, the maximum responses of the bridge subjected to multi-axle vehicles are studied.

Optimization of parameters for concentrated TMFD

The variation of the optimum parameters, β opt, f opt, and \(R_{\text{f}}^{\text{opt}}\) against the number of TMFD units in an MTMFD system concentrated at the mid-span of the bridge is shown in Fig. 5. It is observed that the optimum frequency spacing, β opt, increases sharply with the increase in the number of the TMFD units and beyond certain numbers of TMFD units, it increases gradually. Similarly, the optimum frequency ratio, f opt, increases with the increase in the number of TMFD units and remains constant after a certain number of TMFD units. The optimum value of normalized slip force, \(R_{\text{f}}^{\text{opt}}\), of MTMFD system is much lower than single TMFD system. It is visible from the plot that the optimum values of \(R_{\text{f}}^{\text{opt}}\) reduce sharply with the increase in the number of TMFD units, up to a certain number of TMFD units, and beyond this number, the response curve becomes flatter. It is also observed from the response plot that with the increasing number of TMFD units, the peak response reduces monotonically up to a certain number of TMFD units and after that the reduction becomes insignificant. In the present case, the increase in the number of TMFD units beyond 5 will make the reduction of dynamic displacement response of THSR bridge practically insignificant. Hence, in this present context, the MTMFD system is selected with five TMFD units. Thus, an optimum value of controlling parameters, such as, β opt, f opt, and \(R_{\text{f}}^{\text{opt}}\) varies with respect to the number of TMFD units at which system can perform effectively.

Fig. 5
figure 5

Variation of optimum parameters and peak mid-span response of bridge against the number of TMFD units concentrated at the mid-span of bridge

Full size image

The peak mid-span displacement response of the bridge is plotted against various controlling parameters of TMFD systems in Fig. 6 for the mass ratio of 2 % for TMFD and concentrated MTMFD system (containing five numbers of TMFD units). In Fig. 6a, the response of system is plotted against the varying values of frequency spacing, keeping the optimum value of tuning frequency ration and R f constant. Similarly, in Fig. 6b, the optimum value of frequency spacing and R f is kept constant for each TMFD system and the response of the system is plotted against tuning frequency ratio. In addition, Fig. 6c shows the response of system against varying the values of R f for both the TMFD systems, keeping the optimum value of tuning frequency ratio and frequency spacing constant. It is observed from Fig. 6 that the MTMFD system is sensitive to the frequency spacing. In addition, peak mid-span displacement response of the bridge reduces to its minimum value at a particular value of tuning frequency ratio, frequency spacing and R f for each TMFD unit. The optimum parameters of concentrated MTMFD system are summarized in Table 3. Thus, MTMFD system is sensitive to the frequency spacing. At the optimum value of controlling parameters, namely frequency spacing, tuning frequency ratio and R f and optimum number of TMFD units, the response of the bridge reduces to its minimum value.

Fig. 6
figure 6

Peak mid-span displacement responses of bridge against different TMFD parameters

Full size image
Table 3 Optimum parameters of TMFD systems
Full size table

Optimization of parameters for distributed MTMFD

To optimize the parameters of distributed MTMFD, the TMFD units of MTMFD are distributed at an equal interval of 2 and 5 m, respectively, along the length of the bridge. For a fixed number of TMFD units distributed at fixed interval, the parameters can be optimized in a similar way as optimized for concentrated MTMFD system with the same governing criteria of minimization of peak mid-span displacement response of the bridge. In this study, the distributed MTMFD system is always placed symmetrically with respect to the mid-span of the bridge with the heaviest TMFD unit always at the mid-span and the mass of TMFD unit decreasing with its distance from the mid-span on either side, hence, only odd number (minimum three) of TMFD units are considered to comprise the distributed MTMFD system. The maximum number of TMFD units which can be used depends on the length of the bridge and the interval of TMFD units. Figure 7 shows that the nature of variation of optimum parameters with respect to the number of TMFD units composing the distributed MTMFD system is very similar to that of concentrated MTMFD system shown in Fig. 5, if the TMFD units are distributed at a fixed interval of 2 m. The optimum frequency spacing and optimum tuning frequency ratio increase with the increasing number of TMFD units. The optimum normalized slip force, \(R_{\text{f}}^{\text{opt}}\), of MTMFD system is lower than TMFD system, as it reduces with the increase in the number of TMFD units up to a certain number of TMFD units and after that the response curve becomes flatter. Similar to the case of concentrated MTMFD system, the peak mid-span displacement response of the bridge reduces monotonically with the increase in the number of TMFD units of distributed TMFD system up to a certain number of TMFD units and beyond this number, and the rate of response reduction becomes practically insignificant.

Fig. 7
figure 7

Variation of optimum TMFD parameters and peak mid-span response of bridge against the number of TMFD units distributed at a fixed interval of 2 m along the length of the bridge

Full size image

Like concentrated MTMFD, the optimum parameters of distributed MTMFD system are summarized in Table 3. The responses shown in Fig. 7d are the minimized peak mid-span displacement responses of the bridge, considering optimum values of controlling parameters corresponding to each number of TMFD units. Thus, the optimum frequency spacing of MTMFD system increases with the number of TMFD units of MTMFD system. The optimum tuning frequency ratio increases with the number of TMFD units. The optimum R f reduces with the increase in the number of TMFD units. The optimum R f of TMFD is much higher than that of MTMFD system. The response of the bridge decreases with the increase in the number of TMFD units of a distributed MTMFD system up to a certain number of TMFD units and after that the reduction of response becomes practically insignificant which shows an optimum number of TMFD units in distributed MTMFD exists. For the present study, the optimum number of TMFD units is selected as 5 to compose distributed TMFD system.

Effect of distribution of TMFD units along length of bridge

The effect of distribution of TMFD units along the length of the bridge is studied in Fig. 8. For this purpose, five TMFD units are distributed with equal interval of different values along the length of the bridge. It is observed that with the increase in the interval of the TMFD units, the peak mid-span displacement and acceleration response of the bridge increase. Thus, the MTMFD system consisting of five TMFD units is most effective when all the TMFD units are concentrated at the mid-span of the bridge, i.e., when the interval is zero, and its efficiency in reduction of bridge responses decreases with the increase in interval of the TMFD units. Thus, the MTMFD is most effective, if all the TMFD units are concentrated at the mid-span. Wang et al. (2013) has shown that the maximum response of the bridge can be noticeably suppressed if VED is installed at the midpoint of each span of the bridge, and the same is also confirmed for MTMFD system having all the TMFD units concentrated at the mid-span of the bridge.

Fig. 8
figure 8

Peak mid-span displacement and acceleration response of bridge for varying interval of TMFD units of MTMFD system having five-TMFD units distributed along the length of the bridge at an equal interval

Full size image

Effect of mass ratio

The effect of mass ratio on the performance of different TMFD systems is studied in Fig. 9 by plotting the peak mid-span displacement and acceleration response of the bridge against the varying mass ratio for different TMFD systems, namely, TMFD, concentrated MTMFD and MTMFD distributed at 2 m interval. It is observed that the peak mid-span responses of the bridge decreases with an increase in the mass ratio of all the TMFD systems up to a certain value of mass ratio and after that it gradually increases. In addition, the reduction is maximum for concentrated MTMFD system and minimum for TMFD system. Thus, similar to the optimum controlling parameters, an optimum value of mass ratio exists for all the TMFD systems, at which the response reduction of the bridge is maximum. In addition, the distributed MTMFD system having optimized controlling parameters with appropriately distributed TMFD units within a certain interval can be more effective than a TMFD.

Fig. 9
figure 9

Peak mid-span displacement and acceleration response of bridge against mass ratios of different TMFD systems

Full size image

Resonant response control of the bridge with different TMFD systems

In this section, the effectiveness of TMFD, concentrated MTMFD and distributed MTMFD systems in the reduction of excessive dynamic responses of the bridge under the excitations induced by moving multi-axle vehicle is highlighted. The functioning of different TMFD systems is compared with the help of figures. The distribution of mass of TMFD and TMFD units of MTMFD system are mentioned in Table 4. It is observed from Figs. 10 and 11 that optimized TMFD systems are very effective in the reduction of resonant displacement as well as acceleration responses of bridge under excitations induced by moving multi-axle vehicles. All the TMFD systems are effective at, or very near to the vicinity of resonant zone only, and apart from this zone, they are not so effective. This is because the TMFD systems are sensitive to the frequency change, and in this study, the TMFD system are tuned to the resonating frequency of the bridge. Furthermore, the comparative study of performance of all the TMFD systems shows that at resonating condition, the maximum reduction of mid-span displacement and mid-span acceleration responses is achieved with the use of optimized concentrated MTMFD systems, i.e., placing all the TMFD units at the mid-span of the bridge. It is also observed that when the same number of TMFD units is distributed at a fixed interval of 2 and 5 m, respectively, along the length of the bridge, it becomes less effective than a concentrated MTMFD system, but if the frequencies of the TMFD units are optimized efficiently, and they are placed at an interval within a certain limit then this distributed system becomes more effective than a TMFD system in the reduction of resonant responses of the bridge. In this present case, it is observed that an optimized distributed MTMFD system consisting of five TMFD units is more effective than an optimized TMFD system when the interval of the TMFD units is 2 m, but at the same time, it is less effective when the interval becomes 5 m. Thus, all the optimized TMFD systems are very effective in reducing the resonant displacement as well as acceleration responses of the bridge at or very near to the vicinity of resonant zone and a very part from this zone, they are not so effective. An optimized concentrated MTMFD system is the most effective system in reducing the resonant displacement and acceleration response of the bridge. When the number of TMFD units of an MTMFD system is distributed at a fixed interval along the length of the bridge, it becomes less effective than a concentrated MTMFD system, but if the frequencies of TMFD units are optimized efficiently, it becomes more effective than a TMFD system in reducing the resonant responses of bridge.

Table 4 Mass distribution of TMFD units of different TMFD systems
Full size table
Fig. 10
figure 10

Peak mid-span displacement response of the bridge against the varying vehicle velocities with different TMFD systems

Full size image
Fig. 11
figure 11

Peak mid-span acceleration response of the bridge against the varying vehicle velocities with different TMFD systems

Full size image

Furthermore, the performance of all the optimized TMFD systems is studied at different sections along the length of the bridge and is represented in Figs. 12 and 13. It is observed that all the TMFD systems are effective in reducing displacement as well as acceleration responses of the bridge at all the considered sections along its length, with the reduction being maximum at the mid-span of the bridge. It is also observed that the optimized MTMFD system consisting of five TMFD units concentrated at the mid-span of the bridge significantly reduces the response of the bridge at all the considered sections, under the influence of moving multi-axle vehicle. The reduction with the optimized TMFD system is less than the reduction with optimized MTMFD (consisting of five TMFD units) system distributed at 2 and 5 m interval. Thus, all the optimized TMFD systems are effective in reducing the resonant displacement and acceleration responses at all the sections of the bridge, with the maximum reduction at the mid-span of the bridge.

Fig. 12
figure 12

Peak displacement responses at different sections of bridge along its length with different TMFD systems

Full size image
Fig. 13
figure 13

Peak acceleration responses at different sections of bridge along its length with different TMFD systems

Full size image

The mid-span displacement and acceleration responses of the bridge with installation of different TMFD systems are listed in Table 5. It shows that all the TMFD systems appreciably reduces the mid-span displacement and acceleration response of the bridge. MTMFD system which is concentrated at the mid-span of the bridge can reduce displacement response up to 60.28 % and acceleration response up to 77.87 %, respectively.

Table 5 Peak mid-span displacement and acceleration responses of bridge with different TMFD systems
Full size table

Conclusions

The performance of MTMFD in controlling the undesirable response of the bridge is investigated. Simplified model of THSR bridge and Japanese SKS train is prepared, and the velocities of train causing undesirable resonant responses in the bridges are considered. To suppress excessive resonant responses of the bridge, different TMFD systems are employed under the bridge. The optimum parameters of different TMFD systems are found out with the criteria of minimization of peak mid-span displacement response of the bridge. The effect of distribution of TMFD units along the length of the bridge for MTMFD system is also investigated. On the basis of trends of results obtained, the following conclusions are drawn:

  1. 1.

    The dynamic responses of the bridge become excessive when the vehicle moving over it runs at critical velocities, leading to the resonant conditions. The critical velocity depends on the fundamental frequency of the bridge and the axle spacing of the vehicles.

  2. 2.

    An optimum value of controlling parameters, such as, β opt, f opt, and \(R_{\text{f}}^{\text{opt}}\) varies with respect to the number of TMFD units at which system can perform effectively.

  3. 3.

    MTMFD system is sensitive to the frequency spacing. At the optimum value of controlling parameters, namely, frequency spacing, tuning frequency ratio and R f and optimum number of TMFD units, the response of the bridge reduces to its minimum value.

  4. 4.

    The MTMFD is most effective if all the TMFD units are concentrated at the mid-span.

  5. 5.

    An optimum value of mass ratio exists for all the TMFD systems, at which the response reduction of the bridge is maximum.

  6. 6.

    All the optimized TMFD systems are very effective in reducing the resonant displacement as well as acceleration responses of the bridge at or very near to the vicinity of resonant zone and very apart from this zone, they are not so effective. An optimized concentrated MTMFD system is the most effective system in reducing the resonant displacement and acceleration response of the bridge.

  7. 7.

    When the number of TMFD units of  a MTMFD system is distributed at a fixed interval along the length of the bridge, it becomes less effective than a concentrated MTMFD system, but if the frequencies of TMFD units are optimized efficiently, it becomes more effective than a TMFD system in reducing the resonant responses of the bridge.

  8. 8.

    All the optimized TMFD systems are effective in reducing the resonant displacement and acceleration responses at all the sections of the bridge, with the maximum reduction at the mid-span of the bridge.

  9. 9.

    This study can be continued in the future to investigate the effect of track irregularity, lateral displacement, 3D effect of bridge-vehicle system on the response of the bridge. In addition, the performance of continuous span of the bridge with some rigid supports can be studied, using different TMFD systems.