Simulation and experimental study of rheological properties of CeO₂–water nanofluid

Abstract

Metal oxide nanoparticles offer great merits over controlling rheological, thermal, chemical and physical properties of solutions. The effectiveness of a nanoparticle to modify the properties of a fluid depends on its diffusive properties with respect to the fluid. In this study, rheological properties of aqueous fluids (i.e. water) were enhanced with the addition of CeO₂ nanoparticles. This study was characterized by the outcomes of simulation and experimental results of nanofluids. The movement of nanoparticles in the fluidic media was simulated by a large-scale molecular thermal dynamic program (i.e. LAMMPS). The COMPASS force field was employed with smoothed particle hydrodynamic potential (SPH) and discrete particle dynamics potential (DPD). However, this study develops the understanding of how the rheological properties are affected due to the addition of nanoparticles in a fluid and the way DPD and SPH can be used for accurately estimating the rheological properties with Brownian effect. The rheological results of the simulation were confirmed by the convergence of the stress autocorrelation function, whereas experimental properties were measured using a rheometer. These rheological values of simulation were obtained and agreed within 5 % of the experimental values; they were identified and treated with a number of iterations and experimental tests. The results of the experiment and simulation show that 10 % CeO₂ nanoparticles dispersion in water has a viscosity of 2.0–3.3 mPas.

Introduction

The thermo-physical applications are creating an opportunity for a wide use of nanoparticles in fluids. The use of the CeO₂ nanofluids for enhancing the thermo-physical and rheological properties has shown to be important in applications such as plate heat exchanger, fuel cells, tribology [1], heat transfer [2], coolant material [2], metal polishing, UV absorbent [3] and filters. The dependencies on nanoparticles are increasing due to their characteristics of high surface area to volume ratio, size, and stability where different nanoclusters show diffusive and thermo-physical enhancements [4–6]; likewise, CeO₂ nanoclusters have capabilities of promoting different properties when dispersed in various fluids. It has been seen that CeO2 nanoparticle stability in water is low [1], whereas the stability can still be enhanced by modifying agents.

The improvement in dispersibility of CeO2 nanoparticles by surfactant Sorbitan monostearate in water demonstrated contribution to friction reduction [1, 7]. The application of this additive was able to reduce the friction coefficient of the water-based lubricant effectively, i.e. good for tribology applications. Later, wear scar depth observed with water-based CeO₂ nanofluid presented less enhanced antiwear properties than the CeO₂ modified with Sorbitan monostearate as investigated by Zhao et al. [7]. Later, ceria-based water nanofluids showed improvements in convective heat transfer applications; these nanofluids are capable of enhancing the heat transfer coefficient to about 39–40 % in a plate heat exchanger [2].

However, the CeO2 simulations were carried out to study the phase separation and particle aggregation, as Conesa investigated the CeO₂ surface structural stability analysis simulations using molecular mechanics. Their simulations through molecular mechanics were 10 % in contrast with experimental results for bulk modulus of CeO₂ [8].

Moreover, the metal oxides nanoparticles of silica (SiO₂), ceria (CeO₂), and alumina (Al₂ O₃) nanofluids at low concentrations with a particle size of 10 nm and 20 nm in pool boiling have been analysed. When these particles do not deposit on the wire, the nanofluid with metal oxides suspension increases critical heat flux by about 50 %, irrespective of the type of the oxide particle and its size [9].

Furthermore, Baudin et al. discussed the structural energies and surface properties over different orientations of the CeO₂ by molecular dynamics using NPT ensemble [10–12].

Apart from nanofluid’s simulations, all these simulations that are mostly related to the structural analysis of CeO₂ nanoparticles are beneficial and easily available. The CeO2 nanoparticles higher usages in different fluids make it important to simulate. Hence, due to the wide applications of CeO₂ nanofluid, this study presents an investigation of the dispersion of CeO₂ nanoparticles in water-based nanofluids using molecular dynamics simulation.

In our study, we have discussed about the rheological and diffusive properties of nanoparticle in aqueous medium since the nanoparticles hold greater effect on altering the rheological regime of the solution. Moreover, we have analytically solved the full interactive system integrals to evaluate the viscosity through the Green–Kubo formula and compared it with the results of the experimental approximation. Furthermore, the viscosity of the CeO₂ nanoparticles in water system has not yet been known, since there is less research with respect to the viscosity calculation of this nanoparticle. There are some research available regarding viscosity analysis of CuO nanoparticles [13, 14] and Al₂O₃ nanoparticles dispersed in water [15, 16]. Thereby, the necessity of this research can be understood from our previous statement for other metal oxide nanoparticles application and experimental studies, since in this research experimental results trends have been compared with the simulative achieved results.

However, this study has been adopted from the review of molecular dynamics approach for nanoparticle dispersion simulation as proposed by Loya et al. [17].

Methodology

CeO₂ nanoparticles of 10–40 nm diameters and 99.9 % purity (Shandong Yitong, China) were first dispersed in water by ultrasonication device for 3 min at 200 watts using Hielschers US200 ultrasonicator. Later, the nanofluids viscosity was measured using a rheometer, i.e. TA instrument 1500Ex. The measurement was taken from 293 to 323 K.

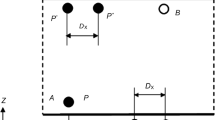
Moreover, simulations were performed on CeO₂ nanoparticles dispersed in TIP3P water using LAMMPS [18]. A CeO₂ nanoparticle was formed using Material studio from Accelrys Ltd UK. Later, both nanoparticle and water were introduced in one system. Charges on the atoms were assigned using COMPASS force field [19]. Moreover, two pair potentials, i.e. DPD and SPH [20] in hybrid style were used to execute the hydrodynamics and Brownian motion in the system. There were 40 CeO₂ nanoparticles of 1 nm in size, within 8000 TIP3P water molecular system as shown in Fig. 1. The first system consisted of around 10 % volume fractions of particles. The second system consisted of 4 CeO₂ nanoparticles of 1 nm that hold approximately 1 % of volume fractions. The system was equilibrated for three different temperature settings between 293 and 323 K.

Fig. 1

40 CeO2 (1 nm) nanoparticles in 8000TIP3P water molecular system;blue coloured atoms are of TIP3P water and nanoparticles are in white and red colour

Results

The viscosity of CeO₂ nanoparticle dispersion was analysed by a TA 1500Ex instrument. The experimental viscosity trends were gathered and compared with the obtained simulation results. As the nanoparticles were similar in their volumetric concentrations, remarkable trends were achieved and were compared. The data from the simulation were quantified for their accuracy by stress autocorrelation functions (SACF).

The time taken to simulate depends on the number of atoms in the system and the statistical analysis required to be performed. The correct selection of the time step is necessary for computation. Since this correlates with the decaying of the SACF, it is necessary for the SACF to decay monotonically to analyse the real statistical observation of average viscosity. Therefore, the results of the viscosity achieved through simulation are convincible till the SACF decay monotonically to zero as shown in Fig. 6, which was the case found with our simulation results as shown in Fig. 2.

Fig. 2

Measured viscosities of CeO₂ nanoparticles in water from temperatures 300–325 K

Furthermore, the analysis also used radial pair distribution functions. This function mathematically helps to determine the atomic pair distance between two consecutive atoms. This function is approached for agglomeration and dispersibility analysis.

Viscosity

As noted in Eq. 1, the simulation viscosity calculation carried out in this study was done using the Green–Kubo method. This method performs non-equilibrium molecular dynamics. The results of the viscosity measured by experiment and simulation are presented in Fig. 2.

Non-equilibrium methods have become increasingly popular for calculating the viscosity of liquids. The application of non-equilibrium methods is often simplified by the concept of pressure fluctuation-based equilibrium methods as shown in Eq. 1, such as those using the Green–Kubo method.

$$\mathit{\eta }=\frac{V}{3k_{\text{B}}T}\underset{0}{\overset{\infty }{\int }}〈\sum _{x<y}{P}_{xy}(t)P_{xy}(0)〉\text{d}t$$

(1)

The results of the viscosity of water with nanoparticles were in good agreement with the results obtained from simulations, but the correlation function took a lot of time to converge, which is shown in Fig. 6. The trends of the simulation viscosity result were concurrent to the experimental achieved values; however, they were within 5 % of discrepancies.

Later, the stress tensor is used to validate the accuracy of achieved viscosity reading by integrating the stress tensor with respect to time correlation as presented in “Stress autocorrelation function”.

Mean square displacement

Mean square displacement was used to calculate the diffusion coefficient of the system by taking the slope of the line achieved from the diffusion trajectories of the simulation [21]. The diffusion coefficient was also calculated to analyse the system aggregation and viscous regime. However, the diffusion in the CeO–water system is due to the layering of nanoparticles with water molecules and nanoparticle–nanoparticle layer forming a stabilized system. Hydrodynamic layering also affects the diffusion, especially in our case, as we are using water, the effect of hydrodynamic layering cannot be neglected. The TIP3P water self-diffusion coefficient is roughly 0.5–0.7E−9 m²/s as investigated [22]. This shows that the results achieved in this study are realistic [23, 24]. The diffusion coefficients were calculated by Eq. 2 and are presented in Fig. 3.

Fig. 3

Diffusion graphs of CeO₂ nanoparticles in water for temperatures 300–325 K

$$D=\frac{1}{6}d{\left(r_i(t)-r_i(0)\right)}^2/\text{d}t$$

(2)

Discussion

As already discussed in the results section, in the nanoparticle–water system, important factors that contribute towards the particle–particle interactions and changing the dispersibility of the system are diffusion coefficient and viscosity. Later, the viscosity achieved from the simulation can be further validated using the stress autocorrelation function; radial distribution function has been discussed to understand the aggregation nature of the CeO₂ nanoparticle system.

Radial distribution function

Radial distribution function, also known as the pair distribution function, is the essential link between macroscopic thermodynamic properties and intermolecular interactions of fluids and fluid mixtures. RDF theories were effective in describing the behaviour of simple liquids and liquid mixtures. Ce atoms in water system show less aggregation as seen from Fig. 4. At 0.3–0.4 nm a strong peak is observed due to the Ce–Ce interaction within the nanoparticle bond, whereas the peaks after 2 nm shows lower intensities; these peaks relate to the distance between Ce atom of one nanoparticle to another nanoparticle.

Fig. 4

Radial distribution function of Ce in water

Further, RDF is used for understanding the self-assembly (i.e. aggregation) of nanoparticles, that can be concerned as a fundamental question and this is also dependent on atom to atom shearing stress, i.e. the viscosity of the system. In this way, the interactions involved in controlling the self-assembly and aggregation mechanism can be understood. However, the experimental determination of these forces still remains a challenging task. On the other hand, theoretical methodologies such as radial distribution function in MD can be used to help understand the atomic interactions.

Density

Later, the density was analysed through MD simulation as shown in Fig. 5 and compared with the experimental and theoretical density. The theoretical density was calculated using Eq. 3. Whereas experimental density was found to be around 1.02 kg/m³, the theoretical density was calculated to be around 1.06 kg/m³. The difference between the theoretical and MD density is low. This shows (Fig. 6) that the system was properly configured.

Fig. 5

Density of CeO₂ nanoparticles in water from MD simulation

Fig. 6

Stress autocorrelation function graphs for validation of achieved viscosity of CeO₂ nanoparticles in water from MD simulation; a SACF for 303 K, b SACF for 313 K and c SACF for 323 K

$${\mathit{\rho }}_{\text{nf}}=\left(1-\mathit{\phi }\right){\mathit{\rho }}_{\text{f}}+\mathit{\phi }{\mathit{\rho }}_{\text{p}}$$

(3)

Stress autocorrelation function

Validation of the measured viscosity is carried out through stress tensors. The stress tensor equation Eq. 4 [25] has three components for controlling the stress in a particular direction. This formula can be used with molecular dynamics simulations. However, alternative formulations based on particle displacement require translational invariance, an assumption violated in MD simulations utilizing periodic boundary conditions. The summation within the angle brackets in Eq. 4 implies averaging of a ‘adequately large’ number of samples [26]. The specified term P _xy in Eq. 4 is the tensor for x–y direction, whereas there are other independent terms of the shear viscosity that are used as off-diagonal components of the stress. These terms are P _xz and P _yz . To implement Eq. 4, the optimal way is to use specific quantities. These quantities include the duration of the MD simulation, Δt, and the number of particles, N.

$$C_{xy}(t)=〈\sum _{x<y}{P}_{xy}(t)P_{xy}(0)〉$$

(4)

The monotonic decay of stress autocorrelation function for the CeO₂–water nanoparticle system presented different time steps for various temperatures, i.e. for 303 K, the system decayed in 0.125 fs, whereas for 313 K it decayed in 0.135 fs and for 323 K decayed in 0.15 fs. Further, the SACF showed that the decaying function relies on the viscosity validation. The viscosity validation is achieved when the SACF reaches a monotonic decaying trend.

Comparison

The outcomes of this study are comparable to the study of CuO nanoparticles diffusion in water system as investigated by Loya et al. [27]. It is found that the metal oxide nanoparticles give similar diffusion rate when diffused in water. As shown in Table 1, in both cases, water diffusion coefficient is lower than the CuO–water system and CeO2–water system since nanoparticle enhances the random motion of atoms in the system.

Table 1 Diffusion coefficients of CeO₂ and CuO nanoparticles in water system

Furthermore, the viscosity analysed using MD is within 5 % of discrepancies to experimental obtained values, which can be seen from Fig. 2. Nevertheless, these discrepancies are caused due to the velocity random seeding of the temperature fluctuation. During the system equilibration process, the pressure fluctuation can also be a part of causing discrepancies between MD and experimental values.

The standard error for diffusion of the CeO₂–water system was calculated to estimate the accuracy for the results obtained from simulation as shown in Table 2. The standard error was calculated by dividing the simulation time steps into 10 blocks. Later at each block, diffusion coefficient was calculated. It was found that the results of average diffusion were around 1.5E−8 m²/s for 10 blocks and the overall standard error was found to be about 30–33 %.

Table 2 Percentage of standard error for diffusion coefficients of CeO2 nanoparticles in water system

Conclusion

In the present work, MD method was used to simulate nanoparticle dispersion at an atomistic level in aqueous solution. The cerium oxide (CeO2) nanoparticles were chosen as a model because this metal oxide nanoparticle has several important applications, such as fuel cell electrolyte, catalyst, polishing materials, insulators, gas sensor, and UV blockers.

However, the study demonstrated high concurrent trends in contrast to the experimental study with discrepancies of 5 % between both studies. Although we have used a small size and small number of nanoparticles, it shows advancement in understanding nanoparticles aggregation and dispersibility at atomic level. Moreover, this study is necessary for the development and achieving initial parameters for further implementation on future simulations for various nanoparticles–fluid systems.