A Complementary Engineering-Based Building Damage Estimation for Earthquakes in Catastrophe Modeling

Abstract

Catastrophe modeling for earthquakes is conventionally designed as a probabilistic model to estimate the losses based on risk and vulnerability of a portfolio of exposures for a foreseeable set of events. This approach lacks a physical science of building damage that is linked to ground-shaking characteristics. A proposed engineering-based building damage estimation model based on established theories of seismic wave propagation and structural resonance is presented to address some of these shortcomings. A damage factor is introduced to provide an indication of the relative extent of damage to buildings. Analysis based on the proposed methodology is carried out using data derived from four case studies: the 2011 Tohoku earthquake; the 2007 Bengkulu earthquake; the 2011 Christchurch earthquake; and the 1999 Chi-Chi earthquake. Results show that the computed damage factors reasonably reflect the extent of actual damage to buildings that was observed in post-earthquake reconnaissance surveys. This indicates that the proposed damage simulation model has a promising future as a complementary assessment tool in building damage estimation in catastrophe modeling.

1 Introduction

Catastrophe modeling has conventionally been designed as a probabilistic model that estimates losses based on risk and vulnerability of exposure units for a foreseeable set of events. Factors affecting the estimates of losses of an exposure unit include site location, physical characteristics, and the financial terms of insurance coverage. Site locations are denoted as geocoding data such as street address, postal code, and country/CRESTA (Catastrophe Risk Evaluating and Standardizing Target Accumulations) zone. Physical characteristics describe the construction, occupancy status, year built, and number of stories of the building. Financial terms refer to the value, limit, and deductible of the coverage. In the case of earthquakes, a probable earthquake magnitude is simulated based on a catalogue of historical records of earthquakes within the region of concern. The next step is to estimate the Modified Mercalli Scale Intensities (MMI) of the region according to the distance from the quake’s epicenter, the focal depth and magnitude of the earthquake, and the geological structures at the location. Often these factors are accounted for with empirical attenuation equations for each geological structure. Different attenuation equations for each geological structure are needed to consider their differences in seismic wave propagation characteristics. Softer sediment would tend to amplify shaking, but would affect a smaller radius to the epicenter. Hard sediments or rocks experience lower shaking intensity, but the shaking can be felt at much larger distances from the epicenter. The MMI is thereafter correlated to the building physical characteristics and financial terms to estimate the damage losses. Different building physical characteristics yield different sets of vulnerability curves. This methodology is highly suitable for quantifying losses over a wide area or for portfolios with large number of buildings. Precise building damage estimation is often not the prime concern.

From an engineering perspective, some shortcomings exist in the conventional catastrophe modeling approach. Firstly, most conventional catastrophe modeling uses attenuation equations for different geological structures, but the variability of soil profiles is often much higher. Hence, the attenuation equations are often insufficient to give reasonable estimates of the seismic wave propagation in the soil. Secondly, damage prediction is usually dependent on the usage of the building in conventional catastrophe modeling, rather than the structural features of the building. For instance, a domestic building and a commercial building with identical structural properties located on an identical ground profile may yield different levels of structural damage because of a difference in vulnerability curves. Thirdly, the estimates of earthquake impact on the built environment in conventional catastrophe modeling relies on the magnitude of the earthquake in terms of energy dissipation, rather than on physical ground motion characteristics such as acceleration amplitude, frequency, and duration of shaking.

On the other hand, detailed state-of-the-art engineering numerical simulation to quantify damage is rarely carried out for large portfolios of properties because this detailed analysis entails enormous amount of time and effort. Information about building floor plans, structural member joint connection detailing, material strength test, and soil investigation reports that is necessary to carry out such analysis often are limited or inaccessible. A balance has to be struck between precision and sophistication of engineering computation. A simplified deterministic approach in calculating an anticipated degree of damage to a building based on engineering fundamentals is therefore desirable, which thereafter may be easily translated into potential financial losses in a separate study.

The objective of this study is to propose a complementary approach to quantify the vulnerability of buildings to earthquake damage according to engineering principles without employing unnecessarily sophisticated computation. The approach is also intended to be easily carried out by non-engineering professions. The process is split into three parts: a geotechnical analysis; a structural analysis of the building; and the creation of the “damage factor.” In order to validate the reliability of the proposed methodology, case studies are presented to evaluate how well the results from the proposed method agree with the observed damage in the field following the earthquakes.

2 Underlying Principles

The proposed approach involves identifying building vulnerability to resonance effect due to earthquake shaking. Resonance occurs when the frequency of ground shaking coincides with the natural frequency of a building. In this circumstance, the building oscillates violently with maximum displacement of the building relative to the ground. If the building is not ductile enough to accommodate the displacement, cracks on the building will develop and propagate through critical structural members. In extreme cases, the building may collapse due to loss of support from damaged structural members. The susceptibility to resonance depends on the fundamental frequencies of the ground and building.

2.1 Fundamental Frequency of Soil

The fundamental periods of a linear or equivalent linear soil profile can be obtained using simplified procedures (Dobry et al. 1976). If shear waves travel vertically with uniform shear wave velocity through a homogeneous soil profile that overlies a rigid bedrock, the predominant period of vibration of the soil, T, can be computed with Eq. 1:

$$ T = \frac{4H}{{v_{\text{s}} }} $$

(1)

where H is the thickness of soil layer, and v _s is the shear wave velocity. The period of vibration is a reciprocal of frequency (that is, f = 1/T). Soil deposits, having a fundamental frequency of its own, will influence the seismic response of the structures. Seismic waves are modified when they propagate through the soil strata as resonance between the soil strata and the seismic waves, which will amplify certain frequencies.

Although Eq. 1 is only applicable to cases where homogeneous soil is encountered, closed form solutions for various site conditions other than a homogeneous soil profile were also presented in the study conducted by Dobry et al. (1976), and a few approximate methods to evaluate the fundamental period of a layered soil deposit were also discussed. In general, the fundamental period, or the natural frequency of the soil profile, is a function of the shear wave velocity.

2.2 Fundamental Frequency of Building

The American Society of Civil Engineers (ASCE) provides a simple and straightforward empirical formula for fundamental frequencies of buildings in SEI/ASCE 7-05 (ASCE 2005). The formula is developed based on real data obtained from instrumented buildings that underwent ground motions during earthquakes such as the San Fernando and Northridge earthquakes. The data were used to obtain upper-bound and lower-bound equations from regression analysis; the formula provided in ASCE is the lower-bound equation and is intended to provide a conservative (shorter period) estimate. Shorter building periods result in higher base shears and therefore are more conservative (Jacobs 2008). The fundamental period (T _a) of a building can be approximated using Eq. 2:

$$ T_{\text{a}} = C_{\text{t}} H_{\text{n}}^{x} $$

(2)

where T _a is the approximate fundamental period and H _n is the height of building from the base to the highest level of the building in feet. C _t and x are coefficients obtainable from ASCE 7-05. A more precise estimate of fundamental period or natural frequency of buildings can be obtained with the use of modal analysis, which is available in commercial building software programs. For simplicity, the empirical formula from the ASCE indicated above in Eq. 2 is employed.

2.3 Displacement Amplification Ratio

When the frequency of the ground shaking and the building’s natural frequency coincide, resonance occurs. The building can be regarded as a single degree of freedom oscillator and a critical damping ratio (ζ) of 5 % is assumed. The harmonic response due to base excitation can be represented with the classic harmonic response of a linear second-order system expressed in Eq. 3:

$$ \frac{Y}{X} = \frac{1}{{\sqrt {\left\{ {\left. {\left[ {\left. {1 - \left( {\omega /\omega_{\text{n}} } \right)^{2} } \right]} \right.^{2} + \left[ {2\zeta \left( {\omega /\omega_{\text{n}} } \right)} \right]^{2} } \right\}} \right.^{ } } }} $$

(3)

where Y/X is the amplification ratio relative to the base displacement, and ω/ω _n is the normalized frequency between the ground base shaking and building natural frequency. Figure 1 shows the displacement amplification with different damping ratios. With a given normalized frequency for a particular building and location, the amplification of the building vibration relative to the ground shaking is obtained from the figure and will be utilized in the proposed damage prediction method.

Fig. 1

Displacement amplification ratio with normalized frequency

3 Basis of Proposed Damage Prediction

In order to translate the above underlying principles into a damage assessment tool, a site response analysis encompassing the wave propagation of seismic waves and fundamental frequency of soil is implemented. To account for the nonlinear soil response, an equivalent linear approximation is employed. Next the propagated waves would be compared with the natural frequency of the building to ascertain the amplification of the shaking on the building. Lastly, the displacement of the building due to the shaking would be translated into a “damage factor” to estimate the relative damage to the building based on wavelet analysis.

3.1 Equivalent-Linear Model for Site Response Analysis

Based on past earthquakes, the ground motions on soft soil sites were found to be generally larger than those of nearby rock outcrops (Idriss and Seed 1968). These amplifications of soil site responses were simulated using several computer programs such as SHAKE (Schnabel et al. 1972). The SHAKE program computes the site response of horizontally layered soil-rock profile subjected to transient and vertical travelling shear waves based on the wave propagation solutions of Kanai (1951), Roesset and Whitman (1969), and Tsai and Housner (1970). Cyclic soil behavior is simulated using an equivalent linear model, which is commonly adopted in geotechnical earthquake engineering applications (Idriss and Seed 1968; Kramer 1996). One of the latest versions of SHAKE, which considers frequency-dependent equivalent strain, is SHAKE91 (Idriss and Sun 1992; Sugito 1995). In my study, a similar site response algorithm proposed by Bardet et al. (2000) is used.

3.2 Equivalent Linear Approximation of Nonlinear Stress–Strain Soil Response

The equivalent linear model adopted in this study is based on a Kelvin-Voigt model. The shear stress τ depends on the shear strain γ and its rate $\dot{\gamma }$ as expressed in Eq. 4:

$$ \tau = G\gamma + \eta \dot{\gamma } $$

(4)

where G is shear modulus and η the viscosity. In a one-dimensional shear beam column, the shear strain and its rate are defined from the horizontal displacement u(z,t) at depth z and time t as follows:

$$ \gamma = \frac{\partial u(z,t)}{\partial z} $$

(5)

$$ \dot{\gamma } = \frac{\partial \gamma (z,t)}{\partial z} = \frac{{\partial^{2} u(z,t)}}{\partial z\partial t} $$

(6)

The equivalent linear shear modulus, G is taken as the secant shear modulus G _s measured at the ends of the hysteretic stress–strain curve during cyclic loading:

$$ G_{\text{s}} = \frac{{\tau_{\text{c}} }}{{\gamma_{\text{c}} }} $$

(7)

where τ _c and γ _c are the peak shear stress and strain amplitudes of each hysteretic stress–strain loop, respectively. Typical values of G _s and ζ with respect to γ can be found in several places in the relevant literature (Hardin and Drnevich 1972; Seed and Idriss 1970; Seed et al. 1986; Sun et al. 1988).

3.3 One-Dimensional Ground Response Analysis

The one-dimensional equivalent linear site response analysis is outlined in Fig. 2. A vertically propagating harmonic shear wave through a one-dimensional layered system can be expressed with the one-dimensional equation of motion:

$$ \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}\, = \,\frac{\partial \tau }{\partial z} $$

(8)

where ρ is the unit mass of the soil in any layer. Assuming the soil behaves as a Kevin–Voigt solid, Eq. 8 can be expressed as:

$$ \rho \frac{{\partial^{2} u}}{{\partial t^{2} }} = G\frac{{\partial^{2} u}}{{\partial z^{2} }} + \eta \frac{{\partial^{3} u}}{{\partial z^{2} \partial t}} $$

(9)

Fig. 2

One-dimensional layered soil deposit system (after Schnabel et al. 1972)

3.4 Iterative Approximation of Equivalent Linear Response

As discussed earlier, the equivalent linear model assumes that the shear modulus (G) and damping ratio (ζ) are functions of shear strain amplitude. In order to achieve the level of strain induced, the equivalent linear analysis is repeated with values of G and ζ until a compatible strain is produced in all soil layers. Analysis in this study showed that 8 iterations are sufficient to achieve convergence, similar to the suggestion in SHAKE (Schnabel et al. 1972).

3.5 Application to Damage Prediction

The objective of site response analysis is to determine the ground motion directly under a building. An earthquake scenario is presented in Fig. 3. Seismic waves are generated and propagated from the focus of the earthquake. The propagation of seismic waves in the form of primary, shear, Rayleigh, and Love waves is a complex phenomenon. Given the importance of shear waves to building damage, emphasis is placed on the effects of shear waves in this study. In Fig. 3, shear waves propagates vertically from the bedrock to the ground surface through the soil strata, which is subjected to damping and amplification effects depending on the geological properties of each soil layer. This surface ground shaking is picked up by the seismic measuring station on the left of the figure some distance away.

Fig. 3

Seismic wave propagation

In many cases, the recording of surface ground shaking (usually in the form of acceleration versus time) is the only quantitative information about earthquake shaking. With the knowledge of the soil profile beneath the measuring station, one can carry out an equivalent linear back-analysis to obtain the outcrop bedrock shaking. Assuming no energy loss in the bedrock within close proximity, this bedrock shaking beneath the measuring station can be taken as the bedrock shaking beneath the building shown on the right of Fig. 3. Such practice is commonly adopted in earthquake geotechnical engineering. Thereafter, a forward wave propagation analysis based on the equivalent-linear theory discussed earlier is conducted to obtain an estimate of the ground surface shaking at the building location based on the soil profile beneath the building. Soil profiles can typically be found in soil investigation reports produced by building consultants prior to the construction of the building.

Having obtained the acceleration time history of the ground shaking at the building location, comparison with the characteristics of the building is required to estimate the likely damage. As discussed earlier, resonance occurs when the ground shaking and a building’s natural frequencies coincide. This is the juncture where the building oscillates and displacement is large. In order to visualize the frequency content of the ground shaking, Fast Fourier Transform (FFT) analysis can be carried out to depict the ground shaking in the frequency domain as shown in Fig. 4. In a FFT analysis, the dominant frequencies of the earthquake shaking can be observed from the amplitude peaks. In Fig. 4, a wide range of frequencies are present, particularly the lower frequency contents as depicted with higher amplitudes between 0 and 3 Hz. There is also a dominant frequency at about 4.2 Hz, represented by a distinct peak in the same figure. Therefore, buildings with natural frequency of 4.2 Hz would be susceptible to resonance.

Fig. 4

Ground motion characteristics at Sendai TKY007 station during the 2011 Tohoku Earthquake. a Measured acceleration time history. b Fast Fourier Transform

3.6 Validation of Site Response Algorithm

In order to validate the proposed site response algorithm, two simulations are carried out to identify the fundamental frequency of a layer of soil of known thickness and shear wave velocity. In each of the simulations, a 10 m thick layer of soil of uniform shear wave velocity is subjected to a simple harmonic sinusoidal wave sweep motion from 1 to 20 Hz at the bedrock surface as shown in Fig. 5. The amplification of the input motion observed at the surface of the soil layer in the simulation signifies the fundamental frequency of the soil profile. From the simulation, a soil layer of 40 m/s gave a prominent peak at a frequency of 1 Hz, while the soil layer of 200 m/s produced a prominent peak at 5 Hz as shown in Fig. 6. These frequencies are analogous to the approximate values of fundamental frequency computed with Eq. 1, and confirm the reasonable accuracy of the site response algorithm adopted. There also could be significant second and third mode of vibration represented as the lower amplitude peaks shown in Fig. 6b. To anticipate the complexity of layered soil profiles in realistic field conditions, the complete acceleration time history of the ground motion should be considered rather than merely adopting the most prominent frequency in the proposed analysis.

Fig. 5

Input sinusoidal wave sweep from 1 to 20 Hz at bedrock

Fig. 6

Amplification of input motion at the surface of soil. a Soil with shear wave velocity of 40 m/s. b Soil with shear wave velocity of 200 m/s

3.7 Development of Wavelet-Based Damage Estimation

A peak amplification is produced when the normalized frequency is 1.0 (that is, ground shaking frequency equals the natural frequency of the building) as shown in Fig. 1. When this happens, a maximum displacement of the building can be expected due to resonance. In actual cases, soil-structure interaction exists and would alter the normalized frequency when the building is swaying during the earthquake. Such soil-structure analysis is complex for non-engineering professions and hence omitted for simplicity.

A building subjected to several cycles of shaking at resonance would expect more damage than one with only one or two cycles at resonance. However, this duration effect cannot be captured in the amplification or FFT plots. An alternative methodology is required to capture both effects of the frequency and time of earthquake shaking. Wavelet analysis is therefore proposed as an attempt to depict a more holistic response of a given building. Figure 7 shows an example of the wavelet plot. The vertical axis indicates the FFT amplitude of shaking, while the horizontal axes refer to the frequency and time units. The wavelet allows one to visualize the time when resonance occurs for a given building natural frequency. In order to estimate the shaking amplification throughout the entire earthquake, each data point on the wavelet has to be correlated to the displacement amplification graph in Fig. 1 to obtain the building amplification ratio relative to the ground shaking. The amplification ratio is thereafter multiplied with the displacement of the ground shaking at that specific frequency and time before cumulating the values to obtain the total displacement of the building in the form of a “damage factor.” This damage factor is taken as a qualitative degree of damage based on an assumption that the total displacement of a building due to resonance is proportional to the expected degree of damage. In order to facilitate the computation, a program code is written that allows the computation to be completed within a couple of seconds on a personal laptop computer. This methodology allows the resonance effect to be evaluated more holistically by considering the contribution of each frequency and also the duration of shaking. In the following case studies, the “damage factor” is compared with the observed damage of specific buildings impacted by each earthquake.

Fig. 7

Wavelet plot of ground shaking during the 2011 Tohoku Earthquake at measuring station TKY007

In order to assess the potential of the proposed methodology in quantifying expected building damage, case studies on historical earthquakes are presented. Buildings that underwent these earthquakes are selected and categorized according to a damage classification, adapted from the European Macroseismic Scale 1998 (EMS-98), as shown in Table 1. This classification acts as a benchmark for categorizing the extent of damage to a building observed in the field.

Table 1 Damage classification

To carry out the analysis with limited information, a number of assumptions have been made:

• (1) The soil profiles used in the case studies are gathered from various sources to the best of the author’s ability, and are assumed to be representative of the actual geological conditions at the site.

• (2) In-plane acceleration time history of ground motion that exhibits highest peak ground acceleration (PGA) at a measuring station is used in the analysis.

• (3) The focus of an earthquake typically occurs within the bedrock where tectonic faults are present. When performing site response analysis, it is assumed the bedrock acceleration outcropped from the nearest measuring station would be a close representation of the bedrock acceleration under these buildings. As distance of the building away from the measuring station increases, the bedrock energy loss is likely to be more apparent. Likewise, if the distance of two buildings to the measuring station is similar, the bedrock energy loss is deemed to be comparable.

• (4) The building layout is assumed to be regular such that the seismic response of the structure is similar in both principal directions. This limitation is due to limited information of building layouts. The responses of buildings with irregular layouts are often not as straightforward.

• (5) Only the fundamental mode of vibration of the building (that is, the first mode of vibration) is considered.

• (6) Equation 2 is representative of the natural period of the building.

4 Case Study I: 2011 Tohoku Earthquake, Japan

On 11 March 2011, a large magnitude 9.0 M_w earthquake occurred off the coast of the Tohoku region of the Pacific Ocean at a depth of 30 km. It was the largest recorded earthquake to have ever hit Japan and the fourth largest recorded earthquake in the world (USGS 2015). The mainshock was accompanied by several strong foreshocks and aftershocks in the range of M_w 6–7 (MCEER 2011). A large tsunami was also generated by the earthquake, which was responsible for the Fukushima Nuclear Power Plant meltdown.

The Japanese seismic monitoring system is advanced and complete with several measurement networks. In this case study, data are drawn from the K-NET and KiK Net system of the National Research Institute for Earth Science and Disaster Prevention (NIED 2011), which has over 1000 stations across the country. The seismic activity of the 2011 Tohoku earthquake was the strongest of the four case studies presented in this article with PGA values in excess of 2.7 g (NIED 2011). The major considerations for this seismic event are the number of aftershocks and the large tsunami event that followed the earthquake. These could potentially skew the extent of damage to buildings caused solely by ground shaking. To minimize this effect, buildings selected in this case study are located inland and unaffected by the tsunami and landslides. Because the magnitude of the mainshock earthquake was many orders larger than the aftershocks and foreshocks, it is assumed that the resonance damage to the building stock was largely caused by the mainshock. Details from three specific stations of the K-NET and KiK-NET network used in this case study are summarized in Table 2.

Table 2 Summary of stations used in the 2011 Tohoku Earthquake study

Since the early 1990s, Japan has enthusiastically embraced special seismic protection systems for buildings with over 2500 commercial and residential buildings with seismic isolation and 1000 with seismic dampening (SEAW 2011). This is arguably why most of the damage to buildings was due to the tsunami. New buildings, constructed in compliance with strict, modern Japanese building codes and seismic protection were largely unaffected. Of 634 public apartment blocks in Sendai, 97.4 % of reinforced concrete (RC) box structured buildings suffered no damage, all pre-stressed RC boxed wall structures suffered no damage, and 72.5 % of RC ribbed structures experienced no damage (AIJ 2011). Figure 8 shows the locations of the four building sites selected for this case study.

Fig. 8

Locations of building sites in Japan overlaid on GoogleMap

The geological profiles of the seismic measuring stations are obtained directly from the NEID (2011), where borehole logs were documented with shear wave velocity values required for site response analysis.

4.1 Building Sites

• (1) Site T1 Tohoku University Building [38.2544°N, 140.8387°E] (Heavy Damage)

  This building is part of the Department of Civil Engineering and Architecture at Tohoku University and was constructed in 1969. After being damaged in the 1978 Miyagi earthquake, it was later retrofitted with seismic countermeasures in 2001. The nine-story RC building, however, suffered heavy damage to the bottom of four corner walls and a severe crack in the side shear wall (Motosaka and Mitsuji 2012). Data from the two borehole logs located underneath the Tohoku University (THU) building presented by Motosaka and Mitsuji (2012) are used. However, shear wave velocity measurements are not available. An empirical relationship between standard penetration test (SPT) blow count (N) values and shear wave velocity (V _s) based on Kiku et al. (2001) model was used. The SPT N value is determined by the number of blows of a 63.5 kg hammer falling at a height of 0.76 m required to drive a 50 mm diameter sampling tube into the soil by 300 mm at a given depth of soil.

  $$ V_{\text{s}} = 68.3N^{0.292} $$

  (10)

• (2) Site T2 Takasago Apartment [38.2719°N, 140.9650°E] (Moderate Damage)

  The fourteen-story apartment buildings were about 40 m in height and located in Sendai City about 3 km away from the MYG013 measurement station (EEFIT 2011). The tilted building produced a gap in excess of 1 m at the top adjacent to the adjoining building (Mitsuji et al. 2012). The soil profile and shear wave velocity data are obtained from Motosaka and Mitsuji (2012).

• (3) Site T3 Lions Tower Kotodai [38.2783°N, 140.8670°E] (None)

  The twenty-nine story residential Lions Tower Kotodai is 104 m tall and was constructed in 2009. No noticeable structural damage was reported following the earthquake. Given the close proximity to site T2 and the MYG013 station, the soil profile at the building was obtained by interpolating the two locations’ borehole data with their relative distances.

• (4) Site T4 Mode Gakuen Cocoon Tower [35.6916°N, 139.6971°E] (None)

  The Mode Gakuen Cocoon Tower in the Shinjuku District of central Tokyo is 204 m tall with 50 stories. During the earthquake, heavy swaying was reported although no structural damage was sustained (SEAW 2011). The soil profile is based on the measuring station TKY007 that is located in the same region as the Tower. The station is positioned about 2 km north of the building site and we assume that it is representative of the soil condition at the base of the Tower.

4.2 Validation of Equivalent-Linear Model for Seismic Wave Propagation

In order to assess the equivalent-linear model for seismic wave propagation, a comparison between the actual and computed ground shaking of a nearby measuring station is conducted. A complete analysis involving backward propagation of shear waves to obtain the bedrock acceleration at a measuring station site is carried out, and thereafter a forward propagation is calculated to obtain the computed ground shaking at another measuring station site based on the latter’s soil profile. Under ideal situations, the computed ground shaking should be identical to the actual recorded shaking at the latter’s station. But as the equivalent-linear method is a simplified approach, some differences are expected.

A measuring station (FSK019) about 80 km away from Sendai’s MYG013 station is used in the validation. Figure 9 shows the recordings of ground motion of the mainshock event at FSK019 and the outcropped accelerations at its bedrock using backward wave propagation analysis as described earlier.

Fig. 9

Ground motion recording at FSK019 station during the Mw 9.0 mainshock event. a At ground surface of measuring station FSK019. b Outcropped bedrock acceleration beneath FSK019. c Actual measured bedrock acceleration beneath FSK019

Because FSK019 is a KiK-NET station with specialized seismograph at its bedrock directly beneath the station at depths exceeding 100 m, comparison between the outcropped bedrock acceleration (Fig. 9b) can be compared directly with the actual measured values shown below in Fig. 9c. Some slight discrepancies are expected due to the simplicity of the equivalent-linear method. The computed PGA is 0.76 m/s² while the measured PGA in the field was 0.78 m/s² (difference of 3 %). Nevertheless, both signatures of the acceleration time histories are similar and shown to be capable of providing a reasonable approximation of bedrock acceleration.

Using the computed bedrock accelerations obtained in Fig. 9b, a forward wave propagation analysis is carried out using the soil profile at another measuring station MYG006. The ground surface acceleration obtained is thereafter compared with the measured readings at MYG006. Results also showed similar signatures with a slight difference in PGA of 12 % (computed PGA of 0.591 m/s² vs. measured PGA of 0.53 m/s²). This is expected as the proposed method ignores bedrock energy dissipation over the 80 km distance between FSK019 and MYG006. The computed PGA at the ground surface is therefore higher than the measured value as observed. In view of the above findings, the suitability of the equivalent-linear method for wave propagation analysis is validated and recommended for the assessment of buildings located closest to the measuring station.

Out of the four selected buildings in this case study, sites T1 (Tohoku University Building), T2 (Takasago Apartment), and T3 (Lions Tower Kotodai) were located in Sendai. Site T4 (Mode Gakuen Cocoon Tower) was located at Tokyo. The nearby measuring station used to obtain the bedrock acceleration for sites T1, T2, and T3 is MYG013. The measuring station used for site T4 is TKY007. The ground surface acceleration for each site is computed based on their nearby borehole log data in a similar procedure to the earlier validation of the equivalent-linear method for seismic wave propagation. Thereafter, the computed ground surface acceleration is further analyzed with the wavelet approach.

4.3 Results and Discussion

Figure 10 shows the ground motion wavelet plot near site T1 during the 2011 Tohoku earthquake. Dominant frequencies are observed to be within the range of about 1.0–1.8 Hz between 47 to 50 s and 90 to 100 s of the earthquake time history. Hence, buildings with natural frequencies near these dominant peaks would be expected to suffer more damage at those time intervals of the earthquake. Similar analyses are carried out for the other selected building sites. Table 3 shows the characteristics of the buildings and their computed damage factors.

Fig. 10

Wavelet plot of ground shaking near the Tohoku University building (site T1)

Table 3 Building characteristics and damage factors for the 2011 Tohoku Earthquake

Based on the above analysis, the Tohoku University Building has the largest damage factor and is likely to suffer the most damage as compared to the rest of the sample buildings. This is logical as its natural frequency falls within the dominant frequencies of the ground shaking in Fig. 10. As the natural frequency of buildings leave the range of dominant ground shaking frequencies, the damage factors diminish as demonstrated by the data for Takasago Apartment and Lions Tower Kotodai. Because the Lions Tower Kotodai was recently built, its seismic resilience is superior to buildings constructed under older, less rigorous building codes. Older buildings, such as the Tohoku University Building and Takasago Apartment, were constructed prior to the major seismic code revision following the 1995 Kobe earthquake and hence were more prone to structural damage in the 2011 Tohoku earthquake. Mode Gakuen Cocoon Tower in Tokyo experienced seismic energy that was attenuated over the 300 km distance from the earthquake epicenter. This expectation is supported by the lower PGA measurement at TKY007 and therefore similar magnitude events are not likely to affect modern buildings in Tokyo. This is evident based on the low damage factor obtained from the analysis as shown in Table 3.

5 Case Study II: 2007 Bengkulu Earthquake, Indonesia

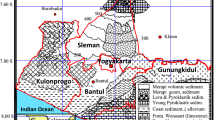
On 12 September 2007, a large megathrust earthquake (8.5 M_w) occurred off the west coast of Sumatra, 130 km SW of the city of Bengkulu. This quake was closely followed by two subsequent aftershocks registering a 7.9 and 7.0 M_w (Ambikapathy et al. 2010). There was only one measuring station in the vicinity of the earthquake. That station is located on the island of Pulau Sikuai (Fig. 11); the peak ground acceleration measurements for the main event and the two aftershocks are provided in Table 4.

Fig. 11

Locations of measuring station and epicenter of earthquakes overlaid on GoogleMap

Table 4 Measured peak ground accelerations (PGAs at Sikuai Station)

An estimated 25 people were killed with over 50,000 buildings damaged or destroyed. The tremors were felt across the island of Sumatra, although the most heavily damaged areas were towns along the coastline and the cities of Padang and Bengkulu. This seismic event in Indonesia was chosen because of its geographical location in Southeast Asia and the construction culture in a developing country. Other case studies cover the Asia–Pacific region and focus on the more developed countries. Despite these 2007 earthquakes being oceanic seismic events, they did not generate a major tsunami, and therefore provide a suitable context for assessing building damage in which ground shaking is the primary cause. One major consideration for the 2007 Bengkulu earthquake, however, is the occurrence of follow-up aftershocks that were of significant magnitude and may adversely affect the damage calculations. Given the narrow time interval of the aftershocks (less than a day), it is not possible to separate their impact on the same clusters of buildings in the region. It is therefore assumed that the total building damage can be described as a superimposing of damage factors from each event.

Following the earthquake, it was reported that many multistory reinforced concrete frame buildings with masonry infill in the cities of Bengkulu and Padang suffered cracking, but little structural damage was observed (Han et al. 2012). Due to the limited soil profile information in Bengkulu, emphasis is placed on buildings in Padang City, which is approximately 20 km away from the Pulau Sikuai measuring station. Figure 12 shows the location of the buildings in Padang City.

Fig. 12

Map of Padang with building site locations overlaid on GoogleMap

Due to the absence of geological data under the measuring station at Pulau Sikuai, an estimate based on shear wave profiling measurements at the city of Padang at 20 km away is attempted. Relying on Han et al.’s (2012) 3D shear velocity structure for Padang City, an extrapolation was carried out to estimate the soil profile at the Pulau Sikuai station. In the case of the four selected buildings (B1–B4), their soil profile is obtained through interpolation of Han et al.’s (2012) 3D shear velocity structure.

5.1 Building Sites

• (1) Site B1 Hyundai Shophouse [0.9374°S, 100.3544°E] (Complete Collapse)

  The Hyundai Shophouse was one of the low-rise RC buildings in Padang that suffered complete structural failure (EERI 2007). The building was two-stories high and constructed with RC columns, slab roof, and floors.

• (2) Site B2 Plaza Andalas [0.9496°S, 100.3541°E] (Moderate Damage)

  The Plaza Andalas was a four-story RC building, which suffered light structural damage (Hausler and Anderson 2007). Cracking of the exterior nonstructural masonry cladding was observed.

• (3) Site B3 Mosque [0.9551°S, 100.3587°E] (Moderate Damage)

  A two-story mosque located next to Bumiminang Hotel also suffered severe cracking on the nonstructural members, which did not compromise the overall structural integrity of the building (Hausler and Anderson 2007).

• (4) Site B4 Telkom Building [0.9264°S, 100.3670°E] (Light Damage)

  This four-story RC building in central Padang suffered similar damage to site B2 where severe cracking was observed on the exterior cladding (Hausler and Anderson 2007). Structural damage was minor.

5.2 Results and Discussion

Figure 13 depicts the measured ground acceleration time history of the mainshock, aftershock I, and aftershock II at Pulau Sikuai. Despite a lower moment magnitude, the M_w 7.9 event (aftershock I) produced a larger PGA than the M_w 8.5 mainshock (12.16 vs. 3.92 m/s²). The difference in PGA is largely due to the further distance of the epicenter of the mainshock to Pulau Sikuai. In addition, the two measurements of earthquake size differ. The moment magnitude scale is a measure of the size of earthquakes in terms of energy released. The PGA is a measure of earthquake acceleration on the ground. Given the relevance of violent ground motion to building damage, earthquake engineers often rely on the latter to give a better estimate of building response and damage. Modern catastrophe modeling often still relies on energy-based earthquake magnitude scales for ease of convenience. The ground attenuation obtained through these energy-based earthquake measurements may further reduce the accuracy of damage losses and therefore result in more risk in the pricing of insurance policies. The lowest PGA of the three events is the M_w 7.0 event, which registered 1.47 m/s². Following the same process as the earlier case study on the Tohoku earthquake, the bedrock accelerations are obtained and subsequently used to determine the expected ground motion at the four Padang building sites.

Fig. 13

Measured ground acceleration time histories at Pulau Sikuai. a Mainshock. b Aftershock I. c Aftershock II

The wavelet analysis is conducted and damage factors obtained for all three events are tabulated in Table 5. Site B1 gives the largest total damage factor, which is in agreement with field observations. Sites B2, B3, and B4 produce lower and fairly similar damage factors, indicating comparable degree of building damage. This is supported by the light damage of these buildings observed in the field. Aftershock I produced the highest damage factor out of the three events for all buildings. This indicates that aftershock I is likely responsible for the bulk of building damage observed in the field rather than the mainshock.

Table 5 Building characteristics and damage factor for the 2007 Bengkulu earthquake

5.3 Comparison with Conventional Attenuation Models

A brief comparison between the use of the proposed engineering-based approach and the conventional empirical-based attenuation model approach is carried out. The latter is based on a report by Aydan et al. (2007), which applied attenuation models to estimate the PGA contours radiating from the epicenters of the M_w 8.5 mainshock and M_w 7.9 aftershock. Table 6 shows the comparison of the two approaches. Results show that the PGA differences between the proposed approach and attenuation estimates are comparable for all building sites except B2 for the M_w 7.9 aftershock. In the case of the M_w 8.5 mainshock, the PGAs of the two approaches vary quite significantly, between 42 and 63 % difference. At the Pulau Sikuai station site, the attenuation approach gave a two times or greater difference in PGA when compared with the measured values for the M_w 7.9 aftershock and M_w 8.5 mainshock respectively. Unfortunately, the proposed approach is unable to produce an estimate of the PGA at the Pulau Sikuai station, since it is taken as a reference measuring site. Although there is lack of an alternate measuring station to verify the proposed approach in this case study, a similar validation of seismic wave propagation has been demonstrated in the earlier Tohoku earthquake case study.

Table 6 Comparison of PGA between the proposed approach and attenuation estimates

6 Case Study III: 2011 Christchurch Earthquake, New Zealand

A moment magnitude M_w 6.3 earthquake struck Christchurch, New Zealand on 22 February 2011. Christchurch is New Zealand’s third most populous city with a pre-earthquake population in excess of 330,000 people. The majority of residential housing consists of wooden/brick houses ranging from 1 to 2 stories high. The central business district (CBD) has a combination of restored nineteenth century masonry buildings and modern high rise buildings (Statistics New Zealand Tatauranga Aotearoa 2013).

Prior to this earthquake, Christchurch experienced a 7.1 magnitude earthquake in September 2010 that caused little damage and no fatalities. But the previous earthquake may have weakened several buildings and made them more susceptible to the February 2011 earthquake. For simplicity, it is assumed that the September 2011 earthquake had no effect on the buildings involved in the following calculations. Five buildings are selected for analysis. Additionally, the measurement stations used in the study are shown in Fig. 14.

Fig. 14

Locations of building sites and measuring stations in Christchurch overlaid on GoogleMap

6.1 Building Sites

• (1) Site C1 Christchurch Cathedral [43.5310°S, 172.6371°E] (Complete Damage)

  Christchurch Cathedral is arguably one of the most iconic landmarks in the city. Built in the 19th century from masonry, the 62.5 m tall structure consists of a spire and a nave. The 63 m tall spire suffered from a total collapse during the earthquake (New Zealand Herald 2011a).

• (2) Site C2 CTV Building [43.5328°S, 172.6424°E] (Complete Damage)

  The Canterbury Television (CTV) building collapse was single-handedly responsible for the most fatalities out of all the structural damage caused by the 2011 earthquake. In total, 115 people were killed when the six-story concrete structure effectively “pancaked” upon itself (New Zealand Herald 2011b). The structural design was not out of the ordinary consisting of a system of shear walls, reinforced concrete columns, and a steel framed roof. An investigation by the Canterbury Earthquake Royal Commission (2012) revealed that although the legal building standards were largely adhered to, the standard of “best practice” was judged to have been lacking in certain areas.

• (3) Site C3 Grand Chancellor Hotel [43.5328°S, 172.6390°E] (Moderate/Heavy Damage)

  The Grand Chancellor Hotel was the tallest building in Christchurch at the time of the earthquake standing at 85 m with 26 stories. It was unaffected by the 2010 earthquake, but during the February earthquake the hotel suffered severe structural damage caused by the collapse of a shear wall (New Zealand Department of Building and Housing 2011). The structural damage is classified as moderate/heavy owing to the fact that the structure is still standing and the only visible damage being a slight lean.

• (4) Site C4 TVNZ Building [43.5301°S, 172.6413°E] (Heavy Damage)

  Another building located in the CBD area of Christchurch, the Television New Zealand Christchurch (TVNZ) building was a four-story, 15 m tall structure consisting of mainly reinforced concrete members. Earthquake damage includes the collapse of side walls and cracking of internal members, although structural integrity was maintained. The building was ultimately demolished (TVNZ 2011).

• (5) Site C5 Residential House [43.5106°S, 172.7324°E] (Light Damage)

  A two-story residential house is chosen to be a representative of the “green” land zone houses in Christchurch outside the CBD based on the damage category classification by the Canterbury Earthquake Recovery Authority (CERA 2014). There was a large variance in the extent of structural damage suffered by these types of houses from the earthquake. The majority of damage occurred was due to ground settlement or liquefaction of the soil. The selected house suffered light structural damage.

For analysis of buildings within the CBD, the soil profile taken at measuring station CHHC is assumed to be representative of soil underneath the entire CBD given the compact nature of the district (Storie and Pender 2013). In the case of the residential house (site C5) at a distance away, the soil profile used follows the nearby measuring station NNBS. The shear wave velocity profiles of the soil are obtained from a study by Wood et al. (2011).

6.2 Results and Discussion

Based on the results obtained from the analysis as shown in Table 7, a damage factor exceeding 8.9 in this case study appears to indicate complete collapse of the building. Lower damage factor values, but above 6.4, showed heavy damage based on field observation of the selected buildings. Similar to the earlier case studies on the 2011 Tohoku earthquake and 2007 Bengkulu earthquake, the analysis produced higher damage factors for more severely damaged buildings observed in the field.

Table 7 Building characteristics and damage factor for the 2011 Christchurch earthquake

7 Case Study IV: 1999 Chi-Chi Earthquake, Taiwan Island

On 21 September 1999, a magnitude M_w 7.7 earthquake occurred in Nantou on the island of Taiwan. The shaking lasted for approximately 40 s, which collapsed more than 10,000 buildings. Over 11,000 people died in the event, making it the second most deadly Taiwanese earthquake in recorded history (EQE 1999). The 1999 earthquake event was also subject to multiple aftershocks. In this case study, the analysis focuses only on the mainshock. The effects of aftershocks are omitted given the scarce data available. The building sites selected are located in regional metropolitan areas close to the epicenter of the earthquake around Wufeng, Nantou, Fengyuan, and Taichung.

Figure 15 shows a regional map of the earthquake area and the locations of selected building sites for the study. Five building sites close to the epicenter of the earthquake are chosen for analysis. Geological data are obtained from nearby borehole investigations and the earthquake accelerations are derived from two measuring stations. Analysis of sites CC1 and CC2 involve using TCU076, while sites CC3, CC4, and CC5 involve the TCU065 station. Details of these stations are provided in Table 8. In cases where shear wave velocities of the soil are absent for building locations, they are derived from empirical relationships between the number of blows of the Standard Penetration Test (SPT N) value and the shear wave velocity based on the Kiku et al. (2001) proceedings paper.

Fig. 15

Regional map of central Taiwan Island along the west coast and locations of selected building sites overlaid on GoogleMap

Table 8 Details of the measuring stations used in the 1999 Chi-Chi earthquake analysis

7.1 Building Sites

• (1) Site CC1 Residential Building [24.0657°N, 120.6992°E] (Heavy Damage)

  In the town of Dali, two five-story reinforced concrete buildings experienced a collapse of the first floor structural columns (GEER 1999). These buildings tilted away from each other and leaned against adjacent buildings across minor roads. High structural resonance accompanied with out-of-phase shaking between the two buildings was postulated to be the cause of the heavy damage.

• (2) Site CC2 Residential Building [24.11°N, 120.67°E] (Heavy Damage)

  A fifteen-story building in Taichung suffered partial collapse of the lower two floors, which resulted in the subsequent collapse of a portion of the entire apartment block. This is classified as partial structural collapse as only a portion of the building suffered damage (GEER 1999).

• (3) Site CC3 Warehouse Building [23.93°N, 120.67°E] (Heavy Damage)

  Similar to the first two building sites, an industrial warehouse in Yuanlin underwent structural collapse of the first floor, which resulted in the top floors pancaking and crushing the parked trucks below. No settlement or deformation of the ground was observed (GEER 1999).

• (4) Site CC4 Commercial Building [23.95°N, 120.60°E] (Heavy Damage)

  The building is a four-story RC structure located in Yuanlin approximately 15 km away from the epicenter of the earthquake. The structural failure is due to the collapse of the first story support (GEER 1999).

• (5) Site CC5 Residential Building [23.90°N, 120.69°E] (Light Damage)

  A seven-story building in the Nantou region. This residential building experienced little structural damage from the earthquake. But there were visible signs of cracking of superficial façades and cosmetic cladding (GEER 1999).

7.2 Results and Discussion

Table 9 shows the results of the analysis. According to the results from the proposed method, the highest damage factor indicates that site CC1 would undergo the largest total displacement due to resonance, and could expect the heaviest damage. Site CC5 has the lowest damage factor and would likely experience the least damage based on the proposed methodology. Both observations are in agreement with the actual building damage sustained in the field. Although the buildings at sites CC1 to CC4 failed by similar soft-story collapse, the damage factors portraying such failure vary between 93.99 and 407.40. In addition, despite some differences in damage factors between sites CC4 and CC5, they are not proportional to the large difference in observed damage in the field. Some discrepancies could be due to the lack of building information and irregularities of building layout. Site CC5 has a circular floor layout, which would have led to a less accurate estimation of building natural frequency in Eq. 1. In addition, the assumed soil profile obtained from nearby boreholes may not be representative of conditions directly beneath these buildings. Nevertheless, the general relationship of larger damage factor to probable building damage is confirmed, which indicates that the proposed methodology can be adopted confidently as a complementary assessment of building damage in catastrophe modeling.

Table 9 Building characteristics and damage factor for the 1999 Chi-Chi earthquake

8 Summary of Results

Table 10 summarizes the results from the four case studies presented. Looking at the damage factors, the relative damage between the buildings is reasonably well correlated in all case studies. The absolute magnitude of the damage factor varies across all four case studies; as a result the extent of damage cannot be predicted from the damage factor number alone, especially for the 2011 Christchurch earthquake. For instance, a damage factor of 400 would represent the category of “Heavy” damage to buildings for all case studies, except the 2011 Christchurch earthquake that showed a damage factor of 9 for complete collapse. There are several factors that could have led to this inconsistency:

Table 10 Results from the four case studies

• (1) The building codes vary from time to time and also differ from country to country, therefore the earthquake resisting ability of buildings differs. For example, site T3 has a high damage factor of 293. The extent of damage is negligible. On the other hand, a slightly higher damage factor of 341 for T2 yields a “Moderate” damage. This is likely attributed to the difference in building codes that these buildings followed at their time of construction.

• (2) The proposed method does not account for the direction of wave propagation, but uses the acceleration record that exhibits the largest PGA to quantify resonance effect. This would be a conservative estimation of the earthquake effect that buildings of different orientation may experience, so some damage factors produced may be an overestimation as a result.

• (3) The proposed method does not account for energy attenuation from seismic station to the building site. While working on each case study, the seismic stations are carefully selected such that the distance to the building sites is short. This “distance” fluctuates between a few kilometers to tens of kilometers across the four case studies.

Nevertheless, the proposed method has proven to be capable of predicting the relative resonance effect, and this is sufficient to be used as a complimentary assessment to conventional empirical catastrophe modeling. Further improvements can be made to scale the damage factor such that a damage category can be identified directly.