A comparison of four approaches from stochastic programming for large-scale unit-commitment

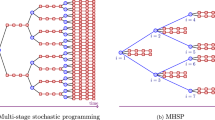
Abstract

In energy management, the unit-commitment problem deals with computing the most cost-efficient production schedule that meets customer load, while satisfying the operational constraints of the units. When the problem is large scale and/or much modelling detail is required, decomposition approaches are vital for solving this problem. The recent strong increase in intermittent, relative unforeseeable production has brought forth the need of examining methods from stochastic programming. In this paper we investigate and compare four such methods: probabilistically constrained programming, robust optimization and 2-stage stochastic and robust programming, on several large-scale instances from practice. The results show that the robust optimization approach is computationally the least costly but difficult to parameterize and has the highest recourse cost. The probabilistically constrained approach is second as computational cost is concerned and improves significantly the recourse cost functions with respect to the robust optimization approach. The 2-stage optimization approaches do poorly in terms of robustness, because the recourse decisions can compensate for this. Their total computational cost is highest. This leads to the insight that 2-stage flexibility and robustness can be (practically) orthogonal concepts.

Appendix: Didactic toy example

In this appendix we present a small example that may help the reader visualize the difference and similarities between the suggested models.

The set of assets consists of two thermal plants, subject to power limits and ramping rates. There are only two stages and time steps in the problem and only the load in the second time step, i.e. second stage, is uncertain (see Table 12 for further data).

Table 12 Characteristics of the toy example

The deterministic load is equal to $d = (0.75,0.75)$, and the second-stage load varies uniformly in the interval (0.25, 1.25). The bounds in (1) are $s^d = (0.0, -0.1)$, $s^u=(0.0,0.5)$. In what follows $p^1 = (p^1_1, p^1_2)$ will denote the production level of the first unit and $p^2 = (p^2_1, p^2_2)$ that of the second.

1.1 The deterministic approach

One can readily observe that the optimal solution is to use unit 1 only and produce (0.75, 0.5) for a total cost of 13.75. Note that the minimal stable generation of 0.5 prevents this unit from decreasing its production in the second stage further. Unit 2 remains offline.

1.2 The 2-stage approach

The situation is now rather different and partially depends on the possibility for us to switch off unit 1 in the second time step, when $d_2$ has been observed. If this can be done, unit 1 can still be online in the first time step. Then a feasible strategy is one wherein unit 1 produces 0.75 in the first time step and

• 1. if $d_2 < 0.4$, shutdown unit 1 and use unit 2 to generate 0.25 MW.

• 2. if $d_2 \in [0.4,1.0]$, unit 1 produces at MSG in the second time step

• 3. if $d_2 \in (1.0,1.25]$, unit 1 produces $d_2 - 0.5$ in the second time step.

One can readily compute that this solution leads to an expected cost of 15.3063. A second feasible solution is to only use unit 2. In this situation unit 2 produces 0.75 in the first time step and

• 1. if $d_2 < 0.75$, unit 2 generates 0.25 MW in the second time step.

• 2. if $d_2 \in [0.75,1.25]$, unit 2 produces $d_2 - 0.5$ in the second time step.

The expected cost is 15.6250, making this a suboptimal solution.

If unit 1 has to remain online in the second stage, the first strategy described above leads to an infeasible second-stage problem for several random realizations. Consequently only the second strategy remains feasible and hence optimal.

1.3 The probabilistically constrained approach

In this situation the probability constraint (3) becomes $\mathbb {P}[d_2 - 0.5 \le p^1_2 + p^2_2 \le d_2 + 0.1] \ge p$. For a given probability level of say $p=0.55$, we can observe that the probability request can be alternatively cast as the following linear constraint $0.3 \le p^1_2 + p^2_2 \le 0.8$. In this particular situation, the probabilistically constrained model is more demanding than the deterministic model, which requests $0.25 \le p^1_2 + p^2_2 \le 0.85$, but the difference is not seen on the optimal solution due to the MSG restriction on the first unit. The optimal solution is therefore to use unit 1 to generate $p^1=(0.75,0.5)$ and keep unit 2 offline.

1.4 The robust constrained approach

An uncertainty set $\mathcal {D}$ consistent with the above probabilistically constrained model would be $\mathcal {D} = \left\{ d \in R^2 \; : d_1 = 0.75, d_2 \in [\bar{d},\bar{d} + 0.55]\right\}$. With such an uncertainty set, the constraint (5) related to the second time step reads $\bar{d} + 0.05 \le p^1_2 + p^2_2 \le \bar{d} + 0.1$.

This leads to the following set of solutions:

• 1. For $\bar{d} \in [0.25,0.4)$, use unit 2 to produce 0.75 in the first time step and $\bar{d} + 0.05$ in the second time step. The cost of this solution lies in the interval [15.25, 16).

• 2. For $\bar{d} \in [0.4,0.45]$, use unit 1 to produce 0.75 in the first time step and 0.5 in the second time step. The cost of this solution is 13.75.

• 3. For $\bar{d} \in (0.45,0.7]$, use unit 1 to produce 0.75 in the first time step and $\bar{d} + 0.05$ in the second time step. The total cost lies in the interval [13.75, 14.50].

1.5 The 2-stage robust approach

Here the situation depends only on the given uncertainty set $\mathcal {D}$ and not on the flexibility of unit 1 as in the stochastic 2-stage approach.

Indeed, assuming that the first unit can be switched off in the second stage, then as soon as there exists $d \in \mathcal {D}$ with $d_2 < 0.4$, the worst-case cost of strategy 1 exhibited in the 2-stage stochastic approach is highly costly as it involves two starting costs (it is 23.5). Consequently only the second solution involving only unit 2 is retained. If unit 1 cannot be switched off, the solution strategy involving unit 1 is not even feasible.

However, as long as any $d \in \mathcal {D}$ has $d_2 \ge 0.4$ the first strategy is optimal, independently of whether or not unit 1 can be switched off or not.

1.6 A remark on comparing 2-stage and mono-stage approaches

Following the framework laid out in (8) both 2-stage approaches compute an optimal strategy that depends on various problem characteristics, but also a first-stage vision of the future (called x in (7)). For, the strategy involving unit 1 this vision would be $p^1 = (0.75,0.5)$, $p^2=(0,0)$. The strategy involving unit 2 would provide a first-stage vision $p^1=(0,0)$, $p^2=(0.75,0.25)$. Note that this first-stage vision can be compared with the solutions obtained from the mono-stage approaches and vice versa.