1 Introduction

The estimation of tree volume remains one of the most important tasks in forestry and forest research. In spite of the investment to develop estimation methods, assessing tree volume remains challenging, mostly because it can hardly be done directly on the field. Estimating the aboveground volume on large scale is usually done by applying allometric models established either on felled trees, using remote diameter measurements on standing trees, or more recently from laser scanning (Calders et al. 2015). However, such models are basically non-generic (strongly influence/dependent on the observations used to fit them) and should be applied with care to trees outside of the population used for the model’s fit. Indeed, changes in the silvicultural regime or ecological conditions proved to be very influential on tree allometry and result in biases for both total volume and its partitioning (Forrester et al. 2017). The sampling itself may have a great influence on the model’s fit, on the parameters and their confidence interval, and the residual variance (Cunia 1964). If generality is a desired property for a model, it is necessary to take all the “between stand” and the “within stand” variability sources into account for the equation building (Wirth et al. 2004). The great number of volume or biomass equation developed (e.g., Zianis et al. 2005 for temperate species, Henry et al. 2011 for tropical species, Chojnacky et al. 2014; Neumann et al. 2016) is a direct consequence of the fact that the equations have a limited geographic validity and have often been fitted on few trees. Taper equations can provide volume estimations and are based on measurement of diameters along the tree bole. Such models are therefore particularly sensitive to spatial variations in stem form and represent good indicators of the local errors that can result from applying allometric models outside of their base geographic domain. Inversely, including upper diameter measurements has been proved in many occasions to improve substantially the estimation of the volume thus making them more spatially robust (Kublin et al. 2013). Robust taper equations also require a local, site-specific or stand-specific calibration, for unbiased predictions.

The use of mixed-effect models contributed to improving the robustness of the models and reduce bias. They proved to have smaller prediction errors than fixed-effect models and were successfully utilized to do local calibration of allometric models, hence intrinsically have greater adaptability (Lappi 1986; Calama and Montero 2004; Adame et al. 2008; Cao and Wang 2011). The random parts of the models account for the hierarchical structure of the dataset whereby several trees are sampled from the same site, potentially violating the hypothesis of independence among observations—this represents the majority of samplings in the literature. The random effects also represent the geographic variation, generally a site-level or plot-level variation, and possibly nested in a larger regional or national level. Such models have been recently developed for their ability to provide predictions at different levels of the independent variables. However, the magnitude and the distribution of the random effects are very seldom reported and documented in the literature.

Predicting the random effects parameters for new levels can be made using local calibration, which requires the use of local measurements made on few trees, typically a small fraction of the number used to fit the model. Methods and limitations to the estimation of the random effects for predictions can be found in Ni and Nigh (2012). This calibration requires the estimation of the random effects parameters, which are not formally defined but for which different estimation procedures were proposed and have been successfully applied in different forestry applications (e.g., Hall and Bailey 2001; Cao and Wang 2011; Paulo et al. 2011). Yang and Huang 2011 Another possible calibration has been recently proposed and seems to produce superior fits, particularly when the dataset is small: the Bayesian calibration, which has been recently advocated (Zapata-Cuartas et al. 2012; Zell et al. 2014). We are aware that the local estimation of random effects is generally based on the empirical Bayes approach (Vonesh and Chinchilli 1997, Meng and Huang 2009), and thus, local estimation of random effects can be considered as a Bayesian estimation. But here, we refer to Bayesian calibration only for the situation where the model parameters are all fitted based on Bayesian models, which is done here within the Monte Carlo Markov Chain framework (MCMC).

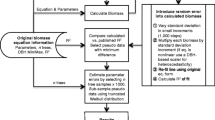
In order to test and compare the two calibration methods, the random effects parameters estimation or the Bayesian calibration, a taper model for Norway spruce (Picea abies L.) was fit from a detailed measurement campaign over Romania. The taper model was fit with random effects using two methods, maximum likelihood and Bayesian, then applied to trees sampled from sites not used for the fit and with different growing conditions, representing a difficult or risky extrapolation. Last, a Bayesian calibration based on fit statistics, not direct measurements, is implemented to test the potential of literature-based calibration where local data are not directly available.

2 Material and methods

2.1 The datasets

Two sets of data were used for the analysis: the first set, referred to as the fit dataset, was used to fit the models while the second set was used to perform their local calibration and validation.

2.1.1 The fit data set

The 16 plots were inventoried according to the National Forest Inventory procedure (Marin et al. 2010), and 3 to 10 trees per plot were selected for destructive measurements as a constant fraction of the total number of trees in the plot. The plots consisted in two concentric circles of fixed radius: 56 ≤ breast-height diameter (dbh) ≤ 285 mm within 0–7.98 m and dbh ≥ 285 mm within 0–12.96 m. Within each plot, tally trees are measured both in dbh, total height, base of living crown, and base of dead crown. Plots were dominantly set up on clear-cut areas (building road or electric lines) so that all tree size (in diameter and height) but particularly big trees could be sampled. Thus, the selection of the trees sampled was not limited by silvicultural constraints, which would otherwise have led to felling trees from lower canopy positions. Successive diameters (outside-bark) were measured along the stem using a caliper after felling at prescribed heights: 0.1, 0.5, 1, 1.3, 2, 2.6, and 3 m and then every 2 m to the tip.

The fit sample covered a range of dbh from 5.6 to 53.4 cm, and of total height from 1.3 to 41.6 m (Table 1).

Table 1 Comparison of the site and destructively sampled tree characteristics for the fit and evaluation datasets. Site ID; site name; elevation (m a.s.l.); stand density; age class; sampled trees; dbh range (cm); tree height range (m)
Full size table

2.1.2 The application set

Two high elevation stands were sampled in the buffer zone of forest reserves, thus differing from the stands used for the fit by their low-intensity (to no) forest management and a high elevation as compared to the fit set. The first site (47° 46′19″ N, 25° 48′ 70″) was located in the Rărau Giumalău Mountains at an elevation of 1350–1450 m on a slope of 25–35°. The second site (47° 19′ 02″ N, 25° 15′ 10″) was located at a similar elevation (1400–1500 m) and slope range, about 40 km apart from the first site.

At both sites, the application set was constituted of 24 trees covering the diameter range of the stands, from 6 to 66 cm, measured after felling. Two trees were sampled per diameter class in each stand so the application sets can be randomly split in two equally sized batches of trees (12 trees) having very similar dimensions: one batch was used for the local calibration and referred to as the calibration batch, the other for describing the fit quality and quantifying the impact of the calibration, referred to as the evaluation batch.

2.2 The stem taper equations

Many taper equations have been published, which differ both in their form and in the number of their parameters. Flexibility seems to have been an important aspect in the development of the different equations, based on variety of functions, from exponential to spline. Choosing the best suited taper equation could be a study on its own, given the great diversity of published equations: polynomial, variable-exponent (Kozak 1997), spline (Kublin 2003), continuous or segmented curves (Max and Burkhart 1976). Although very different in their shape and parametrisation, different models can have very comparable performance, particularly for smooth and regular stems such as that of spruce. As Arias-Rodil et al. (2015) put it, “none can be considered best.” The ultimate choice could have been based on comparing the third decimal of some statistics but the choice here was rather related to the possibility of including covariates and to the necessity to have a model addressing separately each stem portions explicitly.

Thus, the stem taper equation used in this study is a versatile equation successfully fit to a variety of species such as eucalyptus (Saint-André et al. 2002; Gomat et al. 2011) and teak (Adu-Bredu et al. 2008). Given the dbh and the total height of the tree (H), the equation relates the relative diameter dr (dr = d/dbh) to the relative height hr (hr = h/H) as:

$$ dr={a}_1\times \Big(\left(1-{a}_2\times hr\right)\left(1+{a}_3\times {e}^{-{a}_4. hr}\right)-\left(1-{a}_2\right)\times {hr}^{a_5} $$
(1)

This taper model has the advantage of having parameters specifically related to each of the main stem fractions: the stem taper (a1 and a2), the butt-swell and taper of the lower stem part (a3 and a4), and the stem top (a5).

This initial model was further developed by testing possible effects of covariables on the parameters of the model themselves (Adu-Bredu et al. 2008; Gomat et al. 2011). In our case, the model (1) was fit once on the fit dataset individually, i.e., separately for each tree, then the 126 set of parameters were correlated to candidate covariables: h/d, dbh, top height and a robustness index estimated as \( \raisebox{1ex}{$\sqrt{\left(\pi \bullet dbh\right)}$}\!\left/ \!\raisebox{-1ex}{$H$}\right. \). There was little evidence of correlation, except between a1 and tree height, ht. The form of the relationship was clearly non-linear, and while different forms were tested, a simple hyperbolic model seemed the most suited. This lead to the more complete model (2) derived from model (1) as:

$$ dr=\left({a}_1-\frac{a_2}{1+{a}_3}\right)\times \Big(\left(1-b\times hr\right)\left(1+c\times {e}^{-d. hr}\right)-\left(1-b\right)\times {hr}^e+\varepsilon $$
(2)

The model parameters for which a random site-level effect was included were the parameters b, c, and d. It was not possible to estimate random effects for all parameters because of computational issues despite the fair amount of available data (N = 1896). The model with random effects was in the form:

$$ dr=\left({a}_1-\frac{a_2}{1+{a}_3}\right)\times \Big(\left(1-{b}_2\times hr\right)\left(1+{b}_3\times {e}^{-{b}_4. hr}\right)-\left(1-{b}_2\right)\times {hr}^{b_5}+\varepsilon $$
(3)

with ∀ k ∈ [2, 4], bk = βk + vk,j where is the fixed part of the parameter βk, and vk,j is the random, site-level component such that for each site j, vk, j~N(0, σk2), and model’s residual ε~N(0,  σ2). The variance components σk2and σ2 are unknown and need to be estimated during the MCMC fit. Convergence cannot be achieved if b5 is expressed as a random-effect parameter. The final form of the model was chosen based on fit statistics for different combinations of parameters using the Akaike information criterion (AIC), the bias, the model efficiency (MEF), and a pseudo-R2. The bias, MEF, and pseudo-R2 were computed as:

$$ Bias=\frac{\sum {\left(y-\hat{y}\right)}^2}{n} $$
$$ MEF=1-\frac{\sum {\left(y-\hat{y}\right)}^2}{\sum {\left(y-\overline{y}\right)}^2} $$
$$ Pseudo-{R}^2= corr{\left(y,\hat{y}\right)}^2 $$

where y is the measured relative diameter, \( \hat{y} \) the predicted value, \( \overline{y} \) the mean value over all n observations. The comparison of the fit statistics for different model forms is displayed in Table 6 (Appendix).

Autocorrelation in errors caused by the use of several measurements per tree (Meng and Huang 2009) was not explicitly corrected since most of it was absorbed by the random effects, as also concluded by Trincado G, Burkhart (2006). Another reason is that the autocorrelation, if any, cannot be supposed to be equal among observation sets and thus cannot be directly modeled.

2.3 Statistical methods

2.3.1 Mixed effect models maximum likelihood calibration

The taper model (2) was fit by maximum likelihood (ML) using the nlme library (Pinheiro et al. 2016) of R (3.2.1). The local calibration of a mixed effect model consists in estimating the random effect parameters for new individuals. According to Ni and Nigh (2012), there are two methods for estimating the random effect parameters and two for predicting the response variable, leading to four combinations, of which only two are coherent. In short, while the expected value of the random effect parameters is 0 by definition, the value used for calibration is more generally the estimation obtained at the latest iteration of the model fitting (iterative) process. Such estimation is itself based on a predictor, for instance the empirical best linear unbiased predictor (EBLUP). In this situation the construction of the prediction distribution is made based on the EBLUP expansion procedure, also known as the first-order conditional expectation (FOCE), initially proposed by Lindstrom and Bates (1990) and described and implemented by Huang et al. (2009). There are many examples of calibration following the method described by Huang et al. (2009), and it will not be described in further details here. The FOCE procedure followed to estimate the random expansion values here was based on Huang et al. (2009) and Ni and Nigh (2012). In this procedure, the EBLUPs were first estimated by iteration as presented in the R code associated to this article (Bouriaud et al. 2019), then applied to the new data.

2.3.2 Bayesian calibrations

The taper equation fit using the nlme package of R was subsequently used in a Bayesian Monte Carlo Markov Chain framework using Stan (Hoffman and Gelman 2011) with the library rstan (2.8.0, Stan Development Team 2016). Stan uses a Hamiltonian Monte Carlo algorithm, the No-U Turn Sampler. The default settings of the library were used for the runs presented in this study. It typically uses half of the prescribed number of iterations for the warmup, the posterior distributions being based on the successive iterations. Posterior estimates were based on post-warmup iterations only. The convergence was checked using the default functions of the rstan package using the Rhat statistics (Gelman and Hill 2007). Each post-warmup iteration provides a set of model parameters, predictions, and error estimations.

The first Bayesian calibration is based on the raw data of the fit dataset and is therefore referred to as a database Bayesian calibration (BCd). In the Bayesian framework, the taper equation was first fit to the fit dataset, which produced a first set of posterior distributions for the parameters. The equation was then fit to the application set. For this second fit, the priors of both the parameters and the variance components were taken from the posterior distribution of the fit realized on the fit data set. Both fittings are done simultaneously within each loop of the MCMC. The distribution of the parameters was supposed to be normal with means and variance to be determined based on the posterior distributions.

The second calibration method (BCl) is the one that would be used in the situation where the fit dataset cannot be used, and the prior relies on the fitted values of the parameters only. This situation is perhaps the most typical, when the parameters of the model and their error can be obtained from the literature but the (raw) data used for the fit are not. Several examples were reported in the field (see Zell et al. 2014). In our example, the parameters are obtained from the fit on the calibration sites, hence independently from the application zone, and only the fitted value of the parameters is being used as prior information for the calibration on the application site. This calibration is referred to as the literature-based Bayesian calibration (BCl) were prior information comes from independent studies and parameter distribution is often not reported in the published papers.

2.3.3 Volume estimations

The bole volume was estimated by numerical integration over 100 stem portions using the Smalian formula (see, e.g., Li and Weiskittel 2010 and references herein). For the MCMC estimations, the integration was repeated for each of the post-warmup iterations of the MCMC, thus providing an estimation of the standard deviation of the volume.

2.3.4 Fit statistics

The fit statistics included the mean bias of model predictions (bias), the root mean square error of prediction (RMSEP), estimated as:

$$ RMSEP=\sqrt{\frac{\sum_{i=1}^n{\left({Y}_{i,j}-{\hat{Y}}_{i,j}\right)}^2}{n}} $$

and

$$ {bias}_j=\frac{\sum_{j=1}^n{Y}_{i,j}-{\hat{Y}}_{i,j}}{n} $$

where n is the number of observations across all the trees and positions in a given dataset, Yi, j is the measured stem diameter for a given position i in a tree j, and \( {\hat{Y}}_{i,j} \) is the corresponding estimated stem diameter. Both RMSEP and bias are computed on the dataset used for the fit and on the evaluation dataset, as a measure of the prediction capacities of the model.

The effects of the calibration on the tree bole volume was also tested based on the RMSEP and bias using the same formulas, such that Yi, j is the measured volume (based on measured diameters) of tree i in batch j, while \( {\hat{Y}}_{i,j} \) is the corresponding estimated volume based on predicted diameters for each of the non-calibrated or calibrated models.

3 Results

3.1 Taper model fit

The fit dataset was constituted of 126 spruce trees measured from 16 different plots across Romania with diameter ranging from 5.6 to 66 cm and a mean slenderness (ratio of total height to diameter at 1.3 m) of 9.996 ± 2.571. The taper model (2) was fit with three random plot-level terms using maximum likelihood (Table 2). The model did not present signs of bias (Figs. 1 and 2) and fitted conveniently the stem profile of the trees despite the great variability of their provenience.

Table 2 Inference of the parameters using maximum likelihood (ML, left 4 columns) versus Bayesian model in Stan (fitted within MCMC using 2 chains each with 1000 post-warmup draws) for the taper model (3) fitted on the fit dataset
Full size table
Fig. 1
figure 1

Stem profile of all trees used for the taper model fit based on the ML fit of the model (3).The relative height is the ratio between the height at any point above the ground (h) to the top height of the tree (H). Similarly, the relative diameter is the ratio between the diameter at any point (d) to the breast-height diameter (dbh)

Full size image
Fig. 2
figure 2

Residuals of the model (3) fitted by maximum likelihood versus model predictions

Full size image

Based on the same input data, the model was fit in the Bayesian MCMC framework. The prior was the estimation of the ML fit, which was meant to maximize the similarity between the ML and the Bayesian fits, since the use of different start or prior values did not prove influential in our case (Fig. 3). The metropolis acceptance probability was high (0.87) and the Rhat values very close to 1 for all the model parameters. ML and Bayesian fit resulted in very similar parameter estimates. The discrepancy in the parameters estimation between the ML and Bayesian fit was less than 4% of the estimation on average but parameter stability was higher for the ML fit (low std error/parameter value) (Table 2). The slight differences in estimated parameters had little influence on the stem profiles fitted, which were very similar for both models, with a mean absolute difference of 0.01 (Fig. 3).

Fig. 3
figure 3

Comparison of the ML and Bayesian stem profile model fit. a Modeled diameter against relative height. b Comparison of the modeled diameters for the fit dataset

Full size image

3.2 Likelihood calibration

First, the ML estimations of the model (3) were used directly to estimate the stem profile of the trees of the application sets. The prediction errors without local calibration were important in the high-elevation dataset (Fig. 4, site 2 batch 2). The application set was subsequently split in two: one batch of 12 trees was used to estimate the random effects using the FOCE methods while the second batch of 12 trees (evaluation batch) was held for testing the model after calibration.

Fig. 4
figure 4

Residual graphs of the predicted relative diameter for each application site and evaluation batch. ML refers to the mixed-effect prediction not calibrated, ML FOCE to the FOCE calibration, BCd to the data-based Bayesian calibration, and BCl to the literature-based calibration. Within each site models are calibrated on one batch (the calibration batch) of 12 trees, then applied on the other batch (the evaluation batch) and residuals are expressed as measured-predicted

Full size image

The estimated random effects were globally smaller than the parameters themselves (Table 3) and represented 31–92% of the standard error of the parameter prediction. The calibration resulted in a mild reduction of the RMSEP (by 6.5 to 25.3% according to the test site, estimated as percent of the non-calibrated model’s RMSEP) and the bias (up to 97% reduction) but not in all situations (Fig. 4, Table 4) because some trees displayed a profile different from the others and had a strong influence on the validation statistics.

Table 3 Estimation of the random effects and model (3) parameters for each site and calibration batch. BCd refers to the Bayesian data-based calibration while BCl refers to the Bayesian literature-based calibration
Full size table
Table 4 RMSEP and mean bias decrease of the diameter model predictions as percent of the non-calibrated ML model. FOCE refers to the calibration based on estimating random effects using the first-order conditional expectation procedure, BCd refers to the Bayesian data-based calibration, and BCl refers to the Bayesian literature-based calibration
Full size table

3.3 Bayesian calibrations

The data-based calibration (BCd) was based on the posterior estimation of the model (2) fit parameters, which were used as priors for the fit of the same model to the new test data. The new parameter values for the test dataset differed substantially from the prior values (Table 3) from 1.3 to up to 10%. After calibration, the RMSEP on the fit batch generally decreased more strongly than using ML FOCE calibration: from 4 to 65% according to the site (Table 4) and the bias from 4 to 97%. On the evaluation set, the RMSEP on the decreased by 5–65% and the bias from 4 to 97% (Fig. 4). The small size-tree on site 2-batch 1 behaved differently from site 2-batch 2 and was responsible for the higher bias and smaller RMSEP decrease. However, the fit with BCd was globally much better than that of the ML.

Similarly, the literature-based Bayesian calibration BCl resulted in decreased RMSEP (4–65%) and bias (7–96%), and had values very comparable to that of the BCd (Fig. 4). Occasionally, the bias reduction was even stronger than in the BCd.

The distribution density of the diameter prediction errors (measured-predicted) showed that the absence of calibration resulted in larger errors and bias, which were strongly reduced by the local calibration (Fig. 5). The calibrated predictions (FOCE) represented a mean prediction error (over all the validation trees) of ~ 3.16 mm (against 3.34 mm for non-calibrated predictions) and a maximum error of ~ 22.94 mm from the non-calibrated predictions. But the Bayesian calibrations reduced even further the error magnitude with a mean error of 2.45 mm and 7% more diameters within the range of − 1 to + 1 mm from the measured value.

Fig. 5
figure 5

Distribution density of the prediction error of the diameter on both application sites according to the calibration method

Full size image

3.4 Consequences on the estimation of the stem volume

Stem volume is an integrated representation of the taper fit. In order to quantify the consequence of the deviations in the modeled stem profile, the bole volume resulting from the integration of the model were computed for each variants: ML without local calibration, ML with local calibration, BCd, and the BCl. The difference between local calibrated and uncalibrated predicted volumes ranged from − 5.2 to 3.3% (Fig. 6), thus representing a maximum deviation of ~ 0.1 m3 from the non-calibrated predictions at tree level. Globally, for the two test stands, local calibration resulted in larger predicted volumes (Table 5). The difference between BCd and BCl calibrations was smaller than the prediction’s confidence interval and can be deemed insignificant. Nevertheless, the calibration resulted in systematic and strong reductions of the bias of volume estimations, with the strongest reductions for the Bayesian calibrations (Table 5). The RMSEP was likewise noticeably reduced by the calibration with the exceptions of the FOCE calibration.

Fig. 6
figure 6

Distribution of the difference in estimated stem volume between the non-calibrated ML estimation and the calibrated estimations over both sites

Full size image
Table 5 Comparison of the batch-level descriptive statistics of the estimated tree volume, according to the calibration method. The mean volume and the RMSEP are expressed in liters
Full size table

4 Discussion

Calibrating the model improved markedly the predictions but high biases remained. The Bayesian calibrations proved superior to the ML one, particularly for their ability to reduce biases. The BCl proved as good as the more difficult calibration using raw data BCd.

These results confirm the fact that the Bayesian calibration improves substantially the prediction abilities of a model. Interestingly, the Bayesian calibration based on the sole knowledge of the parameters fit on external data (the literature-based calibration) proved as good as the more elaborate method—but difficult to implement—which requires the raw data. Hence, the literature-based calibration seems a very efficient and desirable option because it is very simple to implement and much faster. The new sampling algorithm implemented in Stan has brought a significant improvement compared to previous MCMC algorithms, which could be slow. But even so, the fit of the data-based Bayesian calibration takes several minutes of computation, compared to several seconds only for the literature-based calibration. Analyzing aboveground biomass equations for several species, Zell et al. (2014) came to the same conclusion that a Bayesian calibration performs very well even with reduced sample size, but has the advantage over other biomass estimation procedures to provide prediction intervals.

The ML calibration appeared to bring fewer improvements than the Bayesian calibration. The main reason for the discrepancy between the two families of method mostly comes from the fact that the ML calibration can only tune the parameters of the model that have a random component. In this study, three out of six parameters had a random component. Increasing the number of random parameters may not always be possible and convergence issues can rise. For one given model, the number of parameters that can be left as mixed-effect parameters may differ according the data as, e.g., in Meng and Huang (2009). The Bayesian calibration therefore has an appreciable advantage over the calibration of mixed-effect models that all parameters are being optimized together during the calibration procedure and has no computational issues, long as the Markov chain converges.

The model fitted used diameters measured at successive heights, up to the tree top. Contrarily to other studies where the model is localized using a single additional diameter (i.e., on top of the traditional dbh) taken at an upper stem position (e.g., Cao 2009), the model here was fitted based on more than 5 additional measurements per tree. Despite using more measurements, biases remained and the prediction errors without calibration remained important.

The number of trees used for the calibration may be influential. Here, we used a balanced split design where 12 trees were constantly used for both the calibration and the evaluation, and were sampled in the same diameter size class, to avoid extrapolation pitfalls. Our study proves that a reduced number of trees are sufficient to reduce substantially the prediction error and the bias of a model. Nevertheless, it should be noted that some trees displayed divergent profiles and created difficulties both in the fit and the validation. One way to cope with such trees may be to realize successive random draws from the same sample and use the average parameter value over the draws.

The estimated random effects were always smaller than the standard error of the parameters estimation, yet contributed greatly to improve the model fit. The gain in using random effects was perhaps maximized in this study, because the stands used for the calibration and validation were purposely sampled from sites displaying very different growing conditions. This situation is however representative of protected forests where tree form differs significantly from managed and open forests and where sampling is often prohibited. In our case, gain resulting from local calibration can be seen from the parameter values obtained for the two application sites: they were substantially lower (b) and higher (c and d) than the values obtained for the mean population of the fit dataset (Table 4) meaning that trees of these forest reserves have a lower taper (more cylindrical) and higher butt-swell at a fixed diameter and height. A direct application of the model, without local calibration would thus result in an underestimation of the true volume.

The consequences of a non-local calibration on the estimation of the volume were in the 5% range, which can be considered as low. But because of the bias, the errors would not compensate between trees and any stand-level application would result in a severe deviation of the per-hectare volume, in our case in the sense of a sub-estimation of the stand-level or per-hectare volume.

The methodology proposed in this paper is then of major importance for forests where sampling is difficult and even impossible (for instance in tropical rain forests). Given its parsimony, the local calibration can be performed from literature parameters and from very few felled trees (whenever possible), or from non-destructive measurements (see Picard et al. 2012), or from new technologies such as terrestrial LiDAR (Hackenberg et al. 2015). The literature-based calibration offers the possibility to reduce substantially such errors by defining an informative and constraining prior. The results can be generalized to other situations and other allometric models. The generality of the results comes from the fact that all the parameters of the allometric models can be tuned by the calibration simultaneously, and the calibration does not depend on a particular structure or model form. In our example, the model has twice as many parameters (6) as in classic volume or biomass allometric models that have only 2 or 3 parameters—plus potentially one more for the variance model in case of heteroscedasticity. This opens new possibilities to considerably improve national volume (and therefore biomass) estimations at national scales, especially for tropical countries where data availability can be very scares for both volume and biomass (Henry et al. 2011, 2013, 2015).

5 Conclusions

Several conclusions may be drawn from the study. First, the local calibration of the stem profile model reduced markedly the prediction errors: 4–65% reduction in the RMSEP for all calibration methods. The Bayesian calibrations performed better than the calibration based on estimating random effects with a stronger bias reduction (4–97% according to the tree). The Bayesian calibration based on literature data and a calibration dataset performed as well as the complex calibration based on both a fit dataset and a calibration dataset. The literature-based calibration thus represents a very promising method to locally calibrate allometric models with minimal measurements. However, regardless of the method, the local calibration of the taper model did not result in significant changes in the estimated stem volume with differences between non-calibrated and calibrated estimations ranging from − 5.2 to 3.3% of the non-calibrated volume.