Generalized Modified Inverse Weibull Distribution: Its Properties and Applications

Abstract

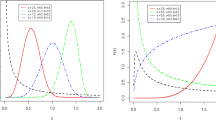
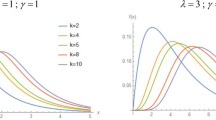
In this paper, we introduce a new useful continuous distribution called generalized modified inverse Weibull distribution. This distribution is a four-parameter extension of the modified inverse Weibull which generalizes some well-known distributions. Various statistical and probabilistic properties are derived such as r^th moment, moment generating function, Renyi and Shannon entropies and hazard rate function. We also discuss estimation of the parameters by maximum likelihood and provide the information matrix. The likelihood ratio order (which implies the hazard rate and usual stochastic orders) between smallest order statistics from two independent heterogeneous samples of this new family are discussed. Finally, a real numerical example is also considered for illustrative purposes.

Appendices

Appendix A: BesselK Function

$$\begin{array}{@{}rcl@{}} M_{T}(z)=E(e^{zT})={\int}_{0}^{\infty}\alpha \beta \left( \frac{1}{t}\right) (1-\exp(-\alpha/t))^{\beta-1}exp\{-\alpha/t) exp(zt) \} dt , \end{array} $$

by changing variable $(1-\exp (-\alpha /t))=x$, we have

$$\begin{array}{@{}rcl@{}} E(e^{zT})={{\int}_{0}^{1}}\beta x^{\beta -1} \exp\left\{ \frac{-z\alpha}{log(1-x)} \right\} dx , \end{array} $$

by changing variable 1 − x = y, we have

$$\begin{array}{@{}rcl@{}} E(e^{zT})&=&-{{\int}_{0}^{1}}\beta (1-y)^{\beta -1} \exp\left\{ \frac{-z\alpha}{log(y)} \right\} ,\\ &=& -\beta \sum\limits_{k = 0}^{\infty}\frac{{\Gamma}(\beta)}{{\Gamma}(\beta -k)}(-1)^{k}{{\int}_{0}^{1}}y^{k} \exp\left\{ \frac{-z\alpha}{log(y)} \right\}dy, \end{array} $$

where

$$\begin{array}{@{}rcl@{}} {{\int}_{0}^{1}}y^{k} \exp\left\{ \frac{-z\alpha}{log(y)} \right\}dy=\frac{2\sqrt{-\alpha z} BesselK(1,2\sqrt{(-\alpha z)(k + 1)})}{\sqrt{k + 1}}. \end{array} $$

Appendix B: Lagrange Inversion Formula

If F(x) is a series in x that satisfies the functional equation

Inverse of lagrange theorem (Stanley, 2011): If w is a power series with respect to x such that it is satisfies the following functional equation:

$$ F(x)=x \phi (F(x)). $$

Then g(F(x)) has laurent series with the following coefficient:

$$ [x^{n}]goF(x)=\frac{1}{n}[y^{n-1}] \left( g^{\prime}(y).\phi^{n}(y) \right). $$

Thus, we want to compute $\frac {1}{F(x)}$, i.e., $g(x)=\frac {1}{x}$ and F(x) = xexp(−F(x)). Therfore ϕ(x) = e^−x. Then $[x^{n}] \frac {1}{F(x)}=\frac {1}{n}[y^{n-1}][\frac {-1}{y^{2}}e^{-ny}]$. But

$$ \frac{-1}{y^{2}}e^{-ny}=\frac{-1}{y^{2}} \sum\limits_{i = 0}^{\infty}\frac{(-ny)^{i}}{i!}=\sum\limits_{i = 0}^{\infty}\frac{(-1)^{i + 1} n^{i} y^{i-2}}{i!}. $$

(10.1)

The coefficient of y^n− 1 in (10.1) is i − 2 = n − 1, i.e., i = n + 1 and finally

$$ [x^{n}]\frac{1}{F(x)}=\frac{1}{n}\frac{(-1)^{n + 2}n^{n + 1}}{(n + 1)!}=\frac{(-1)^{n} n^{n}}{(n + 1)!}. $$

Appendix C: Differential

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \alpha^{2}}&=&-\frac{n-m}{\alpha^{2}} +\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\alpha\alpha}\nu_{i}-\{(\dot{\nu}_{i})_{\alpha}\}^{2}}{{\nu_{i}^{2}}}\\&&-(\beta -1)\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\alpha\alpha}(1-\nu_{i})-\{(\dot{\nu}_{i})_{\alpha}\}^{2}}{(1-\nu_{i})^{2}} \\ &&-\beta\sum\limits_{i=n-m}^{n}\frac{(\ddot{\nu}_{i})_{\alpha\alpha}(1-\nu_{i})-\{(\dot{\nu}_{i})_{\alpha}\}^{2}}{(1-\nu_{i})^{2}}, \\ \frac{\partial^{2}\ell}{\partial \alpha \partial \beta}&=&-\left( \sum\limits_{i = 1}^{n-m}\frac{(\dot{\nu_{i}})_{\alpha}}{1-\nu_{i}}+ \sum\limits_{i=n-m + 1}^{n}\frac{(\dot{\nu_{i}})_{\alpha}}{1-\nu_{i}} \right), \end{array} $$

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \alpha \partial \gamma}&=& \sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\alpha\gamma}\nu_{i} - (\dot{\nu_{i}})_{\alpha}(\dot{\nu_{i}})_{\gamma}}{{\nu_{i}^{2}}}-(\beta -1)\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\alpha\gamma}(1-\nu_{i}) +(\dot{\nu_{i}})_{\alpha}(\dot{\nu_{i}})_{\gamma}}{(1-\nu_{i})^{2}} \\ &&-\beta \sum\limits_{i=n-m + 1}^{n}\frac{(\ddot{\nu}_{i})_{\alpha\gamma}(1-\nu_{i}) +(\dot{\nu_{i}})_{\alpha}(\dot{\nu_{i}})_{\gamma}}{(1-\nu_{i})^{2}}, \\ \frac{\partial^{2}\ell}{\partial \alpha \partial \lambda}\!&=&\!\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\alpha \lambda}\nu_{i} - (\dot{\nu_{i}})_{\alpha}(\dot{\nu_{i}})_{\lambda}}{\nu_{i}^{2}}-(\beta -1)\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\alpha \lambda}(1-\nu_{i}) +(\dot{\nu_{i}})_{\alpha}(\dot{\nu_{i}})_{\lambda}}{(1-\nu_{i})^{2}} \\ &&-\beta \sum\limits_{i=n-m + 1}^{n}\frac{(\ddot{\nu}_{i})_{\alpha\lambda}(1-\nu_{i}) +(\dot{\nu_{i}})_{\alpha}(\dot{\nu_{i}})_{\lambda}}{(1-\nu_{i})^{2}}, \end{array} $$

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \beta^{2}}&=&-\frac{n-m}{\beta^{2}} \end{array} $$

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \beta \partial \gamma}&=& \sum\limits_{i = 1}^{n}\frac{(\dot{\nu_{i}})_{\gamma}}{1-\nu_{i}} \end{array} $$

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \beta \partial \lambda}&=& \sum\limits_{i = 1}^{n}\frac{(\dot{\nu_{i}})_{\lambda}}{1-\nu_{i}} \end{array} $$

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \gamma^{2}}&=&-\sum\limits_{i = 1}^{n-m}(\gamma +\lambda /t_{i} )^{-2}+ \sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\gamma \gamma}\nu_{i}+ \{(\dot{\nu_{i}})_{\gamma}\}^{2} }{{\nu_{i}^{2}}} \\ &&-(\beta-1)\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\gamma\gamma}(1-\nu_{i}) + \{(\dot{\nu_{i}})_{\gamma}\}^{2}}{(1-\nu_{i})^{2}} \\ &&-\beta\sum\limits_{i=n-m + 1}^{n}\frac{(\ddot{\nu}_{i})_{\gamma\gamma}(1-\nu_{i}) + \{(\dot{\nu_{i}})_{\gamma}\}^{2}}{(1-\nu_{i})^{2}}, \end{array} $$

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\ell}{\partial \gamma \partial \lambda}&=&-\sum\limits_{i = 1}^{n-m}t_{i}^{-1}(\gamma +\lambda /t_{i})^{-2}+ \sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\lambda \gamma}\nu_{i}+ (\dot{\nu_{i}})_{\lambda}(\dot{\nu_{i}})_{\gamma}}{{\nu_{i}^{2}}} \\ &&-(\beta-1)\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\lambda\gamma}(1-\nu_{i}) +(\dot{\nu_{i}})_{\gamma} (\dot{\nu_{i}})_{\lambda}}{(1-\nu_{i})^{2}} \\ &&-\beta\sum\limits_{i=n-m + 1}^{n}\frac{(\ddot{\nu}_{i})_{\lambda\gamma}(1-\nu_{i}) +(\dot{\nu_{i}})_{\gamma} (\dot{\nu_{i}})_{\lambda}}{(1-\nu_{i})^{2}}, \\ \frac{\partial^{2}\ell}{\partial \lambda^{2}}&=&-\sum\limits_{i = 1}^{n-m}(\gamma t_{i} +\lambda )^{-2}+ \sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\lambda \lambda}\nu_{i}+ \{(\dot{\nu_{i}})_{\lambda}\}^{2} }{{\nu_{i}^{2}}} \\ &&-(\beta-1)\sum\limits_{i = 1}^{n-m}\frac{(\ddot{\nu}_{i})_{\lambda\lambda}(1-\nu_{i}) + \{(\dot{\nu_{i}})_{\lambda}\}^{2}}{(1-\nu_{i})^{2}} \\ &&-\beta\sum\limits_{i=n-m + 1}^{n}\frac{(\ddot{\nu}_{i})_{\lambda\lambda}(1-\nu_{i}) + \{(\dot{\nu_{i}})_{\lambda}\}^{2}}{(1-\nu_{i})^{2}}, \end{array} $$

where

$$\begin{array}{@{}rcl@{}} &&(\ddot{\nu}_{i})_{\alpha \alpha}=-(\dot{\nu_{i}})_{\alpha}t_{i}^{-\gamma}exp(\lambda/t_{i}),~(\ddot{\nu}_{i})_{\gamma \gamma}=-(\dot{\nu_{i}})_{\gamma}log(t_{i})(1+log(\nu_{i}),\\ &&(\ddot{\nu}_{i})_{\lambda\lambda}=(\dot{\nu_{i}})_{\lambda}\left( 1/t_{i}+(\dot{\nu_{i}})_{\lambda}/\nu_{i} \right),~(\ddot{\nu}_{i})_{\alpha\gamma}=-(\dot{\nu_{i}})_{\alpha}log(t_{i})(1+\alpha (\dot{\nu_{i}})_{\alpha} / \nu_{i}), \\ &&(\ddot{\nu}_{i})_{\alpha\lambda}=(\dot{\nu_{i}})_{\alpha}(1+\alpha (\dot{\nu_{i}})_{\alpha} / \nu_{i}) /t_{i},~ (\ddot{\nu}_{i})_{\gamma\lambda}=(\dot{\nu_{i}})_{\gamma}(1+log(\nu_{i})) /t_{i}. \end{array} $$