1 Introduction

Water is usually essential for human survival as well as the survival of almost all ecosystems [1]. Water contamination caused by technological advancement is still a major concern. Dyes are chemical substances that may connect to surfaces or textiles and produce color. Dyes and pigments are widely used in textiles, plastics, food, paper, leather, colorants in the cosmetic sector, and natural and synthetic fibers [2]. Several industries have been identified as the source of the increasing emission of colored effluents containing synthetic organic dyes [3]. Methyl orange (MO) is one of the most commonly dye used in the textile industry [4, 5]. It is also used as a pH indicator for titrations [6,7,8]. The release of colored wastewater into the environment has negative impacts on the receiving water bodies and poses significant risks since they contaminate natural habitats and are not biodegradable [9]

Aquatic organisms have also been shown to be mutagenic and carcinogenic to synthetic dyes as well as human life, causing major heart, kidney, liver, reproductive, and nervous system malfunctions. Because of their obstinacy, their emissions into the hydrosphere contribute significantly to pollution. This will give the water reducing sunlight penetration, an unattractive color [10].

Over 10,000 tonnes of dye are used worldwide in the textile industry each year, with approximately 100 tonnes of dye discharged into waterways each year [11, 12]. Fundamentally, the exact amount of dyes discharged into the environment from different procedures is unknown. However, environmental scientists have serious worries about the leakage of significant volumes of synthetic dyes into the environment. Some of the procedures used to remove colors from wastewater include membrane separation [13], coagulation, adsorption, and advanced oxidation [14, 15]. However, the preivous menthioned methodology have several disadvantages like the complexity, high operational cost and time-consuming unit operations as stated above [16].

Adsorption is a very successful advanced wastewater treatment process used to diminish dangerous inorganic/organic contaminants in effluent [17, 18]. The goal of the present work is to identify a low-cost alternative to blue-green algae as an adsorbent. Numerous studies have been done to determine whether natural resources, biosorbents, industrial solid wastes, and agricultural byproducts can be used as precursors for different low-cost adsorbents. The study also said that raw biomass adsorbents were subjected to various chemical or physical treatments in order to improve their adsorption ability [19].

Green nanotechnology is a method of nanomaterials production that is free of harmful components or uses less hazardous components throughout the manufacturing process [20]. Biological elements like actinomycetes, bacteria, cyanobacteria, fungi, macroalgae, and plants can all be employed to green synthesize NPs. Green synthesis is chosen over chemical and physical methods because of its affordability, environmental friendliness, scale, simplicity, and biocompatibility [21, 22]. Blue-green algae Arthrospira platensis is a widely grown species with a high yield of 2000 tonnes per year [23]. Arthrospira platensis, a filamentous cyanobacterium with various advantages such as high biomass output, fast growth rates, biomass composition adjustment, and simplicity of cell harvesting, is a possible biosorbent. Arthrospira platensis is a well-known source of polysaccharides, protein, minerals, lipids, phosphate, and vitamins [24], they are all essential for dye-binding [25].

Using a batch method, the effects of numerous parameters such as initial MO concentration, contact time, pH, temperature, and adsorbent dose on the adsorption rate and processes of MO onto A. platensis were examined. In addition, Brunauer–Emmett–Teller (BET), Fourier transform infrared (FT-IR), and scanning electron microscopy (SEM) were used to assess the adsorbent's morphology and physicochemical characteristics. Subsequently, we further analyzed the adsorption capacities and efficiencies, and data of equilibrium used to determine adsorption isotherms, kinetics, and thermodynamics in order to assess the adsorption mechanism and rate constants. This study provides valuable insights for further exploring the potential of blue-green algae, A. platensis, frameworks in dye adsorption applications especially in case of ease of regeneration, cost effective, stability, and quick synthesis. This study has the potential to provide deeper understanding of MO adsorption, thereby enhancing the knowledge base for future work. Additionally, it can minimize the subjective selection of adsorbents for MO adsorption, resulting in a decrease in the volume of published literature that adds little or only marginal value to the field.

2 Materials and methods

2.1 Chemical reagents

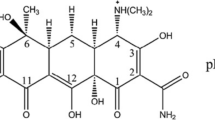
Alpha Chemika in India provided methyl orange (2-(N, N-dimethyl-4-aminophenyl) azo benzene carboxylic acid), which was utilized as a commercial dye. Through diazotization of anthranilic acid, methyl orange had been equipped, after which a reaction with dimethyl aniline occurs. Table 1 shows the chemical formula, molar mass, melting point, kinds of dyes, density, extreme adsorption wavelengths, and molecular structure. To avoid direct light exposure, the equipped stock was kept in the dark. However, 1 g of the dye powder was dissolved in 1 L of distilled water (DW) to make a stock solution. Each adsorption experiment solution was prepared by diluting the stock to the required concentration. The pH of the solution was adjusted using either 1 M HCl or 1 M NaOH.

Table 1 Properties of methyl orange dye
Full size table

2.2 Adsorbent preparation

The preparation of A. platensis nanoparticle was caryed out at the Egyptian Petroleum Research Institute (EPRI), Nasr City, Cairo, Egypt, via ball grinding (Planetary Ball Mill PM 400 “4 grinding stations”), as detailed in our previous publication [26]. As demonstrated in our earlier works [26,27,28], the size distribution of A. platensis nanoparticles was determined using dynamic light scattering (DLS), resulting in average sizes of 183.9 nm (87.6%) and 1069 nm (12.4%). In contrast, the typical size of the A. platensis alga was 100 µm [26,27,28].

2.3 Batch adsorption experiments

Experimentations for MO removal were accompanied in an air-tight Erlenmeyer flask (500 mL) by captivating 200 mL of 50 mg L−1 dye solution. The temperature of the system was saved constant at 25 ± 2 °C. Samples were withdrawn and filtered during contact times to isolate the adsorbent from the dye solution. Spectrometric analysis was used to assess the concentration of the dye solution, all experimentations were accomplished. Experiments were carried out to explore the effects of initial dye concentration on dye absorption, with dye concentrations ranging from 5 to 50 mg L−1 at constant dosages of 0.1 g at pH 7 [24, 29].

By changing the initial pH of the dye from 1 to 11, the effects of the final pH on MO adsorption were investigated. Prior to measuring the final pH, the adsorbent and the dye mixture were permitted to equilibrate for 120 min in a shaker at 25 ± 2 °C to the final pH measurement. While the effects of contact time at a range from 10 to 120 min and adsorbent doses (0.05 to 0.4 g) were studied at a constant initial dye concentration of 5 mg L−1 at a constant temperature of 25 ± 2 °C and pH 7. Samples were shaken in a temperature-controlled incubator shaker at 25 °C and 180 rpm. At a predetermined period ranging from 5 to 120 min, samples were withdrawn for spectrophotometric analysis [29, 30].

2.4 Equilibrium studies

To assess the type of adsorption isotherms and the sorption capacity of the adsorbent for MO dye removal, adsorption equilibrium analyses were performed. The processes of adsorption were examined using pseudo-first-order and pseudo-second-order models, as well as an intra-particle diffusion mechanism. The kinetic characteristics were examined for contact times between 10 and 120 min. The parameters of adsorption isotherm models were also considered to know adsorption behavior. The initial dye concentrations for the isotherm studies were varied from 5 to 50 mg l−1 using 0.1 g of biomass of adsorbent. Besides, the thermodynamic investigations were carried out in an incubator shaker for 2 h at different temperatures ranging from 25 to 65 °C in an incubator shaker for 2 h. At the end of the experiments, the samples were filtered, and the residual concentration was calculated. The % elimination of the dye was estimated using the reduction in absorbance at the dye’s maximum value as follows [16]:

$${\mathrm{q}}_{\mathrm{e}} (\mathrm{mg }{\mathrm{g}}^{-1}) = [({\mathrm{C}}_{\mathrm{i}}- {\mathrm{C}}_{\mathrm{f}}) \times \mathrm{ V}] /\mathrm{ W}$$
(1)
$$\mathrm{Percentage removal }(\mathrm{\%}) = [({\mathrm{C}}_{\mathrm{i}}- {\mathrm{C}}_{\mathrm{f}}) / {\mathrm{C}}_{\mathrm{i}} ] \times 100$$
(2)

where: Ci and Cf (mg L−1) are the initial and final MO concentrations at a given time, respectively; V is the dye mixture volume (L), and W is the dry adsorbent weight (g).

2.5 Characterization of adsorbent material

2.5.1 Fourier transform infrared (FTIR) spectroscopy

FTIR spectroscopy was used to analyze the chemical structure by VERTEX 70 FT-IR-Bruker spectrometer. The substance was mixed with 1% KBr and crushed into pellets before being studied in the mid-infrared range (500–4000 cm−1) at 4 cm−1 resolution [31].

2.5.2 Scanning electron microscopy (SEM)

Under a 30 kV accelerating voltage, the samples’ surface morphology was examined using a scanning electron microscope (SEM, FEI, Quanta 200, Thermo Scientific, Waltham, MA, USA). SEM was used to verify the morphological variations between the nanoparticles of A. platensis biomass before and after MO dye sorption.

2.5.3 BET investigation

The specific surface area and pore volumes of the adsorbent were measured to assess whether the porosity of the sample under consideration had changed. The nitrogen adsorption–desorption isotherms of impregnated nanoparticles A. platensis at 77.33 K. The textural properties of nano A. platensis were obtained using the instrument (NLDFT Ads. model) analytical software and certain parameters were obtained using BET, t-plot, and BJH-Des techniques.

2.6 Equilibrium isotherm

2.6.1 Langmuir and Freundlich models

The Langmuir model, which is based on the notion that intermolecular interactions drop rapidly with distance and may thus predict the presence of monolayer coverage for the sorbate on the sorbent’s exterior surface, was carefully chosen.

While the Freundlich model is used to demonstrate system heterogeneity and define the reversible sorption process, it does not reveal whether dye ion retention happens in several layers. The linear forms described below were used to compute the mathematical formulas of the Langmuir model (see (3)) and the Freundlich model (see (5)) [32] and [33]:

$$\frac{1}{{{\varvec{Q}}}_{{\varvec{e}}}}=\boldsymbol{ }\frac{1}{\mathbf{b}{{\varvec{q}}}_{{\varvec{m}}{\varvec{a}}{\varvec{x}}}}\times \frac{1}{{{\varvec{C}}}_{{\varvec{e}}}}+\frac{1}{{{\varvec{q}}}_{{\varvec{m}}{\varvec{a}}{\varvec{x}}}}$$
(3)
$${q}_{e}={K}_{f}{C}_{e}^{1/n}$$
(4)
$$\mathrm{Log}{q}_{e }={\mathrm{Log}K}_{f }+\frac{1}{n} \mathrm{Log}{C}_{e}$$
(5)

where: qe denotes the equilibrium adsorption capacity, qmax means the maximum sorption capacity and b represents the Langmuir constant. While, Kf indicates the Freundlich constant, and n represents the heterogeneity factor.

2.6.2 Temkin isotherm model

As indicated by the following linear equation, the Temkin equation posits that the heat of the sorption process reduces linearly with adsorption coverage due to adsorbent-adsorbate interactions [34]:

$${q}_{e}= B \mathrm{ln} A + B \mathrm{ln}{C}_{e}$$
(6)

where: B = (RT b−1) (J mol−1) is the Temkin constant and related to the heat of adsorption, T denotes the absolute temperature (K), R (8.314 J mol−1 K) means the ideal gas constant, and A refers to the value for the higher binding energy’s associated equilibrium binding constant (L min−1).

2.6.3 Dubinin-Radushkevich (D-R) isotherm

Dubinin-Radushkevich’s (D-R) isotherm model was used to assess whether the sorption method was chemical or physical [35]. The Dubinin-Radushkevich model is frequently used in the following equation:

$$\mathrm{Ln }{\mathrm{q}}_{\mathrm{e}} =\mathrm{ Ln }{\mathrm{q}}_{\mathrm{m}}-\mathrm{K }{\varepsilon }^{2}$$
(7)
$$\varepsilon =\mathrm{ RT Ln }(1 + 1/{\mathrm{C}}_{\mathrm{e}})$$
(8)
$$E = 1 /\sqrt{(2K)}$$
(9)

where: The polanyi potential and the adsorption capacity constant, qm (mg g−1), are both present. The adsorption means free energy constant is K (mol2 kJ−2), the sorption energy constant is E (kJ mol−1), the gas constant is R (J mol−1 K−1), and the absolute temperature is T (K).

3 Results and discussion

3.1 Adsorbents characterization

3.1.1 FTIR spectrum

The kind and quantity of functional groups on the adsorbent’s surface significantly affect MO adsorption [36]. Figure 1 depicts the results of the identification of the functional groups of the adsorbent using an FTIR spectrometer. The broadband at the range of 3421 to 3364 cm–1 can be attributable to bond –OH and –NH groups. The peak at 2924 cm–1 indicated the aliphatic C–H groups. The peak at 2855 cm–1 after remediation is caused by asymmetric CH3 stretching and both asymmetric and symmetric CH2 stretching [37], which are commonly observed in microalgal biomass. The band at 2076 cm−1 represents C≡C groups. While the C = O group may be responsible for the peaks around 1637 and 1650 cm–1 before and after remediation. The band created after adsorption at 1545 cm−1 can be assigned to C = C stretch aromatic or N–H bending types of bonds of amide (II). To aromatic rings, this group can be conjugated or unconjugated [38, 39]. While, the absorption band at 1419 cm−1 split into two peaks at 1451, and 1431 cm−1 indicating the presence of sp3 C-H bend. The peak at 1361 cm–1 identified the aliphatic C–H groups. In the A. platensis nanoparticles alga, a deformation related to the C–O bond was observed around 1100–1350 cm−1. Moreover, before and after adsorption, stretching vibrations –C–O was discovered at adsorption peaks at 1048 and 1033 cm–1 [40]. The adsorption bands in the 750–900 cm─1 range are caused by S–O, P-O, and aromatic C-H stretching vibrations [41]. The broadening and shifting of peaks on spectra suggested the interaction of functional groups on the outer layer of the A. platensis cell wall with MO dye ions in an aqueous solution. According to the FTIR spectrum of the adsorbent, MO ions may bind to anionic groups and amino groups by electrostatic attraction. The NH2, C = O and OH groups, in addition to the aromatic groups present in the bio-mass, and the sulfate and phosphate peaks regions, were detected when the adsorbent was loaded with MO.

Fig. 1
figure 1

FTIR spectra: A before adsorption; B after adsorption of MO dye

Full size image

3.1.2 Scanning electronic microscopy (SEM)

The form, size, and surface features such as morphology were investigated using SEM. A. platensis nanoparticles’ surface shape before and after MO adsorption was depicted in Fig. 2a and b. The SEM morphology of nanoparticles A. platensis was found to be irregularly dispersed and spherical. This showed that the surfaces of microalgal cells were heterogeneous. The active sites were homogeneous before adsorption, which led to the creation of spherical particles with a uniform distribution, according to SEM examination. And the outer layer of cells was found to be uneven, porous, with aggregation, irregularity, and small particles covering it after MO adsorption. The SEM image of the cells following sorption also reveals that amorphous materials gathered all over the cell surface. It was possible to see pores and tubes of different sizes and forms. It is believed that the small particles contain released cell contents from the therapy. According to Adeyi, et al. [42], the MO cations created a MO ion monolayer on the surface of the A. platensis nanoparticles by covering the adsorbent particles and filling in the gaps.

Fig. 2
figure 2

SEM of A. platensis nanoparticles before (A) and after (B) adsorption process of MO dye

Full size image

3.1.3 BET examination

The application of the adsorption method is most strongly influenced by the physical characteristics of the adsorbent as assessed by BET analysis. The specific surface area of A. platensis nanoparticles was examined using the N2 sorption isotherms at 77 K. Figure 3 displays the nitrogen adsorption/desorption isotherms. The surface area of the A. platensis nanoparticles measured by multipoint BET and single point BET, respectively, was 139.83 m2 g−1 and 114.373 m2 g−1. For the synthetic adsorbent, this is a reasonable value. It is important to note that MO dye is absorbed from an aqueous solution more effectively the larger the surface area. The BJH adsorption cumulative micropore volume was 0.101 cc g─1. While the BJH adsorption pore radius was 1.55779 nm, however, the BJH desorption pore radius was 1.63 nm. Since algal swelling in aqueous solutions increases the surface area of A. platensis nanoparticles, the results demonstrate the particles had a significant surface area.

Fig. 3
figure 3

BET analysis for A. platensis NPs, BJH-adsorption-dS(r) (A), BJH-desorption-dV(r) (B), DFT method-pore volume (C), and DFT method histogram- volume (D)

Full size image

3.2 Factors influencing batch adsorption

3.2.1 Influence of contact time and initial MO concentration

The initial concentration effect (5, 10, 20, 30 mgL−1) on MO adsorption onto 0.1 g of A. platensis at various times (5, 10, 15, 30, 60, 120, and 180 min) and a constant rate of 150 min was studied. The findings are examined, and the results are summarized in Fig. 4. An increase in the adsorption process was observed from 3.7 to 17 mg g−1 for raw biomass with a 5 mgL−1 initial concentration of MO. Figure 4 shows that for MO concentrations of 5, 10, 20, and 30 mg L−1, the removal % was 70, 25.4, 52.3, and 51.6, respectively, for the initial MO concentration of 0.1 g at 180 min. This findings demonstrated that the sorption capacity increases when the concentration of the initial MO dye increases. This suggests that the initial dye concentration has an impact on dye sorption. Ion exchange or physical adsorption at the cell surface may be involved in the initial rapid phase, while other mechanisms such as binding site saturation, micro-precipitation, or complexation may be included in the subsequent slower phase. It is possible that this is a result of the driving force to break through all dye molecule mass transfer barriers among the solid and aqueous phases [43].

Fig. 4
figure 4

Influence of contact time and different initial MO dye concentrations on A. platensis NPs adsorbent (constant dosages of 0.1 g at a constant temperature of 25 ± 2 °C at pH 7 and 180 rpm)

Full size image

The initial concentration of MO dye ions (which could conflict with the ions of interest for active sorption sites) also influences the adsorption rate [44]. At the initial stage, the adsorbent’s surface is bare; sorption occurs rapidly and is normally controlled by a diffusion process from the bulk to the surface. Adsorption is likely an attachment-controlled process at this stage since there are fewer potential sorption sites [44].

The equilibration time necessary for sorption was found to be around 30 min for all initial MO dye concentrations because the equilibrium reaching time was independent of dye concentration, demonstrating that rapid adsorption happened and that sorption was not governed by film diffusion from bulk to surface [43]. The typical route taken by the dye molecules from the bulk solution to the exterior surface of the adsorbent via the liquid film, and then from the exterior surface of the adsorbent to the pores, demonstrates that the initial concentration of dye is significantly increased by the dye adsorption onto the adsorbent [43]. For a given adsorbent dose, the total number of potential adsorption sites is typically fixed. It is reasonable to assume that at lower initial concentrations, the adsorbent has a larger ratio of active adsorption sites. As a result, at lower initial concentrations, the percentage of dye removed is greater, whereas at higher initial concentrations, it is lower.

3.2.2 Effect of adsorbent dosage

The influence of adsorbent dose provides a clue as to a dye’s ability to sorb with the least quantity of adsorbent possible, enabling the economical recognition of a dye’s potential. The adsorbent dose is also a significant restriction on dye adsorption, which was also studied for biomass dosage in values 0.05, 0.1, 0.2, 0.3, and 0.4 g 50 mL−1 range while other factors remain unchanged. Figure 5 summarizes the effect of adsorbent dosage. The MO amount eliminated is greatly dependent on the adsorbent dose. The maximum dye adsorption of 40.7, 46.1, 47.1, 47.2, and 47.7 (mg g−1) in biomass dosages of 0.05, 0.1, 0.2, 0.3, and 0.4 g, respectively. Besides, the percentage of dye removal increases with increasing biomass dosage from 0.05 to 0.4 g with percentage (92.6 to 95.6%). By a fixed initial dye concentration, an increase in increase in the adsorbent surface area and availability of more adsorbent sites resulted in an increase in percentage removal % and MO adsorption capacity [45, 46]. Furthermore, this is most likely due to dye mass transfer resistance from bulk liquid to a solid surface, which becomes significant at great adsorbent loading, as was shown in the experiment [47, 48].

Fig. 5
figure 5

Impact of different initial doses (g) of A. platensis NPs on MO dye removal (%) (at a constant initial dye concentration of 5 mg L.−1, constant temperature of 25 ± 2 °C at pH 7 and 180 rpm for 120 min)

Full size image

Nevertheless, increasing the adsorbent dosage leads to little improvement in the adsorbent. This could be because adsorbent particles collide more frequently, as a result, there are fewer unoccupied sites available for adsorption per unit mass of adsorbent, and such collisions may result in active site aggregation or overlapping. As a result, 0.04 g was selected as the optimized adsorbent dose and was used for the rest of the experiment [49]. In general, when the amount of sorption sites rises at the surface of the adsorbent with increasing adsorbent dose, therefore, the dye removal increases [50].

3.2.3 Influence of solution pH

The sorption process depends on the dye solution’s pH, particularly its adsorption capacity. As shown in Fig. 6, the effect of different solution pH (1–11) on the equilibrium uptake of MO dye was studied at constant levels of other variables. The dye uptake was shown to decrease as the pH increased. Various species adsorbed on different adsorbents will have varied pH ranges for adsorption. When 87.52% of the MO was removed, the adsorbent’s maximum adsorption capacity was 25.719 mg g−1 at pH 1 at an initial dye concentration of 5 mgL−1 at 25 °C. The amount of dye removal decreased by 39% in the pH range of 1 to 7. Founded on current data, the initial pH of all adsorbate solutions was kept at 1. While, the adsorbent’s major sorption capacity for MO adsorption occurs around pH 1.0–3.0 because the amino groups are protonated at this pH range, facilitating the adsorption of the negatively charged dye [51]. This also suggested that the electronic interaction between adsorbent and adsorbate was not the dominant factor. Furthermore, the dimer form may be more difficult to permeate through the micropores of the adsorbent particle than the smaller monomeric MO [49].

Fig. 6
figure 6

Effect of different pH values of A. platensis NPs on MO dye removal (at a constant initial dye concentration of 5 mg L.−1 for 120 min, with constant temperature of 25 ± 2 °C at Constant dosages of 0.1 g and 180 rpm)

Full size image

3.2.4 Influence of temperature

At an initial concentration of 5 mg l−1, the impact of temperature on the equilibrium alga sorption capacity for MO was examined over the temperature range of 20–60 °C. As presented in Fig. 7, the equilibrium uptake of MO reduced with boosting temperature demonstrating that sorption between adsorbent and MO was an exothermic process with physical adsorption being the main mechanism at lower temperatures. At 20 °C, the maximum equilibrium absorption of MO was 99.83%, with an equilibrium sorption capacity of 49.78 mg g−1. Adsorption of MO was likewise oppositely proportional to temperature increase, i.e. increasing temperature until 60 °C resulted in a reduction in equilibrium uptakes from 98.73% (20 °C) to 96.78% (60 °C) due to decreased surface activity. Also, a reduction in temperature increases adsorption, a phenomenon that is observed in physical adsorption [52].

Fig. 7
figure 7

Influence of temperatures (°C) of A. platensis NPs on MO dye removal (at a constant initial dye concentration of 5 mg L.−1 for 120 min, with constant dosages of 0.1 g and 180 rpm)

Full size image

3.3 Thermodynamic study

In to decide which process will occur spontaneously, every adsorption process needs to take into account entropy factors. The actual indicators for a process’s practical applicability are the values of thermodynamic parameters. The amount of MO adsorbed onto the adsorbent at equilibrium at various temperatures (20–60 °C) was examined (Table 2) in order to determine thermodynamic parameters for the adsorption system. The thermodynamic parameters such as enthalpy (ΔHo), a change in the standard free energy (ΔGo), and entropy (ΔSo) were calculated by applying the following equations:

Table 2 Thermodynamic manners of adsorption of MO onto A. platensis nanoparticles
Full size table
$${\mathrm{K}}_{\mathrm{d}} = {\mathrm{q}}_{\mathrm{e}}/{\mathrm{C}}_{\mathrm{e}}$$
(10)
$$\mathrm{\Delta G }= -\mathrm{ RT Ln }{\mathrm{K}}_{\mathrm{d}}$$
(11)
$$\mathrm{\Delta G}^\circ =\mathrm{\Delta H}^\circ -\mathrm{T \Delta S}^\circ$$
(12)
$$\mathrm{\Delta G}^\circ =\mathrm{ T }(\mathrm{\Delta S}^\circ ) +\mathrm{ \Delta H}^\circ$$
(13)

The value uses of enthalpy and entropy was calculated from the intercept and slope of the plotted curve of temperature vs. change in the standard free energy of Eq. (11) or (12), as well as ∆G°, which can be calculated from Eq. (13). The values of thermodynamic factors for the adsorption process are presented in Table 2.

The estimated negative value of (ΔH° =  − 70.88 kJ mol−1) showed that the adsorption process was exothermic; however, the positive values of entropy change (ΔS° = 0.1933 J mol−1 K−1) confirmed the high preference for MO molecules on the adsorbent surface [53]. The low negative enthalpy change values indicate exothermic and physical adsorption [54]. The values of ∆G° decreased from − 6.95 to − 4.63 kJ mol−1 for the Langmuir isotherm and ascended from − 13.99 to − 7.52 kJ mol−1 as the temperature increased from 20 to 60 °C. The minus sign of the change in free energy (∆G°) confirms the feasibility of adsorption processes and also reveals spontaneous adsorption of MO onto adsorbent in the temperature range studied. The average ∆G° value for the MO adsorption developed in this work is − 10.1 kJ mol−1, indicating that the dominating mechanism was physical adsorption via a physical process involving weak attraction forces. At the same time, the low value of ΔHo suggests that the adsorbate molecules were loosely bound to the adsorbent surface [55].

3.4 Adsorption isotherms

An adsorption isotherm describes the relationship between the concentration of adsorbate still present in the solution and the amount of adsorbate absorbed by the adsorbent. These equilibrium models’ equation variables often show the adsorbent’s affinity, surface properties, and adsorption mechanism. In this analysis, four significant isotherm models were chosen to account for the experimental equilibrium results.

3.4.1 Langmuir

According to the Langmuir equation, an adsorbed solute monolayer will form [56]. The monomolecular sorption capacity (qm), comparable to full monolayer coverage on the biomass surface, was calculated using the Langmuir adsorption isotherm. Table 3 shows the values of qm, b, and the coefficient, R2. The outcomes show that the Langmuir equation is followed during the sorption of MO dye ions onto an adsorbent, as seen through the high correlation values R2 = 0.999 as presented in Fig. 8. The monomolecular adsorption capacity qmax showed that the adsorbent (156.25 mg g−1) has a higher mass capacity. The separation factor was used to investigate the interaction of dye ions with adsorbents further (RL). The equilibrium parameter RL of the Langmuir model is a dimensionless constant separation factor. The RL was defined by Hall et al. [57] and is expressed as Eq. (16).

$${\mathrm{R}}_{\mathrm{L}} = 1/ (1 +\mathrm{ b }{\mathrm{C}}_{\mathrm{i}})$$
(14)

where: Ci is the initial concentration of dye ion (mg L−1), while b is the Langmuir constant (L mg−1). As defined by Hall et al. [57], the RL values indicate whether the isotherm is favorable (0 < RL < 1), linear (RL = 1), unfavorable (RL > 1), or irreversible (RL = 0). Therefore, the RL values for MO adsorption onto adsorbents are in the range of 0–1 with an average value of 0.05. As stated in Table 3, the elimination of MO ions was beneficial.

Table 3 Error analysis and adsorption isotherm models constants of MO dye
Full size table
Fig. 8
figure 8

The fitting plot of Langmuir isotherm equation (the initial dye concentrations varied from 5 to 50 mg l−.1 using 0.1 g of adsorbent for 2 h with constant dosages of 0.1 g and 180 rpm)

Full size image

3.4.2 Freundlich

The adsorption equilibrium of MO dye on active and physically processed algal biomass preparations was predicted using the Freundlich data. The Freundlich isotherm equation was used to fit the experimental data, as shown in Fig. 9, and it had a strong correlation (R2 = 0.988). On the basis of adsorption onto a heterogeneous surface, the Freundlich equation was developed [58]. For MO dye onto adsorbent, KF and n parameters were discovered to be 159.2 and 1.12, respectively (Table 3). For favorable adsorption, the Freundlich constant n should be in the range of 1 to 10. Positive binding and heterogeneous adsorption are indicated by n > 1 values [27].

Fig. 9
figure 9

The fitting plot of the Freundlich isotherm equation (the initial dye concentrations varied from 5 to 50 mg l−.1 using 0.1 g of adsorbent for 2 h with constant dosages of 0.1 g and 180 rpm)

Full size image

3.4.3 Temkin

The Temkin isotherm equation predicts that binding energies will be distributed uniformly throughout the population of exterior binding sorption sites. Furthermore, the range and distribution of binding energies should be significantly influenced by the density and distribution of functional groups across both the dye and biosorbent surfaces. The Temkin adsorption isotherm model was selected to determine the adsorption potentials of the adsorbent for adsorbates. Table 1 shows the isotherm parameters. The R2 values obtained for the linear models were close to unity (> 0.759) for the entire set of isotherm models investigated as shown in Fig. 10. As a result of this study, isotherm models appear to be less effective in modeling experimental data. Alternatively, the Temkin isotherm’s bT constant is connected to adsorption energy variation. A positive value of the bT constant suggests an exothermic adsorption reaction, as demonstrated by the value of 24.5 in this study [59].

Fig. 10
figure 10

The fitting plot of the Tempkin isotherm equation (the initial dye concentrations varied from 5 to 50 mg l−.1 using 0.1 g of adsorbent for 2 h with constant dosages of 0.1 g and 180 rpm)

Full size image

3.4.4 Dubinin-Radushkevich

Dubinin-Radushkevich (D-R) isotherm is another isotherm equation that assumed that the sorption curve characteristics are related to the adsorbent’s porosity. Table 3 shows the isotherm parameters qm and K. The linear correlation coefficient is R2 = 0.86 as exhibited in Fig. 11. The average sorption energy E (kJ mol−1) was found to be 10, which is in the energy range of physical sorption reactions. The biomass has a monomolecular adsorption capacity qm of 24.78 mol g−1 [60].

Fig. 11
figure 11

The fitting plot of the Dubinin-Radushkevich isotherm equation (the initial dye concentrations varied from 5 to 50 mg l−.1 using 0.1 g of adsorbent for 2 h with constant dosages of 0.1 g and 180 rpm)

Full size image

3.4.5 Goodness of model fit

Traditional approaches for estimating isotherm variables, such as linear regression equations, appear to provide very good fits to experimental results. To evaluate the fit of isotherm equations to experimental data, a large number of linear regression basin error functions were used to estimate isotherm constants and compare them to less precise linearized analytical results. Furthermore, the standard errors for all variables were utilized to compute the goodness-of-fit for both error analyses [Hybrid fractional error (HYBRID)], the sum of squares of errors (ERRSQ), and the nonlinear chi-square test (X2). As a result, three various error functions were tested experimentally to choose the optimal isotherm model for the experimental data.

Hybrid fractional error

The hybrid fractional error (HYBRID) function is employed as it is more reliable than other error functions and adapts to low concentrations by optimizing absolute deviation versus fractional error. According to the literature, the hybrid error is given by Eq. (11) [50, 51].

$$\mathrm{HYBRID}=\frac{100}{N-P}\sum \left|\frac{{q}_{e,exp}-{q}_{e,calc}}{{q}_{e,exp}}\right|$$
(15)

where: qm represents the isotherm model constant, N represents the number of data points, P represents the number of isotherm parameters, qe represents the equilibrium capacity determined from experimental data, and q represents the average of qe.

The sum of the squares of the errors

The sum of the squares of the errors is given by Eq. (13) below (ERRSQ) [52].

$$\mathrm{ERRSQ}=\sum_{i=1}^{N}{{\left({q}_{e,exp}-{q}_{e,isotherm}\right)}_{i}}^{2}$$
(16)

Nonlinear chi-square test (χ2)

A nonlinear chi-square test is a statistical method for determining the optimum treatment strategy. The chi-square error (χ2) equation is given to be the next equation:

$${X}^{2}=\frac{{\left({q}_{e,isotherm}-{q}_{e,calc}\right)}^{2}}{{q}_{e,isotherm}}$$
(17)

By comparing the error function values, it was discovered that the Freundlich isotherm theory is substantially greater than the other three equations. The Freundlich isotherm model has good correlation coefficients with low values for both Hybrid, ERRSQ, and chi-square, as seen in Table 3.

3.5 Kinetics modeling

To study the governing mechanisms of the sorption mechanism, such as mass transfer and chemical reaction, the pseudo-first-order and pseudo-second-order kinetics models, and the intraparticle diffusion model, were employed to assess the experimental adsorption by A. platensis [14].

3.5.1 Pseudo-first-order kinetics models

When the experimental results for dye elimination were determined using the pseudo-first-order (Eq. (5)), a perfectly straight line was obtained when a graph of ln (qe and qt) and t was produced, suggesting a non-fit on the equation (Fig. 12). For rigorous surface adsorption, the rate variation ought to be equal to the first power of concentration. The initial solute concentration and adsorption rate have a linear relationship because pore diffusion inhibits adsorption. The pseudo-first-order data suit the Lagergren model well, but the adsorption data deviate from the theory after that. As a consequence, the model covers the early phases of rapid adsorption but can be extended to include the complete adsorption process. Additionally, except at a concentration of 90 mg L−1, where the estimated qe values are equal to the observed qe values and the correlation coefficient R2 is rather high (Table 3), the adsorption of MO onto A. platensis is a first-order reaction. The number of pollutant-occupied adsorption sites on the adsorbent surface is compared to the number of unoccupied sites in the pseudo-first-order model [61].

Fig. 12
figure 12

Pseudo-frist-order-kinetic models for the elimination of MO dye onto A. platensis nanoparticles

Full size image

3.5.2 Pseudo-second-order equation

According to the pseudo-second-order, the rate-limiting phase in chemical sorption is valance force through electron sharing or exchange between the adsorbent and adsorbate [62]. If second-order kinetics is applicable, a linear relationship between t/qt and t should be evident in the plot. The intercept and slope of the t/qt vs. t graphs were used to compute K2 and the equilibrium adsorption capacity qe (Fig. 13). With correlation coefficients higher than 0.991 for the second-order kinetic model, the linear plots of t/qt versus t at three initial MO concentrations (15, 90, and 150 mg L−1) demonstrate good agreement between experimental and calculated qe values. This demonstrates that the pseudo-second-order model provided a good correlation for the adsorption of varying initial MO dye concentrations. The pseudo-second-order rate constant (k2) reduced from 24.42 to 0.95 as the initial MO concentration increased from 15 to 90 mg L−1.

Fig. 13
figure 13

Pseudo-second-order-kinetic models for the elimination of MO dye onto A. platensis nanoparticles

Full size image

3.5.3 Intraparticle diffusion

Intra-particle diffusion is the rate-controlling factor in an adsorption system, adsorbate uptake differs with the square root of time [63]. Adsorption rates are usually evaluated by measuring the adsorbent’s adsorption capacity as a function of the square root of time. The relationship plot of qt and t1/2 obtained for MO adsorption on A. platensis nanoparticles in this study does not go to the origin, and two separate regions exist. As a consequence, Eq. (5) and Kdif and C values obtained from the slopes and intercepts of the plot’s linear parts were used to analyze two linear areas individually.

Table 4 and Fig. 14 show R2 values near unity, indicating that this model was used. The intercept C values (Table 4) indicate the thickness of the boundary layer; even as the intercept increases, so does its resistance to exterior mass transfer. The constant C was observed to increase from 0.15 to 48.41 with an increase in dye concentration from 15 to 150 mg L−1, indicating an increase in boundary layer thickness, a decrease in the likelihood of external mass transfer, and an increase in the likelihood of internal mass transfer [64, 65]. Higher initial MO dye concentrations were found to result in a decrease in the constant C, which suggests that the boundary layer thickness has decreased and the likelihood of external mass transfer has increased. Also, the intraparticle diffusion rate constant, Kdif, was in the 0.05–1.95 mg g−1 min−1/2 range and decreased as the initial dye concentration increased from 15 to 90 mg L−1. The plots’ linearity exposed that intraparticle diffusion played a substantial effect on adsorbate uptake through adsorbent [63].

Table 4 Comparison of the first, second-order, and interparticle diffusion adsorption rate constants
Full size table
Fig. 14
figure 14

Interparticle-diffusion-kinetic models for the elimination of MO dye onto A. platensis nanoparticles

Full size image

3.6 Application of A. platensis in MO removal from wastewater

Wastewater having the parameters shown in Table 5, which was previously filtered with a Millipore 0.45 mm filter. To investigate the effect of A. platensis on MO removal, deionized water containing the same dye concentration as wastewater was generated as a control. A wastewater sample was collected from the El-Emoum drain, Alexandria, Egypt, and which comprises numerous industrial sewage and agricultural wastes.

Table 5 Characteristics and application of real wastewater before and after treatment of MO by A. platensis nanoparticles
Full size table

The removal efficiency of MO by A. platensis was assessed using wastewater, and the results are shown in Table 5. In the existence of other metal ions, a dosage of 0.1 g of A. platensis was shown to be sufficient, with extraction efficiency of more than 24.6 and 11.5% for both seawater and wastewater, respectively. The removal efficiency of MO from wastewater increased to 99.24% when compared to the results obtained using deionized water.

This could be due to organic compounds in wastewater being adsorbed onto A. platensis and eliminating a portion of the binding. Organic material and ion complexation in the dye could also reduce MO dye adsorption on A. platensis. In any case, the outcomes demonstrate the viability of using A. platensis as a low-cost adsorbent to extract MO from wastewater. To further show the applicability of A. platensis in extracting MO dye from wastewater, Table 2 compares the maximum capacity of several adsorbents for MO published in the literature. Furthermore, A. platensis have a much better capacity than the other low-cost adsorbents, indicating that it could be a promising low-cost adsorbent used for industrial wastewater treatment.

Table 6 illustrates the adsorption performance A. platensis for MO removal capacity compared with other adsorbents and bio-adsorbents. The results revealed that effective adsorbent compared to various studies on MO removal.

Table 6 Comparison of MO dye adsorption capacity with various adsorbents
Full size table

3.7 Regeneration and reusability study

Industrial applications can benefit from regeneration studies on the possibility of desorbing MO molecules from A. platensis. The solvent desorption technique was used by adding 50 ml of the solution to MO-loaded A. platensis and shaking it at 150 rpm for 3 h at pH 1 and 5 mg L−1. The number of regeneration cycles elevated from one to three, and the effectiveness of MO dye adsorption from A. platensis in synthetic solution decreased from 97.73 to 89.28% (Fig. 15). This may be caused by the insufficient desorption of MO dye that A. platensis has absorbed. The regeneration result shows that A. platensis loses only 8.44% of its adsorbing capacity after three cycles for the synthetic solution due to the decreased biomass amount in the solution and available sites number for adsorption [66]. Furthermore, our research indicated that A. platensis can be regenerated and still had high adsorption effectiveness even after being utilized after three times. A saturated bio-adsorbent must be disposed of and managed in line with the needs of the relevant parties, and it must be marked as hazardous waste after it has significantly decreased in adsorption ability and is no longer reliable for use in the future [67].

Fig. 15
figure 15

Regeneration cycles of A. platensis nanoparticles and the removal percentages of MO dye (by adding 50 ml of the solution to MO-loaded A. platensis at 150 rpm for 3 h at pH 1 and 5 mg L−.1)

Full size image

3.8 Proposed adsorption mechanism

This study showed that the numerous functional groups on the surface of A. platensis biomass, including as –OH and –NH groups, C = O groups and aromatics groups, are substantially dependent on the adsorption of MO dye from aqueous solution by A. platensis biomass. Other research has found that brown algal cell walls contain alginate, a key polymer in blue-green algae algae that provides carboxyl groups. After protonation and deprotonation, the surface of A. platensis functional groups might be charged (negative and positive) or neutral. Besides, the electrostatic affinity between functional groups and the MO dye molecule may describe MO sorption on A. platensis biomass. Moreover, The average ∆G° value for the MO adsorption developed in this work is − 10.1 kJ mol−1, indicating that the dominating mechanism was physical adsorption via a physical process involving weak attraction forces.

4 Conclusions

The objective of this investigation was to see if A. platensis nanoparticles might be utilized as a natural and environmentally acceptable product to remove the methyl orange color from water. The study experimented with various factors such as contact time, initial dye concentration, adsorbent dose, and pH. It was found that the best results were achieved with a low pH of 1 and a concentration of 30 mg L−1. To better understand how the MO dye was being removed from the water by the A. platensis biomass, the adsorption mechanisms were investigated using several analytical techniques including FTIR, BET, and SEM. The results presented that the multipoint BET, single point BET surface area, and BJH adsorption cumulative micropore volume of the A. platensis was 139.83 m2 g─1, 114.373 m2 g−1, and 0.101 cc g─1, respectively. In a batch condition at 20 °C, the adsorption behavior was performed by kinetic and equilibrium isothermal studies. Moreover, the thermodynamic factors showed the exothermic nature and physisorption of the adsorption process, which tends to be spontaneous at lower temperatures. Freundlich, Langmuir, Temkin, and Dubinin-Radushkevich isotherm models were also performed to evaluate the removal of MO dye into nanoparticles of A. platensis. The Freundlich equation, which indicates multilayer adsorption on the heterogeneous surface, provided the best representation of the equilibrium adsorption data. The qe experiment and calculation values for the pseudo-first-order, pseudo-second-order, and interparticle diffusion kinetic models were determined. The results displayed that A. platensis exhibited 99% of MO dye removal. Furthermore, it will aid in the reusability of adsorbents, which may then be employed to adsorb MO dye ions and establish an effective adsorption process. Finally, our work revealed that A. platensis dried nanoparticles are an efficient and appealing biomaterial for MO dye adsorption from synthetic aqueous solution.