Skip to main content
SpringerLink
Log in

A century of Sierpiński–Zygmund functions

  • Survey
  • Published:
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas Aims and scope Submit manuscript

Abstract

Sierpiński–Zygmund (\({{\,\mathrm{SZ}\,}}\)) functions are the maps from \({\mathbb {R}}\) to \({\mathbb {R}}\) that have “as little continuity” as possible. In this work we discuss the history behind their discovery, their constructions through the years, and their generalizations. The presentation emphasizes the algebraic properties of \({{\,\mathrm{SZ}\,}}\) maps and their relation to different classes of generalized continuous-like functions. From the seminal work of Blumberg and the appearance of Sierpiński–Zygmund’s result, we describe the current state of the art of this century-old class of functions and discuss the impact that it has had on several different directions of research. Many typical proofs used in the theory, often in a simplified format never published before, are included in the presented material. Moreover, open problems and new directions of research are indicated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. All birth and death dates we include in this work are publicly available.

  2. Krzysztof Chris Ciesielski (1957–), the first author, is a Polish American mathematician. He received his Ph.D. in 1985 from Warsaw University and the same year moved to the USA. Since 1989 he works at West Virginia University (USA) where he directed, so far, five Ph.D. students, two of which, F. Jordan and K. Płotka, contributed to this story. His research is in foundations of mathematics and, since 2004, in image processing. Around 2006 he began adding his middle name, Chris, in his publications.

  3. Current Ph.D. student of J. B. Seoane-Sepúlveda.

  4. Juan Benigno Seoane-Sepúlveda (1978–), the second author, is a Spanish mathematician. He received his first Ph.D. at the Universidad de Cádiz (Spain) jointly with Universität Karlsruhe (Germany) in 2005. His second Ph.D. was earned at Kent State University (Kent, Ohio, USA) in 2006 under the supervision of Profs. Richard M. Aron and Vladimir I. Gurariy (whose work inspired parts of this story). Since 2010 he’s a professor at Universidad Complutense de Madrid (Spain) and has directed five Ph.D. theses.

  5. Indeed, by Lemma 2.5, a function \(f\in {\mathbb {R}}^{\mathbb {R}}\) belongs to \({{\,\mathrm{SZ}\,}}({{\,\mathrm{{\mathscr {C}}}\,}})\) if, and only if, \(|f\cap g|<{\mathfrak {c}}\) for every continuous g from a \(G_\delta \)-set \(G\subset {\mathbb {R}}\) into \({\mathbb {R}}\). Since any such g has an extension \({\hat{g}}\in {{\,\mathrm{{\mathscr {B}}}\,}}\), we have \({{\,\mathrm{SZ}\,}}({{\,\mathrm{{\mathscr {C}}}\,}})\supset {{\,\mathrm{SZ}\,}}({{\,\mathrm{{\mathscr {B}}}\,}})\).

  6. This property is sometimes referred to as being star-like, see e.g. [56].

  7. The largest in a sense of a size of the minimal cardinality of generating set.

  8. The definition of such a family in [57] additionally assumes that each \(S\in {{\mathcal {S}}}\) has cardinality \(\lambda \). We do not impose it here, but apply this definition only to such families. But the distinction is important, since in the model from Theorem 3.3 there are \(2^{\mathfrak {c}}\) many subsets of \(\omega _1\subset \omega _2\) which, according to our definition, are \({\mathfrak {c}}\)-almost disjoint. Nevertheless, (4) from Theorem 3.2 fails in this model.

  9. Darboux made many important contributions to geometry and mathematical analysis. His alma mater was the Ecole Normale Supérieure (in Paris). He was a biographer of Henri Poincaré (1854–1912). In 1908, he was a plenary speaker at the International Congress of Mathematicians in Rome.

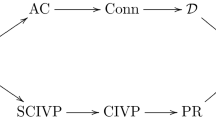
  10. Except that we, additionally, get \({{\,\mathrm{{\mathscr {D}}}\,}}\subset {{\,\mathrm{SCIVP}\,}}= {{\,\mathrm{CIVP}\,}}\).

  11. Young was co-founder and a president of the MAA. He was also editor of the Bulletin of the American Mathematical Society.

  12. Nash shared the 1994 Nobel Memorial Prize in Economic Sciences with game theorists Reinhard Selten and John Harsanyi. In 2015, he also shared the Abel Prize with Louis Nirenberg for his work on nonlinear PDEs.

  13. Stallings’ contributions include a proof, in a 1960 paper, of the Poincaré Conjecture in dimensions greater than six.

  14. By [74, lemma 1], \({{\,\mathrm{dom}\,}}(B)\) has nonempty interior. Thus, by the Baire category theorem, there exists \(n\in {\mathbb {N}}\) for which the same is true for the set \(B_n:=B\cap ({\mathbb {R}}\times [-n,n])\). If J is a nonempty interval contained in \({{\,\mathrm{dom}\,}}(B_n)\) and \(h:J\rightarrow {\mathbb {R}}\) is defined via \(h(x)=\inf \{y:\langle x,y\rangle \in B_n\}\), then h is of Baire class 1. Thus, \(g:=h\upharpoonright C(h)\) is as needed.

  15. The map \(\gamma \) from \(X:= J\cap {{\,\mathrm{dom}\,}}(g)\) into \(g\upharpoonright J\subset {\mathbb {R}}^2\), given as \(\gamma (x):=\langle x, g(x)\rangle \), is continuous and so \(g\upharpoonright J=\gamma [J\cap {{\,\mathrm{dom}\,}}(g)]=\gamma [{\mathrm{cl}}_X(D)]\subset {\mathrm{cl}}_{\mathbb {R}}(\gamma [D])={\mathrm{cl}}_{\mathbb {R}}({\hat{g}}\cap g\upharpoonright J)\).

  16. Current Ph.D. student of Ciesielski.

References

  1. Aizpuru, A., Pérez-Eslava, C., Seoane-Sepúlveda, J.B.: Linear structure of sets of divergent sequences and series. Linear Algebra Appl. 418(2–3), 595–598 (2006). https://doi.org/10.1016/j.laa.2006.02.041

    Article  MathSciNet  MATH  Google Scholar 

  2. Aron, R.M., Bernal González, L., Pellegrino, D.M., Seoane Sepúlveda, J.B.: Lineability: The Search for Linearity in Mathematics. Monographs and Research Notes in Mathematics. CRC Press, Boca Raton (2016)

    MATH  Google Scholar 

  3. Aron, R.M., Gurariy, V.I., Seoane Sepúlveda, J.B.: Lineability and spaceability of sets of functions on \({\mathbb{R}}\). Proc. Am. Math. Soc. 133(3), 795–803 (2005). https://doi.org/10.1090/S0002-9939-04-07533-1

    Article  MathSciNet  MATH  Google Scholar 

  4. Aron, R.M., Conejero, J.A., Peris, A., Seoane-Sepúlveda, J.B.: Uncountably generated algebras of everywhere surjective functions. Bull. Belg. Math. Soc. Simon Stevin 17(3), 571–575 (2010)

    MathSciNet  MATH  Google Scholar 

  5. Aron, R. M., Conejero, J.A., Peris, A., Seoane-Sepúlveda, J.B.: Sums and products of bad functions. In: Function Spaces, Contemporary in Mathemtaics, vol. 435, pp. 47–52. American Mathematical Society, Providence, RI (2007). http://www.ams.org/books/conm/435/

  6. Balcerzak, M., Ciesielski, K., Natkaniec, T.: Sierpiński-Zygmund functions that are Darboux, almost continuous, or have a perfect road. Arch. Math. Logic 37(1), 29–35 (1997). https://doi.org/10.1007/s001530050080

    Article  MathSciNet  MATH  Google Scholar 

  7. Baldwin, S.: Martin’s axiom implies a stronger version of Blumberg’s Theorem. Real Anal. Exchange 16(1), 67–73 (1990/1991)

  8. Banaszewski, K., Natkaniec, T.: Sierpiński–Zygmund functions that have the Cantor intermediate value property. Real Anal. Exchange 24(2), 827–835 (1998/1999)

  9. Bartoszewicz, A., Bienias, M., Gła̧b, S.: Lineability, algebrability and strong algebrability of some sets in \({\mathbb{R}}^{\mathbb{R}}\) or \({\mathbb{C}}^{\mathbb{C}}\). In: Traditional and Present-day Topics in Real Analysis, pp. 213–232. Faculty of Mathematics and Computer Science, University of Łódź, Łódź (2013)

  10. Bartoszewicz, A., Gła̧b, S.: Additivity and lineability in vector spaces. Linear Algebra Appl 439(7), 2123–2130 (2013)

    MathSciNet  MATH  Google Scholar 

  11. Bartoszewicz, A., Bienias, M., Gła̧b, S., Natkaniec, T.: Algebraic structures in the sets of surjective functions. J. Math. Anal. Appl. 441(no. 2), 574–585 (2016). https://doi.org/10.1016/j.jmaa.2016.04.013

  12. Bartoszewicz, A., Gła̧b, S.: Strong algebrability of sets of sequences and functions. Proc. Am. Math. Soc 141(no. 3), 827–835 (2013). https://doi.org/10.1090/S0002-9939-2012-11377-2

  13. Bartoszewicz, A., Gła̧b, S., Pellegrino, D., Seoane-Sepúlveda, J.B.: Algebrability, nonlinear properties, and special functions. Proc. Am. Math. Soc 141(no. 10), 3391–3402 (2013). https://doi.org/10.1090/S0002-9939-2013-11641-2

  14. Bartoszyński, T., Judah, H., Shelah, S.: The Cichoń diagram. J. Symb. Log. 58(2), 401–423 (1993). https://doi.org/10.2307/2275212

    Article  MATH  Google Scholar 

  15. Baumgartner, J.E., Laver, R.: Iterated perfect-set forcing. Ann. Math. Log. 17(3), 271–288 (1979)

    Google Scholar 

  16. Bernal-González, L., Conejero, J.A., Murillo-Arcila, M., Seoane-Sepúlveda, J.B.: \([{\cal{S}}]\)-linear and convex structures in function families. Linear Algebra Appl. 579, 463–483 (2019). https://doi.org/10.1016/j.laa.2019.07.003

    Article  MathSciNet  MATH  Google Scholar 

  17. Bernal-González, L., Pellegrino, D., Seoane-Sepúlveda, J.B.: Linear subsets of nonlinear sets in topological vector spaces. Bull. Am. Math. Soc. (N. S.) 51(no. 1), 71–130 (2014)

  18. Blumberg, H.: New properties of all real functions. Trans. Am. Math. Soc. 24(2), 113–128 (1922). https://doi.org/10.2307/1989037

    Article  MathSciNet  MATH  Google Scholar 

  19. Bradford, J.C., Goffman, C.: Metric spaces in which Blumberg’s theorem holds. Proc. Am. Math. Soc. 11, 667–670 (1960). https://doi.org/10.2307/2034731

    Article  MathSciNet  MATH  Google Scholar 

  20. Brown, J.B.: Connectivity, semi-continuity, and the Darboux property. Duke Math. J. 36, 559–562 (1969)

    MathSciNet  MATH  Google Scholar 

  21. Brown, J.B.: Metric spaces in which a strengthened form of Blumberg’s theorem holds. Fundam. Math. 71(3), 243–253 (1971). https://doi.org/10.4064/fm-71-3-243-253

    Article  MathSciNet  MATH  Google Scholar 

  22. Brown, J.B.: A measure theoretic variant of Blumberg’s theorem. Proc. Am. Math. Soc. 66(2), 266–268 (1977). https://doi.org/10.2307/2040943

    Article  MathSciNet  MATH  Google Scholar 

  23. Brown, J.B., Humke, P., Laczkovich, M.: Measurable Darboux functions. Proc. Am. Math. Soc. 102(3), 603–610 (1988). https://doi.org/10.2307/2047231

    Article  MathSciNet  MATH  Google Scholar 

  24. Brown, J.B., Piotrowski, Z.: Co-Blumberg spaces. Proc. Am. Math. Soc. 96(4), 683–688 (1986). https://doi.org/10.2307/2046325

    Article  MathSciNet  MATH  Google Scholar 

  25. Bruckner, A.M., Ceder, J.G.: Darboux continuity. Jber. Deutsch. Math.-Verein. 67(Abt. 1), 93–117 (1964/1965)

  26. Cauchy, A.-L.: ours d’analyse de l’École Royale Polytechnique. Première partie, Instrumenta Rationis. Sources for the History of Logic in the Modern Age, VII. Cooperativa Libraria Universitaria Editrice Bologna, Bologna (1992). (French)

  27. Ceder, J.: Some examples on continuous restrictions. Real Anal. Exchange 7(1), 155–162 (1981/1982)

  28. Cichoń, J., Morayne, M., Pawlikowski, J., Solecki, S.: Decomposing Baire functions. J. Symb. Log. 56(4), 1273–1283 (1991). https://doi.org/10.2307/2275474

    Article  MathSciNet  MATH  Google Scholar 

  29. Ciesielski, K.: Set Theory for the Working Mathematician, London Mathematical Society Student Texts, vol. 39. Cambridge University Press, Cambridge (1997)

    Google Scholar 

  30. Ciesielski, K.: Set-theoretic real analysis. J. Appl. Anal. 3(2), 143–190 (1997). https://doi.org/10.1515/JAA.1997.143

    Article  MathSciNet  MATH  Google Scholar 

  31. Ciesielski, K.: Decomposing symmetrically continuous and Sierpiński-Zygmund functions into continuous functions. Proc. Am. Math. Soc. 127(12), 3615–3622 (1999). https://doi.org/10.1090/S0002-9939-99-04955-2

    Article  MATH  Google Scholar 

  32. Ciesielski, K.C., Gámez-Merino, J.L., Mazza, L., Seoane-Sepúlveda, J.B.: Cardinal coefficients related to surjectivity, Darboux, and Sierpiński-Zygmund maps. Proc. Am. Math. Soc. 145(3), 1041–1052 (2017). https://doi.org/10.1090/proc/13294

    Article  MATH  Google Scholar 

  33. Ciesielski, K.C., Gámez-Merino, J.L., Pellegrino, D., Seoane-Sepúlveda, J.B.: Lineability, spaceability, and additivity cardinals for Darboux-like functions. Linear Algebra Appl. 440, 307–317 (2014). https://doi.org/10.1016/j.laa.2013.10.033

    Article  MathSciNet  MATH  Google Scholar 

  34. Ciesielski, K., Jastrzbski, J.: Darboux-like functions within the classes of Baire one, Baire two, and additive functions. Topol. Appl. 103(2), 203–219 (2000). https://doi.org/10.1016/S0166-8641(98)00169-2

    Article  MathSciNet  MATH  Google Scholar 

  35. Ciesielski, K., Larson, L., Ostaszewski, K.: \({\cal{I}}\)-density continuous functions. Mem. Am. Math. Soc. 107(515), xiv+133 (1994). https://doi.org/10.1090/memo/0515

  36. Ciesielski, K.C., Martínez-Gómez, M.E., Seoane-Sepúlveda, J.B.: “Big” continuous restrictions of arbitrary functions. Am. Math. Mon. 126(6), 547–552 (2019). https://doi.org/10.1080/00029890.2019.1586263

    Article  MathSciNet  MATH  Google Scholar 

  37. Ciesielski, K., Miller, A.W.: Cardinal invariants concerning functions whose sum is almost continuous. Real Anal. Exchange 20(2), 657–672 (1994)

    MathSciNet  MATH  Google Scholar 

  38. Ciesielski, K., Natkaniec, T.: Algebraic properties of the class of Sierpiński-Zygmund functions. Topol. Appl. 79(1), 75–99 (1997)

    MATH  Google Scholar 

  39. Ciesielski, K., Natkaniec, T.: On Sierpiński-Zygmund bijections and their inverses. Topol. Proc. 22, 155–164 (1997)

    MATH  Google Scholar 

  40. Ciesielski, K.C., Pan, C.-H.: Examples of Sierpiński-Zygmund maps in the class of Darboux-like functions. Banach J. Math. Anal. (2019). https://doi.org/10.1007/s43037-019-00001-9. (posted on 2019, to appear in print)

  41. Ciesielski, K., Pawlikowski, J.: Continuous images of big sets and additivity of \(s_{0}\) under \({{\rm CPA}}_{{\rm prism}}\). Real Anal. Exchange 29(2), 755–762 (2003/2004). https://doi.org/10.14321/realanalexch.29.2.0755

  42. Ciesielski, K., Pawlikowski, J.: The Covering Property Axiom, CPA: A Combinatorial Core of the Iterated Perfect Set Model, Cambridge Tracts in Mathematics, vol. 164. Cambridge University Press, Cambridge (2004)

    MATH  Google Scholar 

  43. Ciesielski, K., Pawlikowski, J.: Small coverings with smooth functions under the covering property axiom. Can. J. Math. 57(3), 471–493 (2005). https://doi.org/10.4153/CJM-2005-020-8

    Article  MathSciNet  MATH  Google Scholar 

  44. Ciesielski, K., Rec law, I.: Cardinal invariants concerning extendable and peripherally continuous functions. Real Anal. Exchange 21(2), 459–472 (1995/1996)

  45. Ciesielski, K.C., Rodríguez-Vidanes, D.L., Seoane-Sepúlveda, J.B.: Algebras of measurable extendable functions of maximal cardinality. Linear Algebra Appl. 565, 258–266 (2019). https://doi.org/10.1016/j.laa.2018.12.017

    Article  MathSciNet  MATH  Google Scholar 

  46. Ciesielski, K. C., Rodríguez-Vidanes, D. L., Seoane-Sepúlveda, J. B.: Additivity coefficients for all classes in the algebra of Darboux-like maps on \({\mathbb{R}}\) (2019) (work in progress)

  47. Ciesielski, K.C., Seoane-Sepúlveda, J.B.: Simultaneous small coverings by smooth functions under the covering property axiom. Real Anal. Exchange 43(2), 359–386 (2018). https://doi.org/10.14321/realanalexch.43.2.0359

    Article  MathSciNet  MATH  Google Scholar 

  48. Ciesielski, K.C., Seoane-Sepúlveda, J.B.: Differentiability versus continuity: restriction and extension theorems and monstrous examples. Bull. Am. Math. Soc. 56(2), 211–260 (2019). https://doi.org/10.1090/bull/1635

    Article  MathSciNet  MATH  Google Scholar 

  49. Cornette, J.L.: Connectivity functions and images on Peano continua. Fundam. Math. 58, 183–192 (1966). https://doi.org/10.4064/fm-58-2-183-192

    Article  MathSciNet  MATH  Google Scholar 

  50. Darboux, G.: Mémoire sur les fonctions discontinues. Ann. Sci. École Norm. Sup. 2(4), 57–112 (1875). (French)

  51. Darji, U.B.: A Sierpiński-Zygmund function which has a perfect road at each point. Colloq. Math. 64(2), 159–162 (1993)

    MathSciNet  MATH  Google Scholar 

  52. Dirichlet, P.G.L.: Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données. J. Reine Angew. Math. 4, 157–169 (1829)

    MathSciNet  Google Scholar 

  53. Eno, P.H., Gurariy, V.I., Seoane-Sepúlveda, J.B.: Some results and open questions on spaceability in function spaces. Trans. Am. Math. Soc. 366(2), 611–625 (2014)

    MathSciNet  MATH  Google Scholar 

  54. Fonf, V.P., Gurariy, V.I., Kadets, M.I.: An infinite dimensional subspace of \(C[0; 1]\) consisting of nowhere differentiable functions. C. R. Acad. Bulg. Sci. 52(11–12), 13–16 (1999)

    MathSciNet  MATH  Google Scholar 

  55. Gámez-Merino, J.L., Muñoz-Fernández, G.A., Sánchez, V.M., Seoane-Sepúlveda, J.B.: Sierpiński-Zygmund functions and other problems on lineability. Proc. Am. Math. Soc. 138(11), 3863–3876 (2010)

    MATH  Google Scholar 

  56. Gámez-Merino, J.L., Muñoz-Fernández, G.A., Seoane-Sepúlveda, J.B.: Lineability and additivity in \({\mathbb{R}}^{{\mathbb{R}}}\). J. Math. Anal. Appl. 369(1), 265–272 (2010)

    MathSciNet  MATH  Google Scholar 

  57. Gámez-Merino, J.L., Seoane-Sepúlveda, J.B.: An undecidable case of lineability in \({\mathbb{R}}^{{\mathbb{R}}}\). J. Math. Anal. Appl. 401(2), 959–962 (2013)

    MathSciNet  MATH  Google Scholar 

  58. Gibson, R.G., Roush, F.: The Cantor intermediate value property. In: Proceedings of the 1982 Topology Conference (Annapolis, Md., 1982). Topol. Proc. 7(1), 55–62 (1982)

  59. Gibson, R. G., Roush, F.: Connectivity functions with a perfect road. Real Anal. Exchange 11(1), 260–264 (1985/1986) [the ninth summer real analysis symposium (Louisville, Ky., 1985)]

  60. Gibson, R.G., Natkaniec, T.: Darboux like functions. Real Anal. Exchange. 22(2), 492–533 (1996/1997)

  61. Goffman, C.: On a theorem of Henry Blumberg. Mich. Math. J. 2, 21–22 (1954)

    MathSciNet  MATH  Google Scholar 

  62. Gurariĭ, V.I.: Subspaces and bases in spaces of continuous functions. Dokl. Akad. Nauk SSSR 167, 971–973 (1966). (Russian)

    MathSciNet  Google Scholar 

  63. Gurariĭ, V.I.: Linear spaces composed of everywhere non-differentiable functions. C. R. Acad. Bulg. Sci. 44(5), 13–16 (1991). (Russian)

    Google Scholar 

  64. Hagan, M.R.: Equivalence of connectivity maps and peripherally continuous transformations. Proc. Am. Math. Soc. 17, 175–177 (1966)

    MathSciNet  MATH  Google Scholar 

  65. Hamel, G.: Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung: \(f (x + y) = f (x) + f (y)\). Math. Ann. 60, 459–462 (1905)

    MathSciNet  MATH  Google Scholar 

  66. Hamilton, O.H.: Fixed points for certain noncontinuous transformations. Proc. Am. Math. Soc. 8, 750–756 (1957)

    MathSciNet  MATH  Google Scholar 

  67. Jasinski, J., Reclaw, I.: Restrictions to continuous and pointwise discontinuous functions. Real Anal. Exchange 23(1), 161–174 (1997/1998)

  68. Jones, F.B., Thomas Jr., E.S.: Connected \(G_{\delta }\) graphs. Duke Math. J. 33, 341–345 (1966)

    MathSciNet  Google Scholar 

  69. Jordan, F.: Cardinal invariants connected with adding real functions. Real Anal. Exchange 22(2), 696–713 (1996/1997)

  70. Jordan, F.: Cardinal numbers connected with adding Darboux-like functions. Ph.D. dissertation, West Virginia University, USA (1998)

  71. Jordan, F.: Generalizing the Blumberg theorem. Real Anal. Exchange 27(2), 423– 439 (2001/2002)

  72. Katafiasz, A., Natkaniec, T.: A new variant of Blumberg’s theorem. Real Anal. Exchange 22(2), 806–813 (1996/1997)

  73. Kechris, A.S.: Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156. Springer, New York (1995)

    Google Scholar 

  74. Kellum, K. R.: Almost continuity and connectivity | sometimes it’s as easy to prove a stronger result. Real Anal. Exchange 8(1), 244–252 (1982/1983)

  75. Kharazishvili, A. B.: On additive absolutely nonmeasurable Sierpiński–Zygmund functions. Real Anal. Exchange 31(2), 553–560 (2005/2006)

  76. Kharazishvili, A.B.: On measurable Sierpiński-Zygmund functions. J. Appl. Anal. 12(2), 283–292 (2006)

    MathSciNet  MATH  Google Scholar 

  77. Kharazishvili, A.B.: Strange Functions in Real Analysis. Pure and Applied Mathematics, vol. 272, 2nd edn. Chapman & Hall/CRC, Boca Raton (2006)

  78. Kharazishvili, A.B., Kirtadze, A.: On the measurability of functions with respect to certain classes of measures. Georgian Math. J. 11(3), 489–494 (2004)

    MathSciNet  MATH  Google Scholar 

  79. Kuczma, M.: An introduction to the theory of functional equations and inequalities, Prace Naukowe Uniwersytetu Śląskiego w Katowicach [Scientific Publications of the University of Silesia], vol. 489, Uniwersytet Śląski, Katowice; Państwowe Wydawnictwo Naukowe (PWN), Warsaw. Cauchy’s equation and Jensen’s inequality; With a Polish summary (1985)

  80. Kunen, K.: Set Theory: An Introduction to Independence Proofs, Studies in Logic and the Foundations of Mathematics, vol. 102. North-Holland Publishing Co., Amsterdam (1983). (reprint of the 1980 original)

  81. Lang, S.: Algebra, Graduate Texts in Mathematics, vol. 211, 3rd edn. Springer, New York (2002)

  82. Lévy, A.: Basic Set Theory. Springer, Berlin (1979)

    MATH  Google Scholar 

  83. Lipecki, Z.: Noncontinuous linear operators and independent linear topologies. Comment. Math. (Prace Mat.) 38, 53–62 (1998)

    MathSciNet  MATH  Google Scholar 

  84. López Pellicer, M.: A note on the Blumberg property. Rev. Real Acad. Cienc. Exact. Fís. Natur. Madrid 78(1–2), 147–150 (1984). (Spanish, with English summary)

  85. Maximoff, I.: Sur les fonctions ayant la propriété de Darboux. Prace Mat. Fiz. 43, 241–265 (1936)

    MATH  Google Scholar 

  86. Miller, A.W.: Mapping a set of reals onto the reals. J. Symb. Log. 48(3), 575–584 (1983)

    MathSciNet  MATH  Google Scholar 

  87. Mycielski, J.: Independent sets in topological algebras. Fundam. Math. 55, 139–147 (1964). https://doi.org/10.4064/fm-55-2-139-147

    Article  MathSciNet  MATH  Google Scholar 

  88. Nash, J.: Generalized Brouwer theorem. Bull. Am. Math. Soc. 62(1), 76 (1956)

    Google Scholar 

  89. Natkaniec, T.: Almost continuity. Real Anal. Exchange 17(2), 462–520 (1991/1992)

  90. Natkaniec, T.: New cardinal invariants in real analysis. Bull. Pol. Acad. Sci. Math. 44(2), 251–256 (1996)

    MathSciNet  MATH  Google Scholar 

  91. Natkaniec, T., Rosen, H.: An example of an additive almost continuous Sierpiński–Zygmund function. Real Anal. Exchange 30(1), 261–265 (2004/2005)

  92. Natkaniec, T., Rosen, H.: Additive Sierpiński–Zygmund functions. Real Anal. Exchange 31(1), 253–269 (2005/2006)

  93. Piotrowski, Z., Szymański, A.: Concerning Blumberg’s theorem. Houst. J. Math. 10(1), 109–115 (1984)

    MathSciNet  MATH  Google Scholar 

  94. Płotka, K.: Sum of Sierpiński-Zygmund and Darboux like functions. Topol. Appl. 122(3), 547–564 (2002). https://doi.org/10.1016/S0166-8641(01)00184-5

    Article  MATH  Google Scholar 

  95. Płotka, K.: Darboux-like functions within the class of Hamel functions. Real Anal. Exchange 34(1), 115–125 (2009)

    MathSciNet  MATH  Google Scholar 

  96. Płotka, K.: Algebraic structures within subsets of Hamel and Sierpiński-Zygmund functions. Bull. Belg. Math. Soc. Simon Stevin 22(3), 447–454 (2015)

    MathSciNet  MATH  Google Scholar 

  97. Recław, I.: Restrictions to continuous functions and Boolean algebras. Proc. Am. Math. Soc. 118(3), 791–796 (1993)

    MathSciNet  MATH  Google Scholar 

  98. Roberts, J.H.: Zero-dimensional sets blocking connectivity functions. Fundam. Math. 57, 173–179 (1965)

    MathSciNet  MATH  Google Scholar 

  99. Rosen, H., Gibson, R. G., Roush, F.: Extendable functions and almost continuous functions with a perfect road. Real Anal. Exchange 17(1), 248–257 (1991/1992)

  100. Rosłanowski, A., Shelah, S.: Measured creatures. Isr. J. Math. 151, 61–110 (2006). https://doi.org/10.1007/BF02777356

    Article  MathSciNet  MATH  Google Scholar 

  101. Seoane-Sepúlveda, J. B.: Chaos and lineability of pathological phenomena in analysis. Ph.D. thesis, Kent State University, Pro-Quest LLC, Ann Arbor, MI (2006)

  102. Shelah, S.: Possibly every real function is continuous on a non-meagre set. Publ. Inst. Math. (Beograd) (N. S.) 57(71), 47–60 (1995). (Đuro Kurepa memorial volume)

  103. Shinoda, J.: Some consequences of Martin’s axiom and the negation of the continuum hypothesis. Nagoya Math. J. 49, 117–125 (1973)

    MathSciNet  MATH  Google Scholar 

  104. Sierpiński, W., Zygmund, A.: Sur une fonction qui est discontinue sur tout ensemble de puissance du continu. Fundam. Math. 4, 316–318 (1923)

    MATH  Google Scholar 

  105. Stallings, J.: Fixed point theorems for connectivity maps. Fundam. Math. 47, 249–263 (1959)

    MathSciNet  MATH  Google Scholar 

  106. Steprāns, J.: Decomposing Euclidean space with a small number of smooth sets. Trans. Am. Math. Soc. 351(4), 1461–1480 (1999)

    MathSciNet  MATH  Google Scholar 

  107. Von Neumann, J.: Ein System algebraisch unabhängiger Zahlen. Math. Ann. 99, 134–141 (1928). https://doi.org/10.1007/BF01459089. (German)

  108. White Jr., H.E.: Topological spaces in which Blumberg’s theorem holds. Proc. Am. Math. Soc. 44, 454–462 (1974). https://doi.org/10.2307/2040456

    Article  MathSciNet  MATH  Google Scholar 

  109. White Jr., H.E.: Topological spaces in which Blumberg’s theorem holds. II. Illn. J. Math. 23(3), 464–468 (1979)

    MathSciNet  MATH  Google Scholar 

  110. Whyburn, G.T.: Connectivity of peripherally continuous functions. Proc. Natl. Acad. Sci. USA 55, 1040–1041 (1966)

    MathSciNet  MATH  Google Scholar 

  111. Young, J.: A theorem in the theory of functions of a real variable. Rend. Circ. Mat. Palermo 24, 187–192 (1907)

    MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Prof. Dr. Tomasz Natkaniec for his very careful reading of an earlier version of this manuscript, especially for many insightful comments and suggestions. We also like to express our gratitude to Dr. George Blumberg, Dr. Larisa Lev Altshuler, and the Real Analysis Exchange journal for their help in providing the photographs from Figs. 1, 4, and 3 , respectively. J. B. Seoane-Sepúlveda was supported by Grants MTM2015-65825-P and PGC2018-097286-B-I00.

Author information

Authors and Affiliations

  1. Department of Mathematics, West Virginia University, Morgantown, WV, 26506-6310, USA

    K. C. Ciesielski

  2. Department of Radiology, MIPG, University of Pennsylvania, Philadelphia, PA, 19104-6021, USA

    K. C. Ciesielski

  3. Instituto de Matemática Interdisciplinar (IMI), Departamento de Análisis Matemático y Matemática Aplicada, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, Plaza de Ciencias 3, 28040, Madrid, Spain

    J. B. Seoane-Sepúlveda

Authors
  1. K. C. Ciesielski
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. B. Seoane-Sepúlveda
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. B. Seoane-Sepúlveda.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ciesielski, K.C., Seoane-Sepúlveda, J.B. A century of Sierpiński–Zygmund functions. RACSAM 113, 3863–3901 (2019). https://doi.org/10.1007/s13398-019-00726-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13398-019-00726-0

Keywords

Mathematics Subject Classification

Search

Navigation