Skip to main content
SpringerLink
Log in

Shrinking projection methods involving inertial forward–backward splitting methods for inclusion problems

  • Original Paper
  • Published:
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas Aims and scope Submit manuscript

Abstract

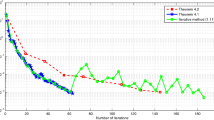
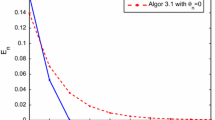
In this paper, we propose a modified forward–backward splitting method using the shrinking projection and the inertial technique for solving the inclusion problem of the sum of two monotone operators. We prove its strong convergence under some suitable conditions in Hilbert spaces. We provide some numerical experiments including a comparison to show the implementation and the efficiency of our method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Alvarez, F., Attouch, H.: An inertial proximal method for monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 9, 3–11 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  2. Baillon, J.B., Haddad, G.: Quelques proprietes des operateurs angle-bornes et cycliquement monotones. Isr. J. Math. 26, 137–150 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bauschke, H.H., Combettes, P.L.: A weak-to-strong convergence principle for Fejér-monotone methods in Hilbert spaces. Math. Oper. Res. 26, 248–264 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics. Springer, New York (2011)

    Book  MATH  Google Scholar 

  5. Browder, F.E.: Nonexpansive nonlinear operators in a Banach space. Proc. Natl. Acad. Sci. USA 54, 1041–1044 (1965)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cholamjiak, P.: A generalized forward-backward splitting method for solving quasi inclusion problems in Banach spaces. Numer. Algor. 8, 221–239 (1994)

    Article  Google Scholar 

  7. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dang, Y., Sun, J., Xu, H.: Inertial accelerated algorithms for solving a split feasibility problem. J. Ind. Manag. Optim. https://doi.org/10.3934/jimo.2016078

  9. Dong, Q.L., Yuan, H.B., Cho, Y.J., Rassias, Th.M.: Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. https://doi.org/10.1007/s11590-016-1102-9

  10. Douglas, J., Rachford, H.H.: On the numerical solution of the heat conduction problem in 2 and 3 space variables. Trans. Am. Math. Soc. 82, 421–439 (1956)

    Article  MathSciNet  MATH  Google Scholar 

  11. Eshita, K., Takahashi, W.: Approximating zero points of accretive operators in general Banach spaces. J. Fixed Point Theory Appl. 2, 105–116 (2007)

    MathSciNet  MATH  Google Scholar 

  12. Kim, T.H., Xu, H.K.: Strongly convergence of modified Mann iterations for with asymptotically nonexpansive mappings and semigroups. Nonlinear Anal. 64, 1140–1152 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  13. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  14. López, G., Martín-Marquez, V., Wang, F., Xu, H.K.: Forward-backward splitting methods for accretive operators in Banach spaces. Abstr. Appl. Anal. Art ID 109236 (2012)

  15. Lorenz, D., Pock, T.: An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51, 311–325 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Moudafi, A., Oliny, M.: Convergence of a splitting inertial proximal method for monotone operators. J. Comput. Appl. Math. 155, 447–454 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  17. Nakajo, K., Takahashi, W.: Strong and weak convergence theorem by an improved splitting method. Commun. Appl. Nonlinear Anal. 9, 99–107 (2002)

    MathSciNet  MATH  Google Scholar 

  18. Nakajo, K., Takahashi, W.: Strongly convergence theorems for nonexpansive mappings and nonexpansive semigroups. J. Math. Anal. Appl. 279, 372–379 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  19. Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O(1/k^2)\). Dokl. Akad. Nauk SSSR 269, 543–547 (1983)

    MathSciNet  Google Scholar 

  20. Passty, G.B.: Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 72, 383–390 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  21. Peaceman, D.H., Rachford, H.H.: The numerical solution of parabolic and elliptic differentials. J. Soc. Ind. Appl. Math. 3, 28–41 (1955)

    Article  MathSciNet  MATH  Google Scholar 

  22. Polyak, B.T.: Introduction to Optimization. Optimization Software, New York (1987)

    MATH  Google Scholar 

  23. Polyak, B.T.: Some methods of speeding up the convergence of iterative methods. Zh. Vychisl. Mat. Mat. Fiz. 4, 1–17 (1964)

    MathSciNet  Google Scholar 

  24. Rockafellar, R.T.: On the maximality of subdifferential mappings. Pac. J. Math. 33, 209–216 (1970)

    Article  MATH  Google Scholar 

  25. Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14, 877–898 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  26. Takahashi, W.: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama (2000)

    MATH  Google Scholar 

  27. Takahashi, W., Takeuchi, Y., Kubota, R.: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 341, 276–286 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  28. Tseng, P.: A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 38, 431–446 (2000)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

S.A. Khan would like to thank BITS-Pilani, Dubai Campus. S. Suantai was supported by Chiang Mai University. W. Cholamjiak would like to thank the Thailand Research Fund under the Project MRG6080105 and University of Phayao.

Author information

Authors and Affiliations

  1. Department of Mathematics, BITS-Pilani, Dubai Campus, P.O. Box 345055, Dubai, UAE

    Suhel Ahmad Khan

  2. Center of Excellence in Mathematics and Applied Mathematics, Department of Mathematics, Faculty of Science, Chiang Mai University, Chiang Mai, 50200, Thailand

    Suthep Suantai

  3. School of Science, University of Phayao, Phayao, 56000, Thailand

    Watcharaporn Cholamjiak

Authors
  1. Suhel Ahmad Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Suthep Suantai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Watcharaporn Cholamjiak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Watcharaporn Cholamjiak.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khan, S.A., Suantai, S. & Cholamjiak, W. Shrinking projection methods involving inertial forward–backward splitting methods for inclusion problems. RACSAM 113, 645–656 (2019). https://doi.org/10.1007/s13398-018-0504-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13398-018-0504-1

Keywords

Mathematics Subject Classification

Search

Navigation