Introduction

Internationally, curriculum expectations indicate that as young students progress through primary school, they need to build capabilities in both critical thinking and mathematical thinking. In Australia, the term critical thinking is referred to in both the Australian National Curriculum (ACARA, 2014) and the Early Years Learning Framework (DEEWR, 2022) with an expectation that learning experiences are provided to support young students to develop this thinking from before school settings through to the end of primary school across a range of disciplines (Ab Kadir, 2018; Heard et al., 2020). As such, critical thinking is not seen as discipline specific but rather a general capability that is embedded in all subject areas, including mathematics.

Critical thinking is found to be a necessary requirement in both education and employability (Heard et al., 2020; National Council of Teachers of Mathematics (NCTM), 2000a, b; Urib-Enciso et al., 2017). Critical thinking is defined as process skills, qualities, competencies and characteristics that help individuals to analyse a situation and make judgements (Elder & Paul, 2020; Lai, 2011; Lipman, 1987; Siswono, 2010; Sternberg, 1986). Internationally, curriculum and policy directions have embedded critical thinking as a key skill to support students to become prepared for the twenty-first century (Urib-Enciso et al., 2017). In addition, research evidences that twenty-first-century skills that are underpinned by critical thinking are required for workforce preparedness and long-term economic success (Burrus et al., 2013; Rios et al., 2020). Despite this, presently, there is little understanding of how critical thinking presents in young students.

Mathematics is a required subject area across levels of education. It can be defined as knowledge, skills, understandings and procedures that require an individual to interpret mathematical content of patterns, like number and space (Animasaun, 2021).Curriculum documents internationally and locally identify the necessity of mathematics for teaching and the need to acquire  mathematical thinking processes. However, the embedding of mathematical thinking as a theme in curriculum documents varies. For example, the American National Council of Teachers of Mathematics (Ferrini-Mundy, 2000) includes the processes of problem solving, reasoning and proof, communication, connections and representations, whereas the Singaporean Mathematics Framework identifies five areas of mathematical proficiency. These are conceptual understanding, procedural fluency, strategic competence, adaptive reasoning and productive disposition (Groves, 2012). The Australian Curriculum: Mathematics includes the following proficiency (process) strands: understanding, fluency, problem solving and reasoning, which are at the centre of the curriculum.

Mathematical thinking is deemed an important construct that underpins one’s ability to solve problems; however, Australian students continue to underperform in both international and national mathematical benchmarks. In comparison to other countries, Australian students’ mathematical performance has at best plateaued and in some cases has declined over recent years (McGaw et al., 2020; Thomson et al., 2020). This decline is particularly prevalent in the area of mathematical thinking with Australian students underperforming in the cognitive domains of knowing and applying; however, data suggests an increase in Australian students reasoning ability in the Trends in International Mathematics and Science Study (TIMSS) (Thomson et al., 2020). Thus, overall, Year 4 students have demonstrated no change in their mathematics achievement in TIMSS between 2015 and 2019, with 70% attaining national proficiency standards which is less than the international medium (Thomson et al., 2020). While mathematical thinking appears to contribute to the decline in mathematics performance, we argue in this paper that there are also implications for that application of critical thinking in this discipline area. The two types of thinking, critical and mathematical, need to be more closely considered in mathematics, with strong foundations formed early in a child’s schooling.

While there is considerable research that supports that many young students are mathematically competent prior to entering formal schooling (Clarke et al., 2006; Clements & Sarama, 2011; Hunting et al., 2009; MacDonald & Carmichael, 2018; Papic & Mulligan, 2005; Perry et al., 2015; Scammacca et al., 2020) and mathematical thinking begins at a young age (Bobis et al., 2005; Doig & Ompok, 2010; Sarama & Clements, 2009), there is little understanding between the relationship of mathematical thinking and critical thinking for young learners. There are a number of inconsistencies in and overlaps between both critical thinking and mathematical thinking definitions in the research literature and curriculum documents. In this paper, we address this gap by drawing on the research literature pertaining to critical thinking and mathematical thinking to conceptualise and define the term critical mathematical thinking (CMT). This new term (CMT) is then further conceptualised to present the critical mathematical thinking conceptual framework, presented in the following sections. Data presented in this paper is analysed in light of the critical mathematical thinking conceptual framework to provide evidence of the types of critical mathematical thinking young students displayed as they entered formal schooling. These data support the final reconceptualization of the framework to present the critical mathematical thinking framework for young students.

Conceptualising critical mathematical thinking

For the larger study, a review of the seminal literature pertaining to the broad areas of critical thinking and mathematical thinking was conducted (Monteleone, 2021). The review of both sets of literature provided an opportunity to blend critical and mathematical thinking to establish an initial literature informed conceptual framework for defining critical mathematical thinking. It is important to note that in this context, critical mathematical thinking is not a term pertaining to critical mathematical education or mathematics for social justice (Skovsmose, 1994), but is a focus on applying critical thinking within a mathematical context. The following sections present the analysis of the themes (overarching recurring terms) and sub-themes (secondary terms aligned to the overarching theme) that emerged across the critical thinking and mathematical thinking literature to develop an initial conceptual framework of critical mathematical thinking.

Themes pertaining to critical thinking

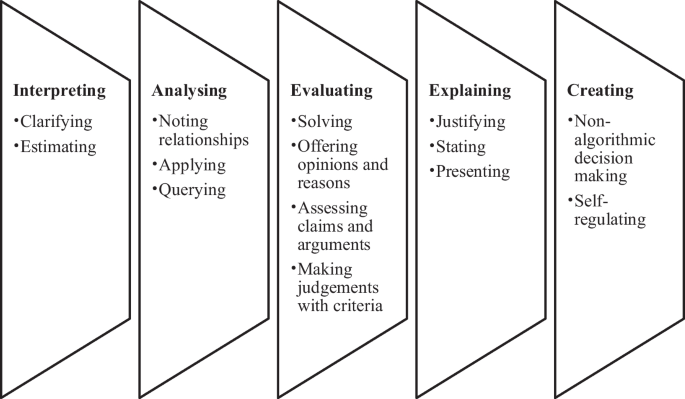
The term, critical thinking, has been explored by many researchers, for example, Davies (2006), Ennis (1992), and Facione (1990), and primarily within the “critical thinking movement” in the USA. The definition is complicated as critical thinking often encapsulates: a judgement; a sceptical and interim view of knowledge, a simple innovation, a way to make sense of texts; rationality, the adoption of an ethical and activist stance and self-reflexivity (Moore, 2013). Since the early critical thinking movement, research in this space has primarily focused on skills, qualities, competencies and characteristics of individuals across a range of disciplines including philosophy, psychology and education (Heard et al., 2020). Siswono (2010, p. 19) states that, “critical thinking is thinking that examines, relates, and evaluates all aspects of a situation or problem”. While there is no consensus on terms used to define critical thinking, it is apparent that there are five recurring themes referred to in the literature describing the cognitive skills or dispositions to represent critical thinking. These five themes are (i) interpreting, (ii) analysing, (iii) evaluating, (iv) explaining and (v) creating. Additionally, when examining the literature, it appeared that the themes were not hierarchical in nature. The following examines these five themes pertaining to critical thinking.

Interpreting

Critical thinking experts include interpreting as a key indicator of critical thinking ability (Ellerton, 2018; Ennis, 2013; Facione & Facione, 2008; Watson & Glaser, 2002). According to Watson and Glaser (2002), interpreting is when an individual can form a logical judgement about conclusions generated. Facione (2011) states that ideal critical thinkers make decisions, which can result in interpretation. To further position how a critical thinker uses the skill of interpreting, the literature reviewed elaborates on interpreting to include sub-themes of assessing (Facione, 2011), categorising (Ellerton, 2018; Facione, 2011), decoding (Facione, 2011), clarifying (Facione, 2011) and identifying (Facione, 2011). The seminal work of Lipman (1987) provided associated sub-themes for good thinking (ways to transition from ordinary to critical thinking). He explains that an individual can interpret and defend their thinking with the use of particular skills. These sub-themes include, assuming, classifying and estimating (Lipman, 1987, 2003). According to Lipman (2003), the use of these sub-themes supports an individual to transition from ordinary thinking to good thinking and allows one to provide sufficient reasons to support their opinions. To build on the sub-themes identified, Siswono (2010) suggests sense making (interpreting) requires examining, remembering and understanding the situation at hand. The theme and sub-themes identify dispositions of an ideal critical thinker to apply interpreting across a range of learning areas.

Analysing

Analysing is found to be a further crucial component associated with critical thinking. Facione (2011) includes analysing as a core critical thinking skill in his definition, referring to analysing as both a cognitive skill and affective disposition. Lai (2011) defines analysing to include the analysis of arguments, judging, making inferences (inductive and deductive reasoning) and solving problems. Literature pertaining to analysing has identified a myriad of sub-themes that represent components of analysing in critical thinking (for example, Facione, 1990, 2011; Lai, 2011; Lipman, 1987; Siswono, 2010). The sub-themes identified have primarily emerged from a systematic review conducted by The American Philosophical Association (Facione, 1990) whereby dispositions that constitute critical thinking are identified in the following sub-themes: applying, conjecturing, drawing conclusions, hypothesising, inferring and noting relationships.

Evaluating

Evaluating is another inter-connected theme associated with critical thinking. This theme often occurs when someone evaluates their thought processes and evaluates their decision or the efficacy of their problem-solving technique (Alsaleh, 2020). Empirical evidence confirms critical thinking dispositions associated with evaluating support students to think critically (Facione & Facione, 2008). The most commonly cited dispositions (sub-themes) include assessing claims and making judgements (Facione, 1990), offering opinions and reasons (Lipman, 1987), making judgements with criteria (Lai, 2011; Lipman, 1987) and querying evidence (Facione, 1990). According to Bailin (2002), evaluating would be evident during domain-specific learning and can be transferable from one domain to another.

Explaining

Ideal critical thinkers use explaining to broaden their thinking. However, it is important to note that explaining on its own might not constitute critical thinking. Fisher (2011, p. 24) states that “working out an explanation” is more advanced than explaining something to another person. Similarly, Halpern (2013) states that providing reasons for the decisions made as well as the depth of detail explained would signify critical thinking. To further position explaining within critical thinking, sub-themes were identified, mainly by the seminal literature of Facione (1990). In particular, stating, presenting and justifying promote an individual’s skill to think critically. According to Facione (2011), using the sub-themes allows for someone to explain their thinking and the process they undertook to arrive at the judgement.

Creating

Innovative thinking or novel ideas are often exhibited when someone is creating (Facione, 2011). Creating or creative thinking is also aligned with critical thinking (Lipman, 1987). Siswono (2010, p. 548) distinguishes creative thinking as “thinking that consists of non-algorithmic decision making”. Non-algorithmic decision-making is considered a complex approach to thinking where there are many possible solutions (Miri et al., 2007; Resnick, 1987). Lewis and Smith (1993) highlight higher-order thinking as a broader term that encapsulates “problem solving, critical thinking, creative thinking, and decision making” (p. 136). Sub-themes that an individual can apply to demonstrate creating are associated with evaluating and decision-making. One such sub-theme is self-regulating. Self-regulating is an action, similar to non-algorithm decision-making, whereby an individual self-evaluates their own inferences (Facione, 1990; Resnick, 1987). An individual that demonstrates self-regulating considers ways to revisit or review their learning prior to making final decisions. A self-regulator would consider conflicting conclusions or a review of their evidence (Facione, 2011). Sternberg (1986) identifies non-algorithmic decision-making as an element of critical thinking through his definition, “mental processes, strategies, and representations people use to solve problems, make decisions, and learn new concepts” (Sternberg, 1986, p. 3).

Themes pertaining to young students’ mathematical thinking

There is a range ofliterature associated with mathematical thinking and mathematical understanding in the early years and primary years. What is prevalent in the literature is that in order for young students to engage in mathematical thinking, young students require multiple learning opportunities as well as a range of strategies. However, the strategies in the mathematical thinking literature show some commonality to the critical thinking literature reviewed above. For the purpose of this paper, we have aligned the mathematics literature to the critical thinking themes (cf. Monteleone, 2021). First, within the mathematical thinking literature, there was robust evidence of the two themes evaluating and explaining together with additional sub-themes associated with each of these themes. Second, while the two themes interpreting, and analysing, were not strong themes across the mathematical literature, there were additional identified sub-themes that contributed to these themes. Finally, there was no evidence of the theme creating within this review of the literature pertaining to mathematical thinking in the primary and early years. For these reasons, the next section focusses on further illuminating the themes and sub-themes associated with evaluating and explaining and additional identified sub-themes related to interpreting and analysing from the mathematics thinking literature.

Evaluating and explaining

The notion of young students evaluating their thinking is seen as central to thinking mathematically. For example, inviting students to evaluate a claim, thought processes or elaborate on an observation are identified by Cengiz et al. (2011) as key to extending students’ mathematical thinking. Additionally, a mathematical thinking framework created by Williams (2000) and extended by Wood et al. (2006) presents categorisations which increase in complexity that ultimately allow a student to evaluate their mathematical thinking. These researchers suggest that in order for students to effectively evaluate their mathematical thinking, they must first comprehend the problem, progress through applying, analysing and synthesising and finally engage in evaluating (Wood et al., 2006). This progression appears to align with the notion of evaluating, as evaluating is identified as a problem-solving technique or solution process in the critical thinking literature (Alsaleh, 2020). Similarly, Cengiz et al. (2011) study considers the type of learning that can support students to evaluate their mathematical thinking. It appears that during classroom discussions, the theme of evaluating dominated students’ responses (Cengiz et al., 2011; Franke & Kazemi, 2001; Wood et al., 2006). Additionally, the mathematical thinking literature agreed that making judgements with criteria (Cengiz et al., 2011), solving; (Francisco & Maher, 2005) and offering their opinions with reasons (Cengiz et al., 2011) were sub-themes of evaluating. Findings from these studies also indicate that the skill of evaluating occurs when the tasks included mathematical problems that allow students to identify mathematical language and make connections with other mathematical concepts. Thus, it is evidenced that the types of tasks set and classroom discussions that occurred contribute to students’ ability to evaluate their thought process and their problem-solving techniques.

Explaining is considered a key mathematical thinking theme often aligned with literature pertaining to reasoning or justifying, focusing on students explaining the “how” and “why” (reasoning, justifying) rather than the “what” (stating, presenting), which aligned to the critical thinking literature. At times within the literature, the terms reasoning and justifying were seen as interchangeable, and other times, they were separated with distinct features. In addition, the definition of the terms seemed to closely align with each study’s aims and methodology (e.g., Diezmann et al., 2001; Melhuish et al., 2020; Wood et al., 2006). However, across the definitions, there are common features. These include defending solutions, providing evidence, making conjectures and presenting logical argument. Studies that focused on students’ reasoning or justifying have also identified that the way the learning experience is framed can provide a platform for young students to reason and justify (Anthony et al., 2015; Hunter & Anthony, 2011; Papandreou & Tsiouli, 2020; Papic et al., 2009; Vale et al., 2017).

Findings from these studies ascertained that a focus on mathematical practices over time that promote and scaffold student participation, in particular opportunities for talk, resulted in students explaining their own mathematical ideas and other students’ ideas and solutions more regularly in class (Cengiz et al., 2011; Hufferd-Ackles et al., 2004; Hunter & Anthony, 2011). These findings further support the notion that the types of tasks set and the classroom discussions that occur are crucial to allowing students to explain and evaluate their own and other students’ mathematical thinking.

Interpreting and analysing

The mathematical thinking literature review also agreed that the sub-themes that support students to interpret the mathematics include estimating (Clarke & Kamii, 1996; Clements & Sarama, 2020; Lambdin & Walcott, 2007; Sowder, 1992), remembering (Cengiz et al., 2011; Fraivillig et al., 1999) and understanding (Bobis et al., 2005; Cengiz et al., 2011; Fraivillig et al., 1999; Jacobs et al., 2010; Mulligan et al., 2020). From a mathematical thinking perspective, estimating has progressed from a simple “guess” to a sophisticated process required to interpret mathematics (Clements & Sarama, 2020). Estimating is evidenced across a range of mathematical concepts: (1) measurement (e.g., estimating the length of a room), (2) numerosity (e.g., estimating the number of people on a bus) and (3) mathematical operations (e.g., estimating how much 12 × 20 is) (Sowder, 1992). Remembering has been found to build on students already established mathematical thinking and to then extend their thinking to include new information (Fraivillig et al., 1999). Similarly, understanding has been identified as a strategy to assist students’ and further challenge students to interpret their mathematical thinking (Fraivillig et al., 1999) and transfer their understandings to other mathematical concepts (Mulligan et al., 2015). Therefore, based on the mathematical thinking literature, a student can interpret (make sense of the mathematics) by using the sub-themes of estimating, remembering and understanding.

Adding on to the already identified sub-themes associated with analysing, the review of the mathematical thinking literature evidenced that the sub-themes noting relationships (Papandreou & Tsiouli, 2020) and grasping principles (Fennema et al., 1998) support young students’ mathematical thinking. While noting relationships was also evidenced in the critical thinking literature, a mathematical thinking perspective by Papandreou and Tsiouli (2020) highlighted how children’s use of representations (blocks, illustrations, written work, body movement or gestures) during mathematics free time provided opportunities for young students to note relationships and grasp principles. Thus, to grasp principles is an additional sub-theme that emerged from this review. Fennema et al. (1998) found that when students used a variety of ways to display their mathematical understandings, they were able to grasp principles and apply these principles to tackle more complex mathematical problems as they progressed through the grades. Although these two sub-themes, noting relationships and grasping principles, are identified as separate terms in the mathematical thinking literature, they both assist students to analyse their mathematical thinking.

The themes and sub-themes cited in accordance with the critical thinking and mathematical thinking literature provided five themes with several associated sub-themes. Table 1 presents themes pertaining to critical thinking and mathematical thinking. The review of literature identified thirty sub-themes across the critical thinking and mathematical thinking literature. At times, mathematical thinking sub-themes were categorised with critical thinking themes, for example, the sub-theme of grasping principles (mathematical thinking) is under the theme of analysing (critical thinking). This is due to the way the sub-theme was described in the literature. Many sub-themes are associated with critical thinking (presented in column 2); however, some sub-themes were present in both sets of literature (presented in column 3) with only two emerging solely from the mathematical thinking literature review (presented in column 4).

Table 1 Critical mathematical thinking themes and sub-themes
Full size table

The review and synthesise of the literature pertaining to both mathematical thinking and critical thinking have led to the amalgamation of the terms as critical mathematical thinking (CMT) and the development of a literature informed conceptual framework to situate the construct CMT. There is little research to suggest that the term CMT exists as a notion, nor was it evident that there had previously been a conceptualization of CMT as a framework. Thus, the review of literature provided an opportunity to blend critical thinking and mathematical thinking to provide a literature informed conceptual framework for defining the term CMT which is then applied to understand the CMT capabilities presented by young students as they enter formal schooling.

Research design

The data reported in this paper are derived from a larger mixed method study. The larger study (Monteleone, 2021), which included 161 students, aimed to investigate CMT in young students and the teaching actions/questions that help young students to exhibit their CMT. The data in this paper reports on the qualitative student data of the larger study. The research question addressed in this paper includes what are the CMT capabilities young students exhibit as they begin formal schooling? As the participants were young students, and the purpose was to identify their CMT capabilities, the data collection process included a task-based clinical interview. The conceptual framework presented in Table 1 forms the basis of the qualitative component of the study and is used as a lens to analyse the student data.

Participants

In total, 161 kindergarten students, aged between 5 years and 1 month to 6 years and 8 months of age, participated in the larger study (Monteleone, 2021). These students were from three primary schools located in New South Wales Australia all within an urban setting in southern Sydney. The schools had similar demographics and ranges in the Index of Community Socio-Educational Advantage (ICSEA) level (1092–1112). The ICSEA score above 1000 indicates schools that are considered socio-economically advantaged. Finally, the average Numeracy National Assessment Program—Literacy and Numeracy (NAPLAN) results were similar and above the Australian average results. Informed written consent was obtained from principals, teachers, parents and students before data collection commenced.

High CMT students

As the larger study moved through different stages of data collection, including quantitative measures, the participants were narrowed from 161 students to include 16 students that displayed high levels of CMT in alignment with the literature informed conceptual framework. These 16 students are the focus of this paper and were identified as high CMT students. The students were selected across the three schools with four students from School A (25% of the sample from School A), five students from School B (32% of the sample from School B) and seven students from School C (43% of the sample from School C) (16 students in total). In summary of the 16 high CMT students, nine were male, and seven were female.

Data collection

The larger mixed method study included quantitative measures that assisted in the purposeful selection of participants. For the purpose of this paper, findings from the one-on-one task-based interview are drawn on to evidence and illustrate the types of critical mathematical thinking of young learners. All 16 high CMT students participated in the video recorded interviews conducted by the researcher. On average, each interview was 20 min.

Task-based one-on-one interviews

A task-based one-on-one clinical interview schedule, the Critical Mathematical Thinking Learning Experiences (CMTLE) consisting of eight learning experiences, was used with the high CMT students (n = 16). The process of a clinical interview has roots in Piaget’s methode clinique (Hunting & Doig, 1997) that identifies children’s cognitive ability within the social context of the learning. Piaget included specific methods and strategies tailored to children so that he could observe their behaviour. In mathematics education, clinical research methods are common approaches to assessing young children’s mathematical learning (Hunting & Doig, 1997; Ginsburg, 2005; Opper, 1977; Sarama & Clements, 2009; Warren et al., 2012).

A clinical interview involves many methods and strategies. They include intensively working one-on-one with an individual child, an ongoing conversation between the adult and the child and the inclusion of flexible questioning based on how the child is interacting (Ginsburg, 2005; Posner & Gertzog, 1982). Clinical interview methods highlight language as a significant component. The dialogue between the participant and the researcher supported the researcher to clarify, ask questions and pose problems during the CMTLE interview. According to Hunting and Doig (1997), the questioning should be open-ended in design, include freedom of choice in responses, maximise discussion opportunities and allow for the researcher and the student to reflect on the process.

Design of the CMTLE

For the purpose of this study, each learning experience of the CMTLE was designed to include (i) a pre-planned mathematics learning experience with an open-ended question (Nicol & Bragg, 2009; Sullivan & Lilburn, 1997) posed to students, (ii) opportunities for multiple entry points (Jorgensen et al., 2010) and (iii) appropriate physical manipulatives (concrete material or a visual stimulus) (Cooper & Warren, 2007; Lingefjärd, & Ghosh, 2016; MacDonald & Lowrie, 2011) to support the experience. Designing each learning experience to be an open-ended experience provided the opportunity for students to solve the problem in multiple ways.

In addition, each learning experience covered a range of mathematical content that drew from all strands of the Australian mathematics curriculum appropriate for this age group. For example, learning experience one allowed for the young student to apply their mathematical understanding in the following ways: estimating, two-dimensional space, estimation of half, coordinating the middle point using two dimensions and symmetry. Before implementing the task-based interviews, the following was conducted: (i) each learning experience was trialled with a group of young students; (ii) member checking was conducted with other experts in mathematics education; and (iii) the classroom teachers were consulted to ensure these learning experiences (and relevant mathematical content) had not previously occurred in mathematics lessons. Table 2 presents learning experience one including the physical manipulatives and examples of the teacher questions used when implementing the learning experiences.

Table 2 Learning experience one from the CMTLE
Full size table

The additional seven learning experiences included young students identifying strategies to count unseen objects; making connections with addition understandings; identifying taller towers with the use of different manipulatives; using manipulatives for a real world subtraction problem; identifying the amount of floor tiles required; equally halving irregular shapes and using spatial awareness to replicate an irregular shape.

The administration of the CMTLE took between 25 and 35 min for each student. The learning experiences were administered using a one-on-one clinical interview. All CMTLE interviews were video recorded to capture both the student responses and researchers questioning. One video camera was set up on a tripod focusing on the student and researcher. These videos were downloaded at the conclusion of the student interviews and were later transcribed for data analysis. In addition to this, the researcher also took notes and collected student work samples produced during the CMTLE.

Data analysis of the CMTLE interview

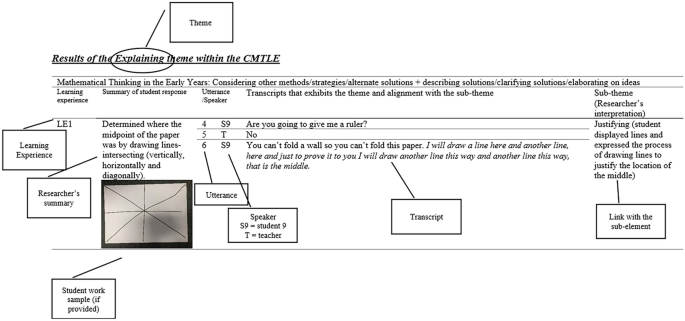
At the conclusion of the administration of the CMTLE, the high CMT students (n = 16) videos were transcribed. To analyse CMT capabilities, one researcher identified components within each high CMT student transcript that aligned with the CMT conceptual framework (see Table 1). The other researchers were consulted during the analysis phase and development of the coding systems. The CMT conceptual framework themes and sub-themes were coded for across the entire transcript, including both the student’s and researcher’s utterances. At the conclusion of the coding, all authors met to discuss the codes and examples provided. Once there was agreement, frequencies were calculated for each theme and sub-theme and provided a summary of the student responses. If a work sample was available or produced by the student, the researcher included the work sample in the table and was a part of the analysis process. Figure 1 provides an example of the collation and coding of the transcription from one student’s response for learning experience one. This is an example of the explaining theme aligned to the CMT conceptual framework.

Fig. 1
figure 1

Example of coding of transcripts using the themes and sub-themes of the CMT conceptual framework

Full size image

As depicted in Fig. 1, the first column identifies the learning experience. Column two is a summary of the student response and the inclusion of a work sample. The third column (utterance/speaker) records when the particular response occurred in the interview. For example, 4 indicates it is the fourth utterance in the interview, and T indicates that the teacher said this utterance. S9 references student 9 in the study, and T references the teacher. The transcript section that aligns with CMT is added to the next column. The final column is the researcher’s interpretation in alignment with the CMT conceptual framework sub-themes. The purpose of this process was to identify the capabilities of high CMT students.

The full analysis of the high CMT student data were coded under the following CMT conceptual framework themes and sub-themes (see Table 1).

Findings to support CMT in young students

Across the full analysis of the data pertaining to the alignment of the 16 high CMT students, there were 53 instances that evidenced critical mathematical thinking. The analysis of data identified that occurrences appeared more than once in a student’s transcript. Table 3 presents the CMT theme, the sub-theme, examples from the transcripts related to learning experience one and the frequency across all eight learning experiences.

Table 3 Frequency of CMT theme and sub-themes across the high CMT students (n = 16)
Full size table

Students exhibited responses pertaining to all five themes of the CMT conceptual framework. The most frequent theme identified in the analysis of the transcripts was explaining (20), followed by evaluating (12). The least frequent theme identified in the analysis of the transcripts was creating (6).

The descriptions that emerged from the data analysis provided a nuanced understanding of some of the sub-themes when young students are engaged in critical mathematic thinking. It was evident that there are defined CMT capabilities in young students and these align with aspects of the CMT conceptual framework that emerged from the literature. However, the in-depth data analysis found that while all five themes were present in the qualitative data, not all sub-themes were evidenced in the young students in the study. Therefore, five themes and 14 sub-themes emerged from the data analysis.

Critical mathematical thinking framework for young students

Results from this study refined the identified themes and sub-themes in the literature and provided a succinct version of a framework that begins to structure the CMT found in young students (between 5 years and 1 month to 6 years and 8 months of age) who participated in this study. The findings are related to what the 16 high CMT students displayed; however, a larger sample may allow for the expansion of the CMT conceptual framework. There were two key findings in relation to the refinement of the CMT conceptual framework.

First, the initial identified five themes were evident in the student responses; however, some were more evident than others. It appeared for these young students that explaining was the most prominent critical mathematical thinking skill displayed in their responses. The factors that may have contributed to explaining being the most prominent may include the age of the participants, the design of the tasks and the types of teacher questions posed. This was followed by evaluating. There was limited evidence of creating, interpreting, and analysing in the data.

Second, the findings from the study identified fewer sub-themes than originally presented in the CMT conceptual framework (see Fig. 2). For example, the theme in which most sub-themes were not evidenced was the theme interpreting and thus will be used as an illustrative example. The identified sub-themes drew on several researchers’ work in relation to mathematical and critical thinking (for example, Facione, 1990; Facione & Facione, 2008; Lipman, 1987; Siswono, 2010). For this particular theme, the two sub-themes that were most identified in the high CMT students (n = 16) were clarifying and estimating.

Fig. 2
figure 2

CMT Conceptual Framework for Young Students (CMTFYS)

Full size image

As only two of the eleven sub-themes were evidenced in the theme interpreting, it could, therefore, be hypothesised that this occurred for one or more of the following two reasons: (a) The other sub-themes were difficult to identify in student responses from the suite of eight CMTLE presented to these young students; (b) there is overlap between the sub-themes identified in the critical thinking literature (for example, aspects of categorising and examining form dimensions of noting relationships). Thus, in general, the definition of the sub-themes and the overlap between and across sub-themes identified in the literature requires further investigation.

Figure 2 presents the final version of the conceptual framework, now titled, Critical Mathematical Thinking Framework for Young Students (CMTFYS) with the themes and sub-themes. In addition, sub-themes within each theme are ordered from the most frequent to the least frequent.

Both sets of literature the critical thinking literature and the mathematical thinking literature are represented in the CMTFYS. The five themes that emerged from the results of this study aligned with the five themes that were identified in the literature review. The themes, interpreting, analysing and creating emerged from the critical thinking literature while evaluating and explaining emerged from both critical thinking and mathematical thinking literature.

Limitations and future directions

There are a number of potential limitations to consider from the interpretation of findings which can provide direction for future research. One limitation was that the findings in this paper focused on a small sample of young students, resulting in limited generalisations drawn from the data. However, the data provided rich descriptive information about young students’ CMT and teacher methods to exhibit CMT. As a second limitation, the young students were from similar schools in NSW. We suggest the study is repeated with more young students in various school and early learning settings to provide transferability of results. Third, the learning experiences were intended for implementation prior to the young students engaging in similar content or learning in class. It would be beneficial to ensure a repeat of the study was to occur in advance of too much school-based teaching input.

It is imperative that further research in CMT can take these factors into consideration. The findings of the study highlight the importance of the CMTFYS as a platform for teachers to support young students to exhibit CMT. It is by fully understanding CMT and the themes and sub-themes of the CMTFYS that teaching and learning practices will be modified to support young students in their mathematics learning. As the data reported in this paper is a part of a larger mixed method study, future papers will report on other key finding which includes a proposed model to support teacher questioning to exhibit young students’ CMT and how the model can influence approaches teachers use.

Conclusion

In order to address the aim of the paper, the findings are aligned to the research question, what are the CMT capabilities young students exhibit as they begin formal schooling? First, the use of the Critical Mathematical Thinking Framework for Young Students is a unique contribution to the research literature and supports the definition and conceptualisation of critical mathematical thinking for young students. Additionally, the blending of both sets of literature (critical thinking and mathematical thinking) and the refinement of themes and sub-themes supported the formation of the notion of CMT, a domain specific thinking with critical thinking. A second finding of this study suggest that a literature and data informed conceptual framework—CMTFYS is required to support teachers in identifying CMT in young students. The analysis of data and identification of findings highlight that the development and use of a conceptual framework (CMTFYS) supports the definition of CMT capabilities in young students. The definition in the CMTFYS is presented as five themes and 14 sub-themes. As discussed, there are differing views as to whether critical thinking is subject specific or standalone. A body of literature supports domain-specific knowledge as a requirement for critical thinking (Bailin, 2002), whereas Facione (1990) and Facione and Facione (2008) believe critical thinking is across all content or subject areas. The CMTFYS supports and extends on the literature that critical thinking is subject specific.

Conclusions drawn from this study confirm that CMT can be evidenced in young students. New insights are gained into CMT presented by young students in two ways. First, findings presented from this study offer a unique contribution with the development of the CMTFYS. Furthermore, the CMTFYS is specific to young students and can be considered for use in both prior to school early learning settings and formal primary school classes. Second, the data from the young students used for the refinement of the CMTFYS demonstrated sophisticated CMT. More instances of identifying such thinking from young students can shift the ways teachers plan for mathematics learning.

Based on the conclusions of this study, there are implications for curriculum, teaching and learning, and recommendations for teaching and research with the future application of CMTFYS.

A practical implication from this study is that the curriculum (both national and international e.g., Australia; Singapore; NCTM) for students in their first year of formal schooling includes the themes and sub-themes of the CMTFYS. Within an international context, the CMTFYS has potential to provide a nuanced framework to support and scaffold how young students exhibit critical mathematical thinking and how this differs to, and or aligns with, the identified mathematical processes in the curriculum (e.g., how does CMT for young students align with problem solving, reasoning and proof, communication, connections and representations as identified by NCTM). In the Australian context, this could be in the form of mathematics proficiencies (problem solving, understanding, reasoning, fluency) that are also supported through the critical thinking general capability (ACARA, 2014). It is anticipated that the CMTFYS has the potential to provide clarification of what specific mathematics proficiencies are for young students and will assist teachers in identifying CMT during mathematics learning experiences. This will provide a better understanding of how critical thinking is exhibited within the specific subject domain of mathematics.

The results from this study can enhance teachers’ knowledge about CMT. Therefore, it is recommended further understanding of CMT is required by teachers of young students. In addition, teachers can consider ways in which open-ended learning experiences can be embedded in their practice.

This study has framed a new term in mathematics educational research, critical mathematical thinking, and has evidenced how this conceptual framework can be applied to a research study with young learners. It is apparent that there is more work to be undertaken in this space with a larger sample of students from a range of contexts to continue to develop and refine or expand the conceptual framework and application of the framework across the primary school setting. Despite this, the application of the conceptual framework as a means to better understand the critical mathematical thinking capabilities for young students presents a contemporary shift in the literature that continues to support the strengths young children bring to the mathematics classroom as they begin school.