Introduction

Learning progressions (LPs) describe validated pathways of how children typically develop knowledge within a specific domain, which support pedagogical, learning design and assessment components for learning (Black et al., 2011; Clements & Sarama, 2009). These progressions have become increasingly prevalent in the fields of mathematics (see Clements & Sarama, 2009; Confrey et al., 2014b; Siemon, 2019) and science education (see Lehrer & Schauble, 2015; Steedle & Shavelson, 2009) as they offer a fine-grain map of possible learning pathways a child may experience and take throughout a particular topic. There is an opportunity to build upon this foundational research for early childhood education in ways that consider learning from multiple perspectives.

Current research on the development of LPs typically describes pathways of learning without the explicit consideration of how related skills and contexts directly or indirectly influence learning. This issue has been highlighted in recent times by Gallacher and Johnson (2019), who state that the current theoretical assumptions of LPs oversimplify the learning process. This oversimplification is due to a focus on content and less attention paid to the direct or indirect influences of learning, such as contexts, ways of reasoning and pedagogical structures. When the process of learning is oversimplified, it can undermine the use and validity of the framework for teaching, learning and assessment practices. On the other hand, by ignoring or undervaluing the context and ways young children engage with the different ideas and problems, there can be a minimal impact on the way skills are developed and applied (Gallacher & Johnson, 2019). Currently, there are many approaches for developing LPs that provide standard assumptions about the nature of learning. However, we believe that they are not entirely appropriate for early childhood education because of the child-led, play-based, emphasis in Australia underpinned by the Early Years Learning Framework (EYLF) (Department of Education, Employment and Workplace Relations [DEEWR], 2009). Thus, different viewpoints of LP are necessary to address several issues that contradict the foundations of early childhood education, such as an over-reliance on standardised and formal testing approaches (including clinical interviews), which can contribute to the oversimplification of LPs. Furthermore, Duschl (2019) argues that LP development needs to move beyond the identification and mapping of conceptual learning goals, including scientific and mathematical practices and cognitive and epistemic learning goals. Nevertheless, the emphasis on science, technology, engineering and mathematics (STEM) education as an integrated pathway for curriculum design has been said to have added another layer of complexity in the development of LP research. That is, there is the potential for epistemic clashes within and between the STEM disciplines that affect how such LPs can accommodate the cognitive, curricula, pedagogical and assessment components authentically (Cunningham & Kelly, 2017).

In response to these issues raised above, we propose the Bounded Learning Progression (BLP), which is a redefined LP architecture demonstrating the connection and influence reasoning skills have on specific domains of knowledge, bounded by the context in which learning occurs. That is, BLP are learning maps that describe possible pathways of learning which will contribute to achieving different layers of reasoning in STEM learning contexts. The BLP provides a framework that articulates the connection between conceptual learning, ways of thinking and reasoning and how key heuristics support early childhood education’s social and epistemic practices. In this paper, we describe and illustrate the BLP architecture in the context of a national early learning STEM program. The BLP is designed to exemplify the interactions between conceptual knowledge and other cognitive capabilities and the role pedagogy plays more broadly, providing a complete account of learning in early childhood contexts (specifically 4–8-year-old contexts). We will conclude by arguing that this framework can be used universally in early childhood education for empirically describing the authentic conditions in which learning develops in any domain.

Learning progressions: current theoretical perspectives

The idea of what constitutes a learning progression (LP) (also referred to as learning trajectories) has its roots within developmental psychology, with the underlying premise that children are not miniature or incomplete adults; instead, they are capable and confident beings that continuously build their understanding of the world through their interactions and experiences in a range of everyday contexts (Confrey, 2019). The contexts and interactions that children experience through formal and informal educational opportunities are as individual as the children themselves, yet this is not always reflected in the theoretical framework guiding the development of such progressions. For example, Lehrer and Schauble (2015) argue that:

“a vital goal of LP research is to reconceive subject matter domains so that what is taught and how it is sequenced become a central focus of the research, rather than being taken for granted as starting points” (p. 434).

Thus, there is tension between the formal curricula and learning frameworks provided by educational bodies and researchers (Duschl et al., 2011; Fonger et al., 2018) and how children develop their conceptual understanding, skills and practices in their everyday worlds.

In Australia’s pre-school and early years settings, a significant level of flexibility and agency is provided to and indeed required from educators to develop nuanced educational experiences for children that demonstrate pedagogical responsiveness and a child-centred approach to learning (Grieshaber, 2018). However, educators are restrained by a prescribed curriculum in the more formal school context, which often lacks a fine-grained understanding of how children’s learning and ideas evolve in each topic within a discipline area (Lobato & Walters, 2017). This issue has been a catalyst for our research into LPs to help uncover how discipline-based conceptual ideas evolve in a range of different contexts across the early years of education. In this case, our research on LPs takes a different perspective from traditional models. We specifically explore how LPs can encapsulate early childhood development from pre-school into the early years of schooling with an explicit focus on context, pedagogy epistemic views of cognition. These views align with early childhood theoretical perspectives of learning—namely sociocultural theory (e.g. Bronfenbrenner & Morris, 2006; Vygotsky, 1978). There are many advocates for an LP approach to curriculum design that offers authentic, conceptual and research-driven approaches to educating children in place of traditional standards and curricular sequences (see Battista, 2011; Clements & Sarama, 2004, 2017/2019, 2021; Confrey et al., 2014a). However, we see this foundational work as an opportunity to extend the theoretical positioning of LPs further and inform the practical implementation specifically for early childhood education.

Examining current learning progression architectures

Learning Progression and learning trajectory are used synonymously and separately in the research literature, with differences, especially evident between mathematics and science education disciplines. First termed by Simon (1995) as a hypothetical learning trajectory (HLT) for mathematics education, a HLT was designed as a teaching construct, whereby the teacher hypothesised what the child currently knew and could do, and what pathway they would need conceptually to deepen the knowledge. They do not assume that all children would follow the same pathway in learning development. However, an issue in the development of such trajectories is determining how variations in instruction and opportunity may affect children’s learning development (Battista, 2011). Conversely, learning progressions are often viewed as long-term descriptions that document children’s movement through benchmarks that are predetermined as a result of researchers’ rational analysis of particular content (Ellis et al., 2014; Battista, 2011; Lobato & Walters, 2017). They too are not designed to be depicted as fixed or linear pathways; however, in practice, many are designed and or used in such a way (Gallacher & Johnson, 2019). Our goal in this paper is not to provide an argument for determining the differences between the two. In Australia, there is a familiarity with the term progression over trajectory; thus, we use progressions for the remainder of the paper.

A range of theoretical and methodological approaches are used to construct LPs, depending on the intention or audience, discipline, concept focus and researchers’ perspectives. For example, Lobato and Walters (2017) describe seven approaches for developing learning progressions; however, in our analysis of these methodological assumptions, three approaches are most common in the development of LP in early childhood mathematics education.

The first approach is a cognitive-level, or scheme-based, approach. Using this approach, several researchers have focused on articulating disciplinary-specific learning (e.g. Barrett et al., 2009; Battista, 2004; Clements & Sarama, 2009). A cognitive level LP is predominantly used for diagnostic assessment purposes, which can include identifying and classifying partially productive understanding of concepts, generally within broad mathematics topics such as “geometry” or “number” (Lobato & Walters, 2017, Clements & Sarama, 2004). Cognitive level LPs generally describe discipline-specific ways of reasoning about a topic, irrespective of curriculum, and focus on understanding and reacting to children’s current cognitive structures (Battista, 2011). They include a beginning “level” or anchoring starting point and end in a deeper, more sophisticated benchmark of a learning goal. The most common method for developing a cognitive level LP involves cross-sectional, clinical interviews over multiple ages, which become “compilations of empirical observations of the thinking of many students” (Battista, 2004, p. 187). However, a limitation of this type of LP methodology is that it does not examine the influence of innovative and intentional teaching opportunities and does not incorporate learning construction in the “messiness” of everyday, play-based learning, experiences that are vital to early years’ education. Consequently, while utilising this approach may enable the mapping of cognitive patterns in children’s thinking to understand the conceptual structures for achieving a range of learning goals, this approach does not explore, or at best backgrounds, the range of possible learning mechanisms that support higher levels of thinking. This methodology does not capture the non-disciplinary reasoning, and cognitive structures children may employ to establish understanding, which we believe is vital to establishing a holistic understanding of how learning develops in the early years.

The observable strategies approach is the second most prevalent approach concerned with LPs and describing young children’s mathematical activity. This type of LPs articulates a range of behaviours and strategies that children may exhibit within learning tasks, and teachers may embed them in their pedagogy to influence and describe a child’s level of understanding (see Confrey et al., 2014b; Maloney & Confrey, 2010; Lehrer & Schauble, 2015). This type of LPs typically identifies proficiency levels in describing learning through action verbs rather than the language of mental conceptions (Lobato & Walters, 2017). This type of LPs intends to draw connections between the sophistication in children’s strategies while considering the impact variables such as task complexity, cultural context and the learning environment may have on learning. This type of learning progression can be constructed upon existing research (such as disciplinary logic/curricular coherence approaches) or it can be a product of research (Lobato & Walters, 2017). Thus, there is no prototypical method for constructing this type of LP which raises concerns regarding consistency.

Furthermore, this methodology of learning progression construction lends itself to the formal design of measures to empirically validate the LP (Confrey et al., 2014b), because knowledge states are encapsulated within the learning performances (Lobato & Walters, 2017). Therefore, play-based or child-initiated demonstrations of knowledge are not captured. The limitation of this methodological approach is that a learner can demonstrate a desirable behaviour that may be interpreted as conceptual understanding (Ellis et al., 2014) at multiple levels at the same time within a given LP, rendering the LP inconsistent with the purpose of the frameworks (see Alonzo & Steedle, 2009; Steedle & Shavelson, 2009).

The third relevant approach to developing LPs is the hypothetical learning trajectory (HLT). This approach shifts the focus from the learner per se to the learning supports, pedagogical approaches and tasks that will promote children’s development within a conceptual domain. As described above, this approach was first conceived by Simon (1995) and consists of three main elements: a learning goal; the selection of tasks that will promote children’s learning towards the identified goal; and a hypothesis about the process or path of learning a child may take (Simon & Tzur, 2004). Clements and Sarama (2004) elaborate, stating that HLT are:

“descriptions of children’s thinking and learning in a specific mathematical domain and a related, conjectured route through a set of instructional tasks designed to engender those mental processes or actions hypothesised to move children through a developmental progression of levels of thinking, created with the intent of supporting children’s achievement of specific goals in that mathematical domain” (p. 83).

HLT are commonly situated in a constructivist, socio-constructivist and/or social-cultural paradigm of learning. That is, these foregrounding theories exert a profound influence on the meaning of these progressions because they define the likely catalysts for learning development and provide a theoretical base for explaining the movement between the steps identified within the progressions (Confrey, 2019; Simon et al., 2010; Simon & Tzur, 2004). As described by Clements and Sarama (2004), HLT are powerful learning tools as they “can actually alter developmental progressions or expectations previously established by psychological studies, because it opens up new paths for learning and development” (p. 84) This is a critical feature of such an approach, in that its design and development are ongoing, iterative, context-specific, informed by the interpretivist nature of seeking information from children regarding their engagement and integration within a learning experience (Lehrer & Schauble, 2015). Thus, the power of an HLT comes from the nexus between the developmental path a child is conjectured to explore within a defined concept and the carefully selected teaching and learning experiences that are developed and selected to promote this learning (Daro et al., 2011).

There are limitations to a HLT approach identified by several researchers that explicitly relate to early childhood education. The first is recognised by Simon et al. (2010) in their description of a lack of specificity over the learning processes identified or evidenced within a HLT and how children use them intuitively to develop deeper and more sophisticated ways of knowing. Additionally, Lobato et al. (2012) argue that there is a lack of connectedness and consideration of what other learning goals and pathways for learning may have on the current HLT of focus, such as pedagogical frameworks and ways of reasoning, which we elaborate on in the forthcoming section. Similarly, the notion of mathematical practices, including the social environment, is not a central focus of this approach.

Despite the breadth of methodological approaches that have emerged within mathematics and science education over recent decades, there is an opportunity to develop a more integrated approach for developing learning progressions to suit the nature of learning within early childhood education. Foundational platforms for where and how learning develops and for whom and in what contexts the learning takes place (Lesh & Yoon, 2004) should be empirically established to better determine age-appropriate developmentally appropriate progressions (Duschl, 2019). After all, “mathematical constructs (and conceptual systems) develop along a variety of dimensions” (Lesh & Yoon, 2004, p. 207). Unfortunately, this complexity and emphasis on ways of reasoning and social practices do not appear to be a central element in the construction of many LP frameworks, which undermines the learner, the way in which learning develops and the learning possibilities and potential.

In summary, we note that the theoretical underpinnings of LPs tend to assume “descriptions of the successively more sophisticated ways of thinking about a topic that can follow one another as students learn about and investigate a topic over a broad span of time” (National Research Council [NRC], 2007, p. 214). Furthermore, several researchers describe overarching characteristics that describe what constitutes a LP (see Confrey et al., 2019a, b; Seah & Horn, 2019; Siemon, 2019). These characteristics include that they are founded on empirical research regarding children’s behaviours, actions and thinking processes that situate learning from constructivist and sociocultural perspectives; they are dynamic in the sense that they represent predicted pathways of how and when children may develop a concept or big idea which includes a description of the challenges and landmarks or partial knowledge points that describe the learning. Finally, instruction is key to developing progress, and therefore, LPs are always domain-specific. Yet, we believe that this last point has the greatest potential for reimagining LP for early childhood contexts, to move from a disciplinary or content perspective towards a framework that foregrounds the role of practices, context, pedagogical and epistemological frameworks.

Although we take inspiration from the work above and acknowledge the contribution these and other large-scale research have made to mathematics and science education, we maintain that the current LP frameworks that articulate the role of situated contexts, as well as the epistemic and social practices within play-based settings, are undeveloped for early childhood education. Therefore, we propose that a Bounded Learning Progressions architecture extends the theoretical foundations of current learning progressions by actively addressing limitations current frameworks present for capturing learning authentically in early childhood education.

Bounded Learning Progression architecture

The Bounded Learning Progression (BLP) was derived from work undertaken within a national Early Learning, Science, Technology, Engineering and Mathematics (STEM) program in Australia (ELSA). ELSA is a play-based learning program for children aged between 4 and 8 years, to explore science, technology, engineering and Mathematics (STEM), encompassing both digital and non-digital learning opportunities (see Early Learning STEM Australia Homepage, https://elsa.edu.au/, last accessed 2022/05/30 for details).

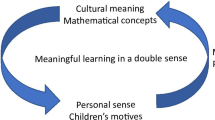
BLP have been developed to describe an architecture that represents the connection and influence that overarching reasoning constructs and practices have on learning in specific domains, bounded by the context in which learning develops (Cutting & Lowrie, 2019). The fundamental philosophy driving the development of BLP is that learning in early childhood is play-based, child-led and supported by responsive and intentional engagement by educators and teachers (Lowrie, 2021). The architecture of BLP is presented in Fig. 1 and comprises interconnected elements, which will be exemplified throughout this paper.

Fig. 1
figure 1

Bounded Learning Progression architecture

Full size image

The architecture is represented in a layered manner rather than a hierarchical order. LPs are constructed and re-iterated from a viewpoint that STEM should not be described as discrete disciplines in the early years. Instead, STEM should be considered within a practices framework that is translational in nature (Lowrie et al., 2018). The content bound traditions of science, technology, engineering and mathematics are replaced by a broader view of learning, which is especially appealing in the early years of learning due to the play-based nature of early childhood education. Our view of STEM draws attention to the numeracy contexts and mathematical ideas young children intuitively explore in both structured and unstructured learning contexts. As STEM is not defined by a curriculum, the STEM practices (Lowrie et al., 2018) (such as patterning, decoding, encoding, problem posing and solving) are mathematical in nature, and thus drive the conceptual development for learning. Therefore, individualised learning is not captured solely by content knowledge but by the reasoning skills that contribute most to STEM practice development, namely spatial reasoning and logical reasoning. The architecture acknowledges the importance of concept development (namely STEM concepts) and the particular pedagogical underpinnings (for us, the Experience–Represent–Apply [ERA] heuristic) that work together in capturing children’s learning in early-years settings. Each layer of the BLP will be unpacked throughout this paper.

Spatial and logical reasoning: the foundations of thinking as a practice

Spatial reasoning and logical reasoning provide the twin overarching reasoning domains underpinning the entire ELSA program because they are deeply embedded in early childhood learning and education. In addition, spatial and logical reasoning provide vehicles for the way in which children reason through conceptual ideas and make meaningful connections for themselves, thus helps to address the epistemic dilemmas within and between the STEM disciplines, as discussed in the “Learning progressions: current theoretical perspectives” section.

Spatial reasoning has been established as a critical skill for everyday tasks such as learning, training and working (Uttal et al., 2013). Spatial reasoning helps us understand, appreciate and interpret our three-dimensional world, including navigating our surroundings or following a diagram while building furniture (Ness et al., 2017). A large and growing body of research (e.g. Lauer & Lourenco, 2016; Margulieux, (2020); Uttal & Cohen, 2012; Wai et al., 2009) has demonstrated the link between spatial reasoning and later performance in STEM subjects at school. Spatial reasoning is also a strong predictor of a STEM career, post-formal education. In early childhood education, spatial reasoning is a fundamental “big idea” that children engage in the way they come to understand and make sense of the world. Moreover, a child’s spatial skill ability at kindergarten is a key predictor of their overall mathematical success later in school (Verdine et al., 2014), meaning that this is a critical area in children’s early learning development.

Logical reasoning is an essential part of young children’s development, and with the right experiences, children can engage in various forms of reasoning that enable them to develop arguments and construct conceptual understanding in authentic contexts (Sarama et al., 2018). The term logical reasoning describes the ability to draw conclusions based on a set of given premises (Morsanyi & Szücs, 2014). Like spatial reasoning, logical reasoning is not a single construct but a range of processes used in thinking and problem solving, dealing with the principles and criteria of validity of inference through a systematic approach (Johnson-Laird, 1999). The mental recognition of cause-and-effect relationships is called “reasoning”. It may involve predicting an event from an observed cause or the inference of a cause from an observed event. Logical reasoning derives a logical inference from a hypothesis to reasoning and is commonly classified into two forms—deductive and inductive reasoning (Evans, 2002). By definition, deductive reasoning yields a valid conclusion, which must be true if its premises are true (Johnson-Laird, 1999). For example, an argument using the rule of modus ponens would be as follows: if p then q, p; therefore q. In an early childhood context, this could be as follows: All parrots can fly. Fred is a parrot. Fred can fly. The argument could also be described by the modus tollens: if p, then q, not q; therefore, not p (Goel, 2007; Markovits et al., 2002). In this context, the argument could be as follows: All parrots can fly. Bert is a horse. Bert cannot fly.

Inductive reasoning facilitates problem-solving and expertise in learning and performance of STEM-related domains; therefore, it is an essential way of reasoning for young children to develop as they construct knowledge about the world they live in (Harverty et al., 2000). Phye (1997) identified a set of cognitive operations and processes that are foundational to inductive reasoning. They are illustrated in Table 1.

Table 1 Cognitive operations and processes that underpin indictive reasoning (adapted from Phye, 1997)
Full size table

The ELSA program provides opportunities to develop logical reasoning in mathematical contexts. Spatial reasoning and logical reasoning provide diverse engagement with STEM, without specific recourse to content. That is, in a play-based setting, children’s ways of reasoning are the foundation for building conceptual understanding.

Moreover, the sophistication of the children’s reasoning is also examined, which will be elaborated later in this paper.

STEM practices: learning beyond discipline boundaries

BLP are anchored by a STEM practice approach to mathematical learning (Lowrie et al., 2018), represented in the centre of our framework. The STEM practice approach proposes that learning is deeply bound to the context in which it is developing, enabling mathematical learning (for example) to focus on a learner’s context, cultural needs and surroundings and, therefore, developed in authentic and meaningful ways (Lowrie, 2021). This element emphasises the ideas, methods and values shared across the STEM disciplines, such as finding and validating evidence, thinking critically and persistence as examples (Lowrie, 2021). The STEM practice principles behind the development of LPs and learning design more broadly provide a focused approach to fostering knowledge and skills based on what contexts the child finds engaging and how educators can extend this (Lowrie, 2021). This approach addresses the previous concerns raised above about oversimplifying how children develop conceptual understanding, how children reason and engage in the learning process and how this is captured within an LP framework.

Conceptual development rather than content knowledge

We adapted Lithner’s (2008) framework for mathematical reasoning when constructing BLP to help determine the level of sophistication a child is demonstrating and provide a diagnostic map for how interrelated experiences and activities can assist the child in moving to the next level of understanding. This framework has been adopted in various studies, including those situated in pre-school settings (see Sumpter, 2016; Sumpter & Hedefalk, 2018). Moreover, this framework provides a sound methodological lens to explore the foundations of learning through the development of STEM practices and how they are used in play-based, early childhood learning environments. We categorise three phases of learning: reasoning as an object, reasoning as a process and reasoning as a concept that apply to mathematical concepts and STEM-based learning more broadly.

Reasoning as an object considers the objects (within an activity or learning experience) as fundamental entities. They are considered the “thing” that one is doing something with (Lithner, 2008; Sumpter, 2016). Objects can be numbers or quantities, or concrete materials such as blocks, shapes figures and pictures a child is ordering to develop early seriation ideas. This initial form of reasoning is typically evident in the form of comparing, classifying and analysing specific objects to notice similarities and differences between the individual objects, their attributes and orientation or position. It can also include disembedding, which is isolating and attending to one aspect of a context or scene (Newcombe & Shipley, 2015) and is a process that is deeply connected to spatial reasoning constructs (such as spatial visualisation). Furthermore, this phase situates the conceptual learning within the STEM practices of decoding and encoding, processing information, designing and building (as an example). Logical reasoning may also provide the foundation for reasoning with conceptual ideas at this level, whereby trial and error and intuition are evident through children questioning, imagining and utilising creative practices about the objects and immediate contexts in which they are exploring.

Reasoning as a process considers the process(es) applied to an object or context, with a sequence of these changes being a procedure (Lithner, 2008; Sumpter, 2016). This process could be in the form of the child looking at a range of possible processes, steps and strategies to be considered and trialling and applying them in various contexts to achieve the desired outcome. Reasoning as a process also demonstrates an understanding of the relationship between the information explored the objects of concern and the processes applied to these objects. Cause and effect and conditional reasoning are typically emergent in this phase, although not necessarily with a secure understanding. Newcombe and Shipley’s (2015) identification of penetrative thinking, mental transformation and sequential thinking are also illustrative of this level of reasoning.

Reasoning as a concept is where children apply mathematical concepts built from a deep understanding of the interactions between the objects, their transformations (or processes performed) and their properties (Lithner, 2008; Sumpter, 2016). This phase includes compositional reasoning, which is evident when the learner can represent functions and combine them without explicit instruction—hypothesising the outcome of the composition (Piantadosi & Aslin, 2016) with the provision of clear conclusions and the ability to form generalisations about the overarching concept (Sumpter, 2016). Although this is not an exhaustive description of all the learning examples that exemplify this level of thinking and working, its underlying foundations are the demonstration of conceptual development and the ability to apply systematic and robust spatial reasoning and logical reasoning in a range of different contexts.

An important element to the three phases of sophistication for reasoning is that they should be considered, somewhat paradoxically, as both hierarchical and cyclical in nature. That is, there is a hierarchical shift from simple to complex levels of reasoning. However, the three phases are highly cyclical in that the construction of complex and sophisticated thinking within reasoning through the concept phase affords new possibilities and provocations for thinking about different objects to start a new cycle of reasoning in related and unrelated domains.

Pedagogy is influential: experience–represent–apply heuristic

BLP are intended to support teachers and educators to develop child-led learning pathways, based on the foundation of STEM practices that deeply enhance the disciplinary perspectives of mathematical development. As described earlier, current LP frameworks typically include an instructional element to the design and assessment components of the LPs itself. However, this is typically task-driven as opposed to a pedagogical and theoretical framework emphasis on responding to the child’s learning needs. This component involves a deep shift in understanding and application of how learning is supported and conceptual development promoted; therefore, the BLP encompasses a heuristic of experience, represent and apply (ERA) (Lowrie & Larkin, 2020).

The ERA heuristic is an important element shaping the development of the BLP as it provides teachers with the pedagogical framework to support learning underpinned by STEM practices (see Fig. 2).

Fig. 2
figure 2

The experience–represent–apply heuristic

Full size image

Experience

This phase is intended to draw on the knowledge, skills and ways of reasoning the children bring to the learning experiences. Children’s lived experiences are used as the foundation for concept development through social engagement and language. It is here that educators are able to draw on children’s existing skills and knowledge to engage with mathematical content and STEM more broadly.

Represent

The represent phase is an integral part of the learning development. Through a focus on STEM practices, children explore concepts and a range of methods that enable them to represent their ideas and knowledge. Included in the context of the ELSA program are digital representations whereby children can play a variety of digital games to engage with and represent STEM concepts. These representations will include creating images, interpreting pictures, visualising and using symbols, which utilises both bespoke digital resources and non-digital representations.

Apply

Children build on their learning from the on-app activities through a range of off-app learning experiences, guided by their educators and their families. In this phase, children are encouraged to seek out new and unfamiliar contexts to apply and extend their knowledge within their structured learning environments (such as pre-school and in school environments) and at home. The BLPs are designed to reflect these pedagogical and conceptual authenticity elements within child-centred play-based learning experiences.

Lowrie and Larkin (2020) explain that the heuristic provides opportunities for children to experience a concept first. By way of example, developing understandings could initially encourage children to stand in order from tallest to shortest. This concept is then represented through a digital experience in a play-based format. In this case, the on-app (R) activities scaffold the children to order objects based on seriation, including the chronological ordering of events based on time, where they play with one of the four ELSA digital characters to order a series of pictures in chronological order. The digital experience is then followed with opportunities to apply the idea to the children’s own context. They then apply what they have learned to activities off-app. Here, children can be encouraged to establish play scenarios where they can order two sets of objects (such as toys) based on a chosen attribute, such as length. The children may arrange the toys in order of length and then match them to strips of cloth of similar length, used as blankets for the toys to sleep on (Lowrie & Larkin, 2020).

Our architecture considers opportunity and context as part of a refined understanding of how children progress through learning milestones, and therefore, formative assessment is a critical component within the BLP. We believe that this heuristic, along with the conceptual framework underpinning knowledge development in the “Conceptual development rather than content knowledge” section, supports teachers and educators in identifying and promoting authentic learning opportunities in the early years of education—a tension noted in the rationale for this theoretical discussion.

Assessing progress: the role of progress indicators and “I Can” statements

Elsewhere, it has been argued that “a significant challenge … for all of us who investigate curriculum in the early years—is the issue of assessing a program’s efficacy while not relying on standardized assessment tools” (Lowrie, 2021, p. 3).

The experience and apply phases of the heuristic require formative assessment by the teacher (educator). However, the collation of assessment data can be autonomously collated on the digital tools in real time, while being considered in more holistic and contextual ways.

Similarly, digital platforms, such as the one developed for the ELSA program, can help capture learning in a more authentic and naturalistic manner. Rather than developing assessment materials that are used to indicate the level of a child’s understanding within a conceptual domain that requires individualised, interview-based assessment outside of the play-based environment, a sophisticated suite of learning analytics that records children’s individual achievement seamlessly has been developed. This data is captured by the digital tools a child engages with through intentional learning as well as during their play through the affordance of user-generated content (UGC) (see Lowrie & Larkin, (2020) for more information). Unlike other successful web-based applications for capturing real-time student data through digital assessments that are aligned to LP (see Confrey et al., 2019a, b), the data in ELSA are captured as the children engage with, and play in, the program’s learning structure which provides a more authentic representation of the child’s development. Learning and engagement are both captured by the software instantaneously, formatively and diagnostically, and in nuanced ways not possible with a battery of standardised tests. To this point, teachers can use real-time data to more effectively propose or develop learning opportunities that accommodate individual differences and diverse learning environments.

As the children play the digital games or create UGC, their engagement is recorded and presented to the educators as a series of formative “I can” statements in a separate educator app. These statements indicate what each child achieved, including the duration of their engagement and whether they needed to access the digital hints embedded in the games. Examples of different levels of “I can” statements are as follows: With help, I can sort by shape; I can make a deduction based on multiple pieces of evidence.

The “I can” statements provide a basis for constructing the BLP, which informs the development of progress indicators (PI). The PI encapsulates how the STEM practices, spatial and logical reasoning enable and influence the development of conceptual understanding and helps capture these connections in the form of a learning progression within a big idea or conceptual focus (see Fig. 3).

Fig. 3
figure 3

A representation of the connected architecture of the BLP content

Full size image

The progress indicators (PI) describe the likely pathways and levels of knowing a child exhibits when developing their understanding of a specific concept developed and represented based on the large-scale data captured by the learning management system. Each PI describes what that step in the BLP looks like in practice. Each PI describes the types of reasoning through the concepts within a conceptual domain and offers clear connections to the skills and ways of reasoning other conceptual contexts offer in the development of learning.

Each PI therefore provides the following information (see Fig. 4).

Fig. 4
figure 4

Breakdown of a progress indicator

Full size image

The analytics are captured “on App” typically during the representation phase of the ERA loop, and also the “I Can” statements that can be observed and identified by the educator during the suggested experience and apply activities. What is innovative about the structure and affordances of the BLP is the connectedness that is developed between concepts based on the frequency, types of engagement and sophistication in thinking the child exhibits within structured and unstructured learning contexts. Thus, where appropriate, the progress indicators for each BLP will have links to where that specific set of knowledge and skills can be enhanced, supported and evidenced in other learning experiences across the STEM domain (see Fig. 5).

Fig. 5
figure 5

Connections between progress indicators and conceptual knowledge

Full size image

The BLP depicted in Fig. 5 is an example of the structure and interconnectedness of learning created within the ELSA program. In this example, the STEM practice of decoding is the focus of the BLP. The first two progress indicators have been provided in the BLP (in this example), which indicate the start of a child’s reasoning capabilities for decoding and the connection the PI has in relation to pattern and relationships concepts. The example PI indicated here are accompanied by a description of what learning and reasoning at this level may look like in practice. Notably, there are connections to other relevant BLP and ERA learning experiences that likely will, in different ways, enhance and develop this child’s understanding of the concept of decoding. For example, a child who is demonstrating they are a “Representation Sense” in the above BLP likely means that they have an awareness of the role pictorial representations play in communicating meaning (including a procedure or sequence) but may not be able to describe all the attributes of the representations or apply this knowledge consistently. This may mean that they are able to decode a simple, three step, pictorial-based instructions that require mental rotation or spatial visualisation. This PI is developed and supported in the empirical data we can collect in the child’s on-app engagement; we know empirically which activities or sequences are completed more accurately than others when comparing large datasets of learners. The PI and “I Can” statements also relate to the child recognising that the symbolic representations in activity 4 on this app represent different sounds for different instruments. However, the child at this level may not be able to apply this understanding systematically or purposefully other than by trial and error to make music. To encourage this child’s success in developing decoding skills and understanding the meaning of pictorial and symbolic representations, the educator may also refer the child to other on-app or off-app experiences. Some examples may include children decoding pictorial sequences to recreate a story and activity 2 where they can practice decoding pictorial representations of familiar and unfamiliar food items to determine different attributes in sorting their lunch boxes, thus assisting the child to move to the next progress indicator (level) within the BLP.

This architecture allows for the revision of the BLP as more empirical learning evidence is collected, for example, how children are demonstrating their knowledge through their engagement in STEM practices and the application of these practices in the performance tasks provided as well as how they apply these practices in their child-led, mathematical play. In addition, this approach allows for specific conceptual aims and learning goals to be explored within and beyond the program. The tasks and learning experiences are not simply stimuli for responses but involve setting up specific conditions for learner engagement and teacher participation that is child-initiated, to promote and respond with pedagogical agility to learners activity (Confrey, 2019). Thus, the digital activities, teaching suggestions and off-app learning experiences provided are designed for two purposes. The first is to introduce and allow learners to explore conceptual learning within spatial reasoning and logical reasoning domains through deep and purposeful engagement with STEM practices. The second is to provide contexts that support children in relating STEM concepts to their experience and background and applying this new knowledge in meaningful ways.

Conceptualising the bounded learning progression

Understanding how and when children construct and demonstrate learning milestones is a critical yet challenging task in the early years of education. Currently, traditional LP approaches do not adequately consider the complexities of learning in this age group. Therefore, too often, LPs that have been developed to articulate young children’s mathematical activity are content-focused and do not acknowledge the intuitive and nuanced ways in which children construct understandings within and between concepts and contexts. In response to this issue, the Bounded Learning Progression offers an extended and authentic contribution to the theoretical foundations of what current LPs offer for the early years of education. That is a framework that contextualises learning within play-based programs that include real-time insights into children’s thinking. This is essential in the early years since development progress occurs in more nuanced ways than within interview or task-based assessment and learning progress can be captured in ways that are not limited to hierarchical signposting or formal assessments—whether digital or not. Although traditional forms of summative assessment have a place in capturing learning, we believe that it is not an appropriate base for describing or capturing young children’s ways of thinking and working mathematically.

We believe that the BLP enables the identification and monitoring of the reasoning skills and thinking processes children intuitive engage with and construct in the context of play-based learning supports a balanced understanding of learning in the early years. This is because learning is considered from multiple perspectives, including a basis for how STEM practices and spatial and logical reasoning provide the foundation for conceptual exploration of mathematics and STEM. It supports thinking about how STEM connects to the real world, which is not based on disciplinary content, but through the diverse use of the sayings, doings and relations of STEM (Lowrie et al., 2018).

The intention and foundation of our BLP are that they are focused, conjectured pathways of knowledge construction of a range of STEM concepts that manifest within spatial reasoning and logical reasoning through the engagement in STEM practices (Lowrie et al., 2018) and the ERA framework (Lowrie & Larkin, 2020). Furthermore, the BLP considers learning holistically by situating conceptual development within boundaries that consider context, pedagogy and epistemic views of cognition that are aligned with early childhood theoretical perspective of learning. The ERA heuristic enables the deep exploration of conceptual understanding to develop intuitively through play and be extended upon through intentional teaching resources that promote deeper levels of thinking and reasoning.

Conclusion

This paper describes a theoretical approach to the development of learning progressions that aligns well to early childhood’s play-based nature and the intentional teaching approach espoused in the Early Years Learning Framework (EYLF) (DEEWR, 2009). Most current forms of learning progressions describe pathways within a learning area or topic, from least sophisticated to most sophisticated levels of skills and understanding, without the consideration of how related progressions, directly or indirectly, (may) enhance or influence learning in different ways. The bounded approach to developing learning progressions provides a mechanism for capturing learning in more dynamic, holistic and authentic ways. Consequently, we define BLP as learning maps that describe the possible pathways of learning, which will contribute to achieving different layers of reasoning through the identified STEM concepts. The BLP is designed to authentically exemplify the interactions between mathematical content and other cognitive capabilities (such as spatial and logical reasoning), providing a more complete account of learning as it considers how such influences and enhances the mathematical thinking within the learning context.

We propose that such Bounded Learning Progressions need to be considered in developing future models, where it can be acknowledged that learning occurs both within and beyond intentional teaching opportunities. Thus, the BLP architecture provides a hybrid approach to the current approaches to capturing learning, which provides a more authentic and realistic representation of learning for early childhood education.