Skip to main content
SpringerLink
Log in

Axi-Symmetric Deformation in Generalized Thermoelasticity with Two Temperatures

  • Research Article - Mathematics
  • Published:
Arabian Journal for Science and Engineering Aims and scope Submit manuscript

Abstract

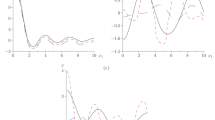
The disturbance due to normal force and thermal source in a homogeneous, isotropic generalized thermoelastic medium with two temperatures for the axi-symmetric problem in the context of generalized theories [Lord and Shulman (L-S) theory and Green–Lindsay (G-L) theory] are obtained by applying the Laplace and Hankel transforms. To get the solution in physical form, a numerical inversion technique has been applied. The components of stress, conductive temperature \({\phi}\) and temperature distribution θ are computed numerically and illustrated graphically to compare the results between the two temperature models for L-S and G-L as well as for classical one temperature theory of thermoelasticity. Some special cases are also deduced from the present problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Boley M.: Thermoelastic and irreversible thermo dynamics. J. Appl. Phys. 27, 240–253 (1956)

    Article  MathSciNet  Google Scholar 

  2. Chen P.J., Gurtin M.E.: On a theory of heat conduction involving two temperatures. ZAMP 19, 614–627 (1968)

    Article  MATH  Google Scholar 

  3. Chen P.J., Gurtin M.E., Willams W.O.: On the thermodynamics of non-simple Elastic material with two temperature. Z. Angew Math. Phys. 20, 107–112 (1969)

    Article  MATH  Google Scholar 

  4. Dhaliwal, R.S.; Singh, A.: Dynamic coupled thermoelasticity, p. 726. Hindustan Publisher Corp, New Delhi (1980)

  5. Green A.E., Lindsay K.A.: Thermoelasticity. J. Elast. 2, 1–7 (1972)

    Article  MATH  Google Scholar 

  6. Kumar R., Pratap G.: Axi-symmetric free vibration of infinite micropolar thermoelastic plate. AMM 28, 364–383 (2007)

    Google Scholar 

  7. Kumar R., Singh R., Chadha T.K.: Axi-symmetric problem in microstretch elastic solid. Indian J. Math. 44, 147–164 (2002)

    MathSciNet  MATH  Google Scholar 

  8. Lord H.W., Shulman Y.: A Generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15, 299–309 (1967)

    Article  MATH  Google Scholar 

  9. Press W.H., Teukolshy S.A., Vellerling W.T. et al.: Numerical Recipes in FORTRAN, 2nd edn. Cambridge University Press, Cambridge (1986)

    Google Scholar 

  10. Quintanilla R.: On existence, structural stability, convergence and spatial behaviour in thermoelastic with two temperature. Acta Mech. 168, 161–173 (2004)

    Article  Google Scholar 

  11. Quintanilla R.: Exponential stability and uniqueness in thermoelasticity with two temperature. Ser. A Math. Anal. 11, 57–68 (2004)

    MathSciNet  MATH  Google Scholar 

  12. Sherief H.H., Saleh H.: A half-space problem in the theory of generalized thermoelastic diffusion. Int. J. Solids Struct. 42, 4484–4493 (2005)

    Article  MATH  Google Scholar 

  13. Warren W.E., Chen P.J.: Wave propagation in the two temperature theory of thermoelasticity. Acta Mech. 16, 21–23 (1973)

    Article  MATH  Google Scholar 

  14. Youssef, H.M.: Theory of two temperature generalized thermoelastic. IMA J. Appl. Math. 1–8 (2005)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, C.D.L. University, Sirsa, India

    Aseem Miglani

  2. Department of Mathematics, M.M.E.C. Maharishi Markandeshwar University, Mullana (Ambala), India

    Sachin Kaushal

Authors
  1. Aseem Miglani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sachin Kaushal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sachin Kaushal.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Miglani, A., Kaushal, S. Axi-Symmetric Deformation in Generalized Thermoelasticity with Two Temperatures. Arab J Sci Eng 36, 1581–1595 (2011). https://doi.org/10.1007/s13369-011-0139-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13369-011-0139-4

Keywords

Mathematics Subject Classification (2010)

Search

Navigation