1 Introduction

Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR MS) [1, 2] is recognized as being a useful analytical instrument because it provides the highest broadband mass spectral resolving power and mass accuracy currently available [3, 4]. For example, in order to derive the unique elemental composition from the monoisotopic mass for masses >500 Da, one needs accuracy at the sub-ppm level or better [5, 6], which can currently only be achieved by FT-ICR MS. Although it is well known that the mass-resolving power of FT-ICR varies linearly with the applied magnetic field strength and inversely with m/z and pressure [7, 8], it is less widely appreciated that the mass-resolving power of FT-ICR can be enhanced by up to a factor of 2 by phasing the magnitude-mode spectrum into an absorption-mode spectrum [9, 10].

2 Absorption and Dispersion Spectra from Complex Spectra

A digitized time-domain ion cyclotron resonance signal will yield two frequency-domain spectra after Fourier transformation [11, 12], Re(ω) and Im(ω), which correspond to the real and imaginary parts of the complex spectrum [13]. The general relation is given below:

$$ F\left( \omega \right) = \int {F(t){e^{{ - i\omega t}}}dt = A\left( \omega \right) + iD\left( \omega \right)} $$
(1a)
$$ \phi (\omega ) = \arctan [D(\omega )/A(\omega )] $$
(1b)
$$ M(\omega ) = {[ {(A(\omega ))^2} + {(D(\omega ))^2}]^{{\frac{1}{2}}}} $$
(1c)

Here, ω = 2πf is the angular frequency, F(ω) represents the frequency domain data,while A(ω) = Re(ω) and D(ω) = Im(ω) are the absorption-mode and dispersion-mode spectra, respectively. Φ(ω) and M(ω) are the phase and magnitude-mode spectra, respectively.

In general, ions are excited to their cyclotron orbits with a phase that is generated by the frequency program of the excitation pulse, and they precess continuously until detection. If this phase function, Φ(ω), is known, F(ω) can be rotated in the complex space to align all signals along the real axis. However, this phase function has generally not been known, so the magnitude-mode spectrum has been used instead.

If the spectrum is misphased by an angle (see Fig. S1, top) Φ(ω), which is a function of frequency and time, the corrected spectrum, G(ω), can be generated by

$$ G(\omega ) = \int {F(t){e^{{i\omega t}}}{e^{{i\phi (\omega )}}}} dt = \int {F(t){e^{{i(\omega t + \phi (\omega ))}}}} dt. $$
(2)

If Φ(ω) is correct, G(ω) is aligned with the real axis of the complex space, and a clean, properly phased absorption-mode spectrum is available. Thus, the trick is to find the function Φ(ω) that encodes the phase for each signal in the entire spectrum. However, it is important to note that any peak can be perfectly phased at some Φ(ω i) between 0 and 2π, but that \( \Phi \left( {{\omega_{\rm{i}}}} \right) = \Phi \left( {{\omega_{\rm{i}}}} \right) + {2}{{\hbox{n}}_{\rm{i}}}\pi \) for any integer n i at any ω i . In order to generate the useful Φ(ω), it is necessary to find the full function, which means determining the individual values of n i and Φ(ω i ).

3 The Advantages of Absorption Mode Over Magnitude Mode

Even when the very first FT-ICR mass spectra was obtained in 1974 [14, 15], it was readily recognized that an absorption-mode spectrum provides higher resolving power than a magnitude-mode peak [16]. Also, phasing is done routinely in Fourier transform nuclear magnetic resonance (FT-NMR, see Fig. S1 of the Electronic Supplementary Material, ESM) [17, 18].

The absorption-mode spectrum is preferable to the magnitude-mode spectrum for several reasons. First, the peak width at half-maximum height is narrower than its corresponding magnitude mode by a factor of 1.4–2× (Fig. 1) [19–21]. Which means that the mass-resolving power, m/Δm(FWHM), is enhanced by the same factor. Second, because the height of a perfectly phased absorption-mode spectrum is identical to its corresponding magnitude-mode peak, increasing the resolution will not affect the signal-to-noise ratio of the peak. Other methods that are used to smooth the peak shape, like apodization [22, 23], can be accomplished only at the expense of degradation of the resolution or signal-to-noise ratio. Third, foldover peaks, also known as aliased peaks [24], which are caused by sampling at less than the Nyquist frequency, can easily be detected by their anomalous phase in an absorption-mode spectrum. By contrast, identifying foldover in a magnitude-mode spectrum requires a comparison of the frequencies of the same peak in two spectra acquired at different sampling rates. Fourth, the peaks in absorption-mode spectra have a different shape, and they are very well separated at the baseline, whereas in magnitude mode, overlaps between neighboring peaks can often result in unusual signal shapes at the bases of peaks (see below).

Fig. 1
figure 1

Typical magnitude-mode and absorption-mode Lorentzian lineshapes, corresponding to the Fourier transformation of an infinite-duration time-domain signal for a sinusoidal function

Full size image

4 Spectral Phase and Frequency-Sweep Excitation

In Fourier transform nuclear magnetic resonance (FT-NMR) [25, 26] spectroscopy, signals at all frequencies are excited near-simultaneously by a short RF pulse. This can be done because an entire FT-NMR spectrum typically covers a bandwidth of a few kilohertz on a several hundred megahertz signal [27]. Thus, in NMR, this short pulse essentially simultaneously excites all of the spins, and the phase angle can usually be represented by a linear equation that is similar to the last two terms in Eq. 3 (below), so that for NMR, A = 0 in Eq. 3 [28, 29]. Furthermore, the phase variation in FT-NMR is usually less than one cycle (<2π) across the spectrum [30, 31], so phasing becomes relatively simple for NMR: choose a peak at one end of the spectrum, vary C until the absorption-mode spectrum is equal in height to the magnitude-mode spectrum, and then vary B using the same equation for a peak at the other end of the spectrum. The peaks between the two points will then all exhibit the absorption-mode shape, as shown in Fig. S1 of the ESM [19].

$$ \Phi (\omega ) = A{\omega^2} + B\omega + C. $$
(3)

For FT-ICR, it was recently demonstrated that, because of linear frequency sweep excitation, Φ(ω) is a quadratic function [32, 33]. Recovery of the absorption-mode spectrum from the complex spectrum requires the correct phase angle function, Φ(ω); see Eq. 3.

This phase, Φ(ω), has several contributions arising from [34]: (a) a zero-order phase shift (C ≠ 0) due to phase accumulation at the beginning of excitation; (b) a linear shift (B ≠ 0) due to the time delay between excitation and detection; and (c) a quadratic phase shift (A ≠ 0) for the frequency-sweep excitation [35] or stored-waveform inverse Fourier transform (SWIFT) [36].

In FT-ICR, the frequency bandwidth is much larger than it is in FT-NMR. Ions are excited by frequency-sweep excitation [35], so the phase Φ(ω) increases quadratically with frequency (see Fig. 2), and various electronic circuit components (e.g., filters) can also introduce additional nonlinear phase variation. Moreover, Φ(ω) can vary by 2π or more over even a single nominal m/z because \( { \sin }\left[ {\Phi + {\hbox{2n}}\pi } \right] = { \sin }\left( \Phi \right) \), which is known as “phase wrapping” [13]. This effect makes it relatively difficult (compared to FT-NMR) to determine the variation of Φ(ω) with frequency across a broadband spectrum. So, strictly speaking, the phase Φ(ω) of a spectral peak can be determined only within 0–2π, so Eq. 3 should be replaced by

$$ \Phi ({\omega_i}) = A{\omega_i}^2 + B{\omega_i} + C + 2\pi {n_i}. $$
(4)

Here, 0 ≤ C ≤ 2π, and n i is the number of phase cycles for a peak at ω i . Because of this complication, FT-ICR mass spectra have generally been limited to magnitude mode. However, because any peak can be “phased” iteratively, a set of phases, Φ i , can be generated for a matched set of peaks in the frequency domain. Thus, finding the correct Φ(ω) for all values of ω i becomes a quadratic least squares fitting problem where the values of n i can take on a range of specific integer values. The range of these n i values can be readily approximated from the duration of excitation and the excite–detect delay time. It is then straightforward to iterate through the expected range of n i values, phase correct G(ω) at each iteration (as in Eq. 2), and check the absorption-mode spectrum for symmetry around peaks and/or maximize the positive signal amplitude.

Fig. 2
figure 2

Top: time-domain profiles of the excitation for frequency-sweep excitation. Middle: frequency for a continuous (upper line) or stepwise (lower line) frequency sweep. Bottom: quadratic phase accumulation for the stepwise frequency sweep

Full size image

In this paper, a broadband phase-correction method based on MATLAB (MathWorks, Natick, MA, USA) that can phase a spectrum into the absorption mode is demonstrated. The algorithm calculates the optimum value of Φ(ω) for each individual data point in the spectrum so that the entire spectrum can be simply phased into the absorption mode. This method has been tested for petroleum mixtures, proteins, and top-down MS/MS spectra from ECD (electron capture dissociation), and yields a much-improved peak shape compared with a magnitude-mode spectrum, particularly at the bases of peaks. Furthermore, many low-intensity peaks that overlap at the baseline can be resolved using this method.

5 Experimental Methods

Sample Description and Preparation

The petroleum sample is a distillate fraction from crude oil, diluted initially in dichloromethane and then diluted to 500 μg/mL in a 85:15 methanol:toluene mixture and used without additional purification. Ubiquitin (purchased from Sigma-Aldrich Chemical Co., Gillingham, UK) was diluted to 100 fmol/μL and 200 fmol/μL in a 50:50 water:methanol mixture for the molecular ion charge state distribution and 11+ ECD spectra, respectively. All solvents were HPLC grade, and obtained from Sigma-Aldrich.

Instrumentation

All spectra were recorded on a SolariX 12T FT-ICR mass spectrometer (Bruker Daltonics, Bremen, Germany) using either electrospray ionization (ESI) or atmospheric pressure photoionization (APPI). Broadband frequency sweep (chirp) excitation (92–938 kHz (m/z 2000 – 200) for petroleum and 92–1250 kHz (m/z 2000 – 150) for ubiquitin, both at a sweep rate of 125 Hz/μs) was followed by direct-mode image current detection to yield 4 M data-point (32 bit) time-domain data sets.

Theory

Figure 2 illustrates how the FT-ICR spectral phase varies quadratically with excitation frequency. To a first approximation, each ion with a particular m/z value will be excited at the instant that the excitation frequency matches its own cyclotron resonance frequency during the frequency sweep. Furthermore, it is normal to delay the onset of detection by several milliseconds, because the magnitude of the RF signal excitation V p-p is >100 V, whereas the RF signal for detection is usually at the microvolt level, and the residual “ring down” of the RF signal usually saturates the pre-amplifier for a few milliseconds. In most recent versions of the FT-ICR MS software, t delay is approximately 3 ms, and the definition of t delay has a jitter of nanoseconds at most. While stable on a scan-to-scan basis at the nanosecond scale, this value of t delay varies with different pulse sequences and different instruments (particularly from different manufacturers), and therefore must be accounted for, as it can cause difficulties when calculating the phase. The “shift theory” of Fourier analysis [37] points out that the accumulated phase between the end of excitation and the onset of detection is ωt delay, which usually exceeds 2π. The phase accumulation during the delay period will vary linearly with frequency, as represented by the last two terms in Eq. 3. The first term of Eq. 3 is related to the fact that a linear frequency sweep excitation of the form sin(ωt + at 2) (where a is the sweep rate) is also a quadratic phase program. Thus, one can model the accumulation of phase during the frequency sweep as uniformly accelerated linear motion, where the phase increases quadratically with time (similar to the linear distance traveled by an object with constant acceleration). In reality, however, for the Bruker data system, the real excitation is generated in the instrument control software as a series of single-frequency excitation events of identical length. For the examples used here, there were approximately 1500–2000 frequency steps, each of 5 μs length. Note that this algorithm instead assumes a true linear frequency shift, which is a possible source of error; although this is apparently not significant (see below).

Furthermore, it is approximated that an ion with a given m/z is instantaneously excited to its coherent cyclotron orbit when the excitation reaches the resonance frequency [38]. The phase of the ion accumulates quadratically before that point, but after that instant, the ion cyclotron phase will accumulate linearly (e.g., for an ion with an m/z value of 1000 in Fig. 2, the linear accumulation will be w 1(t 1 + t delay)). In conclusion, the total cyclotron phase will be the sum of the quadratic phase accumulation during the frequency sweep and the linear increase between the instant of excitation and the onset of detection, as shown in Eq. 3.

Computational Algorithm

The entire process of phasing the FT-ICR mass spectrum is performed within MatLab, a detailed explanation of the algorithm for the process is given in “Appendix I,” and all of the MatLab code used in the process is listed in “Appendix II.” The process can be broken down into the following steps:

  1. Step 1:

    Read the data

  2. Step 2:

    Generate the frequency basis set and calibrate the m/z domain

  3. Step 3:

    Calculate the optimal phase for a set of peaks in a narrow range of the spectrum (perhaps an isotopic distribution)

  4. Step 4:

    Phase that region of the spectrum

  5. Step 5:

    Iteratively extend the range of the phase function by progressively adding more peaks and recalculating the phase function until the function can phase correct the entire spectrum

  6. Step 6:

    Baseline correction

6 Results and Discussion

Absorption-Mode Versus Magnitude-Mode Display

As recently discussed by the Marshall group [39], petroleum samples provide a particularly good test of FT-ICR mass spectrometric performance because they have extraordinarily complex sample compositions over a wide dynamic range. Thus, broadband fast Fourier transform real and phase-corrected absorption-mode ESI FT-ICR mass spectra of crude oil at 12T are shown in Fig. 3. In this case, the mass-resolving power is increased by at least 50% for the absorption mode \( ({\hbox{m}}/\Delta {{\hbox{m}}_{{{5}0\% }}}\sim {85}0,000) \) compared to its corresponding magnitude mode \( ({\hbox{m}}/\Delta {{\hbox{m}}_{{{5}0\% }}}\sim {5}00,000) \) (Fig. 3, bottom inset). Several small, negative direction peaks in the absorption-mode spectrum (Fig. 3, bottom) are the errors that arise from the assumption of a true linear frequency shift (see Fig. 2), because the excitation is in fact generated as a series of single-frequency pulses, as mentioned before. The use of a stored-waveform inverse Fourier transform (SWIFT) [40] or a more finely grained excitation pulse series should eliminate these.

Figure 4
figure 3

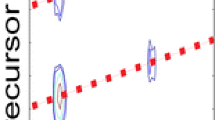
(A) Magnitude-mode ECD spectrum for the 11+ charge stage of ubiquitin, along with a close-up that shows the peak density of the raw data. (B) The absorption- (bottom) and magnitude- (top) mode spectra of the region of (A) around m/z 882. (C) The absorption- (bottom) and magnitude- (top) mode spectra of the region of (A) around m/z 1066. In both (B) and (C), the absorption-mode spectra clearly improve peak shapes and resolution without distorting the intensities. (D) The absorption- (solid) and magnitude- (dotted) mode spectra of the precursor ion isotopic distribution at m/z 779–780

Full size image

If we consider Fig. 3, it is particularly interesting to note (Fig. 3, bottom inset) that the magnitude-mode spectrum (dotted line) and the absorption-mode spectrum (solid line) have significantly different peak shapes, which lead to some unusual baseline effects that are commonly observed in FT-ICR mass spectra. Note that the distortion of the magnitude mode depends on the degree of peak overlap, the relative magnitudes of the overlapping peaks, and the signal damping rate [41], as well as the relative phase of the overlapping peaks [42]. In particular, the “tails” of the magnitude mode's Lorentzian function tend to distort the positions of neighboring smaller peaks. Because the “tails” of the dispersion-mode spectrum extend much farther than the “tails” of the pure absorption-mode spectrum, and the magnitude-mode peak is a vector summation of both, neighboring peaks must be farther apart to achieve the same degree of overlap as absorption-mode peaks. Furthermore, the deviation from this summation (see Fig. 3, inset) suggests that the absorption-mode spectrum should provide better mass accuracy than the magnitude-mode spectrum, over and above the increase in mass accuracy associated with the improved resolution.

Resolving Power

Figure 4 shows the comparison of magnitude-mode and phase-corrected absorption mode tandem mass spectra for the 11+ charge stage of ubiquitin. Again, the mass-resolving power for the absorption mode was observed to be >50% higher than that of the magnitude mode at half height, and many overlapping isotopic peaks were better resolved in the absorption mode. Also notice that the peaks are separated far better at their bases (Fig. 4D) than in magnitude mode, as in Fig. 3. As is commonly observed in unapodized FT-ICR spectra, the baseline of the magnitude-mode isotopic distribution (Fig. 4, bottom) rises and falls through the peak cluster due to the summation of the Lorentzian “tails” of the peak shape distributions. This effect is not observed in the absorption-mode spectrum, but a slight distortion of the peak shape and a negative baseline drift (due to imperfect phase correction) is observed, which can be corrected (see below). In spite of these peak shape distortions, the absorption mode still generates far sharper spectra.

Figure 5
figure 4

(A) The magnitude-mode spectrum of an oil sample. (B) The absorption-mode, phase-wrapped spectrum of petroleum (four cycles are apparent in the periodic phasing throughout the entire spectrum, indicating slight errors with the phase function shown in the inset). The labeled point (arrow) is misphased by 4π, so this frequency and phase pair are added to the fitting list with the phase adjusted by adding 4π. (C), (D) show further iterations, with more peaks added to the fitting list until the best fit (D) is obtained

Full size image

Additionally, it is reported that the peaks in a phase-corrected spectrum obtained from Fourier deconvolution will exhibit a characteristic leading effect [43]. Such asymmetry also exists in the magnitude-mode spectrum; however, the broader base of the magnitude mode largely hides this effect. The asymmetry may be caused by frequency drift [44] occurring in the time-domain transients at the early stage, perhaps due to evolution of the ion cloud geometry and concomitant space charge effects immediately following excitation. However, upon viewing the spectra shown here (Fig. 4d), it is clear that the peak asymmetry does exist but that it is not as significant as it is in the absorption-mode spectrum obtained by Fourier deconvolution. This suggests that correction by the phase function, Φ(ω), may partially modify these error sources, and investigation of the effect is still underway.

Iteration

Figure 5 illustrates the phase iteration procedure. Figure 5a is simply the magnitude-mode spectrum, but Fig. 5b shows the absorption-mode spectrum correctly phased only in a small region around m/z 450, with the rest of the spectrum periodically coming into and out of phase. The point marked by an arrow is misphased by 4π. When this frequency and phase are added to the fitting list and corrected by 2π, and the quadratic least-squares fit is recomputed, the phase function shifts slightly (see the parameters in the inset) to form Fig. 5c. Note that the periodicity of the absorption-mode spectrum has decreased in Fig. 5c,. This iteration procedure is continued until the best absorption-mode spectrum is obtained (Fig. 5d). It is clear from the small negative blips in Fig. 5d that this phase function is not perfect, which is likely due to the stepped frequency sweep excitation and imperfect centroiding of the peaks in the quadratic least-squares fitting list. However, this phase-corrected absorption-mode spectrum represents a significant improvement over the magnitude-mode spectrum in terms of resolution and peak shape.

Fig. 5
figure 5

a The magnitude-mode spectrum of an oil sample. b The absorption-mode, phase-wrapped spectrum of petroleum (four cycles are apparent in the periodic phasing throughout the entire spectrum, indicating slight errors with the phase function shown in the inset). The labeled point (arrow) is misphased by 4π, so this frequency and phase pair are added to the fitting list with the phase adjusted by adding 4π. c, d show further iterations, with more peaks added to the fitting list until the best fit (d) is obtained

Full size image

Centroiding

One significant source of error that is currently embedded in these calculations is related to the method used to calculate the peak centroid. The method currently used is the simplest method possible—defining the highest point on the peak (in magnitude mode) as the center of the peak. This method is not particularly accurate, but it improves dramatically with zero filling, so the spectra shown in Figs. 3–5 used two zero fills, thus doubling the length of time-domain data set twice. While not currently tested, it seems likely that improvements can be made to the peak centroiding algorithm, which will improve the accuracy of the Φ/ω pairs that are added to the least squares fit. Possible ways of improving centroiding algorithms include the use of a maximum likelihood peakfitting method [45], a center-of-mass calculation, a least-squares fit to a Lorentzian (or Lorentzian/sinc) function, apodization and fitting to a Gaussian function, or even use of the shifted-basis method [46]. In this work, none of these centroiding algorithms were tried, but they are an obvious next step.

Baseline Correction

The baseline in the magnitude-mode spectrum is obviously positive because the absolute value is calculated in magnitude mode. In absorption mode, the noise is a Gaussian distribution about the baseline (zero amplitude). Furthermore, the cyclotron excitation and detection range exceeds the sampling rate, which will generate a high-frequency component. Fortunately, some of these peak-shape distortions can be corrected by standard baseline correction procedures. In MatLab, this can be done automatically using a command (see “Appendices I and II”) which fits the baseline to a cubic spline and then subtracts it from the signal to flatten the baseline drift. The absorption-mode spectrum after baseline correction shows an improvement in peak shape, which would improve peak selection.

Algorithm Speed

A detailed analysis of the speed of this method is beyond the scope of this paper. Currently, this method is user interactive, requiring manual peak selection and phase assignment, so it is not very fast. However, peak selection and centroiding can be standardized and automated, as can phase determination of individual peaks, so the bulk of the algorithm could be automated. Furthermore, since the excitation pulse does not change from scan to scan, it is likely that an optimal phase function from one scan can be applied to the next scan directly. Inter-scan errors will probably arise from space-charge effects, but these are expected to be minor and can be addressed using the same iterative method as above. Given the speed of modern Fourier transform methods, it is likely that these iterations will be far faster than the data acquisition event itself, so that, in principle, iterative phasing can be done in real time.

7 Conclusion

A method of producing a broadband absorption-mode spectrum for several spectra from different samples, based on applying an iterative quadratic least squares fitting procedure, has been demonstrated. The improvement in mass resolving power and mass accuracy afforded by this new method are significant when compared with conventional magnitude-mode spectra, particularly at the bases of peaks. Additionally, peak shape is greatly improved at the baseline, except for a general negative drift, which can be corrected. This method can be applied to top-down spectra and other complex spectra in a straightforward approach.

In theory, the largest resolving power enhancement (a factor of 2) would be achieved for on-line LC FT-ICR MS, for which the time-domain acquisition period can be 1 s or less, meaning that the time-domain signal is not damped significantly. Furthermore, displaying the absorption-mode spectrum will have significant advantages when analyzing complex mass spectra, as demonstrated here for petroleum and the ECD spectrum of ubiquitin, so this approach will probably be applied to biological samples in proteomics, lipidomics and metabolomics.