Skip to main content
SpringerLink
Log in

A systematic approach to the one-mode projection of bipartite graphs

  • Original Article
  • Published:
Social Network Analysis and Mining Aims and scope Submit manuscript

Abstract

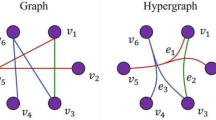
Bipartite graphs are common in many complex systems as they describe a relationship between two different kinds of actors, e.g., genes and proteins, metabolites and enzymes, authors and articles, or products and consumers. A common approach to analyze them is to build a graph between the nodes on one side depending on their relationships with nodes on the other side; this so-called one-mode projection is a crucial step for all further analysis but a systematic approach to it was lacking so far. Here, we present a systematic approach that evaluates the significance of the co-occurrence for each pair of nodes v, w, i.e., the number of common neighbors of v and w. It turns out that this can be seen as a special case of evaluating the interestingness of an association rule in data mining. Based on this connection we show that classic interestingness measures in data mining cannot be applied to evaluate most real-world product-consumer relationship data. We thus introduce generalized interestingness measures for both, one-mode projections of bipartite graphs and data mining and show their robustness and stability by example. We also provide theoretical results that show that the old method cannot even be used as an approximative method. In a last step we show that the new interestingness measures show stable and significant results that result in attractive one-mode projections of bipartite graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Notes

  1. This part reproduces parts of the conference version published with IEEE (Zweig 2010). Reproduced with permission.

  2. According to an interestingness measure called conviction.

  3. This is given under the assumption that the occurrence of M in the random graph model is normally distributed.

  4. Note that the actual number \(|{\fancyscript{G}}(L,R)|\) of graphs in \({\fancyscript{G}}(L,R)\) is not yet described by a closed formula (Greenhill and McKay 2008; Barvinok 2008).

  5. As long as this does not lead to degree 0 or degree r + 1 (l + 1) in which case nothing is done.

  6. Note that the order was chosen for displaying reasons—none of the data samples directly showed them in this order.

References

  • Abdi H (2007) The Kendall rank correlation coefficient. In: Encyclopedia of measurement and statistics. Sage, Thousand Oaks

  • Admiraal R, Handcock MS (2008) Networksis: a package to simulate bipartite graphs with fixed marginals through sequential importance sampling. J Stat Softw 24(8):1–21

    Google Scholar 

  • Agrawal R, Imielinski T, Swami A (1993) Mining association rules between sets of items in large databases. In: Proceedings of the ACM SIGMOD international conference on management of data 1993, pp 207–216

  • Alon U (2006) An introduction to systems biology: design principles of biological circuits. Chapman & Hall/CRC

  • Artzy-Randrup Y, Fleishman SJ, Ben-Tal N, Stone L (2004) Comment on “Network motifs: simple building blocks of complex networks” and “Superfamilies of evolved and designed networks”. Science 305:1107c

    Google Scholar 

  • Barvinok A (2008) Enumerateing contingency tables via random permanents. Combin Probab Comput 17(1):1–19

    Article  MATH  MathSciNet  Google Scholar 

  • Bollobás B (2001) Random graphs, 2nd edn. In: Cambridge studies in advanced mathematics, vol 73. Cambridge University Press, London

  • Brin S, Motwani R, Ullman JD, Tsur S (1997) Dynamic itemset counting and implication rules for market basket data. In: Proceedings ACM SIGMOD international conference on management of data 1997, pp 255–264

  • Brualdi RA (1980) Matrices of zeros and ones with fixed row and column vectors. Linear Algebra Appl 33:159–231

    Article  MATH  MathSciNet  Google Scholar 

  • Brualdi RA (2006) Algorithms for constructing (0,1)-matrices with prescribed row and column sum vectors. Discrete Math 306:3054–3062

    Article  MATH  MathSciNet  Google Scholar 

  • Chen Y, Diaconis P, Holmes SP, Liu JS (2005) Sequential monte carlo methods for statistical analysis of tables. J Am Stat Assoc 100(469):109–120

    Article  MATH  MathSciNet  Google Scholar 

  • Cobb GW, Chen YP (2003) An application of Markov chain Monte Carlo to community ecology. Am Math Mon 110:265–288

    Article  MATH  MathSciNet  Google Scholar 

  • Dorogovtsev SN, Mendes JF (2003) Evolution of networks. Oxford University Press

  • Gale D (1957) A theorem on flows in networks. Pac J Math 7:1073–1082

    MATH  MathSciNet  Google Scholar 

  • Gionis A, Mannila H, Mielikäinen T, Tsaparas P (2007) Assessing data mining results via swap randomization. ACM Trans Knowl Discov Data 1(3):article no. 14

    Google Scholar 

  • Girvan M, Newman ME (2002) Community structure in social and biological networks. Proc Natl Acad Sci 99:7821–7826

    Article  MATH  MathSciNet  Google Scholar 

  • Goh KI, Cusick ME, Valle D, Childs B, Vidal M, Barabási AL (2007) The human disease network. Proc Natl Acad Sci 104:8685–8690

    Article  Google Scholar 

  • Greenhill C, McKay BD (2008) Asymptotic enumeration of sparse nonnegative integer matrices with specified row and column sums. Adv Appl Math 41(4):459–481

    Article  MATH  MathSciNet  Google Scholar 

  • Hipp J, Güntzer U, Nakhaeizadeh G (2000) Algorithms for association rule mining—a general survey and comparison. SIGKDD Explor 2(2):1–58

    Article  Google Scholar 

  • Holmes RB, Jones LK (1986) On uniform generation of two-way tables with fixed margins and the conditional volume test of Diaconis and Efron. Ann Stat 24(1):64–68

    MathSciNet  Google Scholar 

  • Kendall M (1938) A new measure of rank correlation. Biometrika 30:81–89

    MATH  MathSciNet  Google Scholar 

  • Li M, Fan Y, Chen J, Gao L, Di Z, Wu J (2005) Weighted networks of scientific communication: the measurement and topological role of weight. Phys A 350:643–656

    Article  Google Scholar 

  • Ford LR, Fulkerson DR (1962) Flows in networks. Princeton University Press

  • Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002) Network motifs: Simple building blocks of complex networks. Science 298:824–827

    Article  Google Scholar 

  • Newman ME (2001a) Scientific collaboration networks I. Phys Rev E 64:016,131

    Google Scholar 

  • Newman ME (2001b) Scientific collaboration networks II: shortest paths, weighted networks, and centrality. Phys Rev E 64:016,132

    Google Scholar 

  • Newson R (2006) Efficient calculation of jackknife confidence intervals for rank statistics. J Stat Softw 15(1):1–10

    Google Scholar 

  • Newman ME, Barabási AL, Watts DJ (eds) (2006) The structure and dynamics of networks. Princeton University Press, Princeton

  • Palla G, Derényi I, Farkas I, Vicsek T (2005) Uncovering the overlapping community structure of complex networks in nature and society. Nature 435:814–818

    Article  Google Scholar 

  • Piatetsky-Shapiro G (1991) Knowledge discovery in databases. Discovery, analysis, and presentation of strong rules. AAAI/MIT Press, pp 229–248

  • Ravasz E, Somera A, Mongru D, Oltvai Z, Barabási AL (2002) Hierarchical organization of modularity in metabolic networks. Science 297:1551–1553

    Article  Google Scholar 

  • Raeder T, Chawla NV (2011) Market basket analysis with networks. Soc Netw Anal Min 1

  • Ryser H (1963) Combinatorial mathematics. In: Carus mathematical monograph, vol 14. Mathematical Association of America, Washington

  • Vázquez A, Flammini A, Maritan A, Vespignani A (2002) Modeling of protein interaction networks. ComPlexUs 1:38–44

    Google Scholar 

  • Ward JH (1963) Hierarchical grouping to optimize an objective function. J Am Stat Assoc 58:236–244

    Article  Google Scholar 

  • Wasserman S, Faust K (1999) Social network analysis—methods and applications, revised, reprinted edn. Cambridge University Press, Cambridge

  • Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world’ networks. Nature 393:440–442

    Article  Google Scholar 

  • Zhou T, Ren J, Medo M, Zhang YC (2007) Bipartite network projection and personal recommendation. Phys Rev E 76:046,115

    Google Scholar 

  • Zweig KA (2010) How to forget the second side of the story: a new method for the one-mode projection of bipartite graphs. In: Proceedings of the 2010 international conference on advances in social networks analysis and mining ASONAM 2010, pp 200–207

Download references

Author information

Authors and Affiliations

  1. Interdisciplinary Center for Scientific Computing, University of Heidelberg, Speyerer Straße 6, 69115, Heidelberg, Germany

    Katharina Anna Zweig

  2. Wilhelm-Schickard-Institute, University of Tübingen, Sand 14, 72072, Tübingen, Germany

    Michael Kaufmann

Authors
  1. Katharina Anna Zweig
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Kaufmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Katharina Anna Zweig.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zweig, K.A., Kaufmann, M. A systematic approach to the one-mode projection of bipartite graphs. Soc. Netw. Anal. Min. 1, 187–218 (2011). https://doi.org/10.1007/s13278-011-0021-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13278-011-0021-0

Keywords

Search

Navigation