Skip to main content
SpringerLink
Log in

Effect of Varying Viscosity on Two-Fluid Model of Blood Flow through Constricted Blood Vessels: A Comparative Study

  • Published:
Cardiovascular Engineering and Technology Aims and scope Submit manuscript

Abstract

Purpose

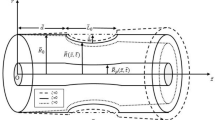
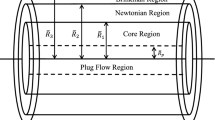
Most of the previously studied non-Newtonian blood flow models considered blood viscosity to be constant but for correct measurement of flow rate and flow resistance, the hematocrit dependent viscosity will be better as various literature suggested the variable nature of blood viscosity. Present work concerns the steady and pulsatile nature of blood flow through constricted blood vessels. Two-fluid model for blood is considered with the suspension of all the RBCs (erythrocytes) in the core region as a non-Newtonian (Herschel–Bulkley) fluid and the plasma in the cell free region near wall as a Newtonian fluid. No slip condition on the wall and radially varying viscosity has been taken.

Methods

For steady flow the analytical approach has been taken to obtain the exact solution. Regular perturbation expansion method has been used to solve the governing equations for pulsatile flow up to first order of approximation by assuming the pulsatile Reynolds number to be very small (much less than unity).

Results

Flow rate, wall shear stress and velocity profile have been graphically analyzed and compared with constant viscosity model. A noteworthy observation of the present study is that rise in viscosity index leads to decay in velocity, velocity of plug flow region, flow rate while flow resistance increases with rising viscosity index (m). The results for Power-law fluid (PL), Bingham-plastic fluid (BP), Newtonian fluid (NF) are found as special cases from this model. Like the constant viscosity model, it has been also observed that the velocity, flow rate and plug core velocity of two-fluid model are higher than the single-fluid model for variable viscosity.

Conclusions

The two-phase fluid model is more significant than the single-fluid model. Effect of viscosity parameter on various hemodynamical quantities has been obtained. It is also concluded that a rising viscosity parameter (varying nature of viscosity) significantly distinguishes the single and two-fluid models in terms of changes in blood flow resistance. The outcome of present study may leave a significant impact on analyzing blood flow through small blood vessels with constriction, where correct measurement of flow rate and flow resistance for medical treatment is very important.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11
Figure 12
Figure 13
Figure 14
Figure 15
Figure 16
Figure 17
Figure 18
Figure 19

Similar content being viewed by others

Abbreviations

\('-'\) :

The dimensional quantities

r :

Distance in radial direction

z :

Distance in axial direction

t :

Time

\(R_p\) :

Plug core (flow) radius

\(R_{p0}, R_{p1}\) :

Zeroth and first order approximation of plug core (flow) radius, respectively

\(u_H, u_N\) :

Axial velocities in core and plasma region, respectively

\(u_{H0}, u_{N0}\) :

Zeroth order approximation of axial velocity in core and plasma region, respectively

\(u_{H1}, u_{N1}\) :

First order approximation of axial velocities in core and plasma region, respectively

\(u_p\) :

Plug core velocity

\(u_{p0}, u_{p1}\) :

Zeroth and first order approximation of plug core velocity, respectively

n :

Herschel–Bulkley fluid parameter

m :

Viscosity index

K :

Constant in viscosity relation

p :

Pressure

\(p_s, q(z)\) :

Steady state pressure gradients for steady and pulsatile flow, respectively

\(Q_s, Q(z,t)\) :

Volumetric flow rate for steady and pulsatile flow, respectively

\(R_1(t, z)\) :

Radius of artery with time-dependent stenosis in core region

R(t, z):

Radius of artery with time-dependent stenosis in plama region

\(R_1(z)\) :

Radius of artery with stenosis in steady state case (core region)

R(z):

Radius of artery with stenosis in steady state case (plama region)

\(R_0\) :

Radius of normal artery

A :

Amplitude

L :

Length of the constricted blood vessel

\(\tau_H, \tau_N\) :

Shear stresses in core and plasma region, respectively

\(\tau_{H0}, \tau_{N0}\) :

Zeroth order approximation of shear stress in core and plasma region, respectively

\(\tau_{H1}, \tau_{N1}\) :

First order approximation of shear stress in core and plasma region, respectively

\(\tau_y\) :

Yield stress

\(\theta\) :

Dimensionless yield stress

\(\tau_w\) :

Wall shear stress

\(\rho_H, \rho_N\) :

Densities of blood in core and plasma region, respectively

\(\mu_H, \mu_N\) :

Constant viscosities of the blood in core and plasma region, respectively

\(\mu_H^{\prime}(r)\) :

Variable viscosity of the blood in core region

\(\rho_0\) :

The ratio of densities in plasma and core region

\(\alpha\) :

Womersley frequency parameter

\(\delta_H, \delta_N\) :

Peak height of stenosis in core and plasma region, respectively

\(\omega\) :

Angular frequency

\(\lambda_s, \lambda\) :

Flow resistance for steady and pulsatile flow, respectively

0:

Zeroth order approximation (for \(R_{p0}, u_{H0}, u_{p0}, \tau_{H0}, \tau_{N0}\))

1:

First order approximation (for \(R_{p1}, u_{H1}, u_{p1}, \tau_{H1}, \tau_{N1}\))

H :

Herschel–Bulkley fluid (for \(u_H, \tau_H, \delta_H, \rho_H\))

N :

Newtonian fluid (for \(u_N, \tau_N, \delta_N, \rho_N\))

p :

Plug flow value(for \(u_p, R_p\))

s :

Steady flow value (for \(p_s, Q_s, \lambda_s\))

w :

Value at wall (for \(\tau_w\))

y :

Value at yield stress (for \(\tau_y\))

References

  1. Ali, N., A. Zaman, M. Sajid, J. J. Nieto, and A. Torres. Unsteady non-Newtonian blood flow through a tapered overlapping stenosed catheterized vessel. Math. Biosci. 269:94–103, 2015.

    Article  MathSciNet  MATH  Google Scholar 

  2. Aroesty, J., and J. F. Gross. Pulsatile flow in small blood vessels I. Casson theory. Biorheology 9:33–42, 1972.

    Article  Google Scholar 

  3. Aroesty, J., and J. F. Gross. The mathematics of pulsatile flow in small blood vessels I. Casson theory. Microvasc. Res. 4:1–12, 1972.

    Article  Google Scholar 

  4. Bali, R., and U. Awasthi. Effect of a magnetic field on the resistance to blood flow through stenotic artery. Appl. Math. Comput. 188:1635–1641, 2007.

    MathSciNet  MATH  Google Scholar 

  5. Bugliarello, G., and J. Sevilla. Velocity distribution and other characteristics of steady and pulsatile blood flow in fine glass tube. Biorheology 7):85–107, 1970.

    Article  Google Scholar 

  6. Chakravarty, S., A. Datta, and P. K. Mandal. Effect of body acceleration on unsteady flow of blood past a time-dependent arterial stenosis. Math. Comput. Model. 24:57–74, 1996.

    Article  MATH  Google Scholar 

  7. Chaturani, P., and P. N. Kaloni. Two layered poiseuille flow model for blood flow through arteries of small diameter and arterioles. Biorheology 13:243–250, 1976.

    Article  Google Scholar 

  8. Chaturani, P., and R. Ponnalagar Samy. A study of non-Newtonian aspects of blood flow through stenosed arteries and its applications in arterial diseases. Biorheology 22:521–531, 1985.

    Article  Google Scholar 

  9. Chaturani, P., and R. Ponnalagar Samy. Pulsatile flow of a Casson fluid through stenosed arteries with application to blood flow. Biorheology 23:499–511, 1986.

    Article  Google Scholar 

  10. Dash, R. K., G. Jayaraman, and K. N. Mehta. Estimation of increased flow resistance in a narrow catheterized artery—a theoratical model. J. Biomech. 29:917–930, 1996.

    Article  Google Scholar 

  11. Elnaqeeb, T., Kh. S. Mekheimer, and F. Alghamdi. Cu-blood flow model through a catheterized mild stenotic artery with a thrombosis. Math. Biosci. 282:135–146, 2016.

    Article  MathSciNet  MATH  Google Scholar 

  12. Lih, M. M. Transport Phenomena in Medicine and Biology, 1st ed. New York: Wiley, 1975.

    Google Scholar 

  13. MacDonald, D. A. On the steady flow through modelled vascular stenoses. J. Biomech. 12:13–20, 1979.

    Article  Google Scholar 

  14. Mekheimer, Kh. S., and Y. Abd Elmaboud. Simultaneous effects of variable viscosity and thermal conductivity on peristaltic flow in a vertical asymmetric channel. Can. J. Phys. 92:1541–1555, 2014.

    Article  Google Scholar 

  15. Mekheimer, Kh. S., and M. A. El Kot. Mathematical modelling of axial flow between two eccentric cylinders: application on the injection of eccentric catheter through stenotic arteries. Int. J. Non-Linear Mech. 47:927–937, 2012.

    Article  Google Scholar 

  16. Mekheimer, Kh. S., and M. A. El Kot. Mathematical modelling of unsteady flow of a Sisko fluid through an anisotropically tapered elastic arteries with time-variant overlapping Stenosis. Appl. Math. Model. 36:5393–5407, 2012.

    Article  MathSciNet  MATH  Google Scholar 

  17. Mekheimer, Kh. S., and M. A. El Kot. Suspension model for blood flow through catheterized curved artery with time-variant overlapping stenosis. Int. J. Eng. Sci. Technol. 18:452–462, 2015.

    Article  Google Scholar 

  18. Mekheimer, Kh. S., F. Salma, and M. A. El Kot. The Unsteady flow of a Carreau fluid through inclined catheterized arteries have a balloon (angioplasty) with time-variant overlapping stenosis. Walailak J. Sci. Technol. (WJST) 12:863–883, 2015.

    Google Scholar 

  19. Misra, J. C., S. D. Adhikary, and G. C. Shit. Mathematical analysis of blood flow through an arterial segment with time-dependent stenosis. Math. Model. Anal. 13:401–412, 2008.

    Article  MathSciNet  MATH  Google Scholar 

  20. Misra, J. C., and S. K. Ghosh. Flow of Casson fluid in a narrow tube with a side branch. Int. J. Eng. Sci. 38:2045–2077, 2000.

    Article  Google Scholar 

  21. Nagarani, P., and G. Sarojamma. Effect of body acceleration on pulsatile flow of Casson fluid through a mild stenosed artery. Korea Aust. Rheol. J. 20:189–196, 2008.

    Google Scholar 

  22. Nayfeh, A. H. Introduction to Perturbation Techniques, 1st ed. New York: Wiley, 1993.

    MATH  Google Scholar 

  23. Ponalagusamy, R., and R. Tamil Selvi. A study on two-layered model (Casson–Newtonian) for blood flow through an arterial stenosis: axially variable slip velocity at the wall. J. Frankl. Inst. 348:2308–2321, 2011.

    Article  MathSciNet  MATH  Google Scholar 

  24. Ponalagusamy, R., and R. Tamil Selvi. Blood flow in stenosed arteries with radially variable viscosity, peripheral plasma layer thickness and magnetic field. Meccanica 48:2427–2438, 2013.

    Article  MathSciNet  MATH  Google Scholar 

  25. Pontrelli, G. Nonlinear problems in arterial flows. Nonlinear Anal. 47:4905-4915, 2001.

    Article  MathSciNet  MATH  Google Scholar 

  26. Rohlf, K., and G. Tenti. The role of the Womersley number in pulsatile blood flow a theoretical study of the Casson model. J. Biomech. 34:141–148, 2001.

    Article  Google Scholar 

  27. Sankar, D. S. Two-fluid nonlinear mathematical model for pulsatile blood flow through stenosed arteries. Bull. Malays. Math. Sci. Soc. 35:487–498, 2012.

    MathSciNet  MATH  Google Scholar 

  28. Sankar, D. S., and K. Hemalatha. Pulsatile flow of Herschel–Bulkley fluid through stenosed arteries—a mathematical model. Int. J. Non-Linear Mech. 41:979–990, 2006.

    Article  MATH  Google Scholar 

  29. Sankar, D. S., and K. Hemalatha. A non-Newtonian fluid flow model for blood flow through a catheterized artery—steady flow. Appl. Math. Model. 31:1847–1864, 2007.

    Article  MATH  Google Scholar 

  30. Sankar, D. S., and A. I. M. Ismail. Two-fluid mathematical models for blood flow in stenosed arteries: a comparative study. Bound. Value Probl. 2009:1–15, 2009. https://doi.org/10.1155/2009/568657.

  31. Sankar, D. S., and U. Lee. Two-phase non-linear model for the flow through stenosed blood vessels. J. Mech. Sci. Technol. 21:678–689, 2007.

    Article  Google Scholar 

  32. Sankar, D. S., and U. Lee. Mathematical modeling of pulsatile flow of non-Newtonian fluid in stenosed arteries. Commun. Nonlinear Sci. Numer. Simul. 14:2971–2981, 2009.

    Article  MATH  Google Scholar 

  33. Sankar, D. S., and U. Lee. Two-fluid Casson model for pulsatile blood flow through stenosed arteries: A theoratical model. Commun. Nonlinear Sci. Numer. Simul. 15:2086–2097, 2010.

    Article  MathSciNet  MATH  Google Scholar 

  34. Sankar, D. S., and U. Lee. FDM analysis for MHD flow of a non-Newtonian fluid for blood flow in stenosed arteries. J. Mech. Sci. Technol. 25:2573–2581, 2011.

    Article  Google Scholar 

  35. Shit, G. C., M. Roy, and A. Sinha. Mathematical modelling of blood flow through a tapered overlapping stenosed artery with variable viscosity. Appl. Bionics Biomech. 11:185–195, 2014.

    Article  Google Scholar 

  36. Shukla, J. B., R. S. Parihar, and S. P. Gupta. Effects of peripheral layer viscosity on blood flow through the artery with mild stenosis. Bull. Math. Biol. 42:797–805, 1980.

    Article  MATH  Google Scholar 

  37. Shukla, J. B., R. S. Parihar, and B. R. P. Rao. Effects of stenosis on non-Newtonian flow of the blood in an artery. Bull. Math. Biol. 42:283–294, 1980.

    Article  MATH  Google Scholar 

  38. Siddiqui S. U., N. K. Verma, S. Mishra, and R. S. Gupta. Mathematical modeling of pulsatile flow of Cassons fluid in arterial stenosis. Appl. Math. Comput. 210:1–10, 2009.

    MathSciNet  MATH  Google Scholar 

  39. Sinha, A., G. C. Shit, and P. K. Kundu. Slip effects on pulsatile flow of blood through a stenosed arterial segment under periodic body acceleration. ISRN Biomed. Eng. 2013:1–10, 2013. https://doi.org/10.1155/2013/925876.

  40. Srivastava, V. P., M. Saxena. Two-layered model of Casson fluid flow through stenotic blood vessels: applications to the cardiovascular system. J. Biomech. 27:921–928, 1994.

    Article  Google Scholar 

  41. Womersley, J. R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 127:553–563, 1955.

    Article  Google Scholar 

  42. Young, D. F. Effects of a time-dependent stenosis on flow through a tube. J. Eng. Ind. 90:248–254, 1968.

    Article  Google Scholar 

  43. Young, D. F. Fluid mechanics of arterial stenosis. J. Biomech. Eng. 101:157–175, 1979.

    Article  Google Scholar 

Download references

Acknowledgments

Authors acknowledge their sincere thank to the reviewers for their valuable suggestions and comments. Authors also acknowledge their sincere thank to SERB, New Delhi, Government of India, for providing the financial assistance grant under the research Grant SR/FTP/MS-038/2011.

Conflict of interest

Dr. Ashish Tiwari has received research grant from SERB, New Delhi, Government of India. Mr. Satyendra Singh Chauhan is getting fellowship from SERB, New Delhi, under the above research grant.

Human participants or animals

This article does not contain any studies with human participants or animals performed by any of the authors.

Author information

Authors and Affiliations

  1. Department of Mathematics, Birla Institute of Technology and Science Pilani, Pilani, Rajasthan, 333 031, India

    Ashish Tiwari & Satyendra Singh Chauhan

Authors
  1. Ashish Tiwari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Satyendra Singh Chauhan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ashish Tiwari.

Additional information

Associate Editors Ajit P. Yoganathan and David Elad oversaw the review of this article.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tiwari, A., Chauhan, S.S. Effect of Varying Viscosity on Two-Fluid Model of Blood Flow through Constricted Blood Vessels: A Comparative Study. Cardiovasc Eng Tech 10, 155–172 (2019). https://doi.org/10.1007/s13239-018-00379-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13239-018-00379-x

Keywords

Mathematics Subject Classification

Search

Navigation