A Novel Mean-Value Model of the Cardiovascular System Including a Left Ventricular Assist Device

Abstract

Time-varying elastance models (TVEMs) are often used for simulation studies of the cardiovascular system with a left ventricular assist device (LVAD). Because these models are computationally expensive, they cannot be used for long-term simulation studies. In addition, their equilibria are periodic solutions, which prevent the extraction of a linear time-invariant model that could be used e.g. for the design of a physiological controller. In the current paper, we present a new type of model to overcome these problems: the mean-value model (MVM). The MVM captures the behavior of the cardiovascular system by representative mean values that do not change within the cardiac cycle. For this purpose, each time-varying element is manually converted to its mean-value counterpart. We compare the derived MVM to a similar TVEM in two simulation experiments. In both cases, the MVM is able to fully capture the inter-cycle dynamics of the TVEM. We hope that the new MVM will become a useful tool for researchers working on physiological control algorithms. This paper provides a plant model that enables for the first time the use of tools from classical control theory in the field of physiological LVAD control.

Appendix

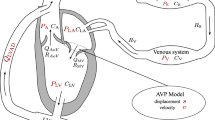
Figure 1a shows the electrical analog of the TVEM. The model has the same three inputs as the MVM (Figure 1b): the pump speed $N_\mathrm {vad}(t)$, the unstressed volume of the systemic veins $V_\mathrm {0,sv}(t)$, and the heart rate $\mathrm {HR}(t)$. The pulmonary and systemic circulations are implemented as described in Section Pulmonary and Systemic Circulations. The heart consists of the right and left ventricles and four valves as described in the following paragraphs.

Table 1 lists all parameters needed to simulate the TVEM and the MVM. The parameter $f_\mathrm {sys}$ is only used in the MVM and the parameters $\Phi _1$ and $\Phi _2$ are only used in the TVEM. All other parameters are used in both models.

Valve Flows

The flows through the mitral and the tricuspid valves are modelled by algebraic equations (no intertances) and are calculated by

$$\begin{aligned} q(t) = {\left\{ \begin{array}{ll} \frac{p_\mathrm {up}(t) - p_\mathrm {down}(t)}{R} &{} p_\mathrm {up}(t) > p_\mathrm {down}(t) \\ 0 &{} {\rm otherwise}, \end{array}\right. } \end{aligned}$$

where $p_\mathrm {up}(t)$ and $p_\mathrm {down}(t)$ are the pressures upstream and downstream of the valve and R is the valve resistance. The flow through the aortic and pulmonary valve $q_\mathrm {valve}(t)$ is calculated by the differential equation

$$\begin{aligned} {\frac{\mathrm {d}}{\mathrm {d}t}q_\mathrm {valve}(t) = \frac{1}{L_\mathrm {valve}}\cdot \big (p_\mathrm {ventricle}(t)-p_\mathrm {artery}(t) - R_\mathrm {valve}\cdot q_\mathrm {valve}(t)\big ), } \end{aligned}$$

for the aortic valve flow, $p_\mathrm {ventricle}(t)$ and $p_\mathrm {artery}(t)$ are the pressures in the LV and the systemic arteries (aorta), respectively, $L_\mathrm {valve}$ is the inertance, and $R_\mathrm {valve}$ is the resistance of the aortic valve, respectively. Similarly, for the pulmonary valve flow, $p_\mathrm {ventricle}(t)$ and $p_\mathrm {artery}(t)$ are the pressures in the RV and the pulmonary arteries, respectively, $L_\mathrm {valve}$ is the inertance, and $R_\mathrm {valve}$ is the resistance of the pulmonary valve, respectively. The integrator used to solve this differential equation needs to be limited to non-negative values, such that no back flow is possible.

LVAD Flow

The flow through the LVAD $q_\mathrm {vad}(t)$ is calculated by

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}q_\mathrm {vad}(t) = \frac{1}{L_\mathrm {vad}} \cdot \Big (p_\mathrm {lv}(t) - p_\mathrm {sa}(t) + k_\mathrm {vad}\cdot N_\mathrm {vad}^2(t) - R_\mathrm {vad}\cdot q_\mathrm {vad}(t)\Big ), \end{aligned}$$

where $k_\mathrm {vad}$, $R_\mathrm {vad}$, and $L_\mathrm {vad}$ are the gain, the resistance and the inertance of the LVAD, respectively.

Ventricular Volumes

The RV volume is calculated by the differential equation

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}V_\mathrm {rv}(t) = q_\mathrm {tv}(t) - q_\mathrm {pv}(t), \end{aligned}$$

where $q_\mathrm {tv}(t)$ and $q_\mathrm {pv}(t)$ are the tricuspid and the pulmonary valve flows, respectively. The LV volume is calculated by

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}V_\mathrm {lv}(t) = q_\mathrm {mv}(t) - q_\mathrm {av}(t) -q_\mathrm {vad}(t), \end{aligned}$$

where $q_\mathrm {mv}(t)$ is the mitral valve flow.

Ventricular Pressures

The pressures in both ventricles are calculated by

$$\begin{aligned} p_\mathrm {}(t) = E_\mathrm {}(t)\cdot \big (V_\mathrm {}(t) - V_\mathrm {0}(t)\big ), \end{aligned}$$

where $E_\mathrm {}(t)$ is the time-varying elastance, which is calculated by

$$\begin{aligned} E_\mathrm {}(t) = E_\mathrm {min} + \big (E_\mathrm {max}-E_\mathrm {min}\big )\cdot F_{i}(t). \end{aligned}$$

The parameters $E_\mathrm {min}$ and $E_\mathrm {max}$ are the minimum and maximum elastances, respectively and $F_{i}(t)$ is the time-varying interpolation function calculated by

$$F_{i} (t) = \left\{ {\begin{array}{lll} {\frac{1}{2} + \frac{1}{2}\cos \left( {\pi - \frac{{\pi \cdot \varphi (t)}}{{\Phi _{1} }}} \right)} \hfill & {0 \le \varphi \le \Phi _{1} } \hfill & {} \hfill \\ {\frac{1}{2} + \frac{1}{2}\cos \left( {\frac{{\pi \cdot \Phi _{1} }}{{\Phi _{1} - \Phi _{2} }} - \frac{{\pi \cdot \varphi }}{{\Phi _{1} - \Phi _{2} }}} \right)} \hfill & {\Phi _{1} < \varphi (t) \le \Phi _{2} } \hfill & {} \hfill \\ 0 \hfill & {{\text{otherwise}},} \hfill & {} \hfill \\ \end{array} } \right.$$

where $\varphi (t)$ describes the cardiac phase calculated by

$$\begin{aligned} \varphi (t) = {\rm mod} \left( \int _0^t \frac{\mathrm {HR(\tau )}}{60}\ \mathrm {d}\tau ,1 \right) \cdot 2\pi . \end{aligned}$$