1 Introduction

The field of real options theory took off with the seminal book by [12]. This book considers the standard problem of a firm that needs to find the optimal time to undertake a lumpy investment project. The two key assumptions regarding this project are that investment is irreversible and revenues are subject to ongoing uncertainty. The major result is that, given these assumptions, the firm has an incentive to delay its investment in order to wait for more information, and this “value of waiting” goes up if the economic environment becomes more uncertain. Dixit and Pindyck [12] also provide a profound overview of the contributions that appeared up until that time.

From the nineties on, this field has been extended by considering situations where more firms are active in one market. Firms face investment options, where, in case one firm invests, the value of the investment options of other firms is reduced because of the increased competition on this market. Adding competition to the real options framework provides an incentive for the firms to invest quickly in order to preempt investments of other firms, so that they enter the market first and gain (temporary) monopoly profits. On the other hand, it still holds that uncertainty and irreversibility generate a value of waiting effect, so that an interesting trade-off arises. Smets [27] is the first contribution in this area. It considers a framework of a duopoly market where the firms can enlarge an existing profit flow. Grenadier [15] is an early survey of this literature. The survey by [21] focuses on identical firms in a duopoly context. This paper argues that, since firms are identical, it is natural to consider symmetric strategies. This results in obvious coordination problems in situations where it is only optimal for one firm to invest.Huisman et al. [21] show that application of mixed strategies, originally developed by [14] for a deterministic framework, provides a meaningful way to deal with such coordination problems.

The survey by [8] provides an overview of the strategic real options literature where it explicitly considers first- versus second-mover advantage, the role of information, firm heterogeneity, capital increment size, and the number of competing firms. Azevedo and Paxson [4] contain a survey on different game-theoretic aspects of real options models including degree of competition, asymmetries between firms, information structure, cooperation between firms, and market sharing.

The main bulk of the real options literature sees an investment problem as a timing problem. In particular, a firm should find the optimal time to undertake an investment project of given size. However, in most investment problems, it is also important to determine the capacity size a firm will invest in. This is recognized by [18, p.1828] in a review of [12], which argues that “the new view models \(\ldots \) do not offer specific predictions about the level of investment. To go this extra step requires the specification of structural links between the marginal profitability of capital and the desired capital stock.”

The present paper intends to survey the literature that considers investment problems from the view that both timing and size need to be determined. We concentrate on continuous time models where investments have a lumpy structure, thus leaving aside discrete time models (e.g., [13]) and the literature where firms can increase capacity by infinitesimal increments (see, e.g., [1, 2, 16]).

The real options literature that concentrates on investment timing only has a standard result in that uncertainty generates a value of waiting with investment. When also size needs to be determined, the papers reviewed here have a common result that, in a more uncertain economic environment, firms invest later and in a larger capacity size. So, where from the traditional real options literature it could easily be concluded that uncertainty is bad for growth, this is not so clear anymore when also capacity size needs to be determined. This illustrates how important it is to study the capacity issue next to the timing decision.

The paper consists of two parts. Section 2 reviews monopoly models, whereas Sect. 3 includes strategic interactions by focusing on duopolies. Section 2 starts out by presenting the model by [10]. In this model, the firm can invest in a project where price is linearly decreasing in quantity. At the moment the firm invests, it also chooses capacity, and it holds that investment costs are increasing in capacity size. Hereafter, we present [17] that extend [10] by considering different demand functions and determining capacity utilization rates immediately after the investment has taken place. Remarkable is that these utilization rates can be quite low. Apparently, in such cases, firms install capacity mainly to anticipate on future growth and upward demand shocks. Section 2 proceeds by presenting the model by [11]. Here, the performance of the investment project is subject to a learning effect. The size of the capacity positively influences the speed of learning. Therefore, determining optimal capacity size is also an important input in this respect. Section 2 ends by giving an overview of the remaining contributions analyzing one-firm models where both investment timing and investment size need to be determined.

Section 3 starts out by presenting the duopoly model of [20] . The ability to choose capacity enables the first investor to delay investment of the other firm by overinvesting. In this way, overinvestment serves two purposes: not only to reduce capacity of the competitor but also to delay the competitor’s investment. This research introduces strategies such as entry deterrence (second investor invests later) and entry accommodation (firms invest at the same time) to the real options analysis. Next, we present the study by [7]. In models where capacity size and thus quantity can be varied, a crucial model feature is the demand function. Boonman and Hagspiel [7] analyze the implications of different demand functions for strategic firm investment behavior. Where in [20] a new market model is considered, i.e., initially firms are not active yet, [19] extend the Huisman–Kort analysis to an incumbent–entrant framework. Here, initially one firm is an active producer, whereas the other firm is a potential entrant. The final study we extensively present in this section is [23]. This contribution extends [3], where a framework is studied with two known possible entrants and one potential entry by a hidden firm, to allow for capacity choice by the known entrants. Situations are considered where, provided this entry takes place, the hidden firm will enter with either a large or a small capacity. Section 3 is closed by reviewing remaining contributions in this area.

A final Sect. 4 will conclude this survey.

2 Monopoly Models

Dangl [10] is one of the first papers to analyze a model that includes both investment timing as well as size. It considers a framework with one firm that can undertake an investment to enter the market. The price at time t in this market is given by

$$\begin{aligned} P\left( X\left( t\right) , q\left( t\right) \right) =X\left( t\right) -\eta q\left( t\right) , \end{aligned}$$
(1)

where \(q\left( t\right) \) is total market output, \(\eta >0\) is a constant, and \(X\left( t\right) \) is an exogenous shock process. It is assumed that \( X\left( t\right) \) follows a geometric Brownian motion process:

$$\begin{aligned} \mathrm {d}X\left( t\right) =\mu X\left( t\right) \mathrm {d}t+\sigma X\left( t\right) \mathrm {d}\omega \left( t\right) , \end{aligned}$$
(2)

in which \(\mu \) is the drift rate, \(\mathrm {d}\omega \left( t\right) \) is the increment of a Wiener process, and \(\sigma >0\) is a constant. The firm is risk neutral and discounts against rate r. To make sure that the firm will not postpone investment forever, it is assumed that \(r>\mu \). A firm can become active on this market by investing in capacity K,  where the investment costs are equal to \(I\left( K\right) =\delta K^{\gamma },\) with \(\gamma \le 1\). The marginal production costs are equal to \(c^{\prime }\left( K\right) .\) The firm can adjust its output instantaneously between 0 and K. Optimizing the instantaneous profit \(\pi \left( X,K,q\right) =\left( P\left( X,q\right) -c^{\prime }\left( K\right) \right) q\) gives the following optimal output quantity

$$\begin{aligned} q\left( X,K\right) =\left\{ \begin{array}{l@{\quad }l} 0 &{} X<c^{\prime }, \\ \frac{X-c^{\prime }}{2\eta } &{} c^{\prime }\le X<c^{\prime }+2\eta K, \\ K &{} c^{\prime }+2\eta K\le X. \end{array} \right. \end{aligned}$$
(3)

From Eq. (3), it can be derived that there are two boundary values \(X_{1}=c^{\prime }\) and \(X_{2}=c^{\prime }+2\eta K,\) which can be used to define three regions: \(R_{1}=\left[ 0,X_{1}\right) ,R_{2}=\left[ X_{1},X_{2}\right) ,\) and \(R_{3}=\left[ X_{2},\infty \right) .\) The profit under the optimal output is then given by

$$\begin{aligned} \pi \left( X,K,q\left( X,K\right) \right) =\left\{ \begin{array}{l@{\quad }l} 0 &{} X\in R_{1}, \\ \frac{\left( X-c^{\prime }\right) ^{2}}{4\eta } &{} X\in R_{2}, \\ \left( X-c^{\prime }\right) K-\eta K^{2} &{} X\in R_{3}. \end{array} \right. \end{aligned}$$
(4)

The value of the active firm is denoted by \(V\left( X,K\right) \) and is equal to

$$\begin{aligned} V\left( X,K\right) =E\left[ \,\,\, \int \limits _{t=0}^{\infty }\pi \left( X\left( t\right) ,K,q\left( X\left( t\right) ,K\right) \right) \hbox {e}^{-rt}\hbox {d}t\right] . \end{aligned}$$
(5)

Using dynamic programming, [10] shows that

$$\begin{aligned} V\left( X,K\right) \!=\!\left\{ \begin{array}{l@{\quad }l} A_{1,1}\left( K\right) X^{\beta _{1}} &{} X\in R_{1}, \\ A_{2,3}\left( K\right) X^{\beta _{1}}+A_{2,1}\left( K\right) X^{\beta _{2}}+ \frac{1}{4\eta }\left( \frac{X^{2}}{r-2\mu -\sigma ^{2}}-\frac{2c^{\prime }X }{r-\mu }+\frac{\left( c^{\prime }\right) ^{2}}{r}\right) &{} X\in R_{2}, \\ A_{3,2}\left( K\right) X^{\beta _{2}}+\frac{XK}{r-\mu }-\frac{\eta K^{2}+c^{\prime }K}{r} &{} X\in R_{3}. \end{array} \right. \nonumber \\ \end{aligned}$$
(6)

In region \(R_{1}\), the firm is not producing and its value is equal to the option to restart its production when X enters region \(R_{2}\). In region \( R_{2}\), the value of the firm consists of three terms. The first term is the correction for the fact that the output is bounded once X enters region \( R_{3}.\) The term with \(A_{2,1}\left( K\right) \) is the value of the option to suspend production whenever X enters region \(R_{1},\) and the third term is the discounted value of the future profit flow if the firm would not be bounded by a capacity constraint and not be able to suspend production. Finally, in region \(R_{3}\), the value is equal to the value of the option that enables the firm to adjust its production when X enters region \(R_{2}\) and the last two terms reflect the value of a firm that would always produce up to capacity K.

Dangl argues that the value function should be continuous and differentiable at the two boundary values. This leads to four equations that can be solved to derive the four unknowns \((A_{1,1},A_{2,3},A_{2,1},\) and \(A_{3,2})\) from Eq. (6).

At the moment of the investment, the firm can choose its capacity K optimally, so that its value then equals

$$\begin{aligned} \max _{K\ge 0}\left( V\left( X,K\right) -I\left( K\right) \right) . \end{aligned}$$
(7)

The condition for an inner extremum is

$$\begin{aligned} \frac{\partial }{\partial K}\left( V\left( X,K\right) -I\left( K\right) \right) =0. \end{aligned}$$
(8)

In [10], Eq. (8) is solved numerically by using Eq. (6) to derive \(K^{*}\left( X\right) .\) In other words, it gives for each value of X the optimal capacity K that the firm should invest in.

Before investment, the value of the firm is denoted by F. With dynamic programming techniques (see [12]), it is derived that

$$\begin{aligned} F\left( X\right) =C_{1}X^{\beta _{1}}. \end{aligned}$$
(9)

The optimal investment trigger \(X^{*}\) and the constant \(C_{1}\) can be found by solving the value matching and smooth pasting conditions:

$$\begin{aligned} C_{1}\left( X^{*}\right) ^{\beta _{1}}= & {} V\left( X^{*},K^{*}\left( X \right) \right) -I\left( K^{*}\left( X^{*}\right) \right) , \end{aligned}$$
(10)
$$\begin{aligned} \beta _{1}C_{1}\left( X^{*}\right) ^{\beta _{1}-1}= & {} \left. \frac{\partial }{\partial X}\left( V\left( X,K^{*}\left( X\right) \right) -I\left( K^{*}\left( X\right) \right) \right) \right| _{X=X^{*}}. \end{aligned}$$
(11)

Dangl numerically shows the main result of his paper: The optimal installed capacity increases with uncertainty as well as with the investment timing. Thereby, the standard real options result, stating that if uncertainty goes up, the firm delays its investment, is modified to, if uncertainty goes up, a firm will invest later in a larger capacity .

2.1 Value of Flexibility

Hagspiel et al. [17] extend the analysis of [10] by studying a flexible and an inflexible scenario. The flexible firm can costlessly adjust production over time with the capacity level as the upper bound, while the inflexible firm fixes production at capacity level from the moment of investment onwards.

They add holding costs \(c_{h}K\) for holding K units of capacity. Therefore, Eq. (4) becomes

$$\begin{aligned} \pi \left( X,K,q\left( X,K\right) \right) =\left\{ \begin{array}{l@{\quad }l} -c_{h}K &{} X\in R_{1}, \\ \frac{\left( X-c^{\prime }\right) ^{2}}{4\eta }-c_{h}K &{} X\in R_{2}, \\ \left( X-c^{\prime }\right) K-\eta K^{2}-c_{h}K &{} X\in R_{3}. \end{array} \right. \end{aligned}$$
(12)

In the paper, the authors derive explicit expressions for the four constants \( A_{i,j}\left( K\right) \) in Eq. (6). Also, the authors show that it can be the case that a firm does not choose the inner extremum defined in Eq. (8), but a boundary solution. Moreover, [17] state that it can be optimal for the firm to invest in region \(R_{2},\) i.e., the firm invests and starts producing at an output level that is lower than its maximal capacity.

The authors find that the flexible firm invests in a larger capacity than the inflexible firm, where the capacity difference increases with uncertainty. For the flexible firm, the initial capacity utilization rate can be quite low, especially when investment costs are concave and the economic environment is uncertain. When we compare the timing of the investment of the flexible and the inflexible firm, there are two contrary effects. First, the flexible firm has an incentive to invest earlier, because flexibility raises the project value. Second, the flexible firm has an incentive to invest later, as its costs are larger due to the higher capacity level. The latter effect dominates in highly uncertain economic environments.

Studying the effect of increasing capacity holding cost on the optimal investment strategy, the authors find that it is non-monotonic: The optimal capacity size decreases in holding cost for low values of capacity holding cost, while it increases for high ones. The optimal investment threshold, however, is increasing monotonically in capacity holding cost. Defining a firm with low (high) holding cost as a labor-intensive (capital-intensive) firm, it is obtained that the utilization rate in case of capital- intensive industries is high, while it can be significantly low for a labor-intensive firm. The labor-intensive firm invests in higher capacity than the capital-intensive firm but leaves a large amount of this capacity idle at the moment of investment.

The paper studies robustness of their results by also analyzing a scenario where \( \gamma >1\) (convex investment costs). It is found that, when uncertainty goes up, the firm decides to invest significantly later in slightly more capacity in the convex case. This is an expected result since the investment cost the firm is facing for the convex case is significantly higher for larger investments, and therefore, installing a large amount of capacity is more expensive. So, despite the higher investment threshold occurring in the case of more uncertainty, the firm refrains from investing in a very large capacity.

An additional robustness result is that the main result of the comparison between flexible and inflexible firm is confirmed in case of an iso-elastic inverse demand function:

$$\begin{aligned} P\left( t\right) =X\left( t\right) \left( q\left( t\right) \right) ^{-\epsilon }, \end{aligned}$$
(13)

with \(\epsilon \in \left( 0,1\right) \).

2.2 Learning

Della Seta et al. [11] analyze the investment decision of a firm that can invest in a technology involving a learning curve. After investment, the firm may face initial losses, but it learns over time leading to more efficient production, which is exemplified by lower production cost. The firm makes two decisions: It needs to decide upon the moment of investment and upon the scale of its installment. Generally speaking, as a result of capacity choice, two effects come into play in the decision making of the firm: timing and size. Therefore, the firm has two means to reach a certain efficiency level. One option is to invest relatively late and set a large capacity. The main advantage is that the firm learns at a faster pace, but it lowers its current value as a result of discounting. The other option is to invest relatively early leading to an immediate revenue flow. However, investing early means undertaking a small investment, which makes the firm move slowly along the learning curve. The former is called “exploiting the scale option,” and the latter is called “exploiting the timing option.”

A firm is assumed to have an option to undertake an irreversible investment once with lumpy costs. The firm is free to set its capacity K, but it is assumed that the production \(q_{t}\) per unit of time is equal to the maximal amount the capacity allows. As a result, the total cumulative output \(Q_{t}=\int _{0}^{t}q_{s}\ \mathrm {d}s\) equals Kt. The instantaneous cost function c(Q) is defined as

$$\begin{aligned} c(Q)=ce^{-\kappa Q}. \end{aligned}$$
(14)

Here, \(\kappa \ge 0\) reflects the intensity of the learning process, i.e., a larger \(\kappa \) is equivalent to a steeper learning curve. The market price P is equal to Eq. (1). The resulting instantaneous profit flow can be written as \(\pi =(P-c(Q))K\). Investment requires a linear investment cost \(I(K)=\delta K\). Discounting takes place under a fixed rate r.

Della Seta et al. [11] first consider two benchmark models, where either the investment moment or the investment size is fixed. In the first model, the firm has only the option to choose the investment size \(\bar{K}\), but the investment moment is fixed. The second model looks at the opposite case where the firm optimizes the investment moment \(\bar{X}\) under fixed capacity. The paper shows that if the firm can only choose the size, optimal capacity is an increasing function of \(\kappa \). When the scale of investment is fixed, investment is undertaken earlier when the learning curve is steeper, i.e., \(\bar{X}(K)\) is decreasing in \(\kappa \).

The effect of \(\kappa \) is undetermined ex-ante, when firms optimize both timing and scale, for there are two—possibly opposing— effects on the investment moment. Writing out the effect of \(\kappa \) gives

$$\begin{aligned} \frac{\mathrm {d}\bar{X}(\bar{K})}{\mathrm {d}\kappa }=\frac{\partial \bar{X}( \bar{K})}{\partial \kappa }+\frac{\partial \bar{X}(\bar{K})}{\partial \bar{K}} \frac{\partial \bar{K}}{\partial \kappa }. \end{aligned}$$
(15)

The first term is always negative, but the second term is ambiguous. Nevertheless, since the first term is always dominant, investment is accelerated when the learning curve is steeper, i.e., \(\frac{\mathrm {d}\bar{X} (\bar{K})}{\mathrm {d}\kappa }<0\).

When analyzing the effect of \(\kappa \) on the investment size, a few things can be said. First, optimal capacity \(\bar{K}\) is a non-monotonic function of \(\kappa \). There exists a \(\kappa ^{*}\) such that for \(\kappa <\kappa ^{*}\), it is increasing, while for the opposite case \(\kappa >\kappa ^{*}\), the investment scale is a decreasing function of \(\kappa \). Two benchmark cases,

$$\begin{aligned} \bar{K}=\frac{r\delta +c}{(\beta _{1}-2)\eta },&\ \ \ \text { for }\kappa =0, \end{aligned}$$
(16)
$$\begin{aligned} \bar{K}=\frac{r\delta }{(\beta _{1}-2)\eta },&\ \ \ \text { for }\kappa \rightarrow \infty , \end{aligned}$$
(17)

make clear that one can define a \(\widehat{\kappa }>0\) such that the investment size for the case of \(\kappa =\widehat{\kappa }\) is the same as when \(\kappa =0\). Notice that the first benchmark case leads to a flat learning curve. The authors conclude that when \(\kappa <\widehat{\kappa }\), firms set a large capacity when investing in a learning technology, relative to a firm with constant marginal production costs, while delaying investment: They exploit the scale option. The opposite holds for the other case, i.e., for steep learning curves firms invest sooner at a smaller scale: They exploit the timing option. Intuitively, when the learning curve is relatively flat, the firm needs a sufficiently large amount of capacity to reach a desired speed of learning. Additional capacity contains more value relative to the case of a more steep curve. As a result, the gain from additional capacity for flat curves is larger than the loss from delaying investment. However, one supplementary unit of capital when curves are steep leads to relative smaller added value, for the speed is already accelerated by a large value of \(\kappa \). This means that for steep curves, investing earlier at a small amount yields a larger value than waiting to invest at a larger amount.

It is quite likely that investing in a learning curve technology leads to initial losses. An exampleFootnote 1 shows that losses already occur for \(\kappa =0.015\), indicating that negative initial gains are faced, in most cases, for only extremely flat curves show positive initial flows. For relatively small values of \(\kappa \), accumulated losses increase if the learning curve becomes steeper. Contrarily, for relatively large values of \(\kappa \), a steeper curve makes the accumulated losses decrease. In the latter case, the timing option is exploited, so that the firm invests in a relatively small capacity. This brings down the costs, resulting in a smaller loss.

2.3 Others

We give here an overview of contributions based on one-firm models that are used to determine the optimal investment time and the corresponding size of the investment, where, as stated before, we leave out the works that deal with incremental investments. Manne [25] is the first paper to find that the firm invests in a larger capacity level when uncertainty increases. In the same publication year as [5, 10] also have the result that in a more uncertain economic environment, the firm invests later but increases the size of the investment. In their model, the quantity aspect is represented by a capital stock. Investment costs are a linear function of the acquired capital stock, and production is concavely increasing with capital stock. The output price follows a geometric Brownian motion process while being independent of the production quantity. The model also includes a constant marginal production cost, where, analogous to the uncertainty result, an increase in this marginal production cost raises the size of the investment, which will, however, take place at a later point in time.

Bøckman et al. [6] use this method to analyze hydropower projects. The contribution margin, being the difference between the electricity price and the unit production cost, behaves according to a geometric Brownian motion process. Consequently, with its quantity, the hydropower firm does not influence price, which is motivated by stating that the hydropower plants under consideration are small. Bøckman et al. [6] adopts the same exponential relationship between investment cost and capacity as [10]. Parameters are estimated and simulations are carried out to perform case studies regarding three different Norwegian small hydropower projects.

Sarkar [26] introduces the possibility of debt financing to this analysis, where numerical results are generated. In general, [26] also finds that a postponed investment enlarges the size of the investment. There are exceptions however. In particular, it is obtained that when tax rate or bankruptcy costs increase, the firm invests later in a smaller capacity. Also the addition of debt financing makes that the firm invests later in a larger size. The uncertainty effect again means that a more uncertain environment induces a later and larger investment, and, in addition, reduces the leverage ratio. Sarkar [26] imposes that the firm produces up to capacity. As in [10], the investment cost as function of capacity is a power function. As in [5], the firm has no market power, i.e., capacity does not influence price. Instead, the latter follows a geometric Brownian motion process. In addition, the firm also has to decide on the financing mix in the sense that it has to decide how much of the investment is financed by debt. A coupon payment, which is linearly decreasing with the debt level that the firm has to decide on, is subtracted from the instantaneous profit. The profit is taxed where the tax rate is fixed. Besides deciding on the level of debt, and the investment timing and size, the model also allows a bankruptcy decision, where a separation is made between the decision of the shareholders (after bankruptcy declared by them, the firm will be owned by the bondholders, where shareholders have to pay bankruptcy costs with \(\alpha \) being the relevant fraction) and the bondholders. The latter have the opportunity to let the firm go bankrupt after the shareholders have done so. This becomes relevant in case the price keeps on falling after the bankruptcy declaration of the shareholders.

Chronopoulos et al. [9] study the impact of risk aversion in a model where the firm also has the option to suspend operations. Risk aversion is modeled by adopting a concave CRRA utility function. Product price is completely determined by a geometric Brownian motion process, so the firm has no market power. There is a constant operating project cost. Investment costs are a convex and increasing function in size. A major result is that risk aversion reduces capacity size. The consequence is that the firm invests sooner, because it is cheaper due to the smaller investment size. In addition, the common result that increasing uncertainty delays investment and increases investment size is also obtained.

3 Duopoly Models

Huisman and Kort [20] present a complete analysis of a strategic real options model in which both firms have to choose optimal investment timing and capacity. The price is assumed to be equal to

$$\begin{aligned} P\left( X\left( t\right) , q\left( t\right) \right) =X\left( t\right) \left( 1-\eta q\left( t\right) \right) , \end{aligned}$$
(18)

where \(q\left( t\right) \) is total market output, \(\eta >0\) is a constant, and \(X\left( t\right) \) is assumed to follow (2). The firm is risk neutral and discounts against rate r. A firm can become active on this market by investing in capacity K. A unit of capacity costs \(\delta \). This implies that a firm investing in a plant with capacity K incurs investment costs being equal to \(\delta K\). They assume that firms produce up to capacity, i.e., for all t after investment it holds that \(q\left( t\right) =K\).

They first solve the model in case firm 1 has a significant cost advantage: firm 1 (2)’s marginal investment costs equal \(\delta _{1}\,(\delta _{2})\), where \(\delta _{1}<\delta _{2}\). As with most sequential games, they also solve the game backwards. The firm that invests second, which turns out to be firm 2, is called the follower. The investment problem of the follower is comparable to the investment problem of a monopolist, as there is no more strategic interaction because the first firm has already exercised its investment option.

The optimal investment trigger and capacity for the follower are given by

$$\begin{aligned} X_{F}^{*}\left( K_{L}\right)= & {} \frac{\beta _{1}+1}{\beta _{1}-1}\frac{ \delta _{2}\left( r-\mu \right) }{1-\eta K_{L}}, \end{aligned}$$
(19)
$$\begin{aligned} K_{F}^{*}\left( K_{L}\right)= & {} \frac{1-\eta K_{L}}{\left( \beta _{1}+1\right) \eta }. \end{aligned}$$
(20)

Given that \(\beta _{1}\) is decreasing in \(\sigma ,\) from Eqs. (19 ) and (20)  it can be easily derived that when uncertainty goes up, the follower will invest later in a larger capacity. The same equations tell that overinvestment, i.e., increasing \(K_{L},\) by the leader, serves two purposes: The follower will invest later and in a lower capacity level.

The next step is to determine the optimal investment decision of the leader. Essentially, the leader has the choice between two investment strategies: entry deterrence or entry accommodation. Entry deterrence occurs whenever the leader chooses a capacity \(K_{L}\) such that \(X<X_{F}^{*}\left( K_{L}\right) ,\) i.e., when the follower invests later in time than the leader. In this model, deterrence is only temporary as the follower will enter the market eventually when X will become large enough. From Eq. (19)  it follows that a deterrence strategy occurs whenever the leader chooses a capacity level \(K_{L}\) larger than \(\widehat{K}_{L}\left( X\right) \) with

$$\begin{aligned} \widehat{K}_{L}\left( X\right) =\frac{1}{\eta }\left( 1-\frac{\left( \beta _{1}+1\right) \delta _{2}\left( r-\mu \right) }{\left( \beta _{1}-1\right) X}\right) . \end{aligned}$$
(21)

The optimal investment trigger and capacity in case of the entry deterrence strategy are given by

$$\begin{aligned} X_{L}^\mathrm{det}= & {} \frac{\beta _{1}+1}{\beta _{1}-1}\delta _{1}\left( r-\mu \right) , \end{aligned}$$
(22)
$$\begin{aligned} K_{L}^\mathrm{det}\left( X_{L}^\mathrm{det}\right)= & {} \frac{1}{\left( \beta _{1}+1\right) \eta }, \end{aligned}$$
(23)

and for the entry accommodation strategy:

$$\begin{aligned} X_{L}^\mathrm{acc}= & {} \frac{\beta _{1}+1}{\beta _{1}-1}\left( 2\delta _{1}-\delta _{2}\right) \left( r-\mu \right) \!, \end{aligned}$$
(24)
$$\begin{aligned} K_{L}^\mathrm{acc}\left( X_{L}^\mathrm{acc}\right)= & {} \frac{1}{\left( \beta _{1}+1\right) \eta }. \end{aligned}$$
(25)

It turns out that there exists an \(\widehat{X}\) such that the firm with the cost advantage will choose the entry deterrence strategy for X lower than \( \widehat{X}\) and entry accommodation for high values of X.

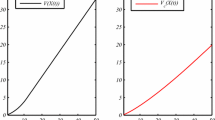
In case there is no or only a small cost difference, the firms will try to preempt each other to become the first investor. In order to analyze these situations, the authors define the value functions for the leader (first investor) \(V_{L}\) and the follower \(V_{F}\) (see Fig. 1). The intersection point \(X_{P}\) defines the moment that the leader will invest and the follower will invest at threshold \(X_{F}^{*}\left( K_{L}^{*}\left( X_{P}\right) \right) ,\) where \(K_{L}^{*}\left( X\right) \) is the optimal investment size for the leader if the geometric Brownian motion process has the level X.

Fig. 1
figure 1

Optimal value functions for the leader \(\left( V_{L}^{*}\right) \) and follower \(\left( V_{F}^{*}\right) \) as function of the X at which the leader invests. Parameter values are \(r=0.1, \mu =0.06, \sigma =0.1, \delta _1 =\delta _2 =0.1\), and \(\eta =0.05\)

Full size image

Huisman and Kort [20] find that the first investor will overinvest not only to tempt the second investor to invest in a smaller capacity but also to let the second investor invest later. In a moderately uncertain environment, the preemption effect dominates, implying that the first investor invests early in a small capacity, so that, in the end, the second investor will be the larger firm. However, in the case with symmetric firms, i.e., \(\delta _1=\delta _2\), the value of waiting effect dominates in highly uncertain economic environments. Then the first investor invests relatively late in a larger capacity level, implying that it will be the larger firm in the market after the second firm has also invested.

3.1 Different Demand Function

Boonman and Hagspiel [7] study the influence of different demand functions as well as different cost structures on the implications of [20]. The authors first consider the combination of linear investment costs and additive demand and compare the results with [20], where multiplicative demand is used. It turns out that in the market with an additive demand structure, the follower always acquires a larger market share, whereas in the market with multiplicative demand, this happens only for sufficiently large uncertainty parameter, \(\sigma ,\) as stated in the previous section. This result arises due to the specific properties of the demand functions. In the market with additive inverse demand, a larger stochastic profitability, X, always implies that the firms are able to choose a larger capacity level. In contrast, in the case of the multiplicative demand function, the firms are bounded in increasing their capacity level even if X is large. Hence, in the latter scenario, the exogenous follower being limited in its capacity choice does not gain a lot by waiting for larger X. This does not hold for the additive demand, as its structure implies that after the market leader has invested, it is optimal for the follower to wait for a larger market size and acquire a larger capacity. Thus, the follower captures the largest market share, while the leader experiences a longer period of monopoly profits. If the roles of the firms are not assigned beforehand, this result becomes even more powerful as the leader is forced to invest earlier and, thus, in a smaller capacity due to the preemption effect. In the endogenous game with multiplicative demand, high uncertainty allows to obtain a similar result, because a more uncertain environment generates a larger value of waiting. Consequently, the leader is induced to undertake investment later and to acquire a larger capacity level.

The next set of results of the paper is associated with the analysis of the firms’ cost structure. The authors assume that, apart from the investment costs proportional to capacity, firms face some certain fixed costs. In particular, the investment costs are now equal to \(\delta _{1}K+\delta _{0}\). This allows to include the iso-elastic demand structure in the analysis.Footnote 2 This demand function is given by (13), and similarly to the additive demand function, it allows the market to grow indefinitely large. In general, an increase in the cost function parameters has two differently directed effects on the capacity choice. On the one hand, an increase in investment costs directly affects the attractiveness of the investment opportunity, i.e., the more expensive it is to enter the market, the smaller capacities will be chosen by the firms. On the other hand, it affects the capacity choice indirectly through investment timing. As a result of larger investment costs, the firms delay their entry decisions, which leads to larger capacity levels at the moment of investment. It has been revealed that if the constant component of investment costs, \(\delta _{0}\), is increased, the indirect effect dominates, causing the firms to invest later and in a larger capacity irrespectively of the demand function choice. However, when the variable component, \(\delta _{1}\), is considered, the implications differ among the demand structures. Under additive demand, the indirect effect of an increase in \(\delta _{1}\) dominates, leading to a delay of the firms’ investment decisions and to a larger capacity installed. However, once the multiplicative or iso-elastic types of the demand function are analyzed the direct effect becomes dominant, causing the capacities to decline with \(\delta _{1}\). This difference comes from the fact that an increase in the stochastic component of the additive demand process has a direct implication for the potential capacity expansion, namely the larger is X, the larger is the potential of an increase in the total market size.

3.2 Incumbent–Entrant

A substantial part of the literature considers investment in new markets. Real-life investment, however, also takes place on existing markets. Despite that there exists a considerable literature stream studying the problem of an incumbent and an entrant within the theory of Industrial Organization, [19] are the first to consider this problem in a dynamic setting with capacity choice. This follow-up on [20] reconsiders the investment decisions of two investors, assuming one of the two firms already being active on the market. Both firms have an option to install (additional) capacity. For the incumbent, this means expansion of its current capacity, and for the entrant, this means market entry.

The setup of the model is similar to [20] assuming the process of X to be sufficiently small, such that neither of the firms prefers to undertake an investment. Essentially, there are three particular investment orders possible. In the first case, the incumbent makes an investment first, followed by the entrant, potentially at some later point in time. In the second case, the order is reversed: The entrant is investment leader, and the incumbent takes the role of the so called follower. Simultaneous investment is the third possible scenario. For both firms, the following pattern is observed. For relatively small values of X, firms prefer not to make an investment first. It would rather prefer the other firm to make an investment so that it can wait for a larger value of X and set a larger capacity. For large X, both firms prefer to become investment leader. As a result, the firms want to preempt each other. It is found that the preemption point of the incumbent is smaller than the preemption point of the entrant. This means that the incumbent makes an investment first, just before the shock process hits the preemption point of the entrant. At that trigger, the incumbent performs a relatively small capacity expansion. The result is that the entrant is temporarily deterred from the market. In this way, the incumbent not only prolongs its monopoly position on the market, but also compensates for the cannibalization effect. This affect arises, since, if either of the firms undertakes an investment, the output price is reduced. This decreases the value of the incumbent’s current production on the market, which is called the cannibalization effect. Hence, by undertaking a small investment first, the incumbent delays the entrant, and at the same time, the cannibalization effect is minimal.

Two additional models give some important insights. In the first model, the same setup is considered, but it is assumed that the investment size is fixed. This results in a reversed investment order. Here, the entrant has a larger incentive to undertake investment first. To explain this, one must realize that the incumbent no longer has the option to undertake a small investment to delay a large investment by the entrant. This implies that there is no way to reduce the cannibalization effect, so that the prime incentive for the incumbent to invest first vanishes.

In the second model, a monopolist is considered that is able to expand its current capacity. This makes it possible to compare the decision making of an incumbent with and without threat of entry by a second firm. It is found that the monopolist waits much longer before it invests, for it faces no threat of entry. As a result, the monopolist sets a larger capacity. This contradicts the main result of the theory of industrial organization that entry deterrence is performed by means of overinvestment; that is, an incumbent would set a larger capacity in the presence of an entrant than that it would without this presence. In other words, entry deterrence is executed through preempting the entrant and not by setting an excessively large capacity.

3.3 Hidden Competition

In [20], it is assumed that market participants have full information about each other. However, in a more realistic setting, firms may not have access to all information about potential entrants. This brings us to [23], where the generalization of the duopoly model in [20] is made in that it is permitted for a hidden third firm to enter the industry. The other two firms that are modeled as explicit players that have no information about the exact investment timing of the hidden firm. As in [3], they only have the knowledge that the hidden firm invests with a probability satisfying a Poisson jump process with mean arrival rate \(\lambda \). The additional assumption made in [23] is that the firms hold a certain belief about the capacity of the hidden player, denoted by \(K_H\). In this setting, the authors analyze the effects of the hidden entrant on the capacity choice and investment timing of the two firms that are well informed about each other, operating in the limited market with only two places available.

The authors first consider the follower’s investment decision in the game with exogenous roles. Given the assumption of the limited market, the value of the follower in the stopping region, i.e., the value obtained after investment, does not change in comparison with [20], as the hidden entrant loses its chance to invest as soon as the second investor enters. However, the value in the continuation region for a given capacity of the leader, i.e., the value of the option to invest, is affected by \(\lambda \) in the following way. If the probability of the immediate hidden entry, \(\lambda \mathrm {d}t\), is large, the follower fears to lose the last available place on the market and, thus, has more incentives to enter this market earlier. In other words, the follower discounts its future payoffs more heavily. Unlike in the follower’s scenario, the exogenous market leader does not lose the option to invest in the case of hidden entry, but when it takes place, it still loses some market share. If the hidden player invests before the explicit follower and acquires capacity level \(K_{H}\), the active leader has to share the market with the hidden player, which in turn affects its value under the deterrence strategy.

When deriving the optimal capacity level of the leader, similarly to [20], the two strategies, accommodation and deterrence, are considered. These strategies are defined in certain regions, namely \( (X_{1}^\mathrm{det},X_{2}^\mathrm{det}]\) and \([X_{1}^\mathrm{acc},\infty )\) respectively. Normally, it holds that \(X_{2}^\mathrm{det}>X_{1}^\mathrm{acc}\), meaning that the optimum for at least one strategy can be reached for \(X>X_{1}^\mathrm{det}\). However, if we assume that the probability and (or) the size of the potential hidden entrant are large enough, this is no longer true. Namely, a large \( \lambda \) and (or) a large \(K_{H}\) change the firms’ strategies in such a way that now \(X_{1}^\mathrm{acc}>X_{2}^\mathrm{det}\). Recall from [20] that there exists a boundary capacity level \(\widehat{K}(X)\), such that the optimal deterrence capacity of the leader satisfies \(K_{L}>\widehat{K}(X)\), while under the accommodation strategy, it holds that \(K_{L}\le \widehat{K}(X)\). Therefore, in the interval \((X_{2}^\mathrm{det},X_{1}^\mathrm{acc})\), the deterrence and accommodation optimums are not available and the market leader chooses the boundary solution, \(\widehat{K}(X)\).

Intuitively, this result can be explained as follows. As mentioned above, when the probability that the hidden firm will occupy the follower’s place on the market and the market is large, the follower becomes more eager to invest. As a result for X in the interval \((X_{2}^\mathrm{det},X_{1}^\mathrm{acc})\), deterring its entry becomes more costly for the leader and it will prefer to enter the market together with the follower. However, in this interval, the market is not big enough to reach maximum profits under the accommodation strategy. Thus, the leader chooses the maximal possible capacity that allows for simultaneous entry, which is \(\widehat{K}(X)\). This strategy leads to the same result in terms of investment timing as the accommodation strategy, i.e., the leader and the follower invest at once, but to a different implication in terms of capacity choice, because the leader invests in a smaller capacity.

The endogenous game is affected by these findings in the following way. Recall that the preemption mechanism induces the first investor to enter the market at the point where the leader and the follower values are equal to each other. In the setting without hidden competition, this point always occurs in the deterrence region, causing sequential investment in the equilibrium. However, once it is allowed for the hidden firm to acquire a relatively large capacity with a sufficiently large probability, the deterrence strategy becomes so expensive that the firms prefer being a follower in the deterrence region. In this case, the preemption point falls into the region where the leader installs the boundary capacity level, \( \widehat{K}(X)\). In this region, the firms invest simultaneously and the difference between the leader and follower payoffs comes from the fact the leader sets its capacity level first. Intuitively, the latter strategy is preferred by the leader facing a large probability of hidden entry as it anticipates that entry deterrence becomes too costly. Moreover, the boundary strategy is more attractive for the firms when the hidden entrant is expected to acquire a large market share: By investing at once, the firms occupy all the available places on the market. Thus, the leader excludes the possibility of both sharing the market with a large hidden player and a decline in price as a result of its entry. Thus, there exists such a combination of the hidden competition parameters that for \(\lambda \ge \lambda _{p}(K_{H})\), a preemptive equilibrium occurs, while for \( \lambda <\lambda _{p}(K_{H})\), a simultaneous equilibrium arises. Furthermore, if the preemption point occurs in the boundary region, the firms enter the market with the same capacity due to the fact that rents at the preemption points are equalized. Hence, when the hidden competition parameters are relatively large, the overinvestment associated with the deterrence strategy does not occur in the equilibrium even when the initial X is low.

Therefore, the main results of this paper are associated with the fact that due to the fear of the hidden entry the follower is more eager to invest and it becomes too costly to deter its entry. Thus, the deterrence strategy can only be implemented for a small market size when the investment is not particularly attractive for the follower. But when the market size is small, also for the leader, it is not profitable to invest. Consequently, the entry accommodation strategy is implemented so that we have a simultaneous equilibrium even in the endogenous game, which is new in the literature.

3.4 Others

Wu [28] studies a setup in which the market is growing until some uncertain point in time and decreases afterward. It turns out that the first investor will choose a smaller capacity than the second investor. In this way, the first investor can make sure that it is better accommodated to the future market decline so that in future, it can end up being a monopolist. The only uncertainty in this model is the switching point of market growth to market decline.

Yang and Zhou [29] consider a duopoly in which one of the firms is an incumbent and the other firm is an entrant. The demand function is linear and of the additive form, where uncertainty is introduced with a geometric Brownian motion process. The investment cost function increases in a non-convex way with capacity size. Production costs consist of a fixed term being linearly increasing with capacity and a variable linear cost term. Production is bounded from above by the capacity level. A crucial assumption is that the incumbent will produce up to capacity after the entrant has invested, but before entry, the incumbent is allowed to produce below capacity level. The paper analyzes the effect of the incumbent’s capacity level on the entry decision, where the incumbent’s decision is given. It is shown that the incumbent can only deter the entry of the entrant temporarily. Eventually, the entrant invests and a duopoly framework results.

Lv et al. [24] consider a duopoly model with an additive linear demand function. The investment costs are linearly increasing with capacity. Additive demand implies that the market can grow indefinitely large. This explains the result that the follower ends up with a larger capacity level than the leader. By waiting for a sufficient amount of time, the market has grown so large that for the follower, it becomes automatically optimal to acquire a large capacity. Greater uncertainty again implies postponed investments and larger investment size of both firms. Lv et al. [24] further obtain that the follower’s capacity grows faster when uncertainty goes up.

Kamoto and Okawa [22] consider a duopoly model with product differentiation in the sense that upon entry, the follower can differentiate its product from the leader’s. Demand is linear and multiplicative, while taking product differentiation into account. Investment costs of both leader and follower are also linear, where the investment costs of the follower go up with the degree of product differentiation. Uncertainty enters via a geometric Brownian motion process. Compared to the endogenous firm roles case, the exogenous leader invests in a larger capacity. Consequently, the follower will differentiate its product more from the leader’s. In the endogenous firm roles case, the follower’s capacity level is larger than the one of the leader.

4 Conclusions

An investment decision involves both choosing the timing as well as the size. So determining timing and size simultaneously adds realism to the theory of real options that mainly considers just timing. The present paper intends to give an overview of the current state of the art in this context. To add even more realism, future contributions could consider issues like giving a firm multiple investment options, exit options, technological progress, innovation, product heterogeneity, environmental policy, entry of additional firms, asymmetric information scenarios, macroeconomic effects resulting in changes in demand over time, and government policies based on welfare analysis. As usual, researchers will face the trade-off between analyzing simple models that allow for full analytical solutions and designing more complex models that could only be solved using numerical methods.