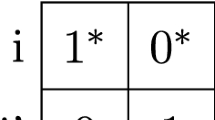
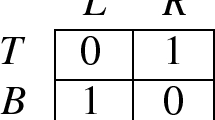
Abstract
We give an example of a zero-sum stochastic game with four states, compact action sets for each player, and continuous payoff and transition functions, such that the discounted value does not converge as the discount factor tends to 0, and the value of the n-stage game does not converge as n goes to infinity.
Similar content being viewed by others
Notes
In which the future has weight 1−λ; we warn the reader that in the literature the opposite convention δ=1−λ is often used.
For a compact metric space K, Δ(K) denotes the set of Borel probabilities on K, endowed with the weak-⋆ topology.
Interestingly, this game was, at the time, a potential example of a finite game with no uniform value. In their example, the payoff does depend on the chosen actions but this is irrelevant as it won’t change the asymptotics of the optimal play.
Their example is the particular case of \(p^{*}_{+}=p^{*}_{-}=1\).
For reasons that will become clear later (division by 1−λ), it is better not to take I=[0,1] but a smaller interval.
We denote C 1(A,B) the set of continuously differentiable functions from A to B.
The function \(\frac{\sin{\ln x}}{16}\) used previously would not work here since its derivative is not a o(1/x).
In particular, any function λ α for α∈]0,1[ satisfies this condition.
References
Aumann RJ, Maschler M, with the collaboration Stearns RE (1995) Repeated games with incomplete information. MIT Press, Cambridge
Bather J (1973) Optimal decision procedures for finite Markov chains. Part I: Examples. Adv Appl Probab 5:328–339
Bather J (1973) Optimal decision procedures for finite Markov chains. Part II: Communicating systems. Adv Appl Probab 5:521–540
Bather J (1973) Optimal decision procedures for finite Markov chains. Part III: General convex systems. Adv Appl Probab 5:541–553
Bewley T, Kohlberg E (1976) The asymptotic theory of stochastic games. Math Oper Res 1:197–208
Bewley T, Kohlberg E (1976) The asymptotic solution of a recursion equation occurring in stochastic games. Math Oper Res 1:321–336
Bewley T, Kohlberg E (1978) On stochastic games with stationary optimal strategies. Math Oper Res 3:104–125
Bolte J, Gaubert S, Vigeral G (2012) Definable zero-sum stochastic games. Preprint
Cardaliaguet P, Laraki R, Sorin S (2012) A continuous time approach for the asymptotic value in two-person zero-sum repeated games. SIAM J Control Optim 50:1573–1596
Dynkin E, Yushkevich A (1979) Controlled Markov processes. Controlled Markov processes. Springer, Berlin
Everett H (1957) Recursive games. In: Kuhn HW, Tucker AW (eds) Contributions to the theory of games, III. Annals of mathematical studies, vol 39. Princeton University Press, Princeton, pp 47–78
Kohlberg E (1974) Repeated games with absorbing states. Ann Stat 2:724–738
Kohlberg E, Neyman A (1981) Asymptotic behavior of nonexpansive mappings in normed linear spaces. Isr J Math 38:269–275
Maitra A, Parthasarathy T (1970) On stochastic games. J Optim Theory Appl 5:289–300
Mertens J-F, Zamir S (1971) The value of two player zero sum repeated games with lack of information on both sides. Int J Game Theory 1:39–64
Mertens J-F, Neyman A, Rosenberg D (2009) Absorbing games with compact action spaces. Math Oper Res 34:257–262
von Neumann J (1928) Zur Theorie der Gesellschaftsspiele. Math Ann 100:295–320
Neyman A (2003) Stochastic games and nonexpansive maps. In: Neyman A, Sorin S (eds) Stochastic games and applications. Kluwer Academic, Dordrecht
Oliu-Barton M (2012) The asymptotic value in finite stochastic games. Preprint
Renault J (2006) The value of Markov chain games with lack of information on one side. Math Oper Res 31:490–512
Renault J (2011) Uniform value in dynamic programming. J Eur Math Soc 13:309–330
Renault J (2012) The value of repeated games with an informed controller. Math Oper Res 37:309–330
Rosenberg D (2000) Zero-sum absorbing games with incomplete information on one side: asymptotic analysis. SIAM J Control Optim 39:208–225
Rosenberg D, Sorin S (2001) An operator approach to zero-sum repeated games. Isr J Math 121:221–246
Rosenberg D, Vieille N (2000) The maxmin of recursive games with lack of information on one side. Math Oper Res 25:23–35
Shapley LS (1953) Stochastic games. Proc Natl Acad Sci USA 39:1095–1100
Sion M (1958) On general minimax theorems. Pac J Math 8:171–176
Sorin S (2002) A first course on zero-sum repeated games. Springer, Berlin
Sorin S (2003) The operator approach to zero-sum stochastic games. In: Neyman A, Sorin S (eds) Stochastic games and applications. Kluwer Academic, Dordrecht
Sorin S (2004) Asymptotic properties of monotonic nonexpansive mappings. Discrete Event Dyn Syst 14:109–122
Sorin S, Vigeral G (2013) Existence of the limit value of two person zero-sum discounted repeated games via comparison theorems. J Optim Theory Appl. doi:10.1007/s10957-012-0193-4
Acknowledgements
This research was supported by grant ANR-10-BLAN 0112 (France).
This paper owes a lot to Sylvain Sorin. I pleasantly remember countless discussions about compact games and why they should have an asymptotic value or not, as well as devising with him a number of “almost proofs” of convergence. This was decisive to understand the right direction to go to stumble upon this counterexample.
I also would like to thank Jérome Bolte for being the first to warn me about non-semialgebraic functions, Jérôme Renault for raising several interesting questions while I was writing this paper, as well as Andrzej S. Nowak for useful references.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vigeral, G. A Zero-Sum Stochastic Game with Compact Action Sets and no Asymptotic Value. Dyn Games Appl 3, 172–186 (2013). https://doi.org/10.1007/s13235-013-0073-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-013-0073-z