Introduction

Nanotechnology is an industrial revolution and one of the hottest fields of research. In the last few years, carbon nanotubes (CNTs) have attracted extensive research activities due to their exceptional mechanical, physical, chemical and thermal properties. CNTs were first discovered by Iijima (1991).

Carbon nanotubes (CNTs) are unique nanostructured materials that comprise a basic element of nanotechnology. Given their extraordinary mechanical and physical properties, together with their large aspect ratio and low density, CNTs are ideal components of nanodevices. Carbon nanotube research is one of the most promising domains in the fields of mechanics, physics, chemistry, and materials science. A wide range of applications of CNTs have been reported in the literature, including applications in nanoelectronics, nanodevices, and nanocomposites (Iijima 1991; Hai-Yang and Xin-Wei 2010; Lai et al. 2008; Deretzis and La Magna 2008; Chowdhury et al. 2009; Mehdipour et al. 2011; Hornbostel et al. 2008; Hwang et al. 2010).

It is important to have accurate theoretical models for the vibrational behavior of CNTs. The natural frequencies of CNTs play an important role in nanomechanical resonators.

Since the vibrations of CNTs are of considerable importance in a number of nanomechanical devices such as oscillators, charge detectors, field emission devices and sensors, many researches have been so far devoted to the problem of the vibrations of CNTs (Ru 2002; Yoon and Ru 2002; Zhang et al. 2005; Yoon et al. 2003). A good review on the vibration of CNTs is given by Gibson et al. (2007) including a concise review of as many of the relevant publications as possible. Based on the theory of thermal elasticity mechanics, Wang et al. (2008) studied the vibration and instability analysis of fluid-conveying single-walled carbon nanotubes (SWNTs) considering the thermal effect.

However, most of the investigations conducted on the vibration of CNTs have been restricted to the linear regime and fewer works were done on the non-linear vibration of these materials. Recently, Fu et al. (2006) studied the non-linear vibrations of embedded nanotubes using the incremental harmonic balanced method (IHBM). In that work, single-walled nanotubes (SWNTs) and double-walled nanotubes (DWNTs) were considered for the study. In recent years, many phenomena in engineering, physics, biology, fluid mechanics and other sciences can be described very successfully using mathematical modeling.

Most differential equations of engineering problems do not have exact analytic solutions so approximation and numerical methods must be used. A great deal of effort has been expended in attempting to find robust and stable numerical and analytical methods for solving differential equations of physical interest.

These numeical methods include the finite difference method (Ghasemi and Mehdizadeh Ahangar 2014), finite element method (Imani et al. 2014) and finite volume method (Ghasemi et al. 2013a, b). Also the analytical methods include the homotopy perturbation method (HPM) (Ghasemi et al. 2013c; Mohammadian et al. 2015), adomian decomposition method (ADM) (Ghasemi et al. 2012), variational iteration method (VIM) (Ghasemi et al. 2012), modified homotopy perturbation method (MHPM) (Ghasemi et al. 2014a), least square method (LSM) (Ghasemi et al. 2014b), optimal homotopy asymptotic method (OHAM) (Ghasemi et al. 2013c; Vatani et al. 2014), differential transformation method (DTM) (Ghasemi et al. 2014c, d), and reconstruction of variational iteration method (RVIM) (Nikaeen et al. 2013).

The Variational iteration method (VIM) is a new approach for finding the approximate solution of linear and non-linear problems using a general Lagrange’s multiplier, which can be determined optimally by variational theory. This method was first proposed by He (Finlayson 1972; He 1997, 1998a, b, c). It has been used to solve effectively, easily and accurately a large class of non-linear problems with approximations. These approximations converge rapidly to accurate solutions.

Ghasemi et al. (2012) investigated the motion of a spherical solid particle in a plane couette fluid flow by variational iteration method. They applied the VIM to solve the couple of equations of a spherical particle motion in a plane Couette fluid flow and their results showed that variational iteration method give approximations of a high degree of accuracy and least computational effort for studying particle motion in Couette fluid flow.

In this paper, an analytical approach based on He’s variational iteration method is suggested to obtain the non-linear vibration of single-walled carbon nanotubes (SWCNTs). Also, the frequency and deflection for vibrations of single-walled carbon nanotubes are investigated in this work.

Mathematical modeling of single-walled carbon nanotube

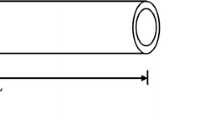
Figure 1 shows a single-walled carbon nanotube (SWCNT) modeled as a Timoshenko nanobeam with length L, radius r, and effective tube thickness h.

Fig. 1
figure 1

A single wall carbon nanotube (SWCNT) modeled as a nonlocal Timoshenko nanobeam

Full size image

It is assumed that the SWCNTs vibrate only in the x–z plane. Based on Timoshenko beam theory, the displacements of an arbitrary point in the beam along the x- and z-axes, denoted by \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{U} \left( {x,z,t} \right) \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{W} \left( {x,z,t} \right) \), respectively, are \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{U} \left( {x,z,t} \right)\, = \,U\left( {x,t} \right)\, + \,z\varphi (x,t) \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{W} \left( {x,z,t} \right)\, = \,W(x,t) \) where U (x, t) and W (x, t) are the displacement components in the midplane, ϕ is rotation of beam cross-section and t is time. The non-linear equations of motion for the nonlocal SWCNTs modeled as a Timoshenko nanobeam is given by:

$$ EA\left( {\frac{{\partial^{2} U}}{{\partial x^{2} }}\, + \,\left( {\frac{\partial W}{\partial x}} \right)\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)} \right)\, = \,\rho A\frac{{\partial^{2} }}{{\partial t^{2} }}\left(U\, - \,\left( {e_{0} a} \right)^{2} \left( {\frac{{\partial^{2} U}}{{\partial x^{2} }}} \right)\right) $$
(1)
$$ \begin{gathered} K_{s} GA\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }} + \frac{\partial \varphi }{\partial x}} \right)\, + \,\varSigma_{1} - \left( {e_{0} a} \right)^{2} \varSigma_{2} \, = \,\rho A\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {W\, - \,\left( {e_{0} a} \right)^{2} \left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)} \right) - \hfill \\ \rho A\left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}\left(\frac{{\partial^{2} U}}{{\partial x^{2} }} - \left( {e_{0} a} \right)^{2} \left( {\frac{{\partial^{4} U}}{{\partial x^{4} }}} \right)\right) \hfill \\ \end{gathered} $$
(2)
$$ EI\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} - K_{s} GA\left( {\frac{\partial W}{\partial x} + \varphi } \right) = \rho I\frac{{\partial^{2} }}{{\partial t^{2} }}(\varphi - \left( {e_{0} a} \right)^{2} \left( {\frac{{\partial^{2} \varphi }}{{\partial x^{2} }}} \right) $$
(3)

where

$$ \varSigma_{1} \, = \,EA(\left( {\frac{{\partial^{2} U}}{{\partial x^{2} }}} \right)\left( {\frac{\partial W}{\partial x}} \right) + \frac{3}{2}\left( {\frac{\partial W}{\partial x}} \right)^{2} \left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) + \left( {\frac{\partial U}{\partial x}} \right)\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)) $$
$$ \begin{gathered} \varSigma_{2} = EA\left( {\left( {\frac{{\partial^{4} U}}{{\partial x^{4} }}} \right)\left( {\frac{\partial W}{\partial x}} \right) + 3\left( {\frac{{\partial^{3} U}}{{\partial x^{3} }}} \right)\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) + 3\left( {\frac{{\partial^{2} U}}{{\partial x^{2} }}} \right)\left( {\frac{{\partial^{3} W}}{{\partial x^{3} }}} \right) + \left( {\frac{\partial U}{\partial x}} \right)\left( {\frac{{\partial^{4} W}}{{\partial x^{4} }}} \right)} \right) + EA(3\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)^{3} + \hfill \\ 9\left( {\frac{\partial W}{\partial x}} \right)\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)\left( {\frac{{\partial^{3} W}}{{\partial x^{3} }}} \right) + \frac{3}{2}(\frac{\partial W}{\partial x})^{2} \left( {\frac{{\partial^{4} W}}{{\partial x^{4} }}} \right)) \hfill \\ \end{gathered} $$

where A is the cross-sectional area of the beam, I is the second moment of area and ρ is the mass density of beam material, E and G are Young’s modulus and shear modulus, respectively. The constitutive relations in classical elasticity theories can be recovered by setting the nonlocal parameter e 0 a = 0 and K s is the shear correction factor depending on the shape of the cross-section of the beam. Introducing the following dimensionless quantities:

$$ \begin{gathered} \zeta \, = \,\frac{x}{L},\,\left( {u,w} \right)\, = \,\frac{(U,W)}{r},\,\varphi \, = \, \psi ,\,\left( {I_{1} ,I_{3} } \right)\, = \,(\frac{\rho A}{\rho A} ,\frac{\rho I}{{\rho Ar^{2} }}),\,\eta = \frac{L}{r}, \hfill \\ \mu \, = \,\frac{{e_{0} a}}{L},\,\left( {a_{11} ,a_{55 } , d_{11} } \right)\, = \,\left(\frac{EA}{EA} ,\,\frac{{K_{s} GA}}{EA} ,\,\frac{EI}{{EAr^{2} }}\right),\,\tau \, = \,\frac{t}{L}\sqrt {\frac{E}{\rho }} \hfill \\ \end{gathered} $$
(4)

Equations (1), (2), (3) can be expressed in dimensionless form as:

$$ a_{11} \left( {\frac{{\partial^{2} u}}{{\partial \zeta^{2} }}\, + \,\frac{1}{\eta }\left( {\frac{\partial w}{\partial \zeta }} \right)\left( {\frac{{\partial^{2} w}}{{\partial \zeta^{2} }}} \right)} \right)\, = \,I_{1} \frac{{\partial^{2} }}{{\partial \tau^{2} }}(u\, - \,\mu^{2} \left( {\frac{{\partial^{2} u}}{{\partial \zeta^{2} }}} \right)) $$
(5)
$$ a_{55} \left( {\frac{{\partial^{2} w}}{{\partial \zeta^{2} }} + \eta \frac{\partial \psi }{\partial \zeta }} \right) + \bar{\varSigma }_{1} \, - \,\mu^{2} \bar{\varSigma }_{2} = I_{1} \frac{{\partial^{2} }}{{\partial \tau^{2} }}\left( {w - \mu^{2} \left( {\frac{{\partial^{2} w}}{{\partial \zeta^{2} }}} \right)} \right) - \frac{{\partial^{2} u}}{{\partial \zeta^{2} }} - \mu^{4} \left( {\frac{{\partial^{4} u}}{{\partial x^{4} }}} \right)) $$
(6)
$$ d_{11} \frac{{\partial^{2} \psi }}{{\partial \zeta^{2} }} - a_{55} \eta \left( {\frac{\partial w}{\partial \zeta } + \eta \psi } \right) = I_{3} \frac{{\partial^{2} }}{{\partial \tau^{2} }}(\psi - \mu^{2} \left( {\frac{{\partial^{2} \psi }}{{\partial \zeta^{2} }}} \right) $$
(7)

where

$$ \bar{\varSigma }_{1} = \frac{{a_{11} }}{\eta }(\left( {\frac{{\partial^{2} u}}{{\partial \zeta^{2} }}} \right)\left( {\frac{\partial w}{\partial \zeta }} \right) + \frac{3}{2\eta }\left( {\frac{\partial w}{\partial \zeta }} \right)^{2} \left( {\frac{{\partial^{2} w}}{{\partial \zeta^{2} }}} \right) + \left( {\frac{\partial u}{\partial \zeta }} \right)\left( {\frac{{\partial^{2} w}}{{\partial \zeta^{2} }}} \right)) $$
$$ \begin{gathered} \bar{\Sigma }_{2} \, = \,\frac{{a_{{11}} }}{\eta }\left( {\left( {\frac{{\partial ^{4} u}}{{\partial \zeta ^{4} }}} \right)\left( {\frac{{\partial w}}{{\partial \zeta }}} \right) + 3\left( {\frac{{\partial ^{3} u}}{{\partial \zeta ^{3} }}} \right)\left( {\frac{{\partial ^{2} w}}{{\partial \zeta ^{2} }}} \right)} \right. \hfill \\ \qquad\left. { + 3\left( {\frac{{\partial ^{2} u}}{{\partial \zeta ^{2} }}} \right)\left( {\frac{{\partial ^{3} w}}{{\partial \zeta ^{3} }}} \right) + \left( {\frac{{\partial u}}{{\partial \zeta }}} \right)\left( {\frac{{\partial ^{4} w}}{{\partial \zeta }}} \right)} \right) \hfill \\ \qquad + \frac{{a_{{11}} }}{{\eta ^{2} }}\left( {3\left( {\frac{{\partial ^{2} w}}{{\partial \zeta ^{2} }}} \right)^{3} + 9\left( {\frac{{\partial w}}{{\partial \zeta }}} \right)\left( {\frac{{\partial ^{2} w}}{{\partial \zeta ^{2} }}} \right)\left( {\frac{{\partial ^{3} w}}{{\partial \zeta ^{3} }}} \right)} \right. \hfill \\ \left. \qquad{ + \frac{3}{2}(\frac{{\partial w}}{{\partial \zeta }})^{2} \left( {\frac{{\partial ^{4} w}}{{\partial \zeta ^{4} }}} \right)} \right) \hfill \\ \end{gathered} $$

Assuming \( \psi \left( {\zeta ,\tau } \right) = u\left( \zeta \right)v(\tau ) \), and \( w\left( {\zeta ,\tau } \right) = f\left( \zeta \right)g(\tau ) \) with ignoring U, where u(ζ), \( f\left( \zeta \right) \) is the first eigenmode of the beam (Tse et al. 1978) and applying the Galerkin method, the equation of motion is obtained as follows:

$$ \textit{\"{g}}\left( \tau \right) + \alpha_{1} g\left( \tau \right) + \alpha_{2} v\left( \tau \right) + \alpha_{3} g^{3} (\tau ) = 0 $$
(8)
$$ \textit{\"{v}}\left( \tau \right) + \beta_{1} v\left( \tau \right) + \beta_{2} g\left( \tau \right) = 0 $$
(9)

where α 1,\( \alpha_{2} \), α 3,\( \beta_{1} \) and β 2 are as follows: \( \alpha_{1} = - a_{55} \frac{{\mathop \smallint \nolimits_{0}^{1} f\left( \zeta \right)f^{\prime \prime } \left( \zeta \right)d\zeta }}{{\mathop \smallint \nolimits_{0}^{1} f^{2} \left( \zeta \right)d\zeta }} \), \( \alpha_{2} = - a_{55} \eta \frac{{\mathop \smallint \nolimits_{0}^{1} u^{\prime } (\zeta )f\left( \zeta \right)d\zeta }}{{\mathop \smallint \nolimits_{0}^{1} f^{2} \left( \zeta \right)d\zeta }} \), \( \alpha_{3} = - \frac{{3a_{11} }}{{2\eta^{2} }}\frac{{\mathop \smallint \nolimits_{0}^{1} f\left( \zeta \right)f^{\prime 2} (\zeta )f^{\prime \prime } \left( \zeta \right)d\zeta }}{{\mathop \smallint \nolimits_{0}^{1} f^{2} \left( \zeta \right)d\zeta }} \),

$$ \begin{gathered} \beta_{1} \, = \, - \frac{{d_{11} }}{{I_{3} }}\frac{{\mathop \smallint \nolimits_{0}^{1} u\left( \zeta \right)u^{\prime \prime } \left( \zeta \right)d\zeta }}{{\mathop \smallint \nolimits_{0}^{1} u^{2} \left( \zeta \right)d\zeta }}\, + \,\frac{{a_{55} \eta^{2} }}{{I_{3} }}, \hfill \\ \beta_{2} \, = \,\frac{{a_{55} \eta }}{{I_{3} }}\frac{{\mathop \smallint \nolimits_{0}^{1} f^{\prime } (\zeta )u\left( \zeta \right)d\zeta }}{{\mathop \smallint \nolimits_{0}^{1} u^{2} \left( \zeta \right)d\zeta }} \hfill \\ \end{gathered} $$
(10)

The Eqs. (8) and (9) are the governing non-linear vibration of Timoshenko beams.

The center of the beam subjected to the following initial conditions:

$$ g\left( 0 \right) = A,\,\dot{g}\left( 0 \right) = 0,\,v\left( 0 \right) = B,\,\dot{v}\left( 0 \right) = 0 $$
(11)

where A, B denotes the non-dimensional maximum amplitude of oscillation.

Fundamentals of variational iteration method

To illustrate the basic concepts of the variational iteration method (VIM), we consider the following differential equation:

$$ Lu + Nu = g(t) $$
(12)

where L is a linear operator, N a non-linear operator and g(t) an inhomogeneous term. According to VIM, we can write down a correction functional as follows:

$$ u_{n + 1} \left( t \right) = u_{n} \left( t \right) + \mathop \smallint \limits_{0}^{t} \lambda \left( {Lu_{n} \left( \eta \right) + N\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u}_{n} \left( \eta \right) - g\left( \eta \right)} \right)d\eta $$
(13)

where λ is a general Lagrange multiplier which can be identified optimally via the variational theory (He 1998a). The subscript n indicates the nth approximation and \( \tilde{u}_{n} \) is considered as a restricted variation \( \delta \tilde{u}_{n} = 0 \).

Results and discussions

To solve Eqs. (8) and (9) by means of VIM, we start with an arbitrary initial approximation:

$$ g_{0} \left( \tau \right) = A\cos \left( {\omega \tau } \right),v_{0} \left( \tau \right) = B\cos \left( {\omega \tau } \right) $$
(14)

From Eq. (8), we have:

$$ \begin{gathered} \textit{\"{g}}\left( \tau \right) = - \alpha_{1} g\left( \tau \right) - \alpha_{2} v\left( \tau \right) - \alpha_{3} g^{3} \left( \tau \right) \Rightarrow \hfill \\ \textit{\"{g}}\left( \tau \right) = - \alpha_{1} A\cos (\omega \tau ) - \alpha_{2} B\cos (\omega \tau ) - \alpha_{3} A^{3} \cos^{3} (\omega \tau ) \hfill \\ \end{gathered} $$
(15)

Integrating twice yields:

$$ g_{1} \left( \tau \right)\, = \,\frac{{\alpha_{1} A\cos (\omega \tau )}}{{\omega^{2} }}\, + \,\frac{{\alpha_{2} B\cos (\omega \tau )}}{{\omega^{2} }}\, + \,\frac{{\alpha_{3} A^{3} }}{4}\left (\frac{\cos (3\omega \tau )}{{9\omega^{2} }}\, + \,\frac{3\cos (\omega \tau )}{{\omega^{2} }}\right) $$
(16)

Equating the coefficients of cos(ωτ) in g 0 and g 1, we have:

$$ \omega_{\text{VIM}} = \sqrt {\alpha_{1} + \frac{{\alpha_{2} B}}{A} + 0.75\alpha_{3} A^{2} } $$
(17)

And therefore,

$$ g_{0} \left( \tau \right) = A\cos \left(\sqrt {\alpha_{1} + \frac{{\alpha_{2} B}}{A} + 0.75\alpha_{3} A^{2 } } \tau \right) $$
(18)

Where \( \delta \tilde{u}_{n} = 0 \) is considered as restricted variation.

$$ g_{n + 1} \left( \tau \right) = g_{n} \left( \tau \right) + \mathop \smallint \limits_{0}^{\tau } \lambda \left( {\frac{{d^{2} g_{n} }}{{d\eta^{2} }} + \alpha_{1} g_{n} + \alpha_{2} v_{n} + \alpha_{3} g_{n}^{3} } \right)d\eta $$
(19)
$$ v_{n + 1} \left( \tau \right) = v_{n} \left( \tau \right) + \mathop \smallint \limits_{0}^{\tau } \lambda \left( {\frac{{d^{2} v_{n} }}{{d\eta^{2} }} + \beta_{1} v_{n} + \beta_{2} g_{n} } \right)d\eta $$
(20)

Its stationary conditions can be obtained as follows:

$$ 1 - \lambda^{\prime } |_{\eta = t} = 0 $$
(21)
$$ \lambda |_{\eta = t} = 0 $$
(22)
$$ \lambda^{\prime \prime } + \omega^{2} \lambda = 0 $$
(23)

Therefore, the multiplier, can be identified as

$$ \lambda = \frac{1}{\omega }\sin \omega (\eta - \tau ) $$
(24)

As a result, we obtain the following iteration formula:

$$ g_{n + 1} \left( \tau \right) = g_{n} \left( \tau \right) + \mathop \int \limits_{0}^{\tau }\left (\frac{1}{\omega }\sin \omega (\eta - \tau )\right)\left( {\frac{{d^{2} g_{n} }}{{d\eta^{2} }} + \alpha_{1} g_{n} + \alpha_{2} v_{n} + \alpha_{3} g_{n}^{3} } \right)d\eta $$
(25)
$$ v_{n + 1} \left( \tau \right) = v_{n} \left( \tau \right) + \mathop \smallint \limits_{0}^{\tau } (\frac{1}{\omega }\sin \omega (\eta - \tau ))\left( {\frac{{d^{2} v_{n} }}{{d\eta^{2} }} + \beta_{1} v_{n} + \beta_{2} g_{n} } \right)d\eta $$
(26)

By the iteration formula (25) and (26), we can directly obtain other components as:

$$ \begin{gathered} g_{1} \left( \tau \right) = A\cos \left( {\omega \tau } \right) + \frac{1}{{32\omega^{2} }}( - \alpha_{3} A^{3} \cos \left( {\omega \tau } \right) + 16\omega^{3} A\tau \sin \left( {\omega \tau } \right) - \hfill \\ 16\omega \alpha_{1} A\tau \sin \left( {\omega \tau } \right) - 16\omega \alpha_{2} B\tau \sin \left( {\omega \tau } \right) - 12\omega \alpha_{3} A^{3} \tau \sin \left( {\omega \tau } \right) + \alpha_{3} A^{3} \cos \left( {3\omega \tau } \right) \hfill \\ \end{gathered} $$
(27)

where ω is evaluated from Eq. (17). In the same manner, the rest of the components of the iteration formula can be obtained.

The frequency of single wall carbon nanotube versus amplitude is plotted in Fig. 2.

Fig. 2
figure 2

Frequency of single walled carbon nanotube versus amplitude

Full size image

Figure 3 shows the effect of amplitude of vibration on frequency of single wall carbon nanotube for different values of B.

Fig. 3
figure 3

Frequency of single walled carbon nanotube versus amplitude for different values of B

Full size image

Figure 4 depicts the deflection of single wall carbon nanotube versus time and amplitude at α 1 = 2.910191164, α 2 = 9.828472866, and α 3 = 0.4357628396 for B = 0.005.

Fig. 4
figure 4

Deflection of single walled carbon nanotube versus time and amplitude at \( \varvec{\alpha}_{1} = 2.910191164 \), \( \varvec{\alpha}_{2} = 9.828472866 \), and \( \varvec{\alpha}_{3} = 0.4357628396 \) for B = 0.005

Full size image

The solutions are also compared for t = 0.5 in Table 1. It can be observed that there is an excellent agreement between the results obtained from VIM with those of fourth-order Runge–Kutta numerical method.

Table 1 Comparison between VIM soloutions with numerical results for g(τ) when t = 0.5 and α 1 = α 2 = α 3 = 1
Full size table

Conclusion

In this work, the non-linear vibrations of single-walled carbon nanotubes (SWCNTs) has been studied using novel computational technique. The Variational iteration method (VIM) is proved to be very convenient and powerful mathematical tool to solving non-linear oscillators and the solutions obtained are in good agreement with numerical values. The proposed method does not require small parameter in the equation which is difficult to be found for non-linear problems. The results show that magnitude of the amplitude for vibration has strong effect on the frequency and deflection of single-walled carbon nanotubes.