Boundary layer flow and heat transfer of viscoelastic nanofluids past a stretching sheet with partial slip conditions

Abstract

The aim of the paper is to analyze the effect of velocity slip boundary condition on the flow and heat transfer of non-Newtonian nanofluid over a stretching sheet. The Brownian motion and thermophoresis effects are also considered. The boundary layer equations governed by the partial differential equations are transformed into a set of ordinary differential equations with the help of group theory transformations. The obtained ordinary differential equations are solved by variational finite element method (FEM). The effects of different controlling parameters, namely, the Brownian motion parameter, the thermophoresis parameter, viscoelastic parameter, Prandtl number, Lewis number and the slip parameter on the flow field and heat transfer characteristics are examined. The numerical results for the dimensionless velocity, temperature and nanoparticle volume fraction as well as the reduced Nusselt and Sherwood number have been presented graphically. The present study is of great interest in the fields of coatings and suspensions, cooling of metallic plates, oils and grease, paper production, coal water or coal–oil slurries, heat exchangers’ technology, and materials’ processing and exploiting.

Introduction

Due to enormous industrial, transportation, electronics, biomedical applications, such as in advanced nuclear systems, cylindrical heat pipes, automobiles, fuel cells, drug delivery, biological sensors, and hybrid-powered engines, the convective heat transfer in nanofluids has become a topic of great interest. Nanofluids are engineered by suspending nanoparticles with average sizes 1–100 nm. (Choi et al. 2001), (Masuda et al. 1993) have shown that a very small amount of nanoparticles (usually <5 %), when dispersed uniformly and suspended stably in base fluids, can provide dramatic improvements in the thermal conductivity and in the heat transfer coefficient of the base fluid. The term ‘nanofluids’ (nanoparticle fluid suspensions) was coined by Choi (1995), to describe this new class of nanotechnology-based heat transfer fluids that exhibit thermal properties superior to those of their base fluids or conventional particle fluid suspensions. The nanoparticles are typically made of oxides such as alumina, silica, titania and copper oxide, carbides, and metals such as copper and gold. Carbon nanotubes and diamond nanoparticles have also been used in nanofluids. The base fluid is usually a conventional heat transfer fluid, such as oil, water, and ethylene glycol. Other base fluids are bio-fluids, polymer solutions and some lubricants.

A comprehensive survey of convective transport in nanofluids was made by Buongiorno (2006). He developed a non-homogeneous equilibrium model for convective transport to explain the enhanced heat transfer characteristics of nanofluids, and this abnormal increase in the thermal conductivity occurs due to the presence of two main velocity-slip effects, namely, the Brownian diffusion and the thermophoretic diffusion of the nanoparticles. In a recent paper, Khan and Pop (2010) have used the model of Kuznetsov and Nield (2010) to study the fundamental work on the boundary layer flow of nanofluid over a stretching sheet. Makinde and Aziz (2011) extended the work of Khan and Pop (2010) for convective boundary conditions. Ma et al. (2012) have developed a hybrid approach that combines the Lattice Boltzmann model for fluid with a Brownian dynamics model for the nanoparticles.

It is now a well-accepted fact that many fluids of industrial and geophysical importance are non-Newtonian. Due to much attention in many industrial applications, such as the extrusion of plastic sheets, fabrication of adhesive tapes, glass-fiber production, metal spinning, drawing of paper films, the research on boundary layer behaviour of a viscoelastic fluid over a continuously stretching surface keeps going where the velocity of a stretching surface is assumed linearly proportional to the distance from a fixed origin. McCormack and Crane (1973) have provided comprehensive discussion on boundary layer flow caused by stretching of an elastic flat sheet moving in its own plane with a velocity varying linearly with distance. Several researchers viz., Gupta and Gupta (1977); Dutta et al. (1985); Chen and Char (1988) extended the work of Crane (1973) by including the effects of heat and mass transfer under different situations. Later on, Rajagopal et al. (1984), Chang (1989) presented an analysis on flow of viscoelastic fluid over a stretching sheet. The above sources all utilize the no-slip condition. On the other hand, in certain circumstances, the partial slip between the fluid and the moving surface may occur in situations when the fluid is particulate such as emulsions, suspensions, foam and polymer solutions. In these cases, the proper boundary condition is replaced by Navier’s condition, where the amount of relative slip is proportional to local shear stress. Wang (Wang 2002) discussed the partial slip effects on the planar stretching flow. Of late, Noghrehabadi et al. (2012) investigated the development of the slip effects on the boundary layer flow and heat transfer over a stretching sheet. Surana et al. (2012) have used K-version finite element method to solve the viscoelastic flow through the parallel plates.

In real situations in nanofluids, the base fluid does not satisfy the properties of Newtonian fluids, hence it is more justified to consider them as viscoelastic fluids, e.g., Ethylene glycol–Al₂O₃, Ethylene glycol–CuO and Ethylene glycol–ZnO are some examples of viscoelastic nanofluids. In the present paper, the base fluid is taken as a second grade fluid. To the best of our knowledge, no studies so far have been investigated to analyze the partial slip effect on the boundary layer flow of viscoelastic nanofluid over a stretching sheet. The objective of the present paper is therefore to extend the work of Noghrehabadi (2012) by taking the base fluid as a second grade fluid. The finite element method (FEM) is used in obtaining the numerical solution of the obtained equations, which describe the problem, after similarity transformation. A similarity solution is presented and used to predict the heat and mass transfer characteristics of the flow. The effects of the embedded flow controlling parameters on the fluid velocity, temperature, nanoparticle concentration, heat transfer rate, and the nanoparticle volume fraction rate have been demonstrated graphically and discussed. A comparative study is also presented.

Mathematical formulation

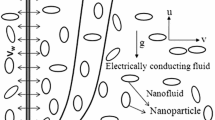
Consider two-dimensional, steady, incompressible, laminar flow of non-Newtonian nanofluid past a stretching sheet in a quiescent fluid. The velocity of the stretching sheet is $u_{\text{w}} = U = cx$ (where $c > 0$ is the constant acceleration parameter). The x axis is taken along the plate in the vertically upward direction and the y-axis is taken normal to the plate. The surface of plate is maintained at uniform temperature and concentration, $T_{\text{w}}$ and $C_{\text{w}}$, respectively, and these values are assumed to be greater than the ambient temperature and concentration, $T_{\infty }$ and$C_{\infty }$, respectively. Moreover, it is assumed that both the fluid phase and nanoparticles are in thermal equilibrium state. The thermo physical properties of the nanofluid are assumed to be constant. The pressure gradient and external forces are neglected.

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$

(1)

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \upsilon \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + \frac{{\alpha_{1} }}{{\rho_{\text{f}} }}\left[ {\frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial y^{2} }} + u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + \frac{\partial u}{\partial y}\frac{{\partial^{2} v}}{{\partial y^{2} }} + v\frac{{\partial^{3} u}}{{\partial y^{3} }}} \right] $$

(2)

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{m}} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \,\tau \left[ {D_{\text{B}} \frac{\partial C}{\partial y} \cdot \frac{\partial T}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] $$

(3)

$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }} \cdot \frac{{\partial^{2} T}}{{\partial y^{2} }} $$

(4)

The boundary conditions for the velocity, temperature, and concentration fields are given as follows:

$$ u = U + \kappa \upsilon \frac{{\partial u}}{{\partial y}},\,v = 0,\,T = T_{\rm{w}} ,\,C = C_{\rm{w}} \,\,{\text{at}}\,\,y = 0 $$

(5a)

$$ u = 0,\quad T = T_{\infty } , \quad C = C_{\infty } \quad as \quad y \to \infty $$

(5b)

where $u$ and $v$ are the velocity component along the $x$ and $y$ directions, respectively, $\rho_{f}$ is the density of base fluid, $\mu$ is the absolute viscosity of the base fluid, $\upsilon$ is the dynamic viscosity of the base fluid, $\alpha_{1}$ is the material fluid parameter, $T$is the fluid temperature, $\alpha_{\text{m}}$is the thermal diffusivity, $\tau \left( { = \left( {\rho C} \right)_{\text{p}} /\left( {\rho C} \right)_{\text{f}} } \right)$is the ratio of effective heat capacity of the nanoparticle material to heat capacity of the fluid, $\rho_{\text{p}}$ is the nanoparticle density, $C$is the nanoparticle volume fraction, $D_{\text{B}}$ and $D_{\text{T}}$ are the Brownian diffusion coefficient and the thermophoresis diffusion coefficient, $T_{\infty }$is the free stream temperature, $C_{\text{p}}$is the specific heat at constant pressure.

To transform the governing equations into a set of similarity equations, the following dimensionless parameters are introduced:

$$ \eta = \sqrt {\frac{c}{\upsilon }} y,\quad u = cxf^{\prime}\left( \eta \right),\,v = - \sqrt {c\upsilon } f\left( \eta \right),\,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\quad \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }} $$

(6)

The transformed momentum, energy and concentration equations together with the boundary conditions given by (1–4), (5a, 5b) can be written as:

$$ f^{'''} + f^{''} - f^{'2} - \alpha \left( {f^{''2} - 2f^{'} f^{'''} + ff^{iv} } \right) = 0 $$

(7)

$$ \frac{1}{\Pr }\theta^{''} + f\theta^{'} + Nb\theta^{'} \phi^{'} + Nt\theta^{'2} = 0 $$

(8)

$$ \phi^{''} + Lef\phi^{'} + \frac{Nt}{Nb}\theta^{''} = 0 $$

(9)

The transformed boundary conditions are:

$$ f = 0,\,f^{'} = 1 + Kf^{''},\,\theta = 1,\,\phi = 1\,\,at\,\,\eta = 0 $$

(10a)

$$ f^{'} = 0,\,\theta = 0,\,\phi = 0\,\,as\,\,\eta \to \infty $$

(10b)

where primes denote differentiation with respect to $\eta$ and the seven parameters appearing in Eqs. (7–9) are defined as follows:

$$ \begin{gathered} \Pr = \frac{\upsilon }{{\alpha_{\text{m}} }},\,\,\,Le = \frac{\upsilon }{{D_{\text{B}} }},\,\alpha = \frac{{\alpha_{1} c}}{\mu }, \hfill \\ Nb = \frac{{\left( {\rho C} \right)_{\text{p}} D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}}{{\left( {\rho C} \right)_{\text{f}} \upsilon }},\,\,\,Nt = \frac{{\left( {\rho C} \right)_{\text{p}} D_{\text{T}} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\left( {\rho C} \right)_{\text{f}} T_{\infty } \upsilon }} \hfill \\ \end{gathered} $$

(11)

In Eq. (11), $Pr,\,Le,\,\alpha ,\,Nb$ and $Nt$ denote the Prandtl number, the Lewis number, the viscoelastic parameter, the Brownian motion parameter, and the thermophoresis parameter, respectively.

The physical quantities of interest are the local heat flux $Nu$ and the local mass diffusion flux $Sh$ from the vertical moving plate, which are defined as:

$$ Nu = \frac{{xq_{w} }}{{k\left( {T_{w} - T_{\infty } } \right)}},\,Sh = \frac{{xh_{w} }}{{D_{B} \left( {C_{w} - C_{\infty } } \right)}},\, $$

(12)

where $\tau_{w}$is the wall skin friction, $q_{w}$is the surface heat flux and $h_{w}$is the wall mass flux given by

$$ q_{w} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} ,\quad h_{w} = - D_{B} \left( {\frac{\partial C}{\partial y}} \right)_{y = 0} $$

(13)

Using (6) in (12), one can obtain

$$ \,\text{Re}_{x}^{ - 1/2} Nu_{x} = - \theta^{\prime}\left( 0 \right),\,\,\text{Re}_{x}^{ - 1/2} Sh_{x} = - \phi^{\prime}\left( 0 \right) $$

(14)

where $\text{Re}_{x} = u_{w} \left( x \right)x/\upsilon$ is the local Reynolds number based on the stretching velocity $u_{w} \left( x \right)$. Kuznetsov and Nield (2010) referred $\text{Re}_{x}^{ - 1/2} Nu_{x}$ and $\text{Re}_{x}^{ - 1/2} Sh_{x}$ as the reduced Nusselt number $Nur = - \theta^{\prime}\left( 0 \right)$ and reduced Sherwood number $Shr = - \phi^{\prime}\left( 0 \right)$, respectively. The analytical solutions of the set of partial differential equations given by (7–9) are generally intractable because these equations are highly non-linear. The variational finite element method (FEM) is used to obtain numerical solutions. These techniques have been used very successfully in non-linear magneto fluid dynamics.

Method of solution

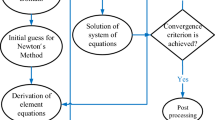
FEM is a numerical and computer-based technique of solving a variety of practical engineering problems that arise in different fields. It is recognized by developers and users as one of the most powerful numerical analysis tools ever devised to analyze complex problems of engineering. It has been applied to a number of physical problems, where the governing differential equations are available. The method essentially consists of assuming the piecewise continuous function for the solution and obtaining the parameters of the functions in a manner that reduces the error in the solution. The steps involved in the finite element analysis are as follows:

• Discretization of the domain into set of finite elements.

• Weighted integral formulation of the differential equation.

• Defining an approximate solution over the element.

• Substitution of the approximate solution and the generation of the element equations.

• Assembly of the stiffness matrices for each element.

• Imposition of the boundary conditions.

• Solution of assembled equations.

The entire flow domain is divided into 10,000 quadratic elements of equal size. Each element is three-noded, and therefore, the whole domain contains 20,001 nodes. At each node four functions are to be evaluated; hence after assembly of the element equations, we obtain a system of 80,004 equations which are non-linear. Therefore, an iterative scheme must be utilized in the solution. After imposing the boundary conditions, a system of equations has been obtained which is solved by the Gauss elimination method. The code of the algorithm has been executed in MATLAB running on a PC. Excellent convergence was achieved for all the results.

Result and discussion

The non-linear ordinary differential equations (7–9) together with the boundary conditions (10a, 10b) are solved numerically using FEM. The numerical computations have been carried out for different values of the parameters involved, namely, viscoelastic parameter α, Prandtl number Pr, slip parameter K, Lewis number Le, the Brownian motion parameter Nb and thermophoresis parameter Nt. The effects of the flow controlling parameters on the dimensionless axial velocity, temperature, the nanoparticle volume fraction, the rate of heat and mass transfer are investigated and presented graphically in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The aim of the present study is to examine the variations of different quantities of parameters in which $\,0 \le K \le 10,\,\,\,0 \le \alpha \le 10,\,\,\,\,0 \le Pr \le 70,\,\,\,\,0.1 \le Nt \le 0.5,\,$$\,0.1 \le Nb \le 0.5,\,$ and $5 \le Le \le 30$. The computational work is carried out by taking size of the element$\nabla \eta = 0.0001$. The accuracy of current solutions is independent with the size of the element, thus the results are convergence solutions.

Fig. 1

Velocity profile for various values of $K$ when $Pr = Le = 10,Nb = Nt = 0.1,\,\alpha = 0.5$

Fig. 2

Temperature profile for various values of $K$ when $Pr = Le = 10,Nb = Nt = 0.1,\,\alpha = 0.5$

Fig. 3

Concentration profile for various values of $K$ when $Pr = Le = 10,Nb = Nt = 0.1,\,\alpha = 0.5$

Fig. 4

Velocity profile for various values of $\alpha$ when $Pr = Le = 10,Nb = Nt = 0.1,\,K = 1.0$

Fig. 5

Temperature profile for various values of $\alpha$ when $Pr = Le = 10,Nb = Nt = 0.1,\,K = 1.0$

Fig. 6

Concentration profile for various values of $\alpha$ when $Nb = Nt = 0.1,\,Pr = Le = 10,K = 1.0$

Fig. 7

Temperature profile for various values of $Nt$ when $Pr = Le = 10,Nb = 0.1,\,K = 1.0,\alpha = 0.5$

Fig. 8

Concentration profile for various values of $Le$ when $K = 1.0,\alpha = 0.5Nb = Nt = 0.1,\,$$Pr = 10,$

Fig. 9

Effect of $Nt$ and $\alpha$ on reduced Nusselt number for $Pr = Le = 10,\,\,Nb = 0.1,\,K = 1.0$

Fig. 10

Effect of $Nt$ and $\alpha$ on reduced Sherwood number for $Pr = Le = 10,\,\,Nb = 0.1,\,K = 1.0$

Figures 1, 2, 3 illustrate the velocity, temperature and concentration profiles for different values of the slip parameter K. Figure 1 demonstrates that the effect of increasing value of slip parameter K is to shift the streamlines toward stretching boundary and thereby reduce thickness of the momentum boundary layer. Therefore, the effect of slip parameter K is seen to decrease the boundary layer velocity while the temperature and concentration are increased with the increase of the slip parameter. The velocity curves show that the rate of transport decreases with the increasing distance $\left( \eta \right)$ normal to the sheet. In all cases the velocity vanishes at some large distance from the sheet (at $\eta = 6$).

Figures 4, 5, 6, show the effect of viscoelastic parameter α on the evolution of fluid motion and subsequent on the distribution of heat and mass across the sheet as time evolves. From this plot it is evident that increasing values of viscoelastic parameter α opposes the motion of the liquid close to the stretching sheet and assists the motion of the liquid far away from the stretching sheet. Increasing values of second-grade parameter enables the liquid to flow at a faster rate due to which there is decline in the heat transfer. This is responsible for the increase in momentum boundary layer whereas the thermal and concentration boundary layers reduce when the viscoelastic effects intensify. Figure 7 illustrates the temperature profile for different values of thermophoretic parameter Nt and the effect of Lewis number Le on the concentration profile are shown in Fig. 8.

In order to understand the influence of thermophoresis parameter Nt on heat and mass transfer the local Nusselt and Sherwood number are plotted in Figs. 9, 10 for different values of viscoelastic parameter α. From the earlier graphical results, we have noticed that the thickness of the thermal and concentration boundary layers reduce when the viscoelastic effects intensify. This reduction is compensated with the increase in the rate of heat and mass transfer at the stretching surface. Also, the profiles obtained from these Figures of reduced Nusselt and Sherwood numbers are compared with those reported by Noghrehabadi et al. (2012) in case of α=0.

In the present study, the local rate of heat transfer (reduced Nusselt number Nur) and local rate of mass transfer at the sheet (reduced Sherwood number Shr), defined in equation (14), are the important characteristics. The numerical values of reduced Nusselt number and reduced Sherwood number are exhibited in Tables 1, 2, 3, 4. Table 1 shows that the excellent correlation between the current FEM computations and the earlier results of Wang (1989), Gorla and Sidawi (1994), for reduced Nusselt number ($- \theta^{\prime}(0)$) by neglecting slip effect (K), the viscoelastic parameter (α), Brownian effect (Nb) and thermophoresis (Nt) for various values of Prandtl number (Pr) with step size, h = 0.0003. Variations of reduced Nusselt number Nur and reduced Sherwood number Shr with Nt are depicted in Table 2. Further for various values of Nt and Nb, the results are compared with those reported by Khan and Pop (2010), Noghrehabadi et al. (2012) and the comparison are found to be in good agreement for each value of Nt and Nb, which confirm that the present results are accurate. The values of $- \theta^{\prime}\left( 0 \right)$and$- \phi^{\prime}\left( 0 \right)$are compared with analytical values, for the accuracy of the solution, reported by Noghrehabadi et al. (2012) in Table 3. The variations in the numerical values of Nur and Shr are provided in Table 4 for various values of Nt and Nb and K when $Pr = Le = 10,\alpha = 0.5.$ It is observed that the reduced Nusselt number is a decreasing function, while the reduced Sherwood number is an increasing function of Nt

Table 1 Comparison of result for reduced Nusselt number $- \theta^{\prime}\left( 0 \right)$ for $Le = 10;\,\,\,Nb = Nt = 10^{ - 6} ;\,\,\,K = \alpha = 0$

Table 2 Comparison of $Nur$ and $Shr$ with $Nt$ for $\Pr = Le = 10;\,\,\,Nb = 0.1;\,\,\,K = 0;\,\,\,\alpha = 0$

Table 3 Comparison of $Nur$ and $Shr$ with $Nt$ for $\Pr = Le = 10;\,\,K = 1;\,\,\,\alpha = 0$

Table 4 Variation of$Nur$ and $Shr$ with $Nb,Nt$ and $K$ when $Le = Pr = 10$and $\alpha = 0.5$

Conclusion

The problem of boundary-layer flow of a viscoelastic nanofluid past a stretching sheet has been solved numerically to exhibit the effect of partial slip (i.e., Navier’s condition) on the fluid flow and heat transfer characteristics. By using a similarity transformation, the conservative equations for mass, momentum, energy, and nanoparticle concentration are transformed into the ordinary differential equations. We used the finite element method (FEM) for the numerical solution of these equations. The effects of different controlling parameters on the flow field and heat transfer characteristics are examined. The variation of the reduced Nusselt and Sherwood numbers with Nt for various values of α and K is presented in graphical form. The result can be summarized as follows:

• 1. With the increase in the second grade parameter α, the velocity and the momentum boundary layer thickness increase; however, the temperature and nanoparticles concentration decrease.

• 2. There is a decrease in the velocity, but temperature and concentration are found to increase with an increase in velocity slip parameter K.

• 3. With increase in the slip parameter K, heat transfer rate and mass transfer rate decrease.

• 4. By the increase of thermophoretic number Nt, the effect of velocity slip parameter K on reduced Nusselt number Nur and reduced Sherwood number Shr increases and decreases, respectively.

• 5. The reduced Nusselt number and reduced Sherwood number both increase with the increase of viscoelastic parameter α.