Gas sensing of Au/n-SnO₂/p-PSi/c-Si heterojunction devices prepared by rapid thermal oxidation

Abstract

Transparent and conducting SnO₂ thin film has been produced on (quartz, ITO, silicon and porous silicon) substrates using rapid photothermal oxidation of pure Sn in air at 600 °C oxidation temperature and different oxidation time. The structural, optical, electrical properties, scan electron microscope and atomic force microscope of the prepared films were studied. The transmittance T in the visible and NIR was investigated; the allowed direct energy gap was determined to be 3.18 eV at optimum condition of 600 °C and 90 s. The dependence of the resistivity on the film thickness and oxidation time has been studied. The optimum thickness of high transmittance and lowest resistivity is about 150 nm for SnO₂, where ρ = 1.7 × 10⁻³ Ω cm and T = 88 %. The sensitivity behaviors of the n-SnO₂/p-PSi/c-Si-based gas sensor to H₂ and CO₂ gas were investigated. The film sensitivity dependence on the temperature and test gas concentration was tested and the optimum operation temperature was determined at around 250 and 300 °C with an applied voltage was constant at 2.5 V.

Introduction

When a polycrystalline tin oxide (SnO₂) semiconductor thin film is exposed to air, physisorbed oxygen molecules pick up electrons from the conduction band of SnO₂ and change to ${\text{O}}^{ - }_{{ 2\left( {\text{ads}} \right)}}$ or ${\text{O}}^{ - }_{{\left( {\text{ads}} \right)}}$ species (Seal and Shukla 2002). Consequently, a positive space-charge layer forms just below the surface of SnO₂ particles, which creates a potential barrier between the particles increasing the electrical resistance of the SnO₂ film. However, when a reducing gas comes in contact with the film, it gets oxidized via reaction with the ${\text{O}}^{ - }_{{ 2\left( {\text{ads}} \right)}}$ or ${\text{O}}^{ - }_{{\left( {\text{ads}} \right)}}$ species and subsequently electrons are reintroduced into the electron depletion layer, leading to decrease in the potential barrier. The sensitivity of the SnO₂ thin film is usually determined by the ratio (Ra − Rg)/Rg (or Ra/Rg), where Ra and Rg are the resistances of the sensor in air and reducing gas, respectively. SnO₂-based gas sensor has been synthesized in various forms such as thin (Park and Mackenzie 1996; Sakai et al. 2001; Baik et al. 2000; Choi et al. 1997; Song et al. 1998; Cha et al. 1994; Sberveglieri et al. 1992; Michel et al. 1998; Malyshev et al. 1992) or thick films (Mishra and Agarwal 1994; Devi et al. 1999; Shimizu et al. 1993; Katsuki and Fukui 1998) and pellets (Jayaraman et al. 1999; Chaudhary et al. 1998, 1999). Thin films are synthesized using sols, which are prepared using either alkoxide (Park and Mackenzie 1996) or chloride (Sakai et al. 2001) precursors utilizing either dip (Park and Mackenzie 1996) or spin (Sakai et al. 2001) coating methods. Synthesis of SnO₂ thin films using hydrothermally treated sol (Sakai et al. 2001; Baik et al. 2000) and other conventional techniques such as ion-assisted deposition (Choi et al. 1997; Song et al. 1998), sputtering (Cha et al. 1994; Malyshev et al. 1992), evaporation (Carbajal et al. 2000), chemical vapor deposition (Brown et al. 2000), spray pyrolysis (Niranjan et al. 2002) have been reported. On the other hand, thick films are processed using a paste (Mishra and Agarwal 1994; Devi et al. 1999; Shimizu et al. 1993; Katsuki and Fukui 1998) prepared by mixing SnO₂ powder and a binder in a suitable solvent such as water or acetone, which is then applied using screen printing technology (Mishra and Agarwal 1994) on a suitable substrate. Mixing SnO₂ powder with polyvinyl alcohol (PVA) polymer and then pressing the mixed powders into a pellet, which is subsequently sintered at higher temperature, forms pellets (Jayaraman et al. 1999; Chaudhary et al. 1998, 1999). However, a lack of consistency in the sensor properties has been a major problem associated with all these techniques. The processing of SnO₂ semiconductor gas sensor based on pellets or thick film technology are practically excluded from integration in the fabrication of intelligent microsystems, not only due to processing incompatibility but also due to the high power consumption for the gas-sensing applications. Thin film technology based on physical methods like vacuum evaporation or sputtering for SnO₂ deposition, combined with ion-implantation for doping the films with metal ions, is very expensive and may suffer composition inhomogeneity and poor capability to provide good step coverage for topographies with very high aspect ratios. On the other hand, it is well known that the sol–gel technique (used for thin films) has several advantages such as easy control of film thickness, low-cost processing, and ability to produce ultrafine particles, and to coat large complex shapes (Klein 1988). The gas-sensing properties of SnO₂ semiconductor thin film has been found to depend strongly on the method of processing. Among the structural parameters, the nanocrystallite size (Seal and Shukla 2002) and the film thickness (Park and Mackenzie 1996) have pronounced effect on the gas sensitivity. It is now recognized that SnO₂ semiconductor thin film can have maximum gas sensitivity only if the nanocrystallite size within the film is comparable with its space-charge layer thickness (Seal and Shukla 2002). Hence, the major objectives of the present investigation are set to synthesize SnO semiconductor thin film, having nano-sized crystallites (critical parameters for achieving maximum sensitivity) using the rapid thermal oxidation technique. Various analytical techniques such as scanning electron microscopy (SEM), X-ray diffraction (XRD), atomic force microscopy (AFM) and optical properties are utilized in the present investigation. Besides, the present study also focuses on demonstrating the suitability of such SnO₂/PSi/c-Si device for sensing H₂, CO₂ gas.

Experimental work

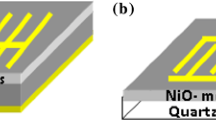
High purity of tin (Sn) thin film was deposited on (quartz, ITO glass, p-type silicon and p-type PSi single crystal (111) silicon substrates) using thermal evaporation technique at room temperature under a vacuum pressure of 10⁻⁶ Torr. Electrochemical anodization was performed in dark to produce porous Si layers on polished p-type, single crystal (111) oriented Si wafers with a resistivity of 0.01–0.02 Ω cm and a thickness of ~508 ± 5 μm, using a 1:4 mixture of 48 % HF: 98 % ethanol as an electrolyte. Initially, the Si wafers were cleaned successively in a sonicating bath with CCl₄, toluene, acetone, ethyl alcohol and 18.5 M cm deionized water. The anodization was carried out with the distance between the Si substrate to the Pt counter electrode fixed at ~2.5 cm, using a current density of 40 mA/cm² for a fixed time of 5 min. The wafer and platinum cathode were placed in a Teflon jig, schematically illustrated in Fig. 1a. The surfaces of Si substrate and Pt cathode were kept parallel to each other and the current flow in the etchant was normal to the wafer surface. After the anodization, the PSi layers were dried in the following way to reduce the capillary stress using pentane, which has very low surface tension and no chemical reactivity with the PSi layer. The samples were rinsed first with pentane, then with 98 % methanol and finally with deionized water (18.5 M cm). Next, the samples were dried at about 60 °C on a hot plate rather than drying in the N₂ nozzle to avoid cracking and peeling of the PSi layer.

Fig. 1

a Schematic illustration of the porous silicon etching setup and b rapid photo-thermal oxidation (RTO) setup and c a schematic diagram of the IDE masks utilized in this work

The resistivity and type of conductivity of the Si substrates were measured using four-point probe (FPP) technique. SnO₂ film was obtained with the aid of rapid photo-thermal oxidation system with halogen lamp as oxidation source. The oxidation condition used to form SnO₂ film was 600 °C and different oxidation times. Figure 1b shows the system used to prepare the oxide film; where a quartz tube of 3 cm diameter with two open ends was used to ensure the flow of air through it. The source of dry oxygen was used. 650-W halogen lamps were used to provide light and heat radiation and a variable power supply to control the output power. A k-type thermocouple was used to monitor samples temperature. The silicon sample was used as substrate for TCO’s/PSi heterojunction. Ohmic contacts were fabricated by evaporating 99.999 purity aluminum wires for back contact, and 99.999 pure gold were used as front contact through special mask using Edwards coating system. A boat of tungsten was used to include the evaporated source. Figure 1c illustrates two 8- and 10-finger interdigitated electrode IDE metal masks which were utilized in this work. The samples were fixed in the evaporation system.

Results and discussion

XRD-diffraction

The structure and lattice parameters of SnO₂ films were analyzed by a LabX XRD 6000 SHIMADZU XR-diffractometer with Cu Kα radiation of (voltage 30 kV, current 15 mA, scanning speed = 4°/min). Figure 2 shows the diffraction pattern for samples prepared at oxidation temperature 600 °C and different oxidation time. The XRD patterns at oxidation time of 60 s are shown in Fig. 2a. It shows that the peaks appeared at 2θ = 33.8436° and 2θ = 34.0896° are corresponding to the diffraction from (101) planes which are related to the formation of SnO₂ films. At 90 s oxidation time and 600 °C oxidation temperature, Fig. 2b shows that the structures of films are clearly improved where a significant increase in peak intensity at (101) plane can be attributed to the improvement in the structural order, which can also be attributed to the increase in the SnO₂ film density, resulting in the demonstration of the (101) SnO₂ peak rather than the other peak. This indicates the formation of nearly stoichiometry SnO₂ films. The intensities of these peaks reduce with the increasing of oxidation time up to 120 s as shown in Fig. 2c. The results below ensure that the optimum value of oxidation temperature is 600 °C and oxidation time is 90 s. The deviation in XRD peak of the film with respect to the standard ASTM data is attributed to the mechanical micro-stress produced by different sources like impurities, defects and vacancies reside in the film structure. Results at higher oxidation time 140 s and at the same oxidation temperature are shown in Fig. 2d, which recognizes the peaks at 2θ = 33.9813° in the spectra of SnO₂ film corresponding to the reflection from (101) plane. The presence of sharp peak (in all deprogram) indicates that all films are polycrystalline in nature with a tetragonal structure and in accordance with data reported in literature (Gordillo et al. 1994; Choe et al. 1999; Mitchell 2004). Table 1 shows the effect of oxidation times on the XRD characteristics evaluated from the diffrograms. In the case of tetragonal structure which is the ruling form for SnO₂ thin films, the lattice constants are a = b ≠ c as shown in Table 2. These constants change with structural change caused by the different parameters such as deposition technique, doping, substrate, etc., and the lattice constant can be found by measuring different values of (d) not less than two or three or four times of X-ray spectrum using the formula (Mosadegh Sedghi and Vesali Naseh 2009):

Fig. 2

X-Ray diffraction patterns for SnO₂ thin films prepared at different oxidation time and 600 °C

Table 1 XRD patterns characteristics of SnO₂ films at various oxidation times

Table 2 Lattice constants as a function of oxidation temperature and oxidation time of SnO₂ thin film

$$ \frac{1}{{d^{2} }} = \frac{{(h^{2} + k^{2} )}}{{a^{2} }} + \frac{{l^{2} }}{{c^{2} }} $$

(1)

where h, k, l are the Miller indices of the lattice plane. The values of lattice constants for SnO₂ films prepared at different oxidation temperature and oxidation time have been listed in Table 2. The grain size (D) is calculated using the Scherrer formula from the full-width half-maximum (FWHM) (β) (Van and Dinh 1998):

$$ D = \frac{K\lambda }{\beta \cos\theta } $$

(2)

where λ is the wavelength of the X-ray used, β is the FWHM, D is the grain size value and θ is half the angle between incident and the scattered X-ray beams. The (D) values are listed in the Table 3. It shows that grain size of the films is increased with increasing of oxidation time up to (90 s).The intense and sharp peaks in XRD pattern reveal the good crystallinity of the films and also confirm the stoichiometric nature of SnO₂ films.

Table 3 Grain size of SnO₂ thin film

Scan electron microscope (SEM)

Surface morphologies obtained through SEM study carried out by (Hitachi FE-SEM model S-4160, Japan) in University of Tehran at 15 kV of SnO₂ films prepared at oxidation temperature 600 °C and different oxidation times. SEM micrograph shows that surface of SnO₂ thin films are smoother as shown in Fig. 3a–d. The films consist of small particles distributed on the surface that shows nanostructure properties. The structure is polycrystalline with very fine pores distributed fairly uniformly on the film surface. We can observe a dense granular structure. The grains have different shapes and sizes. The grain size found using SEM is smaller than those derived from X-ray diffraction. From SEM observations given by Fig. 3, we note that the average grain size is comparable to the film thickness which is <100 nm.

Fig. 3

Scanning electron microscope of SnO₂ film prepared at 600 °C and oxidation time a 60 s, b 90 s, c 120 s and, d 140 s

Atomic force microscope (AFM)

It is known that the surface properties of the transparent conducting oxide films influence their optical and electrical properties which are important factors for applications in optoelectronic devices; in principle, the increase in surface roughness of the films leads to a decrease in the efficiency for photovoltaic properties, therefore, it is very important to investigate the surface morphology of the films (Van and Dinh 1998). The AFM technique uses a laterally moving tip, while the cantilever reflects the sample’s topography, or the Z measurements. Even though the tip is very sharp, it is impossible to gather the information from the underside of specimen. The spherical particle will be viewed as a bump by the atomic force microscope. To correct the AFM image for this effect some deconvolution techniques are used. The surface morphology of Ag₂O films as observed from the (AFM-AA3000, Angstrom Advanced Inc., USA) micrographs proves that the grains are uniformly distributed within the scanning area (1,000 × 1,000 nm) with individual columnar grains extending upwards as shown in Fig. 4. The grain size decreases with the oxidation time increases, while the films presented uniformity. Since the size grain decreases in dimension when the film thickness decreases, it suggests that the charge transport is occurring predominantly intra-grain in cases of lower thickness, or equivalent to greater grains, and that there is a preferential charge transport inter-grain in greater thickness samples, where there are more the interface grains, in this kind of microstructure it is usually not dominated by bulk properties but by grain walls, which either act as low conductivity blockades or as high conductivity carrier accumulation regions. This surface characteristic is important for applications such as solar cells, gas sensors and catalysts (Gyogy and Axente 2000; Al-Hardan and Abdulllah 2009). The root mean square (rms) roughness of the film surface roughness was prepared at different conditions as listed in Table 4.

Fig. 4

AFM images of SnO₂ prepared at 600 °C and different oxidation times a 60 s, b 90 s, c 120 s and d 140 s

Table 4 The grain size of SnO₂ film prepared at different oxidation time and oxidation temperature 600 °C

Optical properties

Figure 5 shows the optical transmission (200–1,000) nm as a function of the wavelength for SnO₂ film prepared at different oxidation time and constant oxidation temperature; high transmission (>90 %) was exhibited by films prepared at 120 and 140 s oxidation time, may be because the increase in the oxidation leads to large molecular symmetry (stoichiometry) where (101) SnO₂ films are demonstrated over all other oxide film peaks.

Fig. 5

Optical transmission as a function of wavelength for SnO₂ thin films prepared on quartz substrate different oxidation time

In general, it has been found that the transmission of the films was increased when the oxidation temperature was increased due to film transformation from metal to transparent oxide. The optical band gap was calculated for films prepared at optimum oxidation time and temperature. The band gaps of these films were calculated from Fig. 6 using the formula (Kuku Titilayo 1986):

Fig. 6

Energy band gap of the SnO₂ at oxidation temperature (600 °C) and oxidation time (90 s)

$$ \alpha h\nu = A(h\nu - E_{g} )^{m} $$

(3)

where α = absorption coefficient, h = Planck’s constant, υ = frequency of incident light, E_g = band gap of the material, m = factor governing the direct/indirect, etc. transitions of the electrons from the valence band to the conduction band.

The plots of (αhυ)² against hυ for SnO₂ film prepared at (600 °C) and (90 s) is shown in Fig. 6. The nature of the plot suggests a direct inter-band transition. The extrapolation of the straight-line portion to zero absorption coefficient (α = 0) leads to the estimation of band gap energy, this band gap found to be about 3.54 eV. This result is conditional with many other workers (Roman 2006; Yadav et al. 2007; Mohammed Khalid 2005).

The dependences of absorption coefficients α on photon energy are represented in Fig. 7 for the film grown at different oxidation time. The direct optical band gap increases to give a blue shift. This shift is due to increase in carrier concentration which results in filling the bottom of the conduction band and this filling prevents the transition of the photogenerated carriers into the filled levels according to quantum rules and hence leads to far transitions with larger photon energy. This shift is called Burstein–Moss effect. The E_g is found to be about 3.5–3.7 eV at T = 600 °C, and different oxidation times are shown in Fig. 8. These results agree with published literatures (Zhu and Yao 2006).

Fig. 7

α (cm⁻¹) vs. hυ of SnO₂ films at different oxidation time

Fig. 8

(αhυ)² (eV/cm)² vs. hυ of SnO₂ films at different oxidation time

Electrical properties

The logarithmic conductivity as a function of temperature for SnO₂ oxide samples prepared at the optimum condition is given in Fig. 9. It is clear that the values of conductivity increase with temperature, such as the general characteristics of the semiconductor with increasing temperature lead to an increase in the number of electron-holes pairs resulting on increased conductivity. The linear proportionality in the curve is related to the increase in the number of ionized carriers from the valance band to the conduction band as the substrate is heated.

Fig. 9

Electrical conductivity vs. 1,000/T

The value of the activation energy has been estimated using the following equation (Yoshiaki 2003):

$$ \sigma_{dc} = \sigma_{o} { \exp }\left( {\frac{{ - E_{a} }}{kT}} \right) $$

(4)

where σ_o is the high temperature limit of conductivity, E_a is activation energy and kT is the thermal energy associated with temperature variation in the measurement, where k is Boltzman constant and T is absolute temperature (Table 5).

Table 5 Activation energy of SnO₂ film prepared at different oxidation time and oxidation temperature 600 °C

The variation in the resistivity with oxidation times for SnO₂ film is shown in Fig. 10. The decrease in resistivity may be due to the conversion of SnO to SnO₂ so that the SnO concentration is decreased, leading to an increased conductivity due to the filling of the oxygen vacancies in SnO₂ and hence the oxygen-deficient SnO₂ would become nearly stoichiometric and insulating. The minimum resistivity of the SnO₂ films obtained in this work is about 1.7 × 10⁻³ Ω cm, and this agrees with the result in similar work (Gordillo et al. 1994; Raviendra and Sharma 1985).

Fig. 10

Resistivity as a function of oxidation times for SnO₂ thin film

The conductivity type of SnO₂ films was determined by Hall effects. Table 6 shows that the results indicate that the materials under study are n-type semiconductors possibly due to the donor formation by O₂ vacancies; these results agree with the results of Zhang and Tian (2011).

Table 6 Hall coefficient of SnO₂ film prepared at different oxidation time and oxidation temperature 600 °C

The carrier concentration and Hall mobility as a function of oxidation times are demonstrated in Fig. 11. The carrier concentration increases up to oxidation time 60 s. The variation of carrier concentrations can ascribe to the generation of conduction electrons and, thus, increasing the carrier concentration. The mobility of SnO₂ films shows a continuous decrease as the increasing of oxidation times. The actual value of mobility is determined by the interaction between the various scattering centers and free carriers. This result in a good agreement with that obtained by Zhang and Tian (2011a, b).

Fig. 11

The variation of carrier concentration and hall mobility with doping concentration of SnO2:Pd films

Scan electron microscope (SEM) for porous silicon

The SEM study was carried out by (VEGA TESCAN-SEM) in University of Technology, Baghdad, Iraq at 20 kV. The reproducibility of structural and optical properties of porous silicon is a fundamental issue (Pascual et al. 2002) that helps in device fabrication related to PSi. In this work, we stick to the optimum experimental parameters in respect of the PSi preparation with desired reproducibility. The porosity (gravimetric) values of the PSi layers formed on p-type Si wafers (henceforth, called as p-PSi, respectively) were 85 %, respectively, for an etching time of 5 min using Eq. (3). An estimation of the porosity is obtained gravimetrically: first, the weight of the virgin wafer is measured before anodization (M₁), then after anodization (M₂), and finally after dissolution of the porous silicon layer (M₃) in a 1 M solution of sodium hydroxide (NaOH). After determining these values, the porosity is given by the following equation (Bisi et al. 2000):

$$ {\text{Porosity}}\,\% = \frac{{M_{1} - M_{2} }}{{M_{1} - M_{3} }} $$

(5)

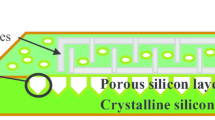
The etching time has been fixed at 5 min with the current density of 40 mA/cm² as an optimum condition, since the reproducibility of porosity values lies within 2–3 %. It is well known that PSi can exist in different microstructural forms depending upon various electrochemical parameters, silicon doping and resistivity (Kocka et al. 1995). According to IUPAC classification of pore size, our PSi samples should belong to either the mesoporous (2–50 nm) or the nanoporous (<2 nm) region as evident from the plan-view SEM micrograph (Fig. 12a). As expected, the PSi surface p-type Si wafers are characterized by the presence of large number of pores, more or less, regular in size.

It is established (Gaburro et al. 2000) that the higher thickness of porous silicon poses the danger of a bad electrical contact on the PSi device, resulting in the worst efficiency characteristics, although it helps in improving the power efficiency. The thickness values of the PSi layers formed on p-type Si wafers (henceforth, called as p-PSi, respectively) were 50.78 μm, respectively, for an etching time of 5 min using Eq. (4). The thickness of the layers is another important parameter that is closely related to the etching parameters of anodization time and hydrofluoric acid concentration. Similar to porosity, the thickness can be approximated gravimetrically by the following equation:

$$ T_{\text{PSi}} = K* J^{m} *t $$

(6)

where T_PSi in (cm), J = etching current density (mA/cm²), t = etching time (s). Constants K and m are tabulated in Table 7 and depend on HF concentration. Another way to measure the film thickness is by direct determination using the SEM or AFM (Berger et al. 2001).

Table 7 Coefficient determined for the empirical Eq. 7

Figure 12a shows the topography of the porous silicon formed by the electrochemical anodization process of monocrystalline silicon in HF-based solution at 40 mA/cm² for 5 min in dark and white at room temperature. As shown, a nearly uniform distribution of pores and a sponge-like structure of the porous layer are obtained. The porosity and thickness of porous silicon is a major concern of researchers in the field. However, understanding how to control PSi morphology is extremely difficult owing to the large number of controlling factors (Gaburro et al. 2000; Berger et al. 2001). The morphology of PSi is also strongly affected by the etching current density. The silicon dissolution process requires the presence of fluorine ions (F⁻) and holes (h⁺). As shown in Fig. 12b, when the fluorine ions are delivered faster than the holes, the inter-pore regions of PSi are depleted of holes; and further etching occurs only at the pore tips, where the holes are focused by the electric field. When the current density decreases, the number of holes at the pore tips drops, which lead to smaller pore sizes. Thus, the porosity (defined as the percentage of void space in the material) can be precisely controlled by the etching current density.

Fig. 12

SEM micrograph of PSi prepared with J = 40 mA/cm² at t = 5 min. a p-type porous silicon, and b schematic of PSi formation. Etching occurs only at the pore tips where the holes (h⁺) are focused by the electric field

Atomic force microscope for tin oxide/porous silicon

The surface morphology of as deposited tin thin metal film on the porous silicon substrate before any heat treatment revealed as shown in Fig. 13a, that the poured structure was destroyed; this is related to the thin film growth mechanism.

Fig. 13

Surface morphology of a deposited tin thin film (Sn)/p-PSi/c-Si and Au/n-SnO₂/p-PSi/c-Si oxidized at 600 °C

By rapid thermal oxidation at 600 °C oxidation temperature and 90 s oxidation time (Fig. 13b), a re-crystallization of the deposited atom above the nano-crystalline silicon substrate begins to take place and at the same time the surface morphology of the porous silicon itself changed due to the formation of nano silicon dioxide (SiO₂) and the reduction in porous silicon grain size and roughness. The result shows a uniform net work-like porous surface with a root mean square value (39.1 nm) that revealed low roughnesses of about (30.6 nm) which insure homogeneity in pore size values, comparing with Fig. 13a where the RMS was (33.2 nm) and the roughness about (23.8) the increase in its value on first case related to the re-distribution of oxide atoms on the porous surface and also associated with the increase in the average grain size (from 216.41 to 222.32 nm). The obtained films display smooth, uniform grain size and void free, i.e., very limited no. of droplets was observed.

XRD for tin oxide/porous silicon

XRD is a convenient method to evaluate the degree of crystallinity in PSi, although it is less direct than electron microscopy techniques. Figure 14 shows the XRD pattern of non-etched silicon (fresh silicon); it is clear that just one sharp and high-intensity diffracted peak noticed at 2θ = 28.3212 corresponds to (111) plane. This peak can be indexed as single crystal silicon cubic phase. The lattice constant of silicon is calculated and found 0.5364 nm which is very close to powder ASTM data (0.54 nm). The FWHM value of the diffracted silicon peak is 0.16960. XRD studies of porous silicon show distinct variations between the fresh silicon surface and the porous silicon surfaces formed at 40 mA/cm² anodizing current density and 5 min anodizing time.

Fig. 14

X-Ray diffraction patterns for a silicon substrate, and b Au/n-SnO₂/p-PSi/c-Si

The XRD pattern of SnO₂ film deposited on porous silicon prepared at 40 mA/cm² is depicted in Fig. 14. Four diffracted peaks are observed at 2θ = 26.657°, 33.865°, 38.053°, 47.113°, 54.685° and 57.947°, corresponds to (110), (101), (200), (022), (220) and (002) planes. These peaks belong to polycrystalline SnO₂ film with tetragonal phase. The FWHMs of these four peaks are broader than that for SnO₂ film deposited on quartz substrate, while their intensities are smaller. During the growth of SnO₂ on PSi (here, nanocrystallites of Si), the SnO₂/Si interface has determined the favorable orientation for SnO₂: (110) or (101) or (200) or (022) or (220) and (002). This can be ascribed to the effect of lattice mismatch between Si and SnO₂, and also due to the effect of structural defects arising from porous structure that prevents high-crystalline SnO₂ film to grow.

The sensitivity, response and recovery characteristics of the sensor device have been studied by measuring the change in resistance, in the ambient and reducing gas atmosphere. The gas detection sensitivity (S) of the sensor device has been evaluated using the relation:

$$ S = (R_{a} - R_{g} )/R_{g} $$

(7)

where $R_{a} \,{\text{and }}\,R_{g}$ are resistance values of the sensor device in the ambient and reducing gas atmosphere, respectively. Variation of sensitivity as a function of response time is shown in Fig. 15. The maximum detection sensitivity of the sensor device toward H₂ and CO₂ gas is found to be 86 and 45 %, respectively. The figure depicts a short response time for H₂ and CO₂ gas, respectively, for reaching the maximum detection sensitivity indicated as above. The plot shows a non-exponential increase in sensitivity with response time and further indicates a saturation behavior in sensitivity for H₂ and CO₂ gas, respectively. The increase in sensitivity up to the saturation limit may be attributed to the raise in charge carrier density in the active surface, with the increase in time of gas exposure, due to rapid adsorption of gaseous species. This causes a fall in resistance, which consequently increases the sensitivity. On the other hand, saturation behavior of sensitivity, beyond the optimum response time (the time at which sensitivity reaches maximum), may be explained as follows: with the duration of exposure to gas, the gas interaction with the device active layer increases. After the culmination of optimum response time, the gas adsorption into the active layer reaches a saturation state causing the saturation of sensitivity.

Fig. 15

Variation of sensitivity with time a CO₂ and b H₂

Variation of detection sensitivity with the operating temperature is shown in Fig. 16. Sensitivity of the device increases with raise in operating temperature and reaches a maximum at 300 and 250 °C for H₂ and CO₂ gas, respectively. This may be attributed as follows: the rate of adsorption of the reducing gaseous species on to the active surface increases with the raise in operating temperature. This causes a rapid increase in the charge carriers and there by resulting in a decrease in resistance and an increase in sensitivity. Further, the figure shows a fall in sensitivity beyond the optimum operating temperature, which may be attributed as follows: beyond the optimum operating temperatures, the structural deterioration effects dominates, which causes desorption of gaseous species from the active surface and this mechanism becomes more rapid, as the temperature is increased, resulting in the fall in sensitivity (Sankara and Vivek 2007).

Fig. 16

Variation of sensitivity with operating temperature a CO₂ and b H₂

Conclusions

Transparent and conducting SnO₂ thin film has been produced on (quartz, ITO, silicon and porous silicon) substrates using rapid photothermal oxidation of pure Sn in air at 600 °C oxidation temperature and different oxidation time. The structural, optical, electrical properties, scan electron microscope and atomic force microscope of the prepared films were studied. The transmittance T in the visible and NIR was investigated; the allowed direct energy gap was determined to be 3.18 eV at optimum condition of 600 °C and 90 s. The dependence of the resistivity on the film thickness and oxidation time has been studied. The optimum thickness of high transmittance and lowest resistivity is about 150 nm for SnO₂ were ρ = 1.7 × 10⁻³ Ω cm and T = 88 %. The sensitivity behaviors of the n-SnO₂/p-PSi/c-Si-based gas sensor to H₂ and CO₂ gas were investigated.