Introduction

Surprisingly, the successful development of shale gas reservoirs, with the help of hydraulic fracturing technology, changes the overall energy landscape of the world, accounting for the 40% of natural gas production according to the 2016 reports, and it shares potential to further climb up to 45% in 2035 (Cao et al. 2019; Collell et al. 2015; Hughes 2013; Li et al. 2016a, 2016b). Thus, a clear understanding and comprehensive knowledge about the inherent fluid flow mechanisms inside shale reservoirs turns to be more and more urgent and crucial, which however is still a challenging issue and remains to be properly addressed (Sun et al. 2017, 2018a, 2018b; Tang et al. 2018a, 2018b; Whitby et al. 2008; Wu et al. 2019b). In accordance with the well-acknowledged research, shale rock can be classified as organic matter and inorganic matter, both of which possess inherent super heterogeneity feature and therefore are hard to be precisely characterized (Li et al. 2019; Xiong et al. 2019b). Moreover, the pore dimension in the above both matters fall into the typical nanoscale, ranging from several to thousands of nanometers, where the wall–molecule interactions will take the pronounced role affecting fluid flow performance (Feng et al. 2016; Huang et al. 2018a, 2018b). In contrast, the wall–molecule interactions can be overlooked in macroscopic scale; the classic NS equation, designed to capture fluid flow behavior in large scale, has not considered the interaction. Hence, the complexity induced by heterogeneity as well as ultra-small pore scale renders the flow behavior inside realistic shale matrix extremely difficult to be identified (Feng et al. 2020; Ji et al. 2021a, b; Li et al. 2021). Other than that, in light of the broad application scope, lots of research attention have been attracted on this heat research topic. In this paper, the emphasis is the methane flow performance through realistic shale matrix under different displacement pressures, mimicking the gas production from the shale reservoirs. Also, a theoretical framework for realistic shale matrix nanopores, constructed by kerogen molecules, is proposed and shares the obvious advantage for reproducing basic surface wettability, roughness in shale than previous work.

There exist many excellent methods to shed light on the methane flow capacity through shale matrix, which can be generally divided into four major categories, including laboratory experiments, analytical theoretical method, lattice Boltzmann method, as well as molecular dynamics simulations. As for the laboratory experimental method, membrane filled with nanoscale pores, similar to shale matrix featured with nanopores, is utilized to investigate the methane flow flux under various circumstances, including pressure, temperature, pore size distribution. Guo et al., (2015) investigated the nitrogen flow through membranes with diverse pore throat sizes (20, 55, and 100 nm) based on experimental apparatus, and an apparent permeability model is established based on experimental data. Wang et al., (2019) developed a novel experimental method to determine permeability of tight porous media. Although a great deal of experimental efforts has been conducted and related reliable results have been achieved, the experiments for porous media with nanopores are expensive and time-consuming to examine an equilibrium flux at a certain pressure difference (Wu et al. 2013; Majumder et al. 2005; Sun et al. 2019a, 2019b). The fatal deficiency of the experimental method is the limitation of atmosphere pressure, the shale gas reservoirs have fairly high pressure; however, current experimental devices are hard to achieve and remain it. Additionally, the data accuracy measured from experimental investigation heavily depends on apparatus up to date (Qiu et al. 2019; Ji et al. 2021a, b; Zhao et al. 2019; Zhao and Huang 2021) and is still unfavorable, especially for the nanoscale experiments. In contrast, on the basis of relative mature theory and reasonable assumptions, a lot of analytical models have been proposed to capture multiple gas flow mechanisms or fluid storage modes inside both shale organic/inorganic matrix, encompassing gas adsorption, surface diffusion, water distribution features, wall roughness (Sheikholeslami et al., 2020, 2021a, 2021b). Notably, each theoretical model has its own applicable criterions or suitable conditions and may fail to generate desirable results, particularly at nanoscale pores (Bao et al. 2017a, 2017b; Wang et al. 2017). As a result, the analytical models, coupling classic theories and multiple key flow mechanisms, inevitably suffer limitations for practical application toward realistic cases. Recently, lattice Boltzmann method is widely applied to describe the fluid flow capacity through nanopores by modifying the slip boundary of N-S equation (Chen et al. 2015; Zhang et al. 2018a, 2018b, 2018c). However, it is important to highlight that lattice Boltzmann equation is proposed to solve fluid flow issues at mesoscale; therefore, the applicability will be dramatically weakened for nanoconfined fluid flow. Although newly discovered physical equations or phenomenon can be incorporated into the lattice Boltzmann equation, it is still challenging to ensure the reliability and accuracy of the results predicted from this approach. In terms of the aforementioned brief review, it demonstrates that laboratory experiments, analytical models, and lattice Boltzmann equations are difficult to simulate the nanoconfined fluid flow performance. Especially for shale gas reservoirs, featured with nanopores with different surface wettability and complex attributes, applicability of the above methods breaks down (Zafar et al., 2021; Zuo et al. 2020). Thus, it is significantly urgent to seek another sensible pathway to address this issue.

Stemming from the fundamental Newton’s second law and well-developed empirical force field parameters for various atoms, molecular simulation is almost regarded as the most reliable technical tool to investigate fluid interactions and flow behavior at molecular scale and nanoscale (Ho et al., 2019; Kazemi and Takbiri-Borujeni 2016; Tesson and Firoozabadi 2018; Ungerer et al. 2014; Wang et al. 2016; Wu and Firoozabadi, 2019a; Xiong et al. 2019a, Zeng et al. 2018; Sun 2019b). Under the solid theoretical background, molecular simulation data share high credibility; also the reliability of molecular simulations has been verified frequently compared with experimental results across abundant application industries. Molecular dynamics simulation is able to capture molecular interactions at atom scale, which is the key aspect affecting nanoconfined gas flow behavior, and the other methods fail to characterize this point. Currently, the majority of molecular simulation investigations about shale matrix focused on the fluid adsorption characteristics inside kerogen (organic matter) or inorganic matter. In addition, some scholars use the graphene-based nanopore to study the fluid flow feature through shale organic matter, rather than kerogen molecules. The graphene-based nanopore is constructed by smooth carbon nanotube, the surface wettability, chemistry, and roughness considerably differed compared to realistic shale matrix nanopore. It can be attributed to the complexity for constructing a sensible shale matrix with composition of amorphous kerogen molecules. As a result, with the intent of elaborating methane flow behavior through realistic shale organic matrix, the knowledge gap toward the construction of matrix nanopore should be filled at first. A simple while practical method is proposed here, a series of NVT and NPT ensembles for desirable atmosphere conditions, to construct nanopore by compressing kerogen molecules, the nanopore maturity can be adjusted by altering kerogen type. Then, methane flow simulation is performed by utilization of non-equilibrium molecular dynamics (NEMD), methane density and velocity distribution under different displacement pressure presented. Furthermore, nanopore geometry, pore radius, displacement pressure are considered seriously in this simulation study.

The paper content is arranged following the way below. The nanopore construction method with the use of kerogen molecules is introduced at first, laying the physically basis for this work. Then, based on the kerogen nanopore and NEMD, gas flow behavior, mainly the density and velocity distribution feature, through shale organic nanopore is revealed. After that, limitations of this research and prospect in terms of the domain are discussed from our best knowledge. Finally, several key insights are drawn.

Construction of nanopores inside kerogen matrix

Nanopore construction work is necessary and performed before the molecular simulation at nanoscale. As for the organic matter, little research efforts have devoted to kerogen nanopores; the nanopore surrounded by kerogen molecules, sharing the natural similarity compared to shale rock. With the help of large-scale atomic/molecular massively parallel simulator (LAMMPS), 30 kerogen molecules can be compacted, and the realistic shale matrix can be obtained under several NPT (isothermal–isobaric with a constant molecular number) ensembles. Notably, the molecular structure of Kerogen I-A, able to reach an excellent match with that of experimental data for realistic kerogen molecules, is collected from Ungerer er al (2014). Detailed structure of a single kerogen molecule is provided in Fig. 1 on the left. Total 30 kerogen molecules are inserted into a relatively large simulation box to generate an initial low-density value, as it is shown in Fig. 1 on the right. Multiple tests demonstrate that the initial low density is beneficial for low-energy system, as well as quick stable state (Sun et al. 2020). Simulation box is set as a cubic box with side length of 200 Å, which is larger than that in existed documents and appears to have a positive impact on obtainment of the stable configuration. The initial system density is about 0.03 g/cm3.

Fig. 1
figure 1

The molecular structure of Kerogen I-A (left) and initial configuration of organic matrix (right)

Full size image

Also, boundary condition at the all three directions of the simulation box is set as periodic boundary. Notably, both the methane molecules and kerogen molecules are assigned with CVFF force field by using Molecular Studio software. The force field has been frequently utilized to characterize the molecular behavior of kerogen, which shows pretty good feasibility. The deviation may take place and enlarge if an inappropriate force field is selected; other force field parameters can be utilized to enhance the calculation accuracy. Other than that, the cutoff distance for short-range interactions inside the simulation box is assigned as 9.5 Å. And the long-range interactions are calculated with the utilization of particle–particle/particle-mesh method.

After several cycles of NVT as well as NPT ensembles, the system will approach stable state with the desirable atmosphere temperature and pressure; the duration lasts 12 h in this paper and fluctuates based on the computational power. With the high-pressure value set in NPT ensemble, the entire simulation box will shrink, and overall density will gradually increase. The temperature at the final step of construction process is set as 400 K, a typical shale gas reservoir temperature with depth of 2000 m, and the corresponding pressure will be stable at 200 Bar. The side width of the final simulation box is about 66 Å, and the skeletal density of kerogen is close to 1.06 g/cm3. The skeletal density is a critical indicator to examine the reliability of the constructed nanopore, supposed to be close to realistic shale matrix. Wu et al., (2019a, b) have compacted 60 type-II kerogen molecules, and the final density is 1.03 g/cm3. And the kerogen matrix established by Collell et al., (2015) achieves an average density of 0.96 g/cm3. Thus, the density generated from this research work is close to that from previous scholars, which means that the configuration of kerogen matrix is relatively reasonable. As depicted in Fig. 2 on the left, the matrix has been presented, and a circular nanopore with radius of 1 nm at the center of matrix is shown. Notably, the nanopore inside kerogen matrix is obtained by inserting some dummy atoms at the initial configuration and remaining positions of these atoms unchanged during the above ensembles. Finally, removing dummy atoms leads to the vacant circular space, forming the kerogen nanopore eventually. After that, placing specified numbers of methane molecules during NVT ensemble will lead to a certain atmosphere pressure when the simulation becomes stable, which can also be called as the equilibrium molecular dynamics (EMD). Kerogen molecules will be set as fixed after kerogen nanopore is obtained; only the position or velocity of methane molecules will change based on the specific NVT or NPT ensemble. The molecular configuration at the final step of EMD is provided in Fig. 2 on the right.

Fig. 2
figure 2

Sketch of physical model of circular nanopores inside kerogen matrix

Full size image

Gas flow simulations

After the above EMD simulation, the organic nanopore, kerogen nanopore in this paper, in shale is constructed. Then, NEMD starts by adding a body force at a specific direction on the methane molecules inside the circular nanopore space. Notably, attracted by the surrounding kerogen molecules, several methane molecules may enter into kerogen matrix during EMD simulation. And these methane molecules will hardly return to the circular nanopore and will not be assigned with the additional force during NEMD simulation. In this work, two sets of force are set, including 0.0005 kcal/mol/Å and 0.001 kcal/mol/Å, which is referred as small and large force, respectively, in the following technical context. The NEMD is mimicked at a constant temperature controlled by a thermostat. Special attention should be arisen that velocity in the flow direction is excluded for the computation of system temperature. Moreover, during NEMD simulation process, the kerogen matrix is remained as stationary, meaning the kerogen matrix is set as a rigid body with zero velocity. All the methane molecules are free to move, adsorption/desorption within the entire system. Generally speaking, NEMD will take longer time to reach an equilibrium than that of the EMD simulation, because the stream velocity is not easy to form with the interference of thermal velocity, especially when the small additional force is imposed. Based on the statistics, the equilibrium time for large force in this paper is about 5 ns and that for small force is about 7 ns. Anyway, both the two cases with different forces are simulated with 10 ns, ensuring the whole system reaches the equilibrium and the results can make sense. More importantly, associated flow behavior data of the final 2 ns are collected for further analysis. In addition, methane velocity and density contours are extracted, which are shown in the following part.

Results and discussion

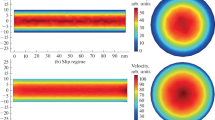
First of all, methane flow behavior under large displacement force is presented; the corresponding velocity and density contour from NEMD are depicted in Fig. 3. Observing the technical content in velocity contour in Fig. 3 on the left, it can be demonstrated that high velocity value will tend to take place at the center of the nanopore, and the methane velocity at the vicinity of kerogen surface will close to zero. Basically, the methane adsorption will happen near the kerogen surface, its thickness approaches several methane molecular diameters, and the adsorption methane is believed to lose mobility. One feature should be highlighted that the system pressure at this paper is about 65 MPa, the high-pressure atmosphere for shale gas reservoirs. And the pore radius of the circular nanopore is about 1 nm. As for the velocity contour, it can be further demonstrated that the actual flow region is smaller than the pore cross section, which means that methane velocity is zero with a distance away from the pore surface, about 5 Å in this research, instead of the nanopore boundary. Analyzing the velocity contour in Fig. 3, it can be further concluded that the methane flow in nanopores has the similarity with that of continuum flow to some extents, which seems to obey the parabolic principle. The phenomenon may be the results from the high pressure, which will lead to low Knudsen number, defined as a ratio of molecular mean free path to nanopore size, for methane flow in nanopores. The fluid flow will be dominated by continuum flow when Knudsen number falls into the range lower than 0.001. In the meanwhile, from the density contour shown in Fig. 3 on the right, it can be found that position where density peak occurs is near the pore surface, which can be considered as the adsorption phenomenon induced by interactions between nanopore surface molecules and methane. Combining the two figures in Fig. 3, an interesting conclusion can be drawn that the velocity of adsorption gas, i.e., density peak, is nearly zero, failing to contribute to the overall confined methane flow capacity. Thus, under relatively high pressure, the velocity distribution in nanopores will be like parabolic. In addition, adsorption methane molecules fail to flow like that in the center of the nanopore. However, surface diffusion mechanism, a special interface phenomenon that adsorption molecules may hop and move at the direction of displacement pressure, has been reported. It provides the possibility that adsorption methane can contribute to flow behavior based on surface diffusion; however, this research has not captured this point. More importantly, it can be easily found from Fig. 3 that strong heterogeneous characteristics regarding methane density takes place, different from homogeneous feature generated from the graphene-like material. From analysis, the heterogeneous features are originated from the heterogeneous nature of kerogens, which is exactly the characteristics of realistic shale matrix, i.e., the well-acknowledged fact that highly heterogeneity exists. And the research content in this paper can present the characteristics directly, sharing the advantage over other existed literatures to be more suitable tool to evaluate the fluid flow behavior through actual shale matrix.

Fig. 3
figure 3

Velocity and density contour generated from NEMD with large additional force

Full size image

When the additional force assigned on the methane molecules becomes small, i.e., small displacement pressure, it is attractive to present the velocity and density contour again. Comparing the output results from large force with that from small force, the effect of pressure difference on nanoconfined methane flow will be clarified. As we all know, at the macroscale where the classic Darcy equation still holds, the velocity profile has a linear positive relationship with pressure difference. Thus, a critical question raised up and required to be properly answered that the relationship will still hold or not. As illustrated in Fig. 4 on the left, the velocity contour feature is overall flat, indicating that pressure difference indeed has a direct positive impact on methane flow velocity. However, it should point out that the linear relationship will break down. Because only the methane molecules inside the nanopore are free to move, the velocity of atoms surrounding the methane in Fig. 4 is zero and stays stationary as the matrix system. From the observations, methane molecules fail to move efficiently under the small displacement pressure; velocity of the entire molecules is close to zero. This phenomenon may be correlated to the minimum displacement pressure, a critical value that fluid flow behavior starts once pressure difference exceeds it, or remains still. The minimum displacement pressure should be mainly affected by pore size, climbing with decline of pore size. As for the nanopores, where surface–molecule interactions are crucial, the surface chemistry, wettability, and roughness may also affect the minimum displacement pressure. The phenomenon requires extensive investigations in the future.

Fig. 4
figure 4

Velocity and density contour generated from NEMD with small additional force

Full size image

Collecting the methane velocity data of a cross section of the nanopore, the velocity distribution under different displacement pressure can be depicted in Fig. 5. With the large driven force, the velocity profile tends to have a parabolic feature with the fitting coefficient of 0.7489, while the velocity profile under the small driven force fails to capture the parabolic feature, indicating a relatively low fitting coefficient of 0.0387. At the same time, consistent with the above analysis, it can be demonstrated that displacement pressure always acts as a positive factor affecting the overall velocity value. Notably, the positive factor is different from that in classic Darcy equation. Also, it should be noted that the location of 100 Å is the center of the circular nanopore. And the pore radius is about 1 nm, i.e., 10 Å. The occurrence of velocity of methane outside of the nanopores can be observed in Fig. 5. This phenomenon can be attributed to the attraction of kerogen molecules toward methane during the NEMD simulation process. Finally, for Fig. 6, representing the density distribution in the nanopore with different driven forces. It can be observed that the two lines nearly coincide with each other, manifesting the density distribution will not be affected by pressure difference. The deviation between the both two lines is calculated and depicted in Fig. 6 as the pink line; the deviation is always close to zero. It suggests that pressure difference has little influence on the density distribution of methane molecules inside the nanopore. It further reflects that the dominant role played by surface–molecule interactions on fluid molecular distribution features.

Fig. 5
figure 5

Methane velocity distribution under various pressure differences

Full size image
Fig. 6
figure 6

Methane density distribution under various pressure differences

Full size image

Limitations and prospects

The investigation of nanoconfined gas flow behavior in shale matrix is meaningful, especially with nanopores constructed by kerogen molecules, rather than regular carbon-based material. This research provides a general technical framework to shed light on fluid behavior, including phase behavior, original distribution, and flow performance, in realistic shale matrix or coal matrix. However, several limitations should be highlighted here and researchers with interests should pay uttermost attention. At first, although the kerogen nanopore shares the evident advantage over carbon-based nanopore, the concrete difference between kerogen nanopore and realistic organic pore is still unclear and requires quantification. Actually, a certain amount of asphalt exists in shale organic matter, while the paper content fails to cover this point. After that, the pore geometry in the paper is considered as circle; actually many kinds of geometry are discovered for organic pores, like triangle, ellipse. Notably, kerogen nanopore with various pore geometry can be achieved by the proposed method by altering the geometry of the inserted dummy atoms in Section Construction of nanopores inside Kerogen matrix. Finally, shale matrix is composed by a lot of kerogen nanopores; the flow behavior through single nanopore is hard to represent that in shale matrix. Basically, changing the way inserting dummy atoms at the initial simulation system, shale matrix with complex spatially distribution can be obtained. As the research provides a pathway to construct porous media more similar to shale organic matter, the upcoming research can use the kerogen-based nanopore or nanoporous media to investigate interesting nanoconfined fluid behavior.

Summary and conclusions

  • A circular nanopore with radius of 1 nm surrounding with 30 type I kerogen molecules is constructed in this paper. Then the methane flow simulation is conducted with the utilization of NEMD nested in LAMMPS. Compared with the graphene-like material, the nanopore surrounded with several kerogen molecules is similar to the realistic shale organic pores regarding surface chemistry, which can provide more accurate evaluation about nanoconfined methane flow performance;

  • Skeleton density of the obtained shale matrix is nearly 1.06 g/cm3 at a normal atmosphere condition, clarifying its reliability by agreements with previous contributions. Two sets of force are added on the methane molecules inside the circular nanopore, i.e., 0.0005 kcal/mol/Å referred as small force and 0.001 kcal/mol/Å referred as large force. NEMD will take longer time to reach an equilibrium state than that of the EMD simulation, because the stream velocity is not easy to form with the interference of thermal velocity;

  • Under large driven force, the velocity distribution appears to obey the parabolic law, which can be attributed to low Knudsen number at the high atmosphere pressure, close to 65 MPa. It suggests that pressure difference acts as a dominant role affecting methane flow velocity; methane mobility is almost lost under small displacement pressure. Also, pressure difference fails to influence the density distribution, which is considered to be mainly controlled by the molecular–surface interactions.