Prediction performance advantages of deep machine learning algorithms for two-phase flow rates through wellhead chokes

Abstract

Two-phase flow rate estimation of liquid and gas flow through wellhead chokes is essential for determining and monitoring production performance from oil and gas reservoirs at specific well locations. Liquid flow rate (Q_L) tends to be nonlinearly related to these influencing variables, making empirical correlations unreliable for predictions applied to different reservoir conditions and favoring machine learning (ML) algorithms for that purpose. Recent advances in deep learning (DL) algorithms make them useful for predicting wellhead choke flow rates for large field datasets and suitable for wider application once trained. DL has not previously been applied to predict Q_L from a large oil field. In this study, 7245 multi-well data records from Sorush oil field are used to compare the Q_L prediction performance of traditional empirical, ML and DL algorithms based on four influencing variables: choke size (D₆₄), wellhead pressure (P_wh), oil specific gravity (γ_o) and gas–liquid ratio (GLR). The prevailing flow regime for the wells evaluated is critical flow. The DL algorithm substantially outperforms the other algorithms considered in terms of Q_L prediction accuracy. The DL algorithm predicts Q_L for the testing subset with a root-mean-squared error (RMSE) of 196 STB/day and coefficient of determination (R²) of 0.9969 for Sorush dataset. The Q_L prediction accuracy of the models evaluated for this dataset can be arranged in the descending order: DL > DT > RF > ANN > SVR > Pilehvari > Baxendell > Ros > Glbert > Achong. Analysis reveals that input variable GLR has the greatest, whereas input variable D₆₄ has the least relative influence on dependent variable Q_L.

Introduction

One of the key factors in determining the production performance of oil/gas reservoirs is to establish value of the variables influencing two-phase flow rate in oil and gas wells (Lak et al. 2014; Choubineh et al. 2017; Ghorbani et al. 2017b, c, 2019; Mirzaei-Paiaman and Salavati 2013). To determine the flow rate of each well (gas with condensate/oil), to control and stabilize the flow, and to prevent reservoir damage by creating a back pressure on the reservoir, a well reducer is typically installed (Ghorbani et al. 2019). Well reducers help to protect well equipment as well as the reservoir. The back pressure created by them helps to control pressure and flow rate (Mirzaei-Paiaman and Salavati 2013; Guo 2007; Al-Attar 2009; Chong et al. 2009; Nasriani et al. 2016; Mirzaei-Paiaman and Salavati 2012; Omana et al. 1969; Poettmann and Beck 1963). The increase in well-bore pressure associated with well reducers is due to the presence of oil-soluble gas or gas condensate, which forms in the wellbore due to pressure drop in the production tubing.

Wellhead reducers belong to two categories (Bairamzadeh and Ghanaatpisheh 2015; Gorjaei et al. 2015): (A) fixed chokes or positive chokes (Fig. 1) and (B) variable chokes (Fig. 2). In fixed chokes the bore or aperture diameter cannot be changed. In variable chokes the bore or aperture can be increased or decreased to adjust fluid flow rate through it (Gorjaei et al. 2015; Elhaj et al. 2015).

Fig. 1

Image of fixed or positive wellhead chokes with 32/64 in or ½ in apertures

Fig. 2

Schematic diagram showing internal components of a variable wellhead choke (Ghorbani et al. 2017c; Latif et al. 2012)

In fields with many wells, it is often not practical to measure flow rates directly at each well head choke. Rather, it is necessary to estimate flow at individual wells from available measurements of influencing variables. In this study, we evaluate and compare the liquid flow rate (Q_L) prediction performance of four machine learning (ML) algorithms: support vector regression (SVR), decision tree (DT), random forest (RF) and artificial neural network (ANN) with a deep learning neural network (DL) based on four key influencing variables. The four influencing variables considered are choke size (D₆₄), wellhead pressure (P_wh), oil-specific gravity (γ_o) and gas–liquid ratio (GLR) are evaluated. The superior performance of the DL demonstrates that it is better suited than the ML algorithms to provide reliable and accurate Q_L predictions with large datasets. A dataset of 7245 data records (made available to readers) from ten wells in the offshore Sorush oil field (Iran) forms the basis of the analysis presented.

Theory of two-phase fluid flow through wellhead chokes

The principles of two-phase fluid flow are as follows:

• (A) When a fluid flows through a flow pipeline, the fluid pressure is initially above the bubble point, i.e., the gas remains dissolved in the liquid.

• (B) When the fluid is at the bubble point, gas bubbles begin to emerge from the liquid and it becomes a two-phase fluid.

• (C) When the fluid pressure drops below the bubble point pressure, the fluid moves in a pipeline as two-phase flow.

Key reasons for involving wellhead chokes in a production flow stream are: (1) to create a pressure drop in the flow stream to prevent damage to well equipment, (2) to facilitate separation of gas from oil in separators; and (3) to create a back pressure on the reservoir to assist in maintaining reservoir pressure.

Although biphasic flowmeters were developed decades ago, their high-cost and ongoing calibration requirements to accurately calculate of two-phase fluid flow have limited their uptake. Calculating the exact GLR value inside the well reducer itself, while a well is online, is costly and requires the installation of accurate measurement sensors. In practice, estimated GLR data are typically used to calculate fluid flow rates through wellhead chokes.

Flow regimes in two-phase flow through wellhead chokes

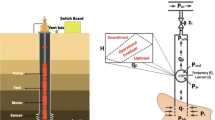
For two-phase fluids (liquid and gas) passing through a choke, critical and subcritical flow regimes may occur (AlAjmi et al. 2015; Zarenezhad and Aminian 2011). Critical flow (sonic) occurs when the fluid flow reaches the speed of sound. In this type of flow, the fluid’s flow rate has no effect on the downstream pressure and occurs in a state of downstream-pressure independence (Perkins 1993; Al-Attar 2008a, b). It is more difficult to estimate the fluid flow rates under subcritical flow regimes, where the ratio of outlet pressure to pre-reducing pressure (inlet pressure) is greater than 0.588 (Bairamzadeh and Ghanaatpisheh. 2015; Gould 1976; Safar Beiranvand et al. 2012; Nasriani and Kalantari ASL 2011). The ratio of the output pressure (P_downstream), inlet pressure (P_upstream), determined by Eq. (3) can distinguish between critical and sub-critical flow regimes, as displayed in Fig. 3 (Guo 2007; Al-Attar 2008a, b; Gould 1976; Safar Beiranvand et al. 2012; Nasriani and Kalantari ASL 2011; Guo and Ghalambor 2012; Ling 2012):

$$ \frac{{P_{downstream} }}{{P_{upstream} }} = \left( {\frac{2}{k + 1}} \right)^{{\frac{k}{k - 1}}} $$

(1)

where P_downstream = choke outlet pressure downstream of the choke; P_upstream = pressure upstream of the choke; and, k = C_p/C_v and is referred to as the ratio of specific heat.

Fig. 3

Choke performance in terms of flow rate versus downstream to upstream pressure ratio (Kaydani et al. 2014)

One of the tasks that has been done in recent years is to use field data to calculate and predict, as well as to determine the parameters used in the oil and gas industry, for example in the following areas have been addressed: reservoirs (Ghorbani et al. 2017a); formation damage (Mohamadian and Ghorbani 2015), wellbore stability (Darvishpour et al. 2019), rheology and filtration (Mohamadian et al. 2018), production (Ghorbani and Moghadasi 2014a; Ghorbani et al. 2014b; 2017b); drilling fluid (Mohamadian et al. 2019).

Tangeren et al. (1949) conducted fundamental studies on fluid flow through constraints, focusing on bubble point pressure and critical flow conditions. They achieved these conditions by adding gas bubbles to incompressible fluids to prevent upstream and downward pressure transfer associated with a restriction. Gilbert (1954), based on 260 data records for chokes ranging in size from 6/64 inches to 18/64 inches, developed empirical Eq. (2) for critical flow (Table 1). Various modifications to the Gilbert equation have been proposed, including those of (Baxendell 1958), Ros (1960), Achong (1961), and Pilehvari (1981) (Table 1) Eq. (3–6). These modifications are based on observations of data from different regions and a wide range of chokes size. They achieve variable prediction accuracy for two-phase flow rates through the wellhead chokes.

Table 1 Empirical equations proposed for fluid flow across oil field chokes

Safar Beiranvand et al. (2012) evaluated 748 production flow data records from 10 oil wells in Iran, with choke sizes ranging from 16/64 to 40/64, based on which they proposed Eq. (7) for flow rate prediction (Table 1). In that relationship, the percentage of water production, measured as base solids and water (BS&W), is added to the Gilbert Equation (1954). Ghorbani et al. (2019) based on 82 wellhead choke data measurements spanning liquid flow rates from < 100 to 30,000 stock tank barrels/day (STB/D) proposed flow rate prediction Eq. (8) (Table 1), which also included BS&W in its formulation. Mirzaei-Paiaman and Salavati (2013), based on 102 production flow data records, proposed Eq. (9) (Table 1), in which oil density and gas-specific gravity are added to the Gilbert equation.

Choubineh et al. (2017), considering information from 235 production flow-test data records, proposed Eq. (10) (Table 1). The advantage of Eq. (10), compared to the other formulations described, is that it takes fluid temperature into account.

Machine learning (ML) algorithms

Developments over recent years of industrial automation and intelligent machine monitoring and recording technologies, mean that large digital datasets are now routinely available for system behavior pattern analysis. Machine learning (ML) systems are flexible intelligent computer algorithms that provide data-driven tools for improving automated learning and prediction capabilities for many systems ML algorithms achieve cognition and learning through data-record variable relationships and pattern recognition to build an intelligent model for making predictions and decisions (Bonaccorso 2017).

In recent years, several researchers have applied ML methods to flow measurement through wellhead or production-unit choke in oil and gas fields. Table 2 compiles some such recently published ML studies and the flow rate prediction accuracies they have achieved.

Table 2 Some applications of machine learning methods to predict two-phase flow through wellhead choke

Development from shallow to deep learning models

The structure of simple neural networks (SN), including artificial neural networks (ANN), is inspired by the neural communications and cognitive structures observed in animal and human brains (Barrow 1996). Such networks consist of a large number of interconnected neural processing units (neurons or nodes), each of which, when configured in a sequential processing system, creates a specific communication pattern in response to a specific input or stimulus (Pouyanfar et al. 2018). Environmental perception sensors derived from raw input information activate neurons in the input layer of SN network. Subsequently, other neurons located in the next layer, hidden inside the network, are activated based on the weighted communications they receive from the input-layer neurons (Schmidhuber 2015). Improvements in computer capacities and speeds now make it possible to rapidly process information passed through neural networks involving more neurons and/or more hidden (Pouyanfar et al. 2018). Deep ANN or DNN architectures represent an improved version of traditional ANN (Rolnick et al. 2017) which mainly consist of an input layer, one hidden layer, and an output layer. On the other hand, DNN consist of a feed-forward neural network with a large number of neurons, most of which are distributed across multiple hidden layers (Saikia et al. 2020). Deep learning methodologies exploit new training methods and communication algorithms among the neurons, helping them to develop high prediction performance and reliability from multi-layered learning models.

Machine learning (ML) versus deep learning (DL)

Big data analysis

In technical terms, DL is a powerful subset of ML methods that has been developed in a similar way to meet challenges and limitation of many classical machine-learning techniques when confronted with processing large data sets (“big data”) characterized by having many data records and many input variables, and/or unstructured data fields such as involved in image and speech recognition algorithms (Nguyen et al. 2019). DL techniques tend to offer improved efficiency and accuracy as the size of the data set increases (Zhang et al. 2018). For smaller datasets, classical ML algorithms often outperform DL networks, certainly in terms of execution speed. On the other hand, DL networks often require little or no supervision (additional training) once they are initially trained/calibrated, whereas ML models typically require more supervision and re-training as part of their development and application.

Feature extraction

Classical ML algorithms usually cannot be implemented directly on a raw data records incorporating many variables (high dimensionality). Such algorithms require a raw-data, pre-processing step, typically incorporating feature extraction/selection (Zheng and Casari 2018). The performance of classical ML techniques is highly dependent on the user-based presentation quality of the input data. Inconsistent quality of the data presentation and/or the allocation of inappropriate parametric weights often leads to poor results and generally can compromise ML performance (Pouyanfar et al. 2018). Effective ML feature selection depends upon a human user possessing sufficient knowledge and understanding of a system and the potential data inconsistency problems it incorporates. In contrast, DL algorithms automatically perform feature selection without the need for human user intervention. Hence, DL models with higher processing capacity and enhanced feature recognition capabilities are often able to provide accurate prediction models either without or with much less human assistance/input (Goodfellow et al. 2016).

Economic and interpretation perspectives

Implementation of DL algorithms on multi-dimensional and complex “big data” systems requires the use of powerful computational processors. These can be costly as they need to be capable of conducting and storing the large numbers of calculations and/or intermediate data manipulations required in a reasonable timeframe. On the other hand, ML algorithms can typically be executed using standard, low-cost PC-grade computer systems. Since the feature selection process in most classical ML models is not performed automatically, users typically gain a better understanding of the various factors associated with the input variables that influence the ML algorithms prediction performance, which can be helpful when tuning the control parameters associated with an ML model’s configuration. On the other hand, users tend to be blind to the internal functions used by DL models in the automated feature selection, making them behave, in many cases, like “black boxes”.

Figure 4 shows the generic differences in the network architecture and implementation usually associated with ML and DL algorithms.

Fig. 4

Generic differences in the network architecture and execution of ML and DL algorithms

There are only a limited number of studies available that have focused the unique capabilities of DL algorithms on topics related to fluid flow measurement. Loh et al. (Loh et al. 2018) trained and then tested the long short-term memory (LSTM) deep learning model to predict real-time production rate using two gas-well datasets that were experiencing salt-deposition issues. Ezzatabadipour et al. 2017 implemented a multilayer perceptron (MLP) algorithm with three hidden layers, configured as a deep learning model, to predict patterns of multiphase flow, based on 5676 data records of gas and liquid two-phase flow in inclined pipes. Wen et al. (Wen et al. 2019) introduced a modified recurrent (RU-Net) algorithm which is a deep convolutional neural network (CNN) extending the U-Net architecture, originally developed for biomedical image segmentation, to successfully predict multiphase flow in porous media involving CO₂ injection. They used 128 feature maps composed of 2-D plans extracted from radially plotted coordinates of a wellbore subjected to CO₂-injection the inputs for their model included series of permeability, injection duration, injection rate, and saturation fields planes.

Many research articles have applied ML methods to two-phase flow rate prediction through wellhead chokes. However, to the authors’ knowledge no results have so far been published applying DL models to make such predictions. In this study, a comparison of the flow rate prediction performance of DL and ML models is provided using a substantial dataset (7245 data records from three wells). It reveals that DL models can outperform ML models for the dataset evaluated.

Methodology

Workflow diagram

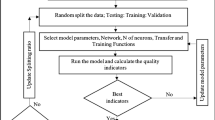
A workflow diagram (Fig. 5) summarizes the steps involved in constructing, evaluating and comparing prediction performance of DL and ML algorithms in two-phase flow rate prediction through wellhead chokes. The process sequence begins with data collecting followed by data variable characterization, including the determination of the maximum and minimum values ​​for each data variable involved. This information is used to normalize all data variables to range between + 1 and -1 by applying Eq. (11).

$$ x_{i}^{l} = \left( {\frac{{x_{i}^{l} - xmin^{l} }}{{xmax^{l} - xmin^{l} }}} \right)*2 - 1 $$

(11)

where $x_{i}^{l} = {\text{ the}}\;{\text{value}}\;{\text{of}}\;{\text{attribute}}\;{\text{for}}\;{\text{data}}\;{\text{record}}\;I;$,$xmin^{l} = {\text{ the}}\;{\text{minimum}}\;{\text{value}}\;{\text{of}}\;{\text{the}}\;{\text{attribute}}\;{\text{among}}\;{\text{all}}\;{\text{the}}\;{\text{data}}\;{\text{records}}\;{\text{in}}\;{\text{the}}\;{\text{dataset}};\;{\text{and}},$$xmax^{l} = {\text{ the}}\;{\text{maximum}}\;{\text{value}}\;{\text{of}}\;{\text{the}}\;{\text{attribute}}\;{\text{among}}\;{\text{all}}\;{\text{the}}\;{\text{data}}\;{\text{records}}\;{\text{in}}\;{\text{the}}\;{\text{dataset}}.$

Fig. 5

Schematic diagram of the workflow sequence applied for comparing the prediction performance of ML and DL algorithms

The normalized data records are then allocated to training and testing subsets. In this study, 80% of the data records comprising a dataset are allocated to the training subset and the remaining 20% of the data records are allocated to the testing subset. The testing subset is held independently and in no way involved in the algorithm’s training procedure; it is used solely to test the flow-rate prediction performances of the trained algorithms. The relative prediction performances of the trained algorithms applied to the testing subsets are then used to identify the algorithm that provides the best prediction performance for the dataset.

Learning network algorithms evaluated

Learning networks combining various algorithms are now routinely applied to solve a wide range of petroleum engineering challenges, including: reservoirs (Ghorbani et al. 2020a), production (Choubineh et al. 2017; Ghorbani et al. 2017c; 2018; 2019; 2020a; 2020b), process (Ghorbani et al. 2018) and drilling (Mohamadian et al. 2021; Rashidi et al. 2020) drilling trajectories (Atashnezhad et al. 2014); and fluid processing (Wood 2018). In this study, we evaluate and compare the following ML and DL algorithms.

Support vector regression (SVR)—ML model

Cortes and Vapnik (1995) developed the support vector machine (SVM) algorithm in 1991 on the basis of statistical learning theory. SVM has been used to solve a wide range of classification, regression and time series prediction problems (Cortez and Vapnik 1995; Cao and Tay 2003; Drucker et al. 1997; Kuo et al. 2013; Shao et al. 2020; Smola and Schölkopf 2004; Rui et al. 2019; Vapnik 2013; Ahmad et al. 2020). For classification SVM applies kernel functions to map input nonlinear vectors into higher dimensions and a hyperplane is constructed within the feature space separating data into two classes. SVM strives to maximize boundary separation between the classes and the hyperplane for the training subset by establishing the support vectors. A regression-based SVR model (Brereton et al. 2010; Pan et al. 2009) is constructed here to predict two-phase flow rate through wellhead chokes.

SVR models require dataset to define their input variables $[{x}_{i}]\in X={R}^{n}$ and their corresponding output (or dependent) variable ${y}_{i}\in X=R$ where $i=\mathrm{1,2},3,\dots , N$. N is the total number of data records present in the dataset. The dependent variable of each data record, ${y}_{i}$, is the prediction target. That prediction is achieved by accurately fitting a regression function $y=f(x)$. The target values are approximated by SVR using a learning function expressed as Eq. (12).

$$ f\left( {x,\omega } \right) = \omega \phi \left( x \right) + b $$

(12)

where $f\left( x \right) = \;{\text{SVR}}\;{\text{target}}\;{\text{prediction}};$ $\omega \in R^{n} = \;{\text{the}}\;{\text{weight}}\;{\text{vector}};$ $b \in R = {\text{ the}}\;{\text{threshold}}\;\left( {{\text{bias}}} \right);\;{\text{and}},$ $\phi \left( x \right)$ = the high-dimensional feature space mapping from low-dimensional space x. Coefficients $\omega$ and $b$ are derived by minimizing of the regularized risk function (Eq. 13).

$$ \frac{1}{2}\omega^{2} + C\frac{1}{l}\mathop \sum \limits_{i = 1}^{n} L_{\varepsilon } \left( {y_{i} ,f\left( {x_{i} ,\omega } \right)} \right) $$

(13)

where ${\Vert \omega \Vert }^{2}$ = smoothness or flatness of the function; C = a regularization factor which is the measure of the trade-off extent between the model flatness and empirical error; and $\frac{1}{l}\sum_{i=1}^{1}{L}_{\varepsilon }({y}_{i},f\left({x}_{i}\right))$= an empirical error that is measured using an $\varepsilon$-insensitive loss function expressed by Eq. (14).

$$ L_{\varepsilon } \left( {Y_{i} ,f\left( {x_{i} ,\omega } \right)} \right) = \left\{ {\begin{array}{*{20}c} {0,y_{i} - f\left( {x_{i} ,\omega } \right) \le \varepsilon } \\ {y_{i} - f\left( {x_{i} ,\omega } \right) - \varepsilon ,\,{\text{otherwise}}} \\ \end{array} } \right. $$

(14)

where the range of $\varepsilon$ values is defined (Eq. 10) such that the loss is equal to zero when the value predicted falls within the range, while the loss is equal to the difference between $\varepsilon$ of the range and predicted value when that predicted value does not fall within the range.

The ω and b coefficients can be estimated using transformation of the regularized risk function (Eq. 9) into the original objective function (Eq. 15) by introducing two positive constants, $\xi and {\xi }^{*}$, also known as slack variables.

$$ \begin{aligned} Min \frac{1}{2}\omega^{2} + C\frac{1}{l}\mathop \sum \limits_{i = 1}^{l} \left( {{ }\xi_{i} - \xi_{i}^{*} } \right) \hfill \\ Subjected to \left\{ {\begin{array}{*{20}c} { y_{i} - f\left( {x_{i} ,\omega } \right) - b \le \varepsilon + \xi_{i} } \\ {f\left( {x_{i} ,\omega } \right) + b - y_{i} \le \varepsilon + \xi_{i}^{*} } \\ {\xi_{i} ,\xi_{i}^{*} > 0} \\ \end{array} } \right. \hfill \\ \end{aligned} $$

(15)

This convex optimization expression (Eq. 11) can be solved by applying a Lagrangian multiplier strategy (Shao et al. 2020; Smola and Schölkopf 2004; Rui et al. 2019; Vapnik 2013; Ahmad et al. 2020). Equation (16) defines the transformed equation with these multipliers.

$$ f\left( {x,\alpha_{i} ,\alpha_{i}^{*} } \right)\mathop \sum \limits_{i = 1}^{N} \left( {{ }\alpha_{i} - \alpha_{i}^{*} } \right)\left( {\phi \left( {x_{i} } \right).\phi \left( x \right)} \right) + b $$

(16)

in which the ${\alpha }_{i}$ and ${\alpha }_{i}^{*}$ represent the Lagrangian multipliers. The input vectors ${x}_{i}$ that correspond to ${\alpha }_{i}-{\alpha }_{i}^{*}=0$ are called support vectors established using the variable information associated with the training subset’s data records. An appropriate kernel function also needs to be defined in order to overcome the computation complexity involving high-dimensional space (Rui et al. 2019). Any function that satisfies Mercer’s condition might be employed as a kernel function (Vapnik 2013). The four kernel functions commonly used with SVR (Smola and Schölkopf 2004; Vapnik 2013) are listed in Table 3.

Table 3 Kernel functions commonly used with SVM and SVR algorithms

Among all the kernel functions applied, the radial basis function (RBF) kernel, known also as the Gaussian kernel, is the most common kernel applied with SVM and possesses an ability of anti-interference to noise in data (Kuo et al. 2013; Liu and Xu 2014; Wu et al. 2018; Vapnik et al. 1996; Hashemitaheri et al. 2020). In this study, the RBF kernel is used with the SVR algorithm to predict two-phase flow rate (${Q}_{l}$) through a wellhead choke. The control parameter values applied to that SVR model are listed in Table 4.

Table 4 SVR wellhead choke flow model control parameter values

Decision tree

Decision trees are a popular machine-learning method widely applied to evaluate diverse datasets, both classification and regression (Nie et al. 2011; Tsai and Chiou. 2009; Lorena et al. 2007). Groups of data records are organized into a hierarchical structure consisting of nodes and ramifications governed by a set of rules. This makes them applicable to classification and numerical (regression) datasets, although they are more widely used for classification problems (Lorena et al. 2007; Osei-Bryson 2004; Ortuño et al. 2015). For solving classification problems, a class label is given to each leaf of the tree with the data classes discriminated by rules and allocated to specific leaves. Three steps are involved in constructing decision trees for machine learning applications:

• (a) Distinguishing variables between input (or attribute) variables and dependent (or target) variables.

• (b) Dividing the data records at “child” nodes, based on defined rules, using a splitting algorithm that assesses the attribute variables.

• (c) Conducting further splitting, whereby each child node acts as parent node from which further nodes and decision-tree layers are generated.

A simple decision tree is illustrated in Fig. 6 distinguishing the different types of nodes involved. From the root node (top layer) the entire dataset of data records is initially split into two subsets, which become the child (or decision) nodes forming the second layer of the tree. The child nodes are then divided further into sub-nodes, forming additional layers of child nodes, and ultimately reaching a final layer with terminal nodes (or leaves). A splitting algorithm is applied to ensure homogeneity (consistency) of the data records allocated to each child node. The data splits applied at each node are established by the algorithm to achieve the highest degree of homogeneity at each sub-node. Clear distinguished (homogeneous) groups of data records are established in the layer with the terminal nodes.

Fig. 6

Typical structure of a decision-tree machine-learning model

The tree is developed (layers added) until the training subset data records are perfectly classified by the tree so that they are allocated to the correct leaf with 100% accuracy. However, when the trained decision tree is applied to another dataset (e.g., an independent testing subset) it is typically unable to classify those data records perfectly, indicating overfitting by the initial training process. The more layers and nodes involved in a decision tree the greater the risk of overfitting (Czajkowski and Kretowski 2016; Liu et al. 2016; Fakhari and Moghadam 2013).

In this study, a the scikit learn (sklearn) decision tree module (Scikit-Learn 2020a, b) is coded in Python applying the “gini” criterion to establish feature importance and the “best” splitter is applied to decide which feature and the value of the threshold to apply in making each split (Table 5). This is used to predict the two-phase flow rate (${Q}_{l}$) through a wellhead choke.

Table 5 Decision tree wellhead choke flow regression model control parameter values

Random forest

The random forest algorithm represents an extension to the decision tree algorithm, as it constructs and develops multiple decision trees to evaluate. It is a supervised, predictive algorithm suitable for the classification and regression applications based on training and testing subsets of data records for which the input and dependent variables distinguished (Zhou et al. 2020; Grape et al. 2020). The multiple decision trees are constructed in parallel, each using relatively few layers/nodes. This approach reduces the likelihood of overfitting, compared to algorithms based on individual decision trees. It also decreases the variance and bias of the prediction results, without compromising decision accuracy, by assessing the predictions of all decision trees collectively (Ahmad 2018; Breiman 2001).

To train random forest ML models, subsets of data records are bootstrapped (i.e., randomly samples with replacement) from the full dataset. Each subset of bootstrapped data records can then be used to develop an unpruned classification or regression decision tree. Not all input variables (M) are used in the development of each tree as candidates for splitting; rather, a small, randomly selected number of the available input variables (G) are selected randomly for each tree and then used for the splitting operation. Multiple decision trees are built iteratively until a specified number of trees (K) are available. In regression (numerical) problems, predictions of the dependent variable are made through aggregation of predictions (bagging) from all the individual regression trees developed. The bagging processing reduces complexity of the individual trees and tends to diminish the chances overall of the algorithm overfitting the training subset. The prediction function for the random forest algorithm is expressed as Eq. (17).

$$ \hat{f}_{RF}^{K} \left( x \right) = \frac{1}{K} \mathop \sum \limits_{k = 1}^{K} T_{i} \left( x \right) $$

(17)

where K = number of individual regression trees; X = input variable vector; and, ${T}_{i}(x)$ = prediction from a single regression tree for the i^th data record.

An out-of-bag error estimation (OOB) is progressively performed as the forest of individual regression trees is constructed. OOB is derived using the unselected data records (the OOB subset) as a test for the $k$ th tree once it is trained in the bagging process. The OOB subset provides a progressive unbiased estimation of generic prediction error prior verifying the prediction accuracy of the aggregated results using the independent testing subset. The relative importance of each input variable, in relation to the dependent variable predictions, can be assessed from the aggregated results. This is helpful in reducing dimensionality of the model by eliminating low-contribution input variables to enhance the model’s efficiency on datasets with high dimensionality (Ahmad et al. 2017). There are various ways to achieve this. One is to switch two input variables in the tree solutions, while keeping the remaining variables constant, and recording the mean reduction in the prediction accuracy. This makes it possible to rank the relative importance of each input variable to prediction accuracy achieved for the dependent variable (Ahmad 2018). The random forest algorithm is illustrated in Fig. 7.

Fig. 7

Schematic diagram of generic configuration of random forest algorithm

In this study, a regression random forest model, as described, was established using the Scikit Learn Random Forest Regressor (Scikit-Learn 2020a, b) to predict two-phase flow rate (${Q}_{l}$) through a wellhead choke. The control parameters for the random forest model are listed in Table 6.

Table 6 Random forest wellhead choke flow regression model control parameter values

Artificial neural network (ANN)

ANN is one of the most widely used ML algorithms for solving nonlinear problems across many fields of engineering (Shahbaz et al. 2019) despite their reputation of acting black boxes due to their hidden layers of regression-like calculations (Wood 2018). There are several types of ANN algorithms applied with feed-forward neural network (FFNN) composed of single-hidden-layer and multi-hidden-layer perceptron's (MLP) both being popular. In this study, a single-hidden-layer ANN (Fig. 8) is constructed for predicting two-phase flow rate (${Q}_{l})$ through a wellhead choke.

Fig. 8

Indicative structure of a feed-forward artificial neural network (ANN) with a single hidden layer with multiple neurons

The information passed from the neurons of one layer to the neurons of the next layer in the ANN is adjusted by weight and bias vectors. The neurons in the hidden layer perform information processing and send processed signals forward to the output layer adjusted by an activation function. Equation (18) expresses the signal adjustments made as information flows through the ANN

$$ y_{i} = f\left( {\mathop \sum \limits_{i = 1} W_{ij} x_{i} + b_{j} } \right) $$

(18)

where $f$ = the activation function; $b_{j}$ = the hidden layer bias;$x_{i} { }$ = input for the i^th variable i; and, $W_{ij}$ = connection weight between the i^th input and j^th neuron.

The neural network is trained, typically with a backpropagation algorithm, to improve its prediction performance, by adjusting the weights and bias values applied to the hidden layer. It does this by minimizing the mean squared error between actual and predicted values collectively for all data records the training subset, as defined by Eq. (19).

$$ E_{MSE} = \frac{1}{m}\sum\limits_{i}^{m} {\left( {\hat{y}_{i} - y_{i} } \right)}^{2} $$

(19)

where $\hat{y}_{i} { }$ = actual value of dependent variable for the i^th data record; $y_{i}$ = predicted value of dependent variable for the i^th data record; and m = the number of data records in the training subset.

The prediction performance and convergence speed/efficiency of ANN can often be improved by applying alternative optimization algorithms to backpropagation. Many optimizers have been applied for this purpose including Adam, RMSprop, Adagrad, Adadelta, Momentum, and Nesterov Accelerated Gradient. In this study, the RMSprop optimizer is applied, because it is an enhanced gradient-based algorithm that progressively divides the calculated gradient by a rolling average of recently attained gradient values (Selvam 2018). The initial learning rate of RMSprop is updated for different weights according to Eq. (20) and (21).

$$ E\left[ {g^{2} } \right]_{t} = 0.9E\left[ {g^{2} } \right]_{t - 1} + 0.1g_{t}^{2} $$

(20)

$$ \theta_{t + 1} = \theta_{t} - \frac{{\upeta }}{{\sqrt {E\left[ {g^{2} } \right]_{t} + \smallint } }}g_{t} $$

(21)

where $E\left[ {g^{2} } \right]_{t}$ = rolling average gradient at iteration t; $g_{t}$ = gradient of objective function at iteration t; $\theta_{t}$ = objective function value at iteration t; $\in$ = smoothing term (avoiding division by zero); and $\eta { }$ = learning rate, for which a default value of 0.001 is typically applied.

Equation (21) shows that the learning rate $\eta$ is divided by exponentially decaying rolling average of squared gradients (Kartal and Özveren 2020).

The network structure of the single-hidden-layer ANN model has on input layer that includes the same number of neurons as input variables, one output layer with 1 neuron for the dependent variable prediction, and one hidden layer with 500 neurons. The model is configured and executed in Keras (Keras 2020), a deep learning package coded in Python, running on top of the machine learning platform TensorFlow (TensorFlow 2020). The control parameter values of the constructed ANN model are listed in Table 7.

Table 7 Control parameters for the one-hidden layer ANN model constructed to predict two-phase flow rate (${{\varvec{Q}}}_{{\varvec{l}}})$ through wellhead choke

Certain control parameters involved require some clarification:

min_delta This is used to define the algorithm’s stopping criteria. The minimum change in the objective function qualifies as an improvement. This depends on the scale of the dependent variable and will be dataset specific.

Patience: This is also used in relation to the algorithm’s stopping criteria number of iterations with no improvement after which training of the algorithm is terminated.

Activation function: The Scaled Exponential Linear Unit (SELU) function is applied as it facilitates self-normalization. By internalizing normalization, it tends to speed up convergence.

Learning rate: It controls the magnitude of change to apply to the model in each iteration based on magnitude of the prediction error. This value is used to adjust the values of the weights and biases.

Selection of suitable values for “min-delta” and “patience”, and identifying a high-performing activation function, requires some trial-and-error analysis with each dataset as the optimum selection depends on the character of the data records.

A flow diagram summarizing the sequence of steps through which the ANN progresses to make its dependent-variable predictions is displayed in Fig. 9.

Fig. 9

Flow diagram of single layer ANN built for prediction of QL through wellhead chock

Deep neural network (DNN)

Deep neural network (DNN) or deep learning (DL) algorithms represent a further development of ANN, containing multiple hidden layers each typically configured with a large number of neurons. A typical structure of DL algorithm containing three hidden layers is illustrated in Fig. 10. As with ANN, the hidden layers contain a specified number of neurons, with weights, biases, and activation functions applied. In the DL algorithm, each layer’s output is communicated as input for the next layer by applying Eq. (22) beginning with the input layer of the network where network is $h^{0} = x$ (Lee et al. 2018).

$$ h^{k} = \left( {W^{k} h^{k - 1} + b^{k} } \right)\sigma^{k} $$

(22)

where $k$ = number of DNN network layers; ${h}^{k}$ = the array of output for the $k$ layer; ${W}^{k}$ = neuron weights for the $k$ layer; ${b}^{k}$= bias for the $k$ layer; and, ${\sigma }^{k}$ = activation function for the $k$ layer.

Fig. 10

Indicative structure of a deep learning neural network (DNN) with three hidden layers with multiple neurons

The final layer’s output, $\widehat{y}$, is the dependent variable’s prediction. The purpose of using the activation functions is to emphasize the nonlinearity of relationships between the input and output variables (Taqi et al. 2018). Key characteristics of activation factors are that they should be differentiable making them easier to apply particularly with gradient-based optimizers (Bengio 2009; Asghari et al. 2020; Nwankpa et al. 2018). The activation functions that are widely used with DNN are listed in Table 8.

Table 8 The most common activation functions

In DL algorithms, the dissimilarity (error) between the predictions and the actual values of dependent variables is minimized by conducting training with a training dataset of substantial size. An objective function that represents this dissimilarity is defined to train DL algorithms. The objective functions commonly used to train DL algorithms on a dataset with n samples are listed in Table 9.

Table 9 Common objective functions minimized during the training process of deep learning (DL) models

From the outset of the training process, the values of the weights applied to neurons and biases applied to each layer of the DL network are initialized to each have values of 1. The DL model begins by making predictions based on random changes to the initial weights. Then, using an optimization algorithm, the weight and bias values are iteratively updated in order to minimize the objective function.

The typical control parameters applied to configure DL models include the number of layers, number of neurons within each layer, objective function used for training, activation function applied to each layer, optimization algorithm, minimum delta, patience (i.e., early stopping criteria), learning rate, and split percentages between training and testing subsets. Most of these control parameters need to be established by trial and error to suit specific data sets (Ng 2016). The control parameters selected for the developed DL model are listed in Table 10.

Table 10 Control parameters for the multi-layer DL model constructed to predict two-phase flow rate (Q_L) through wellhead choke

The sequence of steps through which the DL progresses to make its dependent-variable predictions is the same as that described for the ANN model (Fig. 9).

Sorush oil field 10-well dataset evaluated

Data collection

The prediction of two-phase flow rate through wellhead chokes is conducted using a dataset of 7245 data records from 10 production wells drilled in the Sorush oil field (well numbers SR#17 to SR#26) and valorization by 113 datapoint of 12 well from South of Iran collected in Choubineh et al. 2017 article. This oil field is located in the Persian Gulf offshore southwest Iran in Bushehr province, 83 km southwest of Kharg Island (Fig. 11). Sorush oil field was discovered in 1962 with its discovery well achieving maximum daily production of 14,000 barrels. The Sorush oil field extends over an area of about 260 square kilometers and with more than 15 billion barrels of oil in place.

Fig. 11

Map showing the location of the Sorush oil field, offshore southwest Iran

The wellhead data measurements from the ten Sorush oil field wells and other data provided by Choubineh et al. 2017 include: choke size (D₆₄) is measured in 1/64 in, wellhead pressure (P_wh) measured in pounds per square inch gauge (psig), oil specific gravity (γ_o) relative to water, gas to liquid ratio (GLR) measured in Scf/STB and two-phase flow rate (Q_L) measured in stock-tank barrels per day. The first four represent input variables, and the last represent the dependent variable for the ML and DL models (Table 11). Values for the input and dependent variables for all data records are made available in an Excel supplementary file (Appendix 1).

Table 11 Data record statistical characterization of the variables in this study

Variable data analysis

Cumulative distribution functions (CDF) for the five dataset variables are displayed in Fig. 12 providing insight to the form of distributions displayed by these variables across all 7245 data records in Sorush Oil field. The percentage of the CFD values less than a specific variable value is calculated according to Eq. (23).

$$ F_{X} \left( x \right) = P\left( {X \le x} \right),for\;all\;x\; \in \;R $$

(23)

Fig. 12

The cumulative distribution function (CDF) of the Sorush field dataset variables for the prediction of two-phase flow rate through wellhead choke. The variables are choke size (D₆₄), wellhead pressure (P_wh), oil-specific gravity (γo), gas–liquid ratio (GLR), and two-phase flow rate through wellhead choke (Q_L; dependent variable). The thinner blue line represents the cumulative distribution functions for the data variables. The thicker red line represents a normal distribution with the same mean and standard deviation across all 7245 data records in Sorush Oil field

where P = percentage of data records with values in a distribution less than a specific data record; x = data variable value range; X = the value of variable x in a specific data record; and R = the dataset of data records.

Inspection of the CFDs (Fig. 12) reveals the following: for

• D₆₄ For ~ 13% of the data records D(1/64in) are < 48.64 in. For ~ 76% of the data records 48.64 < D₆₄ < 84.22 in. For ~ 11% of the data records D(1/64in) > 84.22 in. The D₆₄ data approximately follows a normal distribution with a slightly negative skew.

• P_wh For ~ 29% of the data records P_wh < 218.59 Psig. For ~ 62% of the data records 218.59 < P_wh < 553.03 Psig. For ~ 11% of the data records P_wh > 553.03 Psig. The P_wh data deviate somewhat from a normal distribution and are more negatively skewed than the choke diameter distribution and display a proportionally higher standard deviation.

• γ_o For ~ 45% of the data records γ_o < 0.9293. For ~ 38% of the data records 0.9293 < γ_o < 1.05795. For ~ 17% of the data records γ_o > 1.05795. The γ_o data do not follow a normal distribution but are approximately symmetrical and display a relatively low standard deviation in relation to its mean value.

• GLR For ~ 39% of the data records GLR < 118 Scf/STB. For ~ 38% of the data records 118 < GLR < 150 Scf/STB. For ~ 24% of the data records GLR > 150 Scf/STB. The GLR data follow a normal distribution quite closely displaying a moderate standard deviation.

• Q_L For ~ 49% of the data records Q_L < 11,623 STB/D. For ~ 42% of the data records 11,623 < Q_L < 16,710 STB/D. For ~ 9% of the data records Q_L > 16,710 STB/D. The Q_L data approximately follow a normal distribution and are essentially symmetrical with a moderate standard deviation.

Of the input variables, γ_o and P_wh are the most asymmetrical and distributed least like normal distributions. The characteristics of the variable distributions are shown in more detail in Fig. 13, with the relative shapes of the distributions highlighting that these variables are nonlinearly related.

Fig. 13

Variable value versus dataset index number highlighting the ranges and extreme values associated with each variable recorded for the Sorush oil field dataset. The variables displayed are: choke size (D₆₄), wellhead pressure (P_wh), oil-specific gravity (γo), gas to liquid ratio (GLR), and two-phase flow rate through wellhead choke (Q_L) across all 7245 data records in Sorush Oil field

Measurements to determine prediction errors

The entire dataset of 7245 data records in Sorush oil field is divided for each case run into a training subset (80%) and a training subset (20%). Statistical analysis of the prediction errors for the two-phase flow rate through choke (Q_L) associated with each of the ML and DL algorithms is conducted using the following widely used metrics: percentage deviation (PD), average percentage deviation (APD), average absolute percentage deviation (AAPD), standard deviation (STD), mean squared error (MSE), root-mean-squared error (RMSE), and coefficient of determination (R²). The computation formulas for these statistical measures are expressed in Eq. (24–31).

Percentage difference (PD):

$$ {\text{PD}}_{{\text{i}}} = \frac{{{\upxi }_{{\left( {{\text{Measured}}} \right)}} - {\upxi }_{{\left( {{\text{Predicted}}} \right)}} }}{{{\upxi }_{{\left( {{\text{Measured}}} \right)}} }}x 100 $$

(24)

Average percent deviation (APD):

$$ APD = \frac{{\mathop \sum \nolimits_{i = 1}^{n} PD_{{\text{i}}} }}{{\text{n}}} $$

(25)

Absolute average percent deviation (AAPD):

$$ AAPD = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {PD_{{\text{i}}} } \right|}}{{\text{n}}} $$

(26)

Standard deviation (SD):

$$ SD = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {PD_{{\text{i}}} - Dimean} \right)^{2} }}{{{\text{n}} - 1}}} $$

(27)

$$ Dimean = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\xi_{Measured\;i} - \xi_{\Pr edicted\;i} } \right)} $$

(28)

Mean square error (MSE)

$$ MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{Measured\;i} - \xi_{\Pr edicted\;i} } \right)^{2} $$

(29)

Root-mean-square error (RMSE):

$$ RMSE = \sqrt {{\text{MSE}}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - y_{i} } \right)^{2} }}{n}} $$

(30)

where n = number of data records; $x_{i}$ = measured dependent variable value for the i^th data record; and $y_{i}$ = predicted dependent variable value for the i^th data record.

Coefficient of determination (R²):

$$ R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\xi_{\Pr edicted\;i} - \xi_{Measured\;i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\varphi_{\Pr edicted\;i} - \frac{{\mathop \sum \nolimits_{I = 1}^{n} \xi_{Measured\;i} }}{n}} \right)^{2} }} $$

(31)

Results

Two-phase flow rate prediction accuracies achieved by ML, DL, and traditional mathematical models

In order to make comparisons between ML, DL, and traditional empirical methods for two-phase flow rate (Q_L) prediction, and to determine the best performance accuracy achieved for all 7245 data records in Sorush oil field, the following method is applied:

Two-phase flow rate (Q_L) prediction accuracies achieved by the training subset (~ 80%), the testing subset (~ 20%), and the complete dataset (5796 data records) are presented in Tables 12, 14, respectively. Analysis of these results reveals that the relative performance accuracy of ML, DL, and traditional empirical methods can be ranked in the following descending order: DL > ML > traditional empirical methods, respectively. The deep learning model achieves the highest Q_L prediction accuracy for the three sample sets evaluated: RMSE < 195.90 STB/D and R² = 0.9969 for the testing subset; RMSE < 161.23 STB/D and R² = 0.9981 for the training subset; and, RMSE < 144.21 STB/D and R² = 0.9978 for the total dataset.

Table 12 Q_L Prediction performance compared for ML, DL, and traditional mathematical (empirical) models applied to the training subset (5796 data records from Sorush oil field) for the Sorush field dataset of wellhead choke recordings

Among the empirical models considered, the Pilehvari model achieved the best relative Q_L performance accuracy: RMSE < 1522.6 STB/D and R² = 0.7012 for the testing subset; RMSE < 1507.1 STB/D and R² = 0.7331 for the training subset; and, RMSE < 1510.1 STB/D and R² = 0.7178 for the total dataset.

Analysis of results

Figure 14 and Tables 12, 13, 14 display RMSE and R² comparisons of performance accuracy of ML, DL, and traditional mathematical models. Analysis of these results confirms that the Q_L prediction accuracy of the DL model substantially outperforms the other models considered. The poorer Q_L prediction accuracy of the empirical models identifies that they can be ranked in descending order of accuracy, as follows: Pilehvari > Baxendell > Ros > Glbert > Achong.

Fig. 14

Two-phase flow rate (Q_L) prediction accuracy expressed in terms of R² and RMSE and compared for the full dataset (7245 data records) of Sorush oil field data records for all the prediction methods evaluated

Table 13 Q_L Prediction performance compared for ML, DL, and traditional mathematical models applied to the independent testing subset (1449 data records from Sorush oil field) for the Sorush field dataset of wellhead choke recordings

Table 14 Q_L Prediction performance compared for ML, DL, and traditional mathematical models applied to the entire dataset (7245 data records from Sorush oil field) for the Sorush field dataset of wellhead choke recordings

Close inspection of the model’s prediction results (Tables 12, 13, 14) reveals that the deep learning model achieves exceptionally high Q_L predict ion accuracy (RMSE = 195.9 STB/D; AAPD = 1.025% for the testing subset) and is substantially more accurate than the four ML models applied to the Sorush field dataset. The near-perfect R² value is achieved due to the large number of closely spaced samples in the dataset. Figure 15 displays the predicted versus measured Q_L values for each data record in each subset evaluated by the five models. The Q_L prediction performance of the five proposed models enables them to be ranked in the following order: DL > DT > RF > ANN > SVR.

Fig. 15

Two-phase flow rate (Q_L) prediction versus measured valued for each data record in the training and testing subsets and the full dataset evaluated for the Sorush oil field wellhead measurements related to all 7245 data records from Sorush oil field

The Q_L prediction results for each model applied to the full dataset (7245 data records) can be compared more closely by superimposing their results on a single predicted versus measured Q_L graph (Fig. 16). This reveals that the predictions from the ML models demonstrate significant scatter in comparison with the ML model that closely follows the X = 1 line with much less dispersion in Fig. 15. In detail, the ML models show a tendency to overestimate at the lower end of the Q_L range (< ~ 7500 STB/D) and underestimate at the upper end of the Q_L scale (> 20,000 STB/D). That tendency is particularly apparent for the RF and ANN models and partly explains their lower accuracy performance overall.

Fig. 16

Two-phase flow rate (Q_L) prediction versus measured valued for each data record in the full dataset evaluated for the Sorush oil field wellhead measurements related to 7245 data records from Sorush oil field

Figure 17 compares the prediction performance of the models on a sample-by-sample basis for all data records in terms of relative prediction error (PD%; Eq. 20) for both the training and testing subsets for the Sorush oil field. Whereas the DL model shows consistently low relative percentage errors across the sample index range, the ML models show some high PD values at various points throughout the sample index range. The higher prediction errors are on the negative side (i.e., underestimation of Q_L). The ANN model shows more PD errors more negative than -2% than the other models (Fig. 16). On the other hand, the SVR, DT and RF models show a PD% for one data record more negative than -5%. In terms of their Q_L values both subsets of data records are spread across the entire Q_L value range. They are displayed sequentially in Fig. 17 for illustrative purposes only. The range (-0.14762% >  =  < 0.142185%) of relative percentage errors achieved by the DL model is almost an order of magnitude less than the other four models, emphasizing the superiority of its Q_L predictions for the Sorush oil field dataset evaluated.

Fig. 17

Two-phase flow rate (Q_L) prediction relative percentage errors compared for the training and testing subsets of the five prediction models evaluated for all 7245 data records from Sorush oil field

The histograms included in Figs. 18 display the Q_L prediction errors for the ML and DL algorithms. The superiority of the DL model is clear in terms of the lower prediction errors it generates. The best performing ML model is DT which consistently outperforms the RF model. On the other hand, the SVR and ANN ML models consistently show poorer QL prediction performance than the other ML models when applied to this dataset.

Fig. 18

Error (STBD) histograms with fitted normal distributions (red line) for DL and ML models used to predict Q_L for all 7245 data records from Sorush oil field

Figure 19 distinguishes critical flow from subcritical flow regimes for the flow measured through the wellhead chokes of the wells in the Sorush oil field dataset. If the downstream pressure to upstream pressure ratio is <  = 0.588, the flow regime is identified as critical. On the other hand, if this ratio > 0.588, the flow regime is identified as subcritical. Analysis of Fig. 19 clearly reveals that this ratio is <  = 0.588 for almost all the data records evaluated for the Sorush oil field. Therefore, the flow through the reducers related to these 10 wells can be confirmed as conforming to a critical flow regime.

Fig. 19

Determination of the flow regimes in two-phase flow through wellhead chokes for the Sorush oil field dataset

Development and generalization of the deep learning model

The DL model developed in previous section has addressed solely the Sorush oil field (10 production wells) dataset. In order to evaluate the accuracy of the DL algorithms for general application to other oil fields, a published dataset of 113 data records from other fields (Choubineh et al. 2017) has been evaluated. This independent dataset includes data records from twelve oil wells located in South Iran. Statistical measures of Q_L prediction accuracy achieved for these data records are displayed in Table 15. A Comparison of the results of Table 15 with those displayed in Tables 12, 13, 14 confirms the high two-phase flow rate-prediction accuracy achieved by the developed DL model, trained with Sorush oil field data, when applied to other wells from other oil field.

Table 15 Q_L prediction accuracy of the DL model, trained with Sorush oil field subset (5796 data records), applied to the complete datasets available for 12 oil wells from South Iran (113 data records) treating them an independent testing subset

Figure 20 displays the actual versus the Q_L values predicted by the DL model trained with Sorush oil field training subset (5796 data records), applied to the complete datasets available for 12 oil wells from in South Iran. The performance accuracy achieved by this model confirms its reliability for application across the for 12 oil wells from South Iran. The method used is clearly suitable for application to other fields. However, it would be prudent to initially test the Sorush-calibrated DL model with some direct Q_L measured data for the specific fields to which it is applied in order to establish whether some recalibrations are required.

Fig. 20

Cross-plot of predicted versus measured Q_L values compared for the DL model trained with Sorush oil field training subset (5796 data records) and applied to the 113 data records available for 12 oil wells from South Iran

Figure 21 reveals the prediction performance of the Sorush-trained DL model applied to the 113 independent data records available for 12 oil wells from South Iran. Those data records are displayed sequentially in Fig. 21 for illustrative purposes only. The range of relative percentage errors achieved for this independent dataset is (−0.08611% >  =  < 0.159105%).

Fig. 21

Relative error (%) Q_L prediction by Sorush-trained DL model applied to the 113 data records available for 12 oil wells from South Iran

Discussion

It is useful to determine the relative influence of the input variables on the dependent variable (Q_L) values. Calculating the nonparametric Spearman’s correlation coefficient (ρ) is a useful measure to establish this. ρ is expressed over the range −1 (perfect negative correlation) to 1 (perfect positive correlation), with a zero value indicating no correlation and implying relatively low or no impact (Gauthier 2001). ρ is calculated for ranked data using Eq. (32).

$$ \rho = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \overline{O}} \right)\left( {M_{i} - \overline{M}} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - O} \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {M_{i} - \overline{M}} \right)^{2} } }} $$

(32)

where O_i = the value of data record i for input variable O; $\stackrel{-}{O}$ = the average value of the input variable O; M_i = the value of data record i for input variable M; $\stackrel{-}{M}$ = the average of the input variable M; and n = the number of data points in the population.

Figure 22 displays the p values for the relationships between Q_L and the four input variables considered in this study. It is apparent that GLR has the greatest relative impact on Q_L, whereas D (1/64) has the least influence. On the other hand, falling between the two input variables mentioned, Pwh and γo have almost equal influence on Q_L, the former directly and the latter inversely.

Fig. 22

Relationships of the two-phase flow rate prediction through wellhead choke individually with its input calculation variables: upstream choke size (D₆₄), wellhead pressure (P_wh), oil-specific gravity (γ_o), and gas–liquid ratio (GLR)

Many ML and DL algorithms display a tendency to overfit their training subsets, particularly with datasets consisting of relatively small numbers of data records. The substantial number of data records (7245) involved in the Sorush oil field dataset and the allocation of 20% of them (1449) to the independent testing subset have helped to avoid overfitting in this study. A comparison of the Q_L prediction accuracy achieved by the training (Table 12) and testing (Table 13) subsets indicates that overfitting has not impacted the prediction performance of any of the algorithms and traditional mathematical (empirical) models evaluated. Indeed, for the SVR and ANN a slightly higher prediction accuracy is achieved for the testing subset than for the training subset in terms of RMSE and R². For the other algorithms the prediction accuracy achieved by the testing subset is only slightly worse than the training subset, and the dispersion and magnitude of errors recorded across both subsets for each algorithm are similar (Fig. 17). The results of Fig. 19 identify that a critical flow regime prevails through the Sorush field wellheads. Figures 20, 21, and Table 15 demonstrate that the DL mode developed for the Sorush oil field can be successfully applied to wells from other fields.

Although overfitting has not been a problem for the large Sorush oil field dataset, that is unlikely to be the case for smaller datasets for these algorithms, particularly those characterized by a large number of neurons, layers or nodes. All of the algorithms evaluated lack transparency in readily revealing the details of how each individual data record prediction is generated. Future progress with DL algorithms needs to focus on improving their transparency and developing more clarity in their trade-off between prediction accuracy, complexity and overfitting risks. Despite this lack of calculation transparency, this study highlights the high-prediction performance of the DL algorithm with respect to flow rates through wellhead chokes across a wide range of magnitudes and multiple wells in the Sorush oil field. These results suggest sufficient reliability associated with the DL predictions to justify its incorporation with automated flow measurement systems for individual wells in that field. With careful calibration and training and sufficient data records to avoid overfitting this method offers the potential to improve flow rate prediction through wellheads in other oil fields.

Conclusions

In total, 7245 data records compiled for ten production wells from the Sorush oil field wells (SR#17 to SR#26) offshore Iran demonstrate the comparative performance of four traditional machine learning (ML), traditional mathematical (empirical) models, and one deep learning (DL) algorithm in predicting flow rate through wellhead chokes. The DL technique is a new technique that has not previously been applied for two-phase flow rate (Q_L) prediction.

The input variables choke size (D₆₄), wellhead pressure (P_wh), oil-specific gravity (γ_o), and gas–liquid ratio (GLR) are assessed by the algorithms to derive predictions of two-phase flow rate through the wellhead chokes (Q_L). The Q_L value ranges from 660 to 23,700 stock tank barrels/day (STB/day) for this dataset and shows nonlinear relationships with its influencing variables. Spearman's correlation coefficients reveal that the input variables GLR and γ_o are inversely related to Q_L, whereas input variables P_wh and D₆₄ display positive correlations with Q_L. D₆₄ shows the lowest correlation coefficient with Q_L of the four input variables evaluated. Prevailing flow through the wellhead chokes of the Sorush oil field conforms to a critical flow regime.

In addition to the deep learning neural network (DL), the ML algorithms evaluated are support vector regression (SVR), decision tree (DT), random forest (RF), artificial neural network (ANN). The traditional mathematical (empirical) models evaluated are those proposed by Gilbert (1954), Baxendell (1958), Ros (1960), Achong (1961), and Pilehvari (1981). The models are all used for two-phase flow rate prediction through wellhead choke for the Sorush oil field dataset. The large set of data records and the allocation of a substantial number of those records to an independent testing subset (1449 records or 20% of the entire dataset) enable the DL and ML algorithms to avoid overfitting with respect to this dataset. Based on six statistical measures of prediction accuracy, the DL algorithm substantially outperforms the four ML algorithms and five traditional mathematical models in predicting Q_L for this dataset.

The DL algorithm predicts Q_L for the testing subset with a root-mean-squared error (RMSE) of 196 STB/day and coefficient of determination (R²) of 0.9969 (in Sorush oil field). On the other hand, the RMSE for the four ML algorithms is greater than 590 STB/day. In order to test the suitability of the DL model for general application to predict Q_L in other oil fields, 113 independent data records from 12 wells from fields from South Iran were evaluated with the Sorush-trained DL model. The RMSE and R² for DL applied to that independent well dataset are 175. STB/day and 0.9983, respectively. These results suggest that the DL algorithm is a suitable choice for automating flow rate estimates through wellhead chokes, although for smaller datasets in other fields careful testing and calibration with measured Q_L data are required to eliminate the risk of overfitting.

Appendix 1

A supplementary Excel file containing the variable values for each of the 7245 data records from the ten wells from the Sorush oil field evaluated in this study is made available for readers to download.