Introduction

Permeability is the flow capacity of a reservoir. Without accurate measurement of rock permeability, valid predictions of reservoir performance cannot be achieved. Well testing, core analysis, and well logging are the most common methods of reservoir rock permeability measurement. While well testing and core analysis measure the permeability directly, the response of well logging tools gives an estimation of the reservoir permeability. Since all of these are expensive, especially the well testing and the core analysis tests, researchers have attempted to find inexpensive and efficient alternative approaches to estimate rock permeability.

Mercury intrusion porosimetry (MIP) is a well-known technique to characterize porous media. It describes pore throat size distribution, porosity, mercury-air capillary pressure, grain density, permeability, and tortuosity of reservoir rocks. Since MIP test could be performed on inexpensive drill cuttings samples, several researchers have attempted to derive permeability from MIP results. In addition to being inexpensive, drill cuttings are available for the entire well column from the surface to the bottom. Additionally, an equation which relates a dynamic rock property, e.g., capillary pressure, and its static properties, i.e., absolute permeability and porosity, can be effectively used for rock typing purposes (Al-Jawad and Saleh 2019; Dakhelpour-Ghoveifel et al. 2019; Fu et al. 2018). The precision and comprehensiveness of rock typing techniques are essential since they are used to infer reservoir dynamic properties from the estimated (usually from kriging) static ones.

Equation (1) which is known as Washburn (1921) equation, presents the relationship between pore throat radius and capillary pressure:

$$ r = C\frac{2\sigma \cos \theta }{{P_{c} }} $$
(1)

where r, σ, θ, Pc, and C denote the pore/throat radius (µm), the air-mercury interfacial tension (dynes/cm), the air-mercury contact angle (degrees), the capillary pressure (psi), and the conversion constant (0.145), respectively. Washburn (1921) equation is used as the basic theory for mercury intrusion porosimetry. Using current instruments, mercury can be intruded in nanopores having diameters as low as 3 nm.

Purcell (1949) linked absolute permeability to the area under the curve of mercury saturation versus \( P_{c}^{ - 2} \) obtained from MIP. He assumed that fluid flow through pores network satisfies Poiseuille’s law.

Thomeer (1960) observed the logarithmic plot of capillary pressure versus bulk saturation data gives a curve that can be approximated with a hyperbolic function based on which, he developed a relationship for capillary pressure data. The proposal was, there is an empirical relationship between permeability and the hyperbolic function.

Swanson (1981) introduced the following relationships to estimate air and absolute permeabilities:

$$ K_{a} = 399\left( {\frac{{S_{b} }}{{P_{c} }}} \right)_{\text{apex}}^{1.691} $$
(2)
$$ K_{w} = 355\left( {\frac{{S_{b} }}{{P_{c} }}} \right)_{\text{apex}}^{2.005} $$
(3)

where \( \left( {\frac{{S_{b} }}{{P_{c} }}} \right)_{\text{apex}} \) (or Swanson parameter) is the value of \( \frac{{S_{b} }}{{P_{c} }} \) corresponding to the apex of the approximated hyperbola. Moreover, Ka, Kw, Sb, and Pc represent air permeability (mD), absolute permeability (mD), mercury saturation (percent of bulk volume), and mercury capillary pressure (psi), respectively. Swanson’s relation is simple and is expressed as a nomograph. It can easily estimate the permeability from capillary pressure data of small rock samples and drill cuttings.

Katz and Thompson (1987, 1986) presented Eq. (4) to estimate permeability from mercury intrusion porosimetry data:

$$ K = \frac{{\phi L_{\rm{max} }^{3} }}{{226L_{c} }}S\left( {L_{\rm{max} } } \right) $$
(4)

where K denotes permeability (µm2), Lc is the threshold value of characteristic length (µm), and S(Lmax) is mercury saturation at maximum hydraulic conductance. In Eq. (4), it is assumed that if the pore throats having a diameter of Lmax (µm) are filled with mercury, the hydraulic conductance becomes maximum. Katz and Thompson used 50 samples to regress their equation. The permeability range of their samples was very wide (from 0.005 to 5000 mD), and their porosity range was unspecified. However, data from 50 samples are not enough to derive a correlation covering such a wide range of rock properties. In addition, their equation requires 3 parameters Lc, Lmax, and S(Lmax) to be specified prior to permeability calculation. It makes the calculation more complicated.

Winland developed a method to calculate the average pore/throat size in his research on the Weyburn, Spindle, and Hidalgo fields. As reported by Kolodzie (1980), the equation to calculate pore/throat radius (r35) is as follows:

$$ \log r_{35} = 0.732 + 0.588\log K_{\text{air}} - 0.864\log \phi $$
(5)

where r35 stands for the radius of the smallest pores/throats, which are filled by mercury at 35% mercury saturation in an MIP test (µm). In addition, ϕ and Kair denote porosity (%), air permeability (mD), respectively. The permeability and porosity ranges of the dataset used by Winland to derive his equation have not been mentioned.

Pittman (1992) tried to improve Winland’s work by performing regression on permeability, porosity, and MIP data of 202 sandstone samples. He stated that the following equation presents the best correlation:

$$ \log K_{\text{air}} = - 1.221 + 1.512\log r_{25} + 1.415\log \phi $$
(6)

where ϕ, Kair, are porosity (%), air permeability (mD), and r25 is the radius of smallest pores/throats, which are filled by mercury at 25% mercury saturation in a MIP test (µm).

Rezaee et al. (2006) used the same set of data from 144 carbonate samples to develop an equation in order to estimate permeability. The porosity ranged from 0.5 to 33.5% (with an average of 11%), and the range of permeability was between 0.006 and 414 mD (with an average of 21 mD). The maximum injection pressure in Rezaee et al.’s research was 1500 psi.

Utilizing regression, Rezaee et al. showed the smallest pore/throat radius filled by mercury at 50% mercury saturation (r50 in µm) has the highest correlation with the porosity and the permeability. Equation (7) shows their correlation:

$$ \log K = - 1.160 + 1.780\log \phi + 0.930\log r_{50} $$
(7)

where ϕ represents porosity (%), and K denotes gas permeability (mD).

Based on our investigations, tight samples cannot be fully intruded by mercury if the injection pressure is kept below 1500 psi. More than 80 samples, which were tested by Rezaee et al. (2006) were tight ones having permeabilities lower than 1 mD. This can cast serious doubts on the precision of Eq. (7) since the number of samples that were fully intruded during MIP tests was much less than the reported 144. On the other hand, Rezaee et al. (2006) equation can be applied to carbonates only. There is a need to develop an equation that can be employed for both carbonate and sandstone rocks.

In a similar work, Gao and Hu (2013) introduced an empirical and simpler equation to predict the permeability:

$$ \log K = 2.225\log r_{50} + 0.214 $$
(8)

Which has been derived from MIP results of just 18 samples. In Eq. (8), K and r50 represent the same parameters as in Eq. (7).

The permeability of the samples used by Gao and Hu (2013) ranged from 10−6 to 103 mD. Such a wide interval may not be properly covered by only 18 samples. Therefore, the validity of their correlation is questionable.

Most of the available studies have been performed on either sandstones or carbonates, solely; And a study for developing a comprehensive equation for both sandstone and carbonate rock types is missing. In the current research, 187 carbonate and sandstone samples used to derive a new correlation between uncorrected gas permeability, porosity, and pore/throat diameters.

In addition, the experimentally measured gas permeability values estimated using our correlation were compared with the values estimated by the equations proposed by Winland (1980), Katz and Thompson (1987, 1986), Rezaee et al. (2006), and Gao and Hu (2013).

The theory of mercury intrusion porosimetry

Mercury penetration, as a non-wetting phase into the core/plug samples, is modeled by Washburn (1921) equation, described in Eq. (1).

Mercury volume intruding into the pore spaces is measured as a function of injection pressure. This pressure–volume data can be used to characterize the pore structure of a rock sample. Equation (1) assumes porous media behaves like a bundle of cylindrical tubes with different radiuses, while in porous media, the pore/throat shapes are irregular, and there are more parameters (e.g., aspect ratios and coordination number) which affect the capillary pressure-injected mercury volume relationship. However, Washburn (1921) is a simple and widely accepted model of an otherwise complicated system.

Mercury surface tension depends on its degree of purity; nevertheless, the generally accepted value of 485 dynes/cm was used. Moreover, a constant value of 130 degrees for rock-mercury contact angle was considered.

Materials and methods

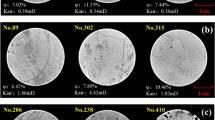
In order to construct a reliable correlation, it was tried to select enough number of samples with diverse properties to cover the entire property range. In the current research, 187 reservoir rock plugs with a wide range of permeability and porosity were tested (Figs. 1 and 2). The porosity of the samples was measured using a helium porosimeter. Additionally, samples permeability was determined by nitrogen flooding with a gas permeameter. The range of porosity of the samples was from 1 to 32% (with an average of 14.2%), and the range of their permeability was from 0.001 to 2000 mD (with an average of 68.7 mD). The lithology of the samples was identified to be sandstone, limestone, and dolomite (Fig. 3). The samples were selected from 8 different Iranian oil and gas fields. The samples which have surface vugs or showing pronounced double capillary pressure curves were not among our selection.

Fig. 1
figure 1

Permeability distribution of the samples

Full size image
Fig. 2
figure 2

Porosity distribution of the samples

Full size image
Fig. 3
figure 3

Lithology distribution of the samples

Full size image

Figure 4 shows the plot of the logarithm of the air permeability versus the porosity of the dataset used in this study. Because of the comprehensive range of lithology, porosity, and permeability of the samples, they were divided into seven hydraulic rock types. The samples in each rock type (group) have similar capillary pressures, and petrographic and flow properties. The capillary pressure curve for one sample (as the representative sample) from each rock type is plotted in Fig. 5 (The representative samples are highlighted in red in Fig. 4). Figure 5 shows the full range of the capillary pressure curves of the entire samples dataset.

Fig. 4
figure 4

The plot of the logarithm of sample air permeability versus sample porosity for different rock types

Full size image
Fig. 5
figure 5

Representative capillary pressure curves for each rock types

Full size image

In order to conduct MIP tests on the samples, a penetrometer containing a clean and dry cutting of the rock plugs was mounted into a low-pressure chamber of a Micromeritics Autopore IV 9500 apparatus. A schematic of the apparatus is depicted in Fig. 6.

Fig. 6
figure 6

Experimental setup of the mercury intrusion porosimetry test

Full size image

The penetrometer evacuation performed down to a pressure of less than 50 μmHg, and then mercury was allowed to fill the evacuated penetrometer at a pressure of 0.5 psia. Then, mercury as the non-wetting phase was intruded into the rock sample at stepwise-increasing pressures from 0.5 to 30.0 psia. At each step, equilibrium is assumed to be achieved when the injection rate dropped below 0.001 µL/g-s. Pressure and total intruded mercury volume at equilibrium were recorded in each step.

After equilibrium was established in the last pressure point (30 psia), injection pressure was dropped to atmospheric, and the penetrometer was removed from the low-pressure chamber and loaded into a high-pressure (up to 60,000 psia) chamber of Autopore system. Afterward, mercury injection continued at increasing incremental pressures until it reached 60,000 psia. The corresponding pore/throat radius of the final pressure was calculated to be 0.0015 µm from Eq. (1). The criterion for identifying equilibrium at each pressure point was the same as the low-pressure part.

In order to control the quality of the MIP test data, we weighed each dry samples prior to the test. After performing the MIP test, the sample was reweighed, and the intruded mercury volume was calculated using the weights difference and the density of mercury. The calculated volume of the intruded mercury was cross-checked by the injected volume reported by the MIP apparatus (Micromeritics Autopore IV 9500). Additionally, in order to ensure the full saturation of the sample, the intruded mercury volume has been cross-checked by the pore volume measured by the helium porosimeter.

The MIP tests were conducted in three distinct laboratories, MAPSA, Iran (126 samples), Corex, United Kingdom (33 samples), and PanTerra, Netherlands (28 samples).

Equation development

Using the curve fitting technique, we tried to find an equation correlating gas permeability, porosity, and pore/throat diameters of the samples, with the highest coefficient of determination. Values between r20 (smallest pore/throat radius, which was filled by mercury at 20% mercury saturation) and r60 (smallest pore/throat radius, which was filled by mercury at 60% mercury saturation) were examined. The results of the curve fitting are reported in Table 1.

Table 1 Results of regression analysis to establish a relationship between permeability, porosity and the smallest, mercury-filled pore/throat radiuses
Full size table

As it is shown in Table 1, the best coefficient of determination is obtained when r35 is used. Thus, the best equation to estimate permeability from porosity and pore/throat radiuses data is as follows:

$$ \log K = 0.0583 + 1.4660\log r_{35} + 0.6993\log \phi $$
(9)

where K is the gas permeability (mD), ϕ denotes porosity (%), and r35 is the smallest pore/throat radius that is filled by mercury at 35% mercury saturation (µm).

A cross-plot of measured and calculated permeabilities using Eq. (9) is shown in Fig. 7.

Fig. 7
figure 7

Cross-plot of measured and calculated permeabilities using Eq. (9)

Full size image

Permeability estimation comparison and validation

Carbonate rocks In order to evaluate the estimation precision of the proposed model, and to compare it with the other available models, the measured gas permeabilities of another 21 samples (including 13 limestones and 8 dolomites from two other Iranian oil and gas fields) were compared to the predictions of the proposed, Rezaee et al., Gao and Hu, Winland, and Katz and Thompson models. Figures 8 and 9 show a cross-plot of the measured and the calculated permeabilities for the new samples.

Fig. 8
figure 8

Cross-plot of the measured and the calculated permeabilities for the proposed, Rezaee et al., and Gao and Hu equations (carbonate samples)

Full size image
Fig. 9
figure 9

Cross-plot of the measured and the calculated permeabilities for the proposed, Winland, and Katz and Thompson equations (carbonate samples)

Full size image

As shown in Fig. 8, all the permeability values predicted by the proposed equation are closely scattered along the y = x line. Therefore, the proposed equation is able to make valid predictions for a wide range of permeability values of carbonate rocks.

Rezaee et al. equation has also predicted the permeabilities almost in good agreement with the measured data. Clearly, because Rezaee et al. equation was developed for carbonates specifically, it delivers good predictions for their permeability. However, Fig. 8 shows the predictions of Rezaee et al. relation suffers from higher errors than our correlation, especially for the lower and the higher ends of the permeability range.

The Gao and Hu equation highly underestimates the carbonate rocks permeability, and it seems, it would not result in valid predictions for carbonate samples.

Figure 9 depicts that the proposed equation predicts carbonates permeability better than two other equations, which are very popular in the petroleum industry. Even though both Winland and Katz and Thompson equations estimated permeability nearly in good agreement with the measured data, they underestimated it at medium and low ranges of permeabilities.

Figures 8 and 9 show that the proposed equation has the best performance among the tested correlations. Winland and Katz and Thompson equations make the next best predictions, respectively.

Table 2 represents the absolute average relative error (AARE) and the standard deviation (SD) of the relative error of the predicted permeabilities by each method for carbonate samples. AARE and SD values are defined as:

Table 2 The absolute average relative error (AARE) and the standard deviation (SD) of the relative error of the predicted permeabilities by each correlation for carbonate samples
Full size table
$$ {\text{AARE = }}\frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{X_{e} (i) - X_{c} (i)}}{{X_{e} (i)}}} \right|} $$
(10)
$$ {\text{SD = }}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\left| {\frac{{X_{e} (i) - X_{c} (i)}}{{X_{e} (i)}}} \right| - {\text{AARE}}} \right)^{2} } } $$
(11)

In which Xe(i) and Xc(i) represent logarithms of experimental and calculated permeabilities, respectively. Additionally, N denotes the number of data.

Sandstone rocks To check the precision of the predictions of the available correlations, 9 new sandstone samples from two other Iranian oil and gas fields were tested. Figures 10 and 11 show the cross-plot of measured and calculated sandstone permeabilities for the proposed, Rezaee et al., Gao and Hu, Winland, and Katz and Thompson equations.

Fig. 10
figure 10

Cross-plot of the measured and the calculated permeabilities for the proposed, Rezaee et al., and Gao and Hu equations (sandstone samples)

Full size image
Fig. 11
figure 11

Cross-plot of measured and calculated permeabilities for proposed, Winland, and Katz and Thompson equations (sandstone samples)

Full size image

As shown in Fig. 10, the estimations of the proposed model for the sandstones permeability are in good match with the experimentally measured data. Rezaee et al. equation underestimated permeability, especially for high permeability samples. Gao and Hu equation also underestimated permeability, especially for low permeability samples. The presented results in Fig. 10 show that Rezaee et al. equation gives more accurate results than Gao and Hu correlation for sandstone samples, although it has been derived for carbonate rocks.

Figure 11 shows that the proposed equation predicted sandstone permeability better than Winland and Katz and Thompson equations. Both Winland and Katz and Thompson equations suffer from underestimation at all ranges of permeability.

Among Winland, Katz and Thompson, Gao and Hu, and Rezaee et al. equations, the Gao and Hu equation has the lowest precision. Three other equations yielded reliable performance for estimating sandstones permeability.

Table 3 represents the absolute average relative error (AARE) and the standard deviation (SD) of the relative error of the predicted permeabilities by each method for sandstone samples.

Table 3 The absolute average relative error (AARE) and the standard deviation (SD) of the relative error of the predicted permeabilities by each correlation for sandstone samples
Full size table

Summary and conclusion

In this work, MIP data of 187 sandstone, limestone, and dolomite samples were used to develop a new generalized equation to estimate uncorrected gas permeability. The developed equation uses the smallest pore/throat radius invaded by mercury at 35% mercury saturation, and the sample porosity to calculate its permeability. The proposed equation was validated by calculating the permeabilities of 21 carbonate and 9 sandstone samples. The calculated and measured permeabilities were in good agreement.

Moreover, the proposed equation was compared to other popular equations such as Winland, Katz and Thompson, Rezaee et al., and Gao and Hu. For carbonate samples, the proposed, Winland, and Katz and Thompson equations showed acceptable agreement with the experimentally measured permeabilities. However, our correlation was the most precise one. The superiority of the proposed equation compared with Winland and Katz and Thompson equations is more obvious in low and moderate values of permeability. The Gao and Hu equation highly underestimated the permeability, and hence, it is not suitable for carbonate samples.

In the case of sandstone samples, Rezaee et al. equation underestimated permeability, particularly for high permeability samples. Gao and Hu equation also underestimated permeability, especially for low permeability samples. Although both Winland and Katz and Thompson equations show better accuracies, they generally underestimated the permeabilities of sandstones. For the entire permeability range, the predictions of the proposed equation had better agreement with the experimentally measured data than other tested correlations.