Introduction

The subsurface state of stress depends on three important things: structure of the subsurface (geometry of layers, topology and faults location and orientation), the spatial distribution of rock properties (strength and elastic properties) and the far-field stresses (pore pressure and tectonic stresses). Each of these three components participates in the subsurface state of stress and needs to be addressed and studied in the process of building a mechanical earth model. The mechanical earth model is a numerical representation of the state of stress and rock mechanical properties for a specific stratigraphic section in a field or basin. The model is linked to geologic structure through the local stratigraphy and a 3D seismic cube (Plumb et al. 2000). A case study consists of building a full mechanical earth model on a gas reservoir in Germany; it showed the ability of this model to predict the orientation of the stresses in this reservoir with much accuracy even if it is a faulted reservoir (Henk 2009). Another study performed by Fischer and Henk (2013) concluded that the in situ stresses models predicted by mechanical earth models were calibrated with the field data and they also concluded that those models can give insights to the stress variation in areas where drilling processes not commenced yet. Fischer (2013) also evaluates the capabilities of the mechanical earth model in prediction of the in situ stresses changes and fracture networks in fractured and faulted reservoirs. This study revealed the high ability of the model to display the behavior of the in situ stresses and the natural fractures in the reservoir. A study uses Mohr–Coulomb criteria performed by Adham (2016) to predict the wellbore stability in X field in Sumatra. This study utilized the geomechanical model coupled with chemical and thermal alterations to diagnose the effects of stress changes on wellbore stability issues, and it resulted in mud weight model to avoid wellbore stability issues such as wellbore breakouts and tensile failures. Hydrocarbon production from subsurface reservoirs creates perturbations to the rock and fluid system including fluid saturation, stresses, strains, porosity and permeability, from the obtained results, it was observed the major porosity loss observed in the near wellbore region, and thus, it is advisable to reduce the injection rate in order to enhance the oil production in this area and to avoid any future sanding problems (Lonardelli et al. 2017). Three-dimensional mechanical earth modeling (3D MEM) represents the state of stress in the reservoir under study (magnitude and orientation). The 3D MEM utilizes the best of the available data and knowledge regarding the interaction among the following: subsurface spatial distribution of rock properties (elastic and strength), pore pressure, reservoir geometry and the overburden stress and tectonic and overburden stresses and their influence on in situ stresses. Detailed analysis of the mechanical properties and state of stress in a three-dimensional calibrated model can be applied and utilized in reservoir management, drilling operations and most importantly field development planning (Herwagner and Koutsabeloulis 2011).

3D mechanical earth model is an efficient tool in many areas in reservoir characterization and drilling studies. Three-dimensional mechanical earth model is composed of reservoir geological model, mechanical properties of rocks, magnitude and orientation of in situ stresses (overburden, maximum and minimum) and pore pressure in space. Visualizing the mechanical properties of rocks, in situ stresses and the pore pressure in space (three dimensions) is of utmost importance for a successful field development plans (FDP). Such parameters provide detailed information to many applications such as wellbore stability analysis, directional drilling, hydraulic fracturing, selecting the optimal direction for drilling directional wells and caprock integrity (Janis 2018).

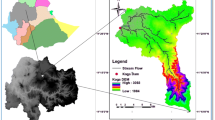
In this study, the 3D mechanical earth model was built using the data from Zubair oilfield. Zubair oilfield is located in the southern part of Iraq (Fig. 1) and discovered in 1947. It is one of the most prolific oilfields in Iraq. Nonproductive time observed almost in most of the wells in Zubair oilfield, especially in the selected wells (Fig. 2) and almost 80% of the total NPT was due to the wellbore stability problems. This 3D MEM will help get a better insight on how stresses are distributed in the entire field. Stress distribution in Zubair oilfield will help in many future development plans such as designing new directional wells and hydraulic fracturing. It also gives an insight on the preexisting faults and predicts their ability to slip via the simulation results.

Fig. 1
figure 1

Location map of Zubair oilfield, southern Iraq (Al-Khafaji 2014)

Full size image
Fig. 2
figure 2

Location map of Zubair oilfield and the selected wells (Al-Khafaji 2014)

Full size image

The 3D MEM is the next step after building the 1D MEM (through properties population), and the 1D MEM was built using three software: Baker Hughes JewelSuite Geomechanics 2017, Schlumberger Techlog 2018 and Paradigm Geolog 18 (Al-Neeamy and Al-Zubaidi 2019). All 1D MEM results were collected and exported to start building the 3D MEM using Schlumberger’s Petrel and Petrel Geomechanics 2018 module and Visage 2018. In addition to 1D MEM data, data from the final geological and drilling reports were used to calibrate and match the 3D MEM results.

Methodology and results

The 3D MEM is based on the 1D MEM for Zubair oilfield that was built by Al-Neeamy and Al-Zubaidi, and the results for the 1D MEM are shown in Fig. 3. The workflow chart for creating the 3D MEM is shown in Fig. 4.

Fig. 3
figure 3

1D MEM mechanical properties (upper), stresses and pore pressure (lower) (Al-Neeamy and Al-Zubaidi 2019)

Full size image
Fig. 4
figure 4

3D MEM workflow chart

Full size image

Constructing the geomechanical grid

Fluid flow inside the reservoir grid has different equations and numerical approaches that are different from the geomechanical modeling. This implies that there should be some modifications to be applied on the reservoir grid before starting the geomechanical analysis and modeling processes. To conduct a full geomechanical analysis, it is of utmost importance to add the overburden, sideburden and underburden to the reservoir grid. Adding those burdens to the reservoir grid will increase the computations time since the grid will be large and composed of more grid blocks. It takes larger times than the time taken by a regular reservoir simulation study. In addition, as an opinion most companies do not conduct a geomechanical analysis due to this reason.

The reservoir grid is constructed using Petrel 2018, and then, the geomechanical grid is built using Reservoir Geomechanical section in Petrel and simulated using Visage 2018.

Constructing the reservoir grid

Constructing the reservoir grid is based on the created geological (static) model. The static model consists of bedding planes (horizons), which are the zones of the area under study. The reservoir model tries to recreate the real geological formations as accurately as possible. Due to the extreme complexity of the real subsurface formations, it is impossible to create an exact and accurate replica to the subsurface formations. The aim of the reservoir grid is to make it ready for simulating the fluid flow.

Building the geomechanical grid

After creating the reservoir grid, the geomechanical section in petrel is responsible in creating the geomechanical grid for the already built reservoir grid. The geomechanical grid is responsible to create the overburden, sideburden and underburden to the reservoir grid. The reason for embedding the reservoir grid inside the geomechanical grid is that any changes in the far-field in situ stresses will not affect the reservoir directly. It is also not realistic to expose the loading conditions and the stresses directly to the reservoir grid and the grid blocks. Stresses changes not dispersed in an equal manner in each block of the reservoir grid, due to this reason as well, it is important to embed the reservoir grid inside the geomechanical grid to get as accurate results as possible. The 2D map showing the location of wells and reservoir grid for the Zubair oilfield is shown in Figs. 5 and 6.

Fig. 5
figure 5

2D map of Mishrif formation showing the location of the wells

Full size image
Fig. 6
figure 6

Zubair oilfield reservoir grid

Full size image

The reservoir grid for the Zubair oilfield without adding any modifications from the aspects of geomechanics done to it is shown in Fig. 6. The final complete geomechanical grid is illustrated in Fig. 7, and the final geomechanical grid for the area surrounding the reservoir is shown in Fig. 8.

Fig. 7
figure 7

Final geomechanical grid (green area reservoir, pink area surrounded geomechanical grid portion)

Full size image
Fig. 8
figure 8

Final geomechanical grid for the area surrounding the reservoir

Full size image

Geomechanical grid parts

As mentioned in the earlier section, the geomechanical grid is responsible for adding the overburden, sideburden, underburden and stiff plates Fig. 9. In this section, a brief introduction to each of these parts will be presented.

Fig. 9
figure 9

Geomechanical grid parts

Full size image

Sideburden

The sideburden portion is the embedded blocks in both directions, i and j. In this study, three grid blocks are added in all directions with refining the intersection area for the reservoir grid. To increase the size of the grid cells, a multiplier of 2 was chosen. It is a low number due to the PC capabilities. A multiplier of 2 means that each cell in the geomechanical grid is larger two times that the reservoir grid cell. This enlargement in cell size is also controlled by the geometric factor (here, chosen as 1.3), which allows the cells to continuously enlarge according to the following formula (Eq. 1).

$$1: \, f: \, f^{2} : \, \ldots \, f^{n - 1}$$
(1)

In the above expression, the “f” refers to the geometric factor and the “n” is the number of grid blocks to be added. To avoid any unnecessary time consumptions and computation steps, it is not necessary that the sideburden is to be refined as the reservoir grid. When applying the boundary conditions and the stresses apply forces on the peripheries of the grid, the underburden and the overburden start to deform in a uniform or non-uniform way. This will lead to the inaccurate results of the pressure calculations. The sideburden in this study is shown in Fig. 10.

Fig. 10
figure 10

Sideburden of the created geomechanical grid

Full size image

In order to project the geomechanical grid cells to the reservoir grid cells, both grids have to be in the same orientations. While building the reservoir grid for Zubair oilfield, the rotation of the reservoir grid is 8°. Therefore, to align the geomechanical grid with the reservoir grid, an option in Petrel Geomechanics section lets you decide the rotation angle depending on the reservoir grid. Therefore, a rotation of 8° is chosen for the geomechanical grid. Both reservoir grid and geomechanical grid orientations (rotation) are shown in Fig. 11a. When applying the same rotations, the software can accurately create the sideburden for the geomechanical grid Fig. 11b.

Fig. 11
figure 11

Rotation angle of both reservoir and geomechanical grids

Full size image

Overburden

The overburden portion of the geomechanical grid is the overlying weight of the reservoir. It extends from the top layer of the reservoir up to the surface. The addition of the overburden allows for an accurate calculation of the overburden (vertical) stress. The process of creating the overburden portion was done in a different way than the sideburden. Petrel Geomechanics section allows to utilize the already created surfaces from the reservoir grid and use them as an overburden. In this study, L. Faris, Gharaf, Dammam, Rutawa and Um-Er-Radhuma surfaces were chosen to be the overburden portion. The surfaces and the converted overburden portion are shown in Fig. 12.

Fig. 12
figure 12

Overburden surfaces and overburden geomechanical portion

Full size image

Zones between surfaces in the geomechanical grid need to divide into subdivisions. Moreover, as done with the sideburden, the geometric factor here is chosen as 1.3. The overburden portion of the geomechanical grid is subdivided into eight divisions. To avoid extra computation steps and time, only the upper/top and the reservoir section is refined to try to get as accurate results as possible.

Underburden

As with the overburden, Petrel Geomechanics section has two options: either to create the underburden from already created geological surfaces or to extend the geomechanical grid to a depth of interest. In this study,by extending the model to a depth of interest, the underburden was added. The underburden is divided into two sections without any further details to the refining process. The underburden extends from below the last geological surface (Al-Rumaila) to the depth of interest and also divided into two divisions without four divisions each. The underburden of the geomechanical grid is shown in Fig. 13.

Fig. 13
figure 13

Underburden geomechanical portion

Full size image

Stiff plates

Stiff plates are similar to hard and incompetent rock mass. Those plates will not distort or deform under any condition whether during compression or tension. This has a great benefit to distribute the pressure in a uniform manner. Without adding those stiff plates, the grid and its parts will deform not in a uniform manner depending on the rock hardness of each of the geomechanical grid portions as shown in Fig. 14. The stiff plates for this study are shown in Fig. 15.

Fig. 14
figure 14

Deformation example of geomechanical

Full size image
Fig. 15
figure 15

Stiff plates of the geomechanical grid

Full size image

Geomechanical properties

Once the process of building the geomechanical grid is finished, the next step is to model the geomechanical properties to each cell of the geomechanical grid. In the previous sections, the geomechanical grid and its portions were created but without assigning any rock types or geomechanical properties. Petrel Geomechanics lets you to assign materials to all the geomechanical grid portions. Those materials are added so to model them into overburden, underburden and sideburden. Those elastic materials are the Young’s modulus (static and dynamic) and Poisson ratio (static and dynamic).

In addition, it depends on the chosen failure criteria. In this study, the Mohr–Coulomb failure criteria are chosen (because its results matched with the available XRMI image logs), and therefore, it is necessary to include the unconfined compressive strength and tensile strength. The results of the mechanical properties are shown in Figs. 16, 17, 18 and 19.

Fig. 16
figure 16

Static and dynamic Young’s modulus

Full size image
Fig. 17
figure 17

Static and dynamic Poisson ratio

Full size image
Fig. 18
figure 18

Unconfined compressive strength

Full size image
Fig. 19
figure 19

Tensile strength

Full size image

In situ stresses

After modeling the stresses in 1D MEM, the next step is to model and distribute those stresses in the created geomechanical grid. This step is done via Visage 2018 simulator. Visage simulator offers the simulation and coupling (coupling between fluid flow and rock mechanics) in different methods: Initialization, one-way coupling and two-way coupling. Due to the limited specification of the PC, one-way and two-way coupling could not be performed. In this study, only the initialization method is utilized.

The initialization method allows the simulation of the initial state of stresses utilizing the ratio between horizontal stress and the vertical without any forwarding in time steps. In one-way coupling,starts at the first time step and compute the pressure and temperature in reservoir simulator (e.g. Eclipse). Then, those values are used to compute the stresses, displacements and strains using the geomechanical simulator (e.g., Visage) without passing to the convergence (matching with the previous results). In two-way coupling, reservoir properties convergence was tested and back those properties to reservoir simulator in order to calculate the pressure and temperature again which will also lead to updating the values of stresses, displacements and strains. This looping process continues until convergence reached and then move to the next time step once convergence reached.

The overburden stress is calculated as described earlier and simulated to the 3D MEM using Visage. (The reader can refer to Visage manual for further explanations on the equations.) After modeling the overburden stress, the two horizontal stresses and the pore pressure modeled in the same way as the overburden stress utilizing the two horizontal to vertical ratios provided. The results of the in situ stresses are shown in Figs. 20, 21, 22 and 23.

Fig. 20
figure 20

Overburden stress

Full size image
Fig. 21
figure 21

Predicted pore pressure (red arrow pointing to the problematic overpressured area)

Full size image
Fig. 22
figure 22

Maximum horizontal stress

Full size image
Fig. 23
figure 23

Minimum horizontal stress

Full size image

Discussion and conclusions

An increase in the pore pressure profile is observed, and it is confirmed with the Poisson ratio and Young’s modulus for the same interval (2130–2160) m in Tanuma formation as shown in Fig. 3 (lower part). Those results make a very good match with the 3D MEM without any variations for both the pore pressure and the Poisson ratio models as illustrated in Figs. 3, 16, 17 and 21.

For the in situ stresses (overburden, maximum and minimum), the modeling results gave a very good match between the 1D and 3D MEMs, and this is due to the same area and data utilized. For the other regions (side- and underburdens), those portions depend solely on the 3D model due to the lack of data in those regions. The increased pore pressure region in Tanuma formation is shown in Fig. 21. Based on those findings and the very good matching between both models (1D and 3D), it will be a reliable starting step for any well-placement and fracturing operations and thus a reliable model for any problem-less future plans.

Three-dimensional mechanical earth model based on one-dimensional mechanical earth model built is for Zubair oilfield. The objective was to diagnose and identify the spatial distribution for the problems appeared in 1D MEM wellbore stability analysis. The 3D MEM captured the spatial distribution of the wellbore stability problems better than the 1D MEM wellbore stability analyses. Initial conditions are also applied to model the 3D MEM to confirm a reliable distribution of the stresses (overburden and the two horizontal stresses). A horizontal isotropy distribution for the mechanical earth model revealed an increase in pore pressure as indicated by the red arrow in the predicted pore pressure model in Tanuma formation. The 3D MEM shows the distribution of the minimum horizontal stress in Zubair oilfield, which is a good starting point in designing a directional drilling and field development plans (FDPs).

The novelty of this work lies in the best utilization and matching between the gathered field data to build the 1D and 3D MEMs and to utilize both models to diagnose and predict future problems to be considered in any field development plans.