Introduction

As oilfields age with time, oil production is associated with increasing water cut which in effect brings tremendous challenges to oil operators. Oil production declines with time, and the high levels of water production increase operational costs as more money have to be spent on storage facilities to contain the produced waters, additives to fight against corrosion, scale formation and bacteria growth among others. These are potential causes of early well abandonment of most wells as most often oil companies cannot break even because of the high cost of production and operation from high water cut wells. Hydrocyclone is an important device, inexpensive as far as separation is concerned, and it capitalizes on the differences in the densities of the flowing media to bring about separation. It has been helpful in industry for more than a century, and it provides an effective, economic and environmentally friendly method to multi-media separation which includes solid–liquid, liquid–liquid, gas–liquid and solid–liquid-gas. Due to its simple and compact size, they can replace the role of large surface separators, both on new and old oil platforms with high water cut histories to cut down cost and make room for more space. The use of liquid–liquid hydrocyclone (LLHC) to separate oil and water was first proposed by Simkin and Olney (1956) and became widely accepted and popular in the 1980s (Schubert 1992; Gomez 2001). Simkin and Olney (1956) studied some of the parameters that can lead to successful and efficient separation of liquid–liquid streams. However, their work did not control the size of the particle droplets in the feed and also there was an air core existing inside the cyclone. Some years later, Burril and Woods (1970) also conducted a study where they considered and controlled the particle droplet sizes in the feed and also got rid of the air core within the cyclone. The earlier works of Simkin and Olney (1956), Burril and Woods (1970), Mahajan and Pai (1977), Sheng et al. (1974) and Hitchon (1959) which showed efficient separation of liquid–liquid streams by the use of the hydrocyclone were an eye opener and urged many researchers such as Colman and Thew (1988), Young et al. (1994) and Belaidi and Thew (2003) among others, to study more into the liquid–liquid hydrocyclonic separation which finds many applications today. LLHC divides the oil–water mixture into two streams as oil-rich stream and water-rich stream. The flow structures within the hydrocyclone play a very important role in the segregation and separation of the fluid particles, and they are impacted by various geometrical and flow parameters. This study seeks to assess and study the flow structures in LLHCs and their influence on separation performance at various design and operational conditions and thereby offer valuable guide to hydrocyclone design and usage in separating oil–water mixture.

As of the new approach of “managing for margin”, there is a focus on recovering the oil reserves before reaching the end of their well’s life at lowest cost. Development of downhole oil–water separation (DOWS) via hydrocyclone separation technology is deemed most attractive for high water cut wells. By reducing the amount of water produced and conveyed to the surface via a downhole hydrocyclone separator and simultaneously injecting water into another formation, operators could optimize the processing capacity at surface and consequently improve the oil production. However, typical installation of downhole hydrocyclone requires at least an electric submersible pump to lift oil to the surface and inject the water back into the formation. Examples are the onshore pilot and applications are in USA, Canada, Venezuela and China (Veil and Quinn 2004). With the complex expensive downhole apparatus setup, space requirement for power generation and difficulty to reenter well for troubleshooting, application in offshore environment is very limited based on literature review.

This study aims to develop flow visualization of the oil/water emulsion within the internal zone of the LLHC separator. The flow visualization has been achieved through numerical simulation to lend understanding to the way oil–water fluid migrates within LLHC device and to show how the flow can affect the efficiency of the separation process. The study considered two different designs of LLHCs, with one inlet and with two inlets. The emulsion concentration has been assumed near the high water cut leading to shutdown as 10% oil–90% water mixture. The study has been carried out with various inlet flow rates. The results have been presented in terms of oil superficial velocity vectors and oil superficial velocity streamlines within the LLHCs, phase distributions and separation efficiency.

LLHC geometry and operation

A schematic diagram of a LLHC is shown in Fig. 1. It is made up of sets of cylindrical and conical sections. The upper cylindrical part is closed at the top by a cover, through which is the vortex finder for the lighter fluid (oil) to exit. The pressurized produced fluid is introduced into the top cylindrical portion of the LLHC through one or more tangential inlets, and this causes the fluids to spin and rotate within the device. As the fluid spirals down against the walls of the LLHC, the reducing cross-sectional area of the cyclone causes a rise in the fluid angular velocity and the centrifugal force. The centrifugal force developed accelerates the settling rate of the fluid particles thereby separating them according to size, shape and difference in density. The swirling of the fluid mixture (developing the centrifugal force) together with the action of the drag force as shown in Fig. 2, cause the lighter fluid (oil) to migrate towards the core of the LLHC with the heavier fluid (water) spinning to the outside walls of the LLHC (Wills and Napier-Munn 2006; Gomez et al. 2002; Bowers et al. 2000).

Fig. 1
figure 1

LLHC hydrodynamic flow behaviour (Gomez et al. 2002)

Full size image
Fig. 2
figure 2

Forces acting on an orbiting fluid particle in the hydrocyclone (Wills and Napier-Munn 2006)

Full size image

The separation mechanism of oil and water using LLHC is governed by Stokes law, and this is realized in the difference between centrifugal force created through the spinning of the fluid and the drag force on the droplet particles as already depicted in Fig. 2. Since the parts of the cyclone separator do not move during operation, separation is brought about by the development of high centrifugal forces by the help of its geometric design (Ogunsina and Wiggins 2005).

It is interesting to note that, the centrifugal force causes the flow pattern within the LLHC to consist of two helical motions in the same circular direction. There is therefore the creation of forced vortex near the centre of the LLHC and a free-like vortex towards the walls of the LLHC. It is the latter vortex which carries the heavier fractions of the fluid downward to the underflow outlet, with the former vortex carrying the lighter fractions of the fluid in reverse direction to the overflow outlet. At times, there are occurrences of some fluid recirculation at the top part of the hydrocyclone and this is attributed to high swirling rate encountered at the inlet region. The recirculation zones tend to have long residence time with very low axial velocity which can have adverse effect on separation performance. These zones, however, subside as the flow migrates to the low-angle tapering section of the LLHC (Gomez et al. 2002).

The reverse flow in the LLHC is due to the high swirling intensity at the inlet which causes the pressure to be high near the cyclone wall and very low towards the core region. Thus, the works of Osei et al. (2016) and Inès et al. (2015) showed that the pressure within the cyclone decreases radially from the cyclone wall to the core. By ensuring a higher pressure at the underflow outlet than that at the overflow, the lighter fraction (oil) concentrated at the core is forced to flow countercurrent to the main flow (Gomez et al. 2002; Bowers et al. 2000). Sina et al. (2012) also illustrated how the swirling motion of the fluid at the conical part of the hydrocyclone supports the migration of the oil droplets to the centre of the hydrocyclone. Oil droplets that get into the reverse flow region at the core of the cyclone are carried upward and exit the vortex finder as the oil fraction. By knowing the oil droplet path lines within the hydrocyclone, it is easier to find out those droplets that will make or will not make their way to the upward reversal flow. Those that fail to get to the reverse flow core will remain in the continuous phase and swirl down the walls of the cyclone to be separated as water leg. As the flow in the conical section moves downward, it continually loses oil, because the larger oil droplets move to the core of the cyclone enriching the oil leg which will later be carried by the reversal flow. It is not possible to achieve 100% separation of oil and water in a LLHC as some oil will escape with the water fraction and some water also produced with the hydrocarbon fraction. However, the separation purity can be enhanced by connecting several hydrocyclones in series. Several hydrocyclone separators can also be connected in parallel to handle large volumes of feed (Ogunsina and Wiggins 2005). The division between upward flow carrying the lighter fraction (oil) and downward flow carrying the heavier fraction (water) determines the midsection when a classification (separation) curve is made. The centrifugal force is mostly responsible for the heavier side of the classification curve (Delgadillo and Rajamani 2007).

Numerical study

Numerical simulations were performed using ANSYS 15 commercial software. Gambit, a preprocessing software, was used to model the physical geometry of the LLHC types presented in Fig. 3. The LLHCs have an angle of 20° at the upper conical section and 7.6° at the lower conical section which make them different from other LLHCs such as those from Colman and Thew (1988), Young et al. (1994) and Belaidi and Thew (2003) mostly used in liquid–liquid separation. These features are very important as it is at these sections where most of the fluid segregation happens. Thus, most of the separation occurs at tapering sections of the hydrocyclone, most especially, at the latter section. As ANSYS-CFD provides the widest range of sophisticated turbulence and physical models to accurately simulate, the general CFD in FLUENT solver was utilized to simulate the current complex two component flow, with high turbulence. The created geometries were imported into ANSYS—FLUENT CFD for meshing, setting up of the boundary conditions and select the appropriate turbulence model suiting the current simulation by CFD. In order to ensure that proper mesh that could result in better separation process for the LLHC oil–water modelling, a mesh independency study was carried out based on the average oil volume recovered at the overflow (since it is at this point that the quantity of oil in the feed that has been separated could be determined) to select the optimized number of elements that would give better and effective solution for the studied LLHCs. A 3D computational model was selected for the meshing of the LLHC because it provides results that properly match experimental data, as recommended by Wang et al. (2011). Different meshes with different number of elements (115,717, 186,170, 190,703 and 208,436) (see Fig. 4) were created.

Fig. 3
figure 3

LLHC geometry: a single inlet; b double inlet

Full size image
Fig. 4
figure 4

Mesh independency: a single inlet; b double inlet

Full size image

The multiphase mixture model in ANSYS-CFD was used to model the oil–water multiphase flow in the LLHCs because the oil–water phases may interact strongly with each other within the cyclone during swirling. The water was the primary (continuous) phase with the oil being the secondary (dispersed) phase in the interpenetrating continuum. The dispersed oil phase had volume fraction of 0.1 signifying high water cut. However, it was significant and needed full consideration of the oil–water phase interaction. Inlet flow rate ranged between 0.5–1.0 m3/h. The SIMPLE algorithm was utilized to achieve pressure–velocity coupling between the continuity and momentum equations (Murthy and Bhaskar 2012; Mousavian et al. 2009). All the gradients were discretized based on the least squared cell-based approach. PRESTO scheme was selected as it provides better estimation for high speed swirling flows, and flows in strongly curved domains (Murthy and Bhaskar 2012; Mousavian et al. 2009). The equations for momentum, volume fraction and kinetic energy were discretized using QUICK as it is a higher-order discretization than the first- and second-order schemes and gives better and accurate results for rotational swirling flows (Murthy and Bhaskar 2012; Mousavian et al. 2009). The first-order discretization is associated with increasing discretization error and often produces misleading results in cyclone separator simulations (Utikar et al. 2010). As regards the turbulence model, Reynolds stress model (RSM) was used because it is suited for complex flows and is more accurate for swirling and rotational flow. It accounts for streamline curvature effects, swirling, rotation and rapid changes in strain rate as well as capturing the anisotropic character of the turbulence in the LLHC. It has higher ability of accurately predicting complex flows in hydrocyclone (Wang et al. 2011; Zhang et al. 2011; Hai-fei et al. 2010). The Reynolds stress turbulence model can be expressed as follows (Osei et al. 2016; Hai-fei et al. 2010; Bao-yu et al. 2014):

$$\frac{\partial }{\partial t}\left( {\rho \overline{{u_{i}^{'} u_{j}^{'} }} } \right) + \frac{\partial }{{\partial x_{k} }}\left( {\rho u_{k}^{'} \overline{{u_{i}^{'} u_{j}^{'} }} } \right) = P_{ij} + D_{Tij} + \varPhi_{ij} - \varepsilon_{ij} + F_{ij}$$
(1)

where Pij is the stress production term; DTij is the turbulent diffusion term; Φij is the pressure-strain term; εij is the viscosity diffusion term; and Fij is the rotation production term. They are defined as follows:

$$P_{ij} = - \rho \left( {\overline{{u_{i}^{'} u_{k}^{'} }} \frac{{\partial u_{j} }}{{\partial x_{k} }} + \overline{{u_{j}^{'} u_{k}^{'} }} \frac{{\partial u_{i} }}{{\partial x_{k} }}} \right)$$
(2)
$$D_{Tij} = - \frac{\partial }{{\partial x_{k} }}\left[ {\rho \overline{{u_{i}^{'} u_{j}^{'} u_{k}^{'} }} + \overline{{p\left( {\delta_{kj} u_{i}^{'} + \delta_{ik} u_{j}^{'} } \right)}} } \right]$$
(3)
$$\varPhi_{ij} = \left( {\overline{{\frac{{\partial u_{i}^{'} }}{{\partial x_{j} }} + \frac{{\partial u_{j}^{'} }}{{\partial x_{i} }}}} } \right)$$
(4)
$$\varepsilon_{ij} = - 2\mu \overline{{\frac{{\partial u_{i}^{'} }}{{\partial x_{k} }}\frac{{\partial u_{j}^{'} }}{{\partial x_{k} }}}}$$
(5)
$$F_{ij} = - 2\rho \varOmega_{k} \left( {\overline{{u_{j}^{'} u_{m}^{'} }} \varepsilon_{ikm} + \overline{{u_{i}^{'} u_{m}^{'} }} \varepsilon_{jkm} } \right)$$
(6)

The boundary conditions are presented in Table 1, whereas the properties of the primary phase (water) and the secondary phase (oil) used in the oil-in-water simulation are given in Table 2.

Table 1 Boundary conditions for the oil–water simulation
Full size table
Table 2 Material specification of primary and secondary phases
Full size table

Results and discussion

The flow structure within the LLHC has been investigated through computational flow visualization. The velocity vectors inside the two hydrocyclone types, 30 mm chamber with one inlet and dual inlets, were established for better indication of the flow mechanism inside the cyclone. The axial velocities at two different axial locations were computed and compared with the Chang and Dhir (1994) axial velocity data to validate the axial flow dynamics of the work. The axial velocity magnitude at the axis of the hydrocyclone plays a key role in the upward transportation of the oil via the overflow finder. From Fig. 5, there is an agreement between the results from this study and that of Chang and Dhir (1994). The magnitude of the velocity at the core of the hydrocyclone gives a good agreement.

Fig. 5
figure 5

Validation of axial velocity profile: az = 20 mm and bz = 40 mm

Full size image

Figure 6 presents the oil superficial velocity vectors on a central vertical plane that divides the LLHC into exactly two halves. The oil–water mixture inflow rate was 0.5 m3/h. The speed of flow to the hydrocyclones is greatest at the inlet(s) and decreases as the flow migrates to the lower sections of the cyclone. The high fluid flow at the entry is significant for centrifugal acceleration of the fluid particles in order to ensure fluid separation. However, as the fluid spirals against the cyclone walls, it loses energy and the fluid acceleration drops at the lower section of the cyclone. By the time the fluid migrates to the second conical section of the cyclone, most of the separation has been achieved. Moreover, it can be noted from the figures that, fluid velocity decreases radially from the walls of the cyclone to its core. This effect may be attributed to the spinning intensity and pressure which decrease as the fluid moves towards the centre of the cyclone as shown by the works of Inès et al. (2015) and Al-Kayiem et al. (2014).

Fig. 6
figure 6

Oil superficial velocity vectors at 0.5 m3/h using 10% oil–90% water mixture: a single inlet LLHC; b dual inlet LLHC

Full size image

Figure 6 shows the oil superficial velocity vectors in both the single inlet and dual inlet hydrocyclones, from the inlet down to the tapering section of the cyclone where most of the separation takes place. The developed centrifugal force causes the lighter fluid fraction (oil) to settle and be concentrated at the centre of the LLHC with the heavier fluid fraction (water) segregating and concentrating in the vicinity of the LLHC walls. The purpose of the inlet chamber which is to stabilize the flow, after entry from the inlet, was defeated and the flow swirled down in a meandering manner. The concentrated oil core in the single inlet LLHC shows a clear indication of wavering velocity vectors moving towards the overflow outlet. The velocity vectors in the case of the dual inlet hydrocyclone, however, were symmetrical with no wavering oil core at the axis of the LLHC. The velocity was greatest near the walls and decreased towards the centre.

In Fig. 7, when the fluid inflow rate was changed to 1.0 m3/h, similar flow structure of the oil velocity vectors was achieved, but in this case, with greater impact on the flow information. Relatively higher velocities were recorded in the cyclone, and the flow was more turbulent. The single inlet LLHC experienced the wavering oil core region with the dual inlet having the straight and centralized inner oil core region. The undulating nature of the flow in the single inlet hydrocyclone amid the turbulent flow has the tendency to disturb the classification of the oil–water droplets and thereby affect the separation efficiency. The pattern of the flow structure within the LLHC, oil–water segregation and concentrations inside the cyclone is therefore influenced by the number of the tangential inlets.

Fig. 7
figure 7

Oil superficial velocity vectors at 1.0 m3/h using 10% oil–90% water mixture: a single inlet LLHC; b dual inlet LLHC

Full size image

The earlier works of Osei et al. (2016) showed how the inner flow structure could affect the axial and tangential velocities and the pressure distributions within the cyclone. The wavering nature of the flow observed in the single inlet hydrocyclone affected the separation performance from the single inlet hydrocyclone. Most of the water droplets near the vicinity of the reverse flow boundary were carried along with the inner flow core that moves upward to the overflow exit causing some water to escape with the oil-rich fraction. The unwavering nature of the flow structure realized in the dual inlet hydrocyclone, however, assisted separation as the two fluids could easily be segregated into the oil-rich core (inner) and water-rich core (outer).

Due to the swirling nature of flow within the LLHC, recirculation often tends to occur. This also has adverse effect on the separation process of the hydrocyclone. In order to better visualize the recirculation zones existing in both inlet cases, Figs. 8 and 9 were generated. Many fluid recirculation regions were observed in the single inlet LLHC, and some spread over large areas within the LLHC. However, virtually no recirculation zones were realized in the case of the dual inlet LLHC.

Fig. 8
figure 8

Oil velocity streamlines at 0.5 m3/h using 10% oil–90% water mixture: a single inlet LLHC; b dual inlet LLHC

Full size image
Fig. 9
figure 9

Oil velocity streamlines at 1.0 m3/h using 10% oil–90% water mixture: a single inlet LLHC; b dual inlet LLHC

Full size image

The occurrence of recirculation zones affected the segregation of the oil and water droplets. Some droplets were kept in constant circulation which increased their residence time. The end effect is that, such droplets hardly go through the classification/segregation process happening within the LLHC and thereby escaped unclassified to either of the two outlets. The single inlet LLHC will therefore have most unclassified droplets which will affect the efficiency of the separation process. When the oil–water mixture inflow rate was increased from 0.5 to 1.0 m3/h, more recirculation zones were observed in the single inlet LLHC. Another negative effect of increasing recirculation is droplet breakups. Hydrocyclone separation is favored by increasing oil droplet size. By this fact, minimum or no recirculation is highly recommended as observed in the dual inlet LLHC.

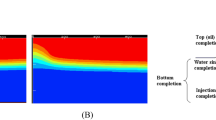
Figure 10 presents the phase distribution of the continuous phase within the LLHCs at different axial locations. The concentration and pressure of water are immense at the walls of the cyclone. This is as a result of its density and the swirling nature of the flow which segregates the oil–water mixture. At the core of the LLHCs, the water concentrations are minimum giving way for more oil to concentrated, so that it can be carried to the overflow.

Fig. 10
figure 10

Continuous phase concentration/pressure within the LLHCs at different axial locations: a single inlet; b dual inlet

Full size image

The separation efficiency achieved from the use of the two LLHCs indicated significant performance from the use of the dual inlet LLHC. This was calculated by dividing the total oil volume obtained at the overflow to the total oil volume at the inlet of the LLHCs. An efficiency of 82.3% was obtained from the dual inlet LLHC as against 73.7% from the single inlet LLHC at 0.5 m3/h. The treatment of the oil–water feed at 1.0 m3/h also showed a great performance from the dual inlet LLHC which produced separation efficiency of 93.6% as against 88.5% for the use of the single inlet LLHC (Fig. 11).

Fig. 11
figure 11

Separation efficiency of the LLHCs at 0.5 m3/h and 1.0 m3/h

Full size image

Conclusion

The flow structure within hydrocyclone is influenced by the number of inlets to the cyclone. Wavering and unsymmetrical flow structures result when the feed is introduced from only one inlet of the cyclone. With one inlet, the flow is realized to have several recirculation zones which affect the performance of the cyclone device as some fluid droplets remained unclassified. With dual inlets, at 180° shift, a uniform flow structure, void of recirculation ensured easy segregation of oil/water droplets thereby improving separation. The dual inlet LLHC outperformed the single inlet LLHC, and the former is therefore a promising device to alleviate the excessive water production from wells and improve the economics of oil production.