Introduction

Knowledge of transport phenomena in porous media is essential in several disciplines (Scheidegger 1957; Chavent and Jaffre 1986; Bear and Yehuda 1990; Civan 2011 ) including soil science, groundwater hydrology, petroleum engineering, storage of energy byproducts in deep geological formations, and biomedical engineering among others (Greenkorn 1983; Weir et al. 1996; Acar et al. 1997; Khaled and Vafai 2003; Pinder and Gray 2008; Kim et al. 2014). A sub-problem of transport in porous media is two-phase immiscible flow in geological formations. It is important to understand and predict the behavior as it is significant in the remediation of hydrocarbon polluted sites (Hunter 1981; Bruell et al. 1992, Wise 2000) and in oil recovery (Amba et al. 1964; Haroun and Chilingar 2009; Al Shalabi et al. 2012a; Chillingar and Haroun 2014) in reservoirs.

Electrokinetic (EK) phenomena are among the oldest concepts in surface and colloid science (Wall 2010). The term “electrokinetics” refers to the motion of small particles in fluids that is induced by an electrical field (Chillingar and Haroun 2014). The principles of electrokinetic phenomena have been applied in various areas such as soil and groundwater remediation (Wise 2000; Chillingar and Haroun 2014), material science (Llorente et al. 2014), biology and medicine (Abramson 1934), water treatment (Hayes 2012; Peraki et al. 2016), and many others. In particular, EK has been used for decontamination of hydrocarbon polluted soils (Hunter 1981; Bruell et al. 1992, Wise 2000), which involves: (1) electro-migration, (2) electrophoresis, and (3) electro-osmosis processes.

EK has also been proposed for oil recovery in relatively recent years (Chillingarian 1952; Amba et al. 1964; Haroun and Chilingar 2009; Wittle and Hill 2006; Wittle et al. 2011; Ghosh et al. 2012; Rehman and Meribout 2012; Hashmi and Ghosh 2015). The electrically enhanced oil recovery method (EEOR) is reported to be capable of increasing the oil production in environments that other enhanced oil recovery (EOR) techniques are unable to produce (Wittle and Hill 2006; Wittle et al. 2011). The basic premise of the EEOR method is the successful application of the principles of electrokinetics. As in the case of soil decontamination, when applying electrokinetic principles in EEOR, the main involved mechanisms are hypothesized to be: (1) electro-migration, (2) electrophoresis, and (3) electro-osmosis (Wittle and Hill 2006; Wittle et al. 2011; Ghazanfari 2013). Joule heating of the reservoir due to the applied electrical field and electrochemically enhanced reactions are also theorized to contribute to the oil recovery (Wittle and Hill 2006; Wittle et al. 2011; Ghazanfari 2013). Electro-osmosis can initiate flow of water, exerting a viscous drag on the oil phase, which results in an increase in the oil production (Cassagrande 1952; Chillingar et al. 1968; Chillingar and Haroun 2014). In addition, the electrically induced chemical reactions are hypothesized to cause the so-called “cold cracking” of the complex hydrocarbon compounds into simpler compounds reducing the viscosity of the oil and increasing its mobility (Wittle and Hill 2006; Ghazanfari 2013).

In EEOR method, the electrical field (direct current) is directly applied to the reservoir between a cathode (usually installed in the production well), and anodes (usually installed in injection wells) (Wittle et al. 2011) as shown in Fig. 1. Typically, the well configuration is such that a single well is used for injection (anode) and an array of production wells (cathodes) are placed around the injection well (Wittle and Hill 2006; Wittle et al. 2011).

Fig. 1
figure 1

Schematic showing field operation of combined EEOR and water flooding

Full size image

The EEOR method has been tested both at the laboratory scale (Amba et al. 1964, 1965; Haroun and Chilingar 2009; Al Shalabi et al. 2012a) and in the field (USA and Canada) with relatively encouraging results (Wittle and Hill 2006; Wittle et al. 2011). In the field, EEOR is not usually used as a sole oil recovery method because of the insufficient oil that it produces. However, when combined with water flooding, it has been found in laboratory experiments (Aggour and Muhammadain 1992; Al Shalabi et al. 2012b) and in the field (Wittle and Hill 2006; Wittle et al. 2011) to improve the oil recovery. Although a limited number of laboratory and field investigations have demonstrated the potential promise of the EEOR method, further investigation is necessary to better understand the fundamentals of the method and the importance of different parameters/processes critical to the transport phenomena controlling the oil production. Mathematical models can facilitate investigating the feasibility of oil recovery under different reservoir conditions and to provide a fundamental understanding of two-phase flow under reservoir conditions (Amba et al. 1964; Killough and Gonzalez 1986; Chillingar and Haroun 2014).

The main objective of this study was to use numerical tools to investigate the feasibility of the EEOR method and to provide insight into the important parameters that contribute to the flow and oil production in this method. Specifically, the two-phase immiscible flow under coupled pressure and electrical gradients involved in EEOR combined with water flooding was investigated. The paper is structured as follows: “Methodology” section provides the methodology used to develop the model, which includes the set of governing equations, numerical solution scheme used to solve the set of governing equations, steps followed for numerical solution, and the description of the numerical-experiment set-up. Section “ Results and discussion” presents a sensitivity analysis of the model, the results of the numerical simulation, and discussion on the significance of different parameters involved in the method. Finally, “Conclusions” section provides conclusions based on the analysis of the results.

Methodology

The set of governing equations underpinning the numerical model of the EEOR combined with water flooding are provided in “Governing equations” section. First, the governing equations for only water flooding are presented and subsequently the governing equations for application of the electrical field are introduced. Details of the numerical solution scheme are provided in “Numerical solution scheme” section. The steps followed for the numerical simulation are presented in “Simulation steps” section. Finally, description of the numerical-experiment set-up is provided in “Numerical-experiment set-up” section.

Governing equations

The first step is simulation of the effects of water flooding on pressure and fluid saturations during oil production, without application of electrical field. To simplify the equations involved in the two-phase flow, the following assumptions were made: the two phases are considered immiscible and incompressible with no exchange of species between them, the rock matrix is assumed to be incompressible, and the total flow rate of oil and water are assumed to remain constant.

Flow due to applied pressure gradient

The governing equation describing two-phase flow due to an applied pressure gradient is the fluid continuity equation (Aziz and Settari 1979; Chen et al. 2006; Arnes et al. 2007; Islam et al. 2010):

$$\begin{array}{*{20}c} {\frac{{\partial \left( {\varphi \rho_{\alpha } S_{\alpha } } \right)}}{\partial t} + {\mathbf{\nabla }} \cdot \left( {\rho_{\alpha } \cdot {\mathbf{v}}_{{\varvec{\upalpha}}} } \right) = q_{\alpha } } \\ \end{array}$$
(1)

where φ is the porosity of the porous medium, ρα is the density of the phase α, Sα is the saturation of phase α, vα is the flow velocity of phase α, and qα is the source/sink term. Assuming the density of the phase is constant, we get:

$$\begin{array}{*{20}c} {\frac{{\partial \left( {\varphi S_{\alpha } } \right)}}{\partial t} + {\mathbf{\nabla }} \cdot {\mathbf{v}}_{{\varvec{\upalpha}}} = \frac{{q_{\alpha } }}{{\rho_{\alpha } }} } \\ \end{array}$$
(2)

For low flow velocities, Darcy’s law is expressed as:

$$\begin{array}{*{20}c} {{\mathbf{v}}_{{\varvec{\upalpha}}} = - {\varvec{\uplambda}}_{{\varvec{\upalpha}}} \cdot \left( {{\mathbf{\nabla }}P_{\alpha } + \rho_{\alpha } g{\mathbf{\nabla }}z} \right) } \\ \end{array}$$
(3)

where λα is the mobility of phase α, Pα is the pressure of phase α, g is the gravitational constant, and z is the spatial coordinate in the upward vertical direction. The phase mobility is defined as (Dake 1978; Arnes et al. 2007):

$$\begin{array}{*{20}c} {{\varvec{\uplambda}}_{{\varvec{\upalpha}}} = \frac{{{\mathbf{K}} k_{r\alpha } }}{{ \mu_{\alpha } }} } \\ \end{array}$$
(4)

where K is the absolute permeability tensor of the porous medium, krα and μα are relative permeability and dynamic viscosity of phase α, respectively. The set of empirical expressions for the relative permeability of water and oil that are used in this study are (Brooks and Corey 1964):

$$\begin{array}{*{20}c} {k_{\text{rw}} = \left( {S_{\text{e}} } \right)^{{\frac{2 + 3\lambda }{\lambda }}} } \\ \end{array}$$
(5)
$$\begin{array}{*{20}c} {k_{\text{ro}} = \left( {1 - S_{\text{e}} } \right)^{2} \left( {1 - S_{\text{e}}^{{\frac{2 + \lambda }{\lambda }}} } \right)} \\ \end{array}$$
(6)

where λ is the pore-size distribution index and Se is the effective saturation of water expressed as (Greenkorn 1983):

$$\begin{array}{*{20}c} {S_{\text{e}} = \frac{{S_{\text{w}} - S_{\text{wc}} }}{{1 - S_{\text{or}} - S_{\text{wc}} }} } \\ \end{array}$$
(7)

where Sor is the irreducible oil saturation (i.e., lowest oil saturation that can be achieved) and Swc the connate water saturation (i.e., water trapped in the pores of rock during rock formation). The viscous coupling effect between the two phases in the pressure-driven flow is considered as negligible and therefore is not incorporated in the model.If we substitute Eq. 3 into Eq. 2 and assume horizontal flow, we get:

$$\begin{array}{*{20}c} {\frac{{\partial \left( {\phi S_{\alpha } } \right)}}{\partial t} - {\mathbf{\nabla }} \cdot \left( {{\varvec{\uplambda}}_{{\varvec{\upalpha}}} \cdot {\mathbf{\nabla }}P_{\alpha } } \right) = \frac{{q_{\alpha } }}{{\rho_{\alpha } }} } \\ \end{array}$$
(8)

The phase pressures can be replaced by a global pressure, P, if we introduce the fractional flow function, fα, and assume that at reservoir conditions the viscous forces dominate the effect of the capillary forces (Arnes et al. 2007):

$$\begin{array}{*{20}c} {P = P_{\text{o}} - P_{\text{c}} } \\ \end{array}$$
(9)
$$\begin{array}{*{20}c} {f_{{\varvec{\upalpha}}} = {\varvec{\uplambda}}_{{\varvec{\upalpha}}} \cdot \left( {{\varvec{\uplambda}}_{{{\mathbf{tot}}}} } \right)^{ - 1} } \\ \end{array}$$
(10)
$$\begin{array}{*{20}c} {{\varvec{\uplambda}}_{{{\mathbf{tot}}}} = {\varvec{\uplambda}}_{{\mathbf{w}}} + {\varvec{\uplambda}}_{{\mathbf{o}}} } \\ \end{array}$$
(11)

where Po is the pressure of the oil phase, and Pc is a saturation-dependent complementary pressure expressed as (Arnes et al. 2007; Ghazanfari 2013):

$$\begin{array}{*{20}c} {{\mathbf{P}}_{{\mathbf{c}}} \left( {S_{\text{w}} } \right) = \mathop \int \limits_{1}^{{S_{\text{w}} }} {\mathbf{f}}_{{\mathbf{w}}} \left( \beta \right)\frac{{\partial P_{\text{cow}} }}{{\partial S_{\text{w}} }}\left( \beta \right){\text{d}}\left( \beta \right) } \\ \end{array}$$
(12)

where

$$\begin{array}{*{20}c} {P_{\text{cow}} = P_{\text{o}} - P_{\text{w}} } \\ \end{array}$$
(13)

Combing Eqs. 8 and 10, and considering the fact that the introduced fractional flow function allows taking into account only the part of the global pressure that is attributed to the specific phase α, we get:

$$\begin{array}{*{20}c} {\frac{{\partial \left( {\phi S_{\alpha } } \right)}}{\partial t} - {\mathbf{\nabla }} \cdot \left( {{\mathbf{f}}_{{\varvec{\upalpha}}} \cdot {\mathbf{\nabla }}P} \right) = \frac{{q_{\alpha } }}{{\rho_{\alpha } }} } \\ \end{array}$$
(14)

In most cases, the saturation of water is primarily used, so the equation becomes:

$$\begin{array}{*{20}c} {\frac{{\partial \left( {\phi S_{\text{w}} } \right)}}{\partial t} - {\mathbf{\nabla }} \cdot \left( {{\mathbf{f}}_{{\mathbf{w}}} \cdot \nabla P} \right) = \frac{{q_{\text{w}} }}{{\rho_{\text{w}} }} } \\ \end{array}$$
(15)

Equation 15 is called the saturation equation. The saturation of oil is calculated using:

$$\begin{array}{*{20}c} {S_{\text{w}} + S_{\text{o}} = 1 } \\ \end{array}$$
(16)

The pressure equation is given by the summation of the saturation equations (Eq. 14) for oil and water combined with Eq. 16 as:

$$\begin{array}{*{20}c} { - \nabla \cdot \left( {{\varvec{\uplambda}}_{{{\mathbf{tot}}}} \cdot {\mathbf{\nabla }}P} \right) = \frac{{q_{\text{w}} }}{{\rho_{\text{w}} }} + \frac{{q_{\text{o}} }}{{\rho_{\text{o}} }} } \\ \end{array}$$
(17)

To make the pressure equation complete, appropriate boundary conditions must be prescribed.

Flow due to applied electrical gradient

The electro-osmotic (EO) velocity of phase α in a surface-charged porous medium is given by the Helmholtz–Smoluchowski equation as (Smoluchowski 1914):

$$\begin{array}{*{20}c} {{\mathbf{v}}_{{{\text{e}},{\varvec{\upalpha}}}} = - \frac{\varepsilon \xi }{\mu }{\mathbf{\nabla }} \cdot \varPhi_{{\varvec{\upalpha}}} } \\ \end{array}$$
(18)

where ε is the permittivity of the medium, ξ is the zeta potential, and Φ is the applied electrical potential.

The electro-osmotic permeability coefficient of the medium is defined as (Ghazanfari 2013):

$$\begin{array}{*{20}c} {{\mathbf{k}}_{{{\mathbf{eo}}}} = - \frac{\varepsilon \xi }{\mu } } \\ \end{array}$$
(19)

For two-phase flow (oil and water), the electro-osmotic velocity of a fluid in a surface-charged porous medium can be expressed as an extension of the Helmholtz–Smoluchowski equation (see Eq. 18) (Ghazanfari 2013; Chillingar and Haroun 2014):

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{{{\mathbf{e,w}}}} } \\ {{\mathbf{v}}_{{{\mathbf{e,o}}}} } \\ \end{array} } \right] = - {\mathbf{k}}_{{{\mathbf{eo}}}} \cdot \left[ {\begin{array}{*{20}c} {k_{\text{er,ww}} } &\quad {k_{\text{er,wo}} } \\ {k_{\text{er, ow}} } &\quad {k_{\text{er,oo}} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{\mathbf{\nabla }}\varPhi_{\text{w}} } \\ {{\mathbf{\nabla }}\varPhi_{\text{o}} } \\ \end{array} } \right] } \\ \end{array}$$
(20)

where ker is the relative electro-osmotic permeability.

The viscous coupling between the two phases is considered through the off-diagonal relative electro-osmotic permeability coefficients in Eq. 20. In most of the reservoirs, the oil phase is non-polar; hence, application of an electrical field does not generate a flow in the oil phase (Ghazanfari et al. 2014). Therefore, ker,ow and ker,oo coefficients are set to zero, and the applied electrical gradient is set to be the same for both phases (Φ) due to the random distribution of fluids in the reservoir (Ghazanfari 2013; Chillingar and Haroun 2014). In this study, the coefficients of relative electro-osmotic permeability (ker,ww and ker,wo) are estimated using an empirical correlation developed from available experimental data (Ghazanfari 2013; Chillingar and Haroun 2014).

The pressure and saturation equations (Eqs. 15 and 17) are modified to accommodate the flow generated due to the applied electrical gradient as:

$$\begin{array}{*{20}c} {\frac{{\partial \left( {\phi S_{\text{w}} } \right)}}{\partial t} - {\mathbf{\nabla }} \cdot \left( {{\mathbf{f}}_{{\mathbf{w}}} \cdot \nabla P + {\mathbf{k}}_{{{\mathbf{eo}}}} k_{\text{er,ww}} \cdot {\mathbf{\nabla }}\varPhi } \right) = \frac{{q_{\text{w}} }}{{\rho_{\text{w}} }} } \\ \end{array}$$
(21)
$$\begin{array}{*{20}c} { - \nabla \cdot \left[ {{\varvec{\uplambda}}_{{{\mathbf{tot}}}} \cdot {\mathbf{\nabla }}P + {\mathbf{k}}_{{{\mathbf{eo}}}} \left( {k_{\text{er,ww}} + k_{\text{er,wo}} } \right) \cdot {\mathbf{\nabla }}\varPhi } \right] = q } \\ \end{array}$$
(22)

In order to determine the voltage distribution in the medium, first Archie’s law (Archie 1942; Bassiouni 1994; Grattoni and Dawe 1996; Ferre et al. 1998) is used to estimate the total electrical resistivity as:

$$\begin{array}{*{20}c} {R_{t} = \frac{{F R_{\text{w}} }}{{S_{\text{w}}^{n} }} } \\ \end{array}$$
(23)

where F is the formation resistivity factor, Rw is the electrical resistivity of water, Sw is the water saturation, and n is a coefficient whose value can be determined from laboratory measurements, and is close to 2 for sandstone reservoirs (Bassiouni 1994).

Although the total resistivity depends also on other parameters (e.g., temperature and particle size distribution), the effect of saturation dominates over other parameters (Bai et al. 2013). The formation resistivity factor is controlled mainly by porosity and tortuosity, but tortuosity is almost impossible to measure experimentally. Based on laboratory measurements of F and φ on core samples, the following empirical relationship is suggested in the literature (Archie 1942):

$$\begin{array}{*{20}c} {F = \varphi^{ - m} } \\ \end{array}$$
(24)

An empirical equation, similar to Archie’s, that provides a better fit is (Winsauer 1952):

$$\begin{array}{*{20}c} {F = \alpha \varphi^{ - m} } \\ \end{array}$$
(25)

where α is the coefficient of cementation and m is the exponent of cementation. Both coefficients are determined experimentally through F − φ data. An extensive collection of F − φ data was gathered (1833 sandstone samples) by Timur et al. 1972 and analysis of the data resulted in the Chevron formula:

$$\begin{array}{*{20}c} {F = 1.13\varphi^{ - 1.73} } \\ \end{array}$$
(26)

The equation expressing charge conservation for steady state current is (Avants et al. 1999):

$$\begin{array}{*{20}c} {{\mathbf{\nabla }} \cdot {\mathbf{i}} = 0 } \\ \end{array}$$
(27)

where i is the current density.

Per Ohm’s law (Avants et al. 1999; Alshawabkeh 2001):

$$\begin{array}{*{20}c} {{\mathbf{\nabla }} \cdot {\mathbf{i}} = \frac{1}{\rho }{\mathbf{\nabla }} \cdot {\mathbf{E}} } \\ \end{array}$$
(28)

where ρ is the average resistivity of the medium (i.e., reservoir) and E the applied electrical gradient (∇Φ). The average resistivity is not the true resistivity, rather is a weighted average of the resistivity of the reservoir and the various materials that the current encounters (Herman 2001). Since an average resistivity is assumed for the reservoir, Eqs. 27 and 28 lead to Laplace’s equation for the applied electrical potential (Avants et al. 1999; Alshawabkeh 2001):

$$\begin{array}{*{20}c} {\nabla \cdot {\mathbf{E}} = - \nabla^{2} \varPhi = 0 } \\ \end{array}$$
(29)

To complete Eq. 30, appropriate boundary conditions must be prescribed.To summarize “Governing equations” section, the governing equations used in this study are the pressure equation (Eq. 22), the saturation equation (Eq. 21), and Laplace’s equation for the electrical potential (Eq. 29).

Numerical solution scheme

Inspired by the work of Arnes et al. 2007, we used a cell-centered finite volume scheme, also referred to as the two-point flux approximation (TPFA) in the literature, to discretized the saturation (Eq. 21) and pressure (Eq. 22) equations. The scheme uses the cell-averages between each cell and its neighboring cells to approximate the interfacial fluxes due to the applied pressure and electrical potential gradient (Arnes et al. 2007).

The Implicit-Pressure-Explicit-Saturation (IMPES) method is used to solve the pressure (Eq. 22) and saturation equations (Eq. 21). IMPES is a scheme used for problems with intermediate difficulty and nonlinearity (e.g., two-phase incompressible flow) (Chen et al. 2006). The main advantage of the scheme is separation of the computation of pressure from that of saturation by obtaining a single pressure equation from the combination of flow equations (Aziz and Settari 1979; Chen et al. 2004). The pressure is advanced implicitly in time, and the saturation is updated explicitly. Despite the advantages of the method, it also involves stability issues that originate from the explicit solution of the saturation equation (Aziz and Settari 1979). To overcome this issue, small time steps can be used; however, this leads to additional computational effort and may render the method inapplicable for extremely computationally challenging problems (Chen et al. 2004).

As we solve the saturation equation explicitly, it is important to ensure imposing a stability condition, called the Courant–Friedrichs–Lewy (CFL) condition, on the time step. Therefore, the solution of the saturation equation includes local time steps that ensure the stability at each global time step. Adhering to this condition ensures that the water saturation will not take values less than Swc or greater than (1 − Sor). The imposed condition in this case is (Arnes et al. 2007):

$$\begin{array}{*{20}c} {\Delta t \le \frac{{\varphi \left| {\varOmega_{i} } \right|}}{{u^{\text{in}} \hbox{max} \left\{ {f^{{\prime }} \left( s \right)} \right\}_{0.2 \le s \le 0.8} }} } \\ \end{array}$$
(30)
$$\begin{array}{*{20}c} {u^{\text{in}} = \hbox{max} \left( {q,0} \right) - \mathop \sum \limits_{j} \hbox{min} \left( u \right)_{\text{pressure}} - \mathop \sum \limits_{j} \hbox{min} \left( u \right)_{\text{voltage}} } \\ \end{array}$$
(31)
$$\begin{array}{*{20}c} {f^{{\prime }} \left( s \right) = \frac{1}{{1 - S_{\text{wc}} - S_{\text{or}} }}\frac{ f}{{\vartheta S_{\text{e}} }} } \\ \end{array}$$
(32)

where Δt is the local time step, \(\left| {\varOmega_{i} } \right|\) is the area of the finite volume cell, uin is the inflow flux of the cell, (u)pressure is the cell interface fluxes due to the pressure gradient, (u)voltage is the interface flux due to voltage gradient, and f is the fractional flow.

The local time step condition depends on the saturation only through the flux, so the new local time step is modified every time a new solution to the pressure equation is computed.

The heterogeneity of reservoirs causes upscaling issues when moving from the core scale to the reservoir scale. In particular, the values of absolute hydraulic permeability, porosity, relative hydraulic permeability, and absolute and relative electro-osmotic permeability are usually determined at the core scale, which causes problems when using these values at the reservoir scale (Ghazanfari 2013). In this study, for simplicity, we are considering a homogeneous and isotropic reservoir to limit the effects of upscaling without, however, eliminating it completely.

Simulation steps

The steps followed for the numerical simulation are:

  1. (a)

    Input of primary parameters (e.g., geometry of reservoir, geometry of cells, properties of medium, properties of fluids, injection rate, applied current density, resistivity of water, time parameters).

  2. (b)

    Input of initial saturation and calculation of initial saturation-dependent electrical properties (e.g., resistivity, voltage gradient, relative electro-osmotic permeability).

  3. (c)

    Calculation of initial saturation-dependent coefficients (pressure and voltage) for the pressure equation.

  4. (d)

    Calculation of voltage and pressure distributions (implicitly).

  5. (e)

    Calculation of flux caused by pressure and voltage gradients.

  6. (f)

    Calculation of local time step for stability.

  7. (g)

    Calculation of water saturation of the next time step (explicitly).

  8. (h)

    Calculation of saturation-dependent electrical properties of the next time step.

  9. (i)

    Calculation of saturation-dependent coefficients (pressure and voltage) for the next time step.

  10. (j)

    Repeat steps d to i until the end of the simulation period.

Numerical-experiment set-up

As mentioned in “Introduction” section, the well configuration in EEOR method is typically such that a single well is used for injection (anode) at the center of the reservoir and an array of four production wells (cathodes) are placed around the injection well on the four corners of the reservoir (Wittle and Hill 2006; Wittle et al. 2011). To facilitate the initial implementation of the equations and for simplicity, a system of one injection well and one production well placed in opposite corners of a hypothetical 2-D sandstone reservoir is used in this study. The grid consists of square cells with dimensions of 12 × 220 × 1 grid-blocks, with 26,400 cells in total. The selected parameters for the reservoir were taken from reasonable ranges available in the literature (Brooks and Corey 1964; Bassiouni 1994; Alshawabkeh 2001; Christle and Blunt 2001; Sadikh-Zadeh 2006; Wittle and Hill 2006; Arnes et al. 2007; Wittle et al. 2011; Ghazanfari et al. 2014; Chillingar and Haroun 2014; Yu et al. 2017), and are presented in Table 1.

Table 1 Characteristics of reservoir used in numerical simulation
Full size table

For the pressure equation (Eq. 22), no-flow boundary conditions around the reservoir are imposed (Aziz and Settari 1979; Chen et al. 2006; Arnes et al. 2007). Typically for field applications of the EEOR method, the current density is maintained constant and no flow of electrical current is assumed through the boundaries of the examined reservoir (Avants et al. 1999; Alshawabkeh 2001). Similar to the pressure equation, values are assigned to the electrodes to facilitate the calculation of electrical potential using Eq. 29 (Avants et al. 1999; Alshawabkeh 2001):

$$\begin{array}{*{20}c} {\left. \varPhi \right|_{\text{anode}} = \varPhi_{\hbox{max} } } \\ \end{array}$$
(33)
$$\begin{array}{*{20}c} {\left. \varPhi \right|_{\text{cathode}} = 0 } \\ \end{array}$$
(34)

where Φmax is the maximum applied voltage calculated by:

$$\begin{array}{*{20}c} {\varPhi_{\hbox{max} } = E_{\text{electrodes}} R } \\ \end{array}$$
(35)

where Eelectrodes is the applied voltage gradient between the electrodes, and R is the distance between the anode and cathode (diagonal of reservoir). The Eelectrodes is calculated every time the saturation changes using Eq. 28.

The coefficient matrix of the pressure equation that includes the total mobility of the phases (Eqs. 11 and 22) demonstrates an inherent singularity in the problem that is usually overcome by setting a constant value of pressure, thereby ensuring a unique solution (Arnes et al. 2007). In this study, the global pressure at the production well is set to a fixed value (Table 1) based on reasonable values from the literature (Christle and Blunt 2001). The total simulation period is set to 1000 days with a global time step of 1 day. Each global time step is solved as many times (local time steps) as required to maintain the stability of the solution (Eq. 30).

Figures 2 and 3 present the pressure and the voltage distribution, respectively, at various times. The pressure and the voltage appear to follow the same distribution pattern with the highest values being at the injection well, as expected. The maximum value of both pressure and voltage parameters at the injection well decreases as the waterfront propagates toward the production well, while the values further away from the injection well start to increase until they reach the proximity of the production well. As the water saturation in the reservoir increases, the resistivity of the medium decreases, and consequently, for a constant applied current density, the voltage drops (see Eq. 28).

Fig. 2
figure 2

Pressure distribution (in Pa) in the reservoir at: a 250 days, b 500 days, c 750 days, and d 1000 days (injection well at the lower left corner; production well at the upper right corner)

Full size image
Fig. 3
figure 3

Voltage distribution (in volts) in the reservoir at: a 250 days, b 500 days, c 750 days, and d 1000 days (injection well at the lower left corner; production well at the upper right corner)

Full size image

The water front appears to reach the production well at around 100 days as can be seen in Fig. 4. It appears to move faster at the middle of the reservoir until it reaches the production well (Fig. 4b, c), and then it expands toward the boundaries of the reservoir (Fig. 4d).

Fig. 4
figure 4

Water saturation distribution at: a 10 days, b 50 days, c 100 days, d 200 days, e 500 days, and f 1000 days (injection well at the lower left corner; production well at the upper right corner)

Full size image

Since adequate EEOR field data are not available in the literature to allow the calibration of the developed model, an analysis was performed to examine the model sensitivity to various parameters related to the reservoir. In order to compare the results from the analysis, the cumulative oil production (i.e., the gross amount of oil produced over a time period) is calculated under different scenarios and the results are presented in “Results and discussion” section. Then, the effects of parameters critical to the transport phenomena controlling the oil production in EEOR combined with water flooding are investigated.

Results and discussion

Sensitivity analysis

The sensitivity analysis was performed on important reservoir parameters involved in EEOR combined with water flooding including: porosity, absolute electro-osmotic permeability, relative hydraulic and electro-osmotic permeability, initial water saturation, and oil viscosity.

Porosity

The porosity (φ) is usually related to the permeability and different empirical correlations, and models have been developed to predict the permeability of the reservoir using porosity measurements (Handhal 2016). For the purpose of this analysis, the reservoir is considered to be homogeneous and isotropic with constant porosity. The range of porosity values selected for sandstone in this analysis is 0.1–0.3 (Sadikh-Zadeh 2006). As shown in Fig. 5a, the porosity value significantly affects the cumulative oil production. For instance, a 50% decrease of porosity results in about a 37% decrease in cumulative oil production at 1000 days. This was expected as the change in the reservoir porosity results in a change in the available pore space, and thus, the change in the amount of oil stored in the reservoir. In addition, the porosity affects the flow due to the applied electrical field. Equations 23 and 26 indicate that an increase in the porosity of the reservoir results in a decrease in the total resistivity. Since in the EEOR method the applied current density is usually kept constant (Wittle et al. 2011; Ghazanfari 2013), the reduction in the total resistivity will, in turn, result in an increase in the voltage gradient and subsequently an increase in the flow (i.e., oil production).

Fig. 5
figure 5

Variation of cumulative oil production with: a porosity (φ) and b relative hydraulic permeability (kr,w and kr,o) coefficients

Full size image

Relative hydraulic permeability coefficients

The relative hydraulic permeability of both phases mainly depends on the water saturation (see Eqs. 5 and 6). Another parameter involved in the estimation of the relative permeability coefficients is the pore-size distribution index, λ (Brooks and Corey 1964; Li 2004; Joekar-Niasar and Hassanizadeh 2011), with a typical range between 2 and 4 for sandstone (Brooks and Corey 1964). As shown in Fig. 5b, the cumulative oil production decreases with increase in the value of the pore distribution index, which can be explained by examining Eqs. 5 and 6. As the value of λ increases, the equations will calculate a higher value of relative permeability of water and a lower relative permeability of oil compared to the cases for lower values of λ. Therefore, the mobility of water increases and that of oil decreases, which in turn results in the oil production drop.

Absolute electro-osmotic permeability

While the absolute permeability is influenced by the pore size and pore distribution in the medium, the absolute electro-osmotic permeability is mainly dependent on the porosity (Alshawabkeh 2001). The absolute electro-osmotic permeability of soils and rocks is reported to be in the order of 10−9 m2/(V s) (Alshawabkeh 2001). For this sensitivity analysis, the value of keo was altered an order of magnitude lower and higher than the selected value of 10−9 m2/(Vs) and the results are shown in Fig. 6. Lowering keo by one order of magnitude has negligible effect on the oil production. This might be attributed to the fact that the selected electro-osmotic permeability value of 10−9 m2/(Vs) is a low value, and therefore, the application of the electrical field does not result in significant flow and the total cumulative production almost matches the production due to only water flooding. However, increasing the keo value to 10−8 m2/(V s) results in about 20% increase in the cumulative oil production, thus rendering keo an important parameter for the application of the EEOR method. The increase in the cumulative oil production is mostly due to the flow induced by the applied electrical field as the absolute electro-osmotic permeability only appears in the electrical part of the governing equations for the two-phase flow.

Fig. 6
figure 6

Variation of cumulative oil production with absolute electro-osmotic permeability (keo)

Full size image

Relative electro-osmotic permeability coefficients

The relative electro-osmotic permeability coefficients (Eq. 20) for water (ker,ww) and water–oil phase (ker,wo) are saturation-dependent parameters. The ker,ww is the relative electro-osmotic permeability of only the water phase, while ker,wo captures the “drag” of the water on the oil phase due to the applied electrical field (Ghazanfari et al. 2014). In this study, the available empirical correlations that are developed for these coefficients in sandstone reservoirs (Ghazanfari et al. 2014; Chillingar and Haroun 2014) are used. Compared to the coefficients for relative hydraulic permeability, these coefficients are much smaller, particularly ker,wo (Ghazanfari et al. 2014; Chillingar and Haroun 2014). To account for variability, the sensitivity analysis scenarios are performed by altering the values of ker,ww and ker,wo by 20 and 50% for each time step involved in the simulation.

Figure 7a, b presents the results of sensitivity analysis for ker,ww and ker,wo, respectively. The change in neither coefficient seems to significantly affect the cumulative oil production. The minor importance of these coefficients can be attributed to the fact that these coefficients will be multiplied by the absolute electro-osmotic permeability parameter, which is on the order of 10−9 m2/(V s). Hence, these changes do not significantly affect the flow outcome (Eqs. 21 and 22). It is also important to note that ker,wo, in particular, is less than 0.1 for a wide range of water saturations (Ghazanfari et al. 2014; Chillingar and Haroun 2014), which might explain the fact that a change in its magnitude has insignificant effect on flow.

Fig. 7
figure 7

Variation of cumulative oil production with a relative electro-osmotic permeability of water (ker,ww) coefficient and b relative electro-osmotic permeability of water–oil (ker,wo) coefficient

Full size image

Initial water saturation

The initial water saturation is an important parameter for the evaluation of an oil reservoir and one of the most challenging parameters to quantify (Ringen et al. 2001). The importance of the parameter is due, as seen in the governing equations presented in “Governing equations” section, to the many saturation-dependent parameters that control the flow. The water saturation not only influences the flow due to the pressure gradient but also plays a major role in the parameters controlling the flow due to the applied electrical gradient (e.g., reservoir resistivity). In addition, water saturation controls the volume of oil that is stored/available in the reservoir. Figure 8a presents the results for cumulative oil production for different initial water saturations. As expected, the higher water saturations produce less oil (i.e., 80% lower for a 50% increase in the water saturation) than the lower ones (up to 45% more oil for a 25% decrease in initial water saturation).

Fig. 8
figure 8

Variation of cumulative oil production with a initial water saturation (Sw) and b oil viscosity (μο)

Full size image

Oil viscosity

The mobility of a phase (see Eq. 4) depends on: (1) the absolute permeability of the porous media, (2) the relative hydraulic permeability of the phase (saturation-dependent), and (3) the viscosity of the phase. The effects of the first two parameters on the flow were investigated in previous sections. The viscosity of crude oil usually ranges from 0.003 to 10 kg/(ms) (Ghazanfari et al. 2014; Guo et al. 2016). In this study, we used a light crude oil with a viscosity of μο = 0.003 kg/(ms). To examine the effect of oil viscosity on flow, a wide range of viscosity values [0.003 to 2 kg/(ms)] were selected for the sensitivity analysis. As expected, the results of the analysis show that higher oil viscosity results in less oil production as shown in Fig. 8b. For example, the reservoir with lighter oil in Fig. 10 produces 98% more oil than the heaviest oil case. This significant difference in oil production indicates that a reservoir with such high-viscous oil might not be exploitable by the combination of water flooding and EEOR methods.

Effects of operational parameters on flow

The sensitivity analysis provided in the previous section showed that the developed model is sensitive to changes in the important reservoir parameters affecting oil production. To gain a better understanding of the contribution of an applied electrical field to the flow in the EEOR method, the effects of important operational parameters on oil production are investigated in this section.

Applied current density

One of the most important parameters to consider for the application of an electrical field to an oil reservoir is the applied current density. The current density not only affects the amount of extracted oil due to the applied electrical gradient (Eq. 28), but also primarily controls the cost of the EEOR method (Wittle and Hill 2006; Wittle et al. 2011). Usually, in the field, the current density is maintained constant (Wittle et al. 2011; Ghazanfari 2013). The lowest feasible applied current density is 0.1 A/m2, and the highest is no more than 5 A/m2 (Wittle and Hill 2006; Wittle et al. 2011; Chillingar and Haroun 2014). In this study, the selected value is 1 A/m2 and the range of current density for the sensitivity analysis is 0.1–5 A/m2. As can be seen in Fig. 9a, a decrease in applied current density of 90% results in about 4% less oil production. To achieve a 4 and 8% increase in the oil production, the current density should be increased by 100 and 400%, respectively. As expected, the current density is an important parameter in the EEOR method as affects the flow due to the applied electrical field.

Fig. 9
figure 9

Variation of cumulative oil production with a applied current density and b water resistivity

Full size image

Reservoir resistivity

Reservoir resistivity affects current flow, and in turn oil production (Eq. 23) due to an applied electrical field. The applied electrical gradient is proportional to the average resistivity of the reservoir (Eq. 28). Therefore, a decrease in the resistivity, while maintaining a constant current density, results in a decrease in the applied voltage gradient, and thus a decrease in the fluid flow due to applied electrical field. The resistivity of the water (and in turn the reservoir) varies with the salinity of the injected water (Bassiouni 1994; Sheng 2014).

A wide range of water resistivity values was selected to represent the variability in the salinity of the injected water. Figure 9b demonstrates simulations results for various water resistivity values. The higher resistivities appear to produce more oil than the those with the lower resistivities, thereby validating the relationship between voltage gradient and resistivity. The water resistivity appears only in the equations for the electrical part of the flow, meaning that the increase in oil recovery is mainly driven by the applied electrical field. The developed model is assuming immiscible flow, and therefore, the effects of changes in the salinity of water on the pressure-driven flow are not considered.

Injection rate

Higher water flooding rates lead to higher oil production due to an increase in the pressure difference between the injection and the production wells. Figure 10 shows a 20% increase in oil production for a 200% increase in the water flooding rate. However, it should be noted that this high injection rate might not be practical in the field. Also, it should be noted that the increase in the water flooding rate might adversely affect the electrical part of the flow (lower resistivity results in lower voltage gradient), but this effect is shadowed by the significant effect of the pressure-driven part of the oil production.

Fig. 10
figure 10

Variation of cumulative oil production with applied water flooding rate (qin)

Full size image

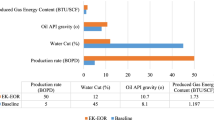
Comparing flow in two cases: only water flooding, and EEOR combined with water flooding

In order to investigate the feasibility of implementing the EEOR method for oil production, a comparison of oil production between water flooding alone and EEOR combined with water flooding was performed. All parameters for the two cases are identical except for the electrical parameters that are only present in the combination of water flooding with EEOR. Figure 11 demonstrates the results of this comparison. The combination of EEOR and water flooding appears to result in an additional 4% cumulative oil production after 1000 days. This 4% increase is attributed to the application of EEOR and is consistent with the reported values in the literature (Wittle and Hill 2006; Wittle et al. 2011; Al Shalabi et al. 2012b). If the result from the only water flooding is compared to the result from the 5 A/m2 applied current density (see Figs. 9a, 11), the oil production is 12% higher for the combination of EEOR and water flooding. However, the application of EEOR is much costlier for a current density of 5 A/m2 compared to the selected current density of 1 A/m2 (Chillingar and Haroun 2014).

Fig. 11
figure 11

Comparison of cumulative oil production for two cases: (1) only water flooding, and (2) combination of EEOR and water flooding

Full size image

Conclusions

This study numerically investigates the two-phase immiscible fluid flow involved in EEOR method. The contribution of pressure and electrical gradients to the two-phase flow were incorporated in the set of governing equations, solved using implicit-pressure-explicit-saturation technique. A numerical experiment was designed to evaluate the significance of involved parameters, and the sensitivity of the developed model to various reservoir and operational parameters was investigated. In addition, the contribution of applied electrical field to the flow was investigated. The sensitivity analysis showed that porosity, absolute electro-osmotic permeability, initial water saturation, oil viscosity, applied current density, water resistivity, and water flooding rate are critical to the transport phenomena controlling the oil production in EEOR method.

The applied electrical gradient involved in EEOR combined with water flooding was found to contribute to a very small increase in oil production. It should be noted that the reported conclusions are based on several assumptions and the authors acknowledge the limitations involved in the development and application of this numerical simulation due to scarcity of experimental and field data on the EEOR method for calibration of the model. Future work may include improvements in the model such as (1) evaluation of the effects of different well configurations (anode, cathode configurations) on oil production, (2) incorporating the effects of the applied electrical field on the oil viscosity and coefficients of relative hydraulic permeability, (3) fully coupling the pressure and electrical gradients, and (4) incorporating the non-isothermal effects due to joule heating of the reservoir.