Introduction

The deposition of hydrate, scale, wax, and asphaltene in wellbores and pipelines has been a flow assurance concern for oil and gas industry. Among these concerns, asphaltenes pose a special challenge, because asphaltenes are not well understood and can deposit even at a high temperature. Aspects like light oils to be more prone to develop problems with asphaltene than heavy oils make the problem even more challenging (Sarma 2003). New advancements in enhanced oil recovery and gas lift processes also have been encountered to reduce asphaltene instability, which induces asphaltene precipitation and deposition (Abouie et al. 2015; Fallahnejad and Kharrat 2015; Jafari Behbahani et al. 2012; Nasrabadi et al. 2016).

Asphaltene is the heaviest component of petroleum liquid. Generally accepted definition of this fraction is by solubility regime: insoluble in alkanes such as n-pentane (C5) or n-heptane (C7), but soluble in aromatic solvents such as toluene, benzene, or pyridine (Mullins et al. 2007). Since asphaltenes comprise a spectrum of individual molecules, within a solubility regime, the exact molecular compositions of many of the molecules are unknown and the material is usually characterized by bulk properties. However, the recent studies pointed that asphaltenes are like an “island” containing a polyaromatic core, and these molecules have relatively small molecular weights ranging from 500 to 100 g/mol (Adams 2014).

Generally, asphaltenes are stable in oil phase at reservoir conditions. Variation in temperature, pressure, and composition of oil can induce asphaltene instability. Asphaltene stability in crude oil has been the subject of investigations over many years (Abouie et al. 2016; Arciniegas and Babadagli 2014; Mohebbinia et al. 2014; Prakoso et al. 2016; Sedghi and Goual 2014; Tavakkoli et al. 2011, 2013). The existing models for asphaltene stability can be classified as either thermodynamic or scaling models (Behbahani et al. 2013). Thermodynamic models are based on the complex properties of asphaltene such as interaction coefficient, critical properties, acentric factor, and solubility parameter, while scaling models are based on aggregation and gelation phenomena (Rassamdana et al. 1996). Asphaltene instability is often reported as precipitation or deposition interchangeably; however, the difference is well defined. Precipitation is defined as the formation of a solid phase from the bulk liquid phase, primarily as a function of thermodynamic variables (i.e., pressure, temperature, and composition). Deposition, however, is characterized by the formation and growth of a solid layer on a surface (Juyal et al. 2013). Therefore, precipitation is a prerequisite to asphaltene deposition, but it is not a sufficient condition for deposition (Akbarzadeh et al. 2011). Much progress has been made in the area of asphaltene precipitation in the past several decades, although the mechanism of asphaltene deposition is still not well understood (Alboudwarej et al. 2004; Juyal et al. 2013).

Over the past few decades, several researchers have proposed particulate fouling and asphaltene deposition models to study the solid deposition on the pipe wall. Friedlander and Johnstone (1957) proposed that large particles (~1 µm diameter) radially transported by virtues of eddy diffusion and particle inertia. The model predictions were compared with experimental data where a fairly good agreement was obtained. Beal (1970) employed aspects of the previous model (Friedlander and Johnstone 1957) and developed a model suitable for both small and large particle depositions. The author considered that small particles would be transported by Brownian motion and eddy diffusion, as it was proposed by Lin et al. (1953), while large particles would be transported by eddy diffusion and particle inertia, as it was proposed by Friedlander and Johnstone (1957). In contrast to the previous researchers, Cleaver and Yates (1975) followed a different approach, applying probabilistic theory, to develop the particle deposition model. In their calculations, the simple mechanistic model was implemented and artificial boundary conditions were disregarded. A fairly good agreement was found after comparison of the developed model predictions (Cleaver and Yates 1975) with experimental data at the range of particle size smaller than (<1 µm).

Escobedo and Mansoori (1995) first developed asphaltene deposition model based on a previous model (Beal 1970) used for aerosol (microscopic liquid or solid particles dispersed on air currents) deposition. The model was developed by accounting for both diffusive and convective mechanisms for transport of asphaltene particle to the pipe wall (Paes et al. 2015; Zeinali Hasanvand et al. 2016).

Jamialahmadi et al. (2009) performed experiments to measure the rate of asphaltene deposition in a flow-loop apparatus. The experimental results showed that the deposition rate increases by increasing the asphaltene mass fraction and surface temperature and decreases by increasing the crude oil velocity.

Vargas et al. (2010) developed a model consisting of sub-models describing the particle precipitation, agglomeration, transport, and deposition on the wall. The aggregation and deposition stages are modeled using pseudo-first-order reactions. The particle transport is described by the convection–diffusion equation. The model contains several tuning parameters that have to be identified based on the experimental data. In the most recent work, Hashmi et al. (2015) assumed that diffusion is the main driving mechanism in asphaltene deposition on the metal surface and introduced a new deposition model. Asphaltene deposition was assessed by injecting precipitating petroleum fluid mixtures into a small metal pipe, which results in deposition and clogging. Measurement of pressure drop across the pipe was used to understand dynamics of asphaltene deposition. The agreement was found between model predictions and experimental data. However, the model was developed for laminar flow, and further investigation is required to apply the model to turbulent flow of oil from a wellbore.

Shirdel et al. (2012) studied the application of Friedlander and Johnstone (1957), Beal (1970), Cleaver and Yates (1975), and Escobedo and Mansoori (1995) models to predict the published experimental data. In the first part of their paper, they used Friedlander and Johnston’s (1957) aerosol data set. In the second part, they used Jamialahmadi et al.’s (2009) experimental data set.

In this work, the oil well in south Kuwait’s Marrat reservoir was selected to study asphaltene precipitation and deposition along the production tube. An appropriate thermodynamic model (solid model) was used to identify the asphaltene precipitation zone, and then five deposition models were applied to the wellbore and compared with reported deposit, a work similar to Shirdel et al. (2012), but in the field scale.

Deposition models

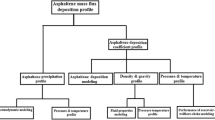
The asphaltene deposition models consist of three major modules: (1) particle transport toward the wall surface, (2) particle attachment process to the surface, and (3) particle concentration gradient between fluid bulk and the wall surface. Contribution of these modules in asphaltene deposition rate can be expressed according to the following relationship:

$$\dot{m} = K_{\text{t}} \times {\text{SP}} \times (C_{\text{b}} - C_{\text{s}} )$$
(1)

In Eq. (1), K t is the transport coefficient which considers the macroscopic and microscopic mechanisms, SP is the sticking probability, and (C b − C s) is the concentration gradient between fluid bulk and wall surface.

Transport coefficient

For accurate calculation of asphaltene deposition rate, comprehensive knowledge of effective mechanisms contributing in deposition process is necessary. In order to study this complex mass transfer problem, the asphaltene deposition was placed within a general context of particle deposition during a turbulent flow.

A parameter which is related to particle and flow characteristics is particle relaxation time. The physical meaning of the relaxation time comes from Stokes stopping distance of an immersed particle. Stokes stopping distance is defined as the distance a particle (mass, m p, diameter, d p, and density, ρ p), with an initial velocity V 0, travels in free-flight through a stagnant fluid before it stops because of drag forces. The force balance on the particle in horizontal direction results in (Friedlander and Johnstone 1957):

$$m_{\text{p}} \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} = - 6\pi \mu r_{\text{p}} \frac{{{\text{d}}x}}{{{\text{d}}t}}$$
(2)

where x is the particle position at a given time t. The particle’s velocity can be evaluated by integrating Eq. 1 with boundary condition \(\frac{{{\text{d}}x}}{{{\text{d}}t}}\left| {_{t = 0} } \right. = V_{0}\) and considering that the particle’s mass is given by \(4\pi r_{\text{p}}^{3} \rho_{\text{p}} /3\) (Paes et al. 2015):

$$\frac{{{\text{d}}x}}{{{\text{d}}t}} = V_{0} \exp ( - t/\tau_{\text{p}} )$$
(3)

The stopping distance, S p, can be evaluated by considering that x approaches S p when t tends to infinity:

$$S_{\text{p}} = \tau_{\text{p}} V_{\text{p}}$$
(4)

where t p is the particle relaxation time, defined as

$$\tau_{\text{p}} = \frac{{\rho_{\text{p}} d_{\text{p}}^{2} }}{18\mu }$$
(5)

Particle relaxation time is converted to dimensionless form as

$$\tau_{\text{p}}^{ + } = \frac{{\rho_{\text{p}} d_{\text{p}}^{2} }}{18\mu } \times \frac{{\frac{f}{2}V_{\text{avg}}^{2} }}{\nu }$$
(6)

where V avg is the average liquid velocity (m/s) and f is the fanning friction factor and can be calculated from classical Blasius equation (Prandtl 1935) for smooth tube flow:

$$f = \frac{0.3164}{{\text{Re}^{0.25} }}$$
(7)

Disregarding the electrostatic and thermophoresis effects between surface and particles, we may have three different mechanisms for particles deposition. Based on dimensionless particle relaxation time, one of the mechanisms becomes dominant (Shirdel et al. 2012). We define these mechanisms as: diffusion \((\tau_{\text{p}}^{ + } < 0.1)\), inertia \((0.1 < \tau_{\text{p}}^{ + } < 10)\), and impaction \((\tau_{\text{p}}^{ + } > 10)\) (Epstein 1997).

In the following sections, we briefly discuss the five selected models: Friedlander and Johnstone (1957), Beal (1970), Cleaver and Yates (1975), Escobedo and Mansoori (1995), and Jamialahmadi et al. (2009). The mathematical equation of each model is provided in Table 1.

Table 1 Transport coefficients for different deposition models
Full size table

Friedlander and Johnstone model

Friedlander and Johnstone (1957) applied the classical approach in order to obtain the transport coefficient (K t). In this approach, mass transfer flux was formulated by analogy to the momentum transfer in turbulent flow. The shear stress which is momentum flux is defined as:

$$\tau = (\mu + \rho \varepsilon )\frac{{{\text{d}}V}}{{{\text{d}}y}}$$
(8)

By analogy, using molecular diffusivity instead of kinematic viscosity and eddy diffusivity instead of viscosity, we obtain mass transfer flux as:

$$N = (D_{\text{m}} + \varepsilon )\frac{{{\text{d}}C}}{{{\text{d}}y}}$$
(9)

In order to calculate the total mass flux, authors used Lin et al.’s (1953) model in which flow regions are divided into three sections known as a sub-laminar layer, a buffer region, and turbulent core where the velocity and eddy viscosity distribution are correlated at each region. Friedlander and Johnstone (1957) performed integration of concentration difference for three different flow zones. The integration intervals consist of the stopping distance from the wall to the edge of the sub-laminar layer, then from the sub-laminar layer to the end of the buffer zone, and finally, from the buffer zone to the turbulent core. In addition, by considering large particles, they neglected Stokes–Einstein diffusivity (Brownian motion). Hence, Friedlander and Johnstone (1957) calculated the transport coefficient in three conditions, depending on the stopping distance value, which can be located inside the sub-laminar layer, buffer zone, or turbulent core.

Beal model

Contrary to Friedlander and Johnstone (1957), Beal (1970) developed a model suitable for both small and large particles by considering Brownian diffusion. In addition, Beal (1970) assumed a linear equation for mass and momentum flux.

Cleaver and Yates model

Cleaver and Yates (1975) applied a stochastic approach to obtain the transport coefficient. Stagnation point flow model was assumed for the motion of fluid toward the wall, and a model accounting for both upsweeps and downsweeps of the fluid in the wall region was developed.

Escobedo and Mansoori model

Escobedo and Mansoori (1995) developed a model similar to Beal’s (1970); however, they did not use the Reynolds analogy for the turbulent core diffusion.

Jamialahmadi et al.’s model

Jamialahmadi et al. (2009) proposed that the transport coefficient of the submicron asphaltene particles can be obtained from empirical correlations for forced convective heat transfer. Chilton and Colburn’s analogy was used by replacing the Nusselt and Prandtl numbers by the Sherwood and Schmidt numbers in Prandtl equation. Assuming the Schmidt number in the order of 106 and some manipulation, they further simplified the model.

As it can be noticed, the equation for the transport coefficient differs very slightly from those found by Cleaver and Yates (1975) model; however, they were developed in entirely two different approaches. Hence, in this work we will discuss the Cleaver and Yates (1975) model which can be also representative of Jamialahmadi et al.’s (2009) model.

Sticking process

Once the asphaltene particles reach the wall, a fraction of them sticks to the wall. This fraction can be defined as follows (Watkinson 1968):

$${\text{SP}} \propto \frac{{{\text{Adhesive}}\;{\text{bond}}\;{\text{between}}\;{\text{particle}}\;{\text{and}}\;{\text{surface}}}}{{{\text{Average}}\;{\text{shear}}\;{\text{stress}}\;{\text{on}}\;{\text{particle}}\;{\text{at}}\;{\text{surface}}}}$$
$${\text{SP}} = {\text{SP}}_{0} \frac{{F_{\text{adh}} }}{{F_{\text{drag}} }}$$
(10)

One can find from Eq. (10) that when SP = 1, the deposition rate is limited by transport coefficient and mass transfer controls the process. In this case, all particles arriving at the wall stick to it. The adhesion force generally obeys Arrhenius expression and can be written as (Watkinson 1968)

$$F_{\text{adhesive}} = F_{\text{a}} e^{{\frac{{ - E_{\text{a}} }}{{RT_{\text{s}} }}}}$$
(11)

where F a is a constant, E a is the activation energy, and T s is the surface temperature. On the other hand, the drag force on the particle is given by:

$$F_{\text{drag}} = A_{\text{p}} \frac{{\rho V_{\text{avg}}^{2} }}{2}C_{\text{d}}$$
(12)

Therefore, by substituting equations in sticking probability equation:

$${\text{SP}} = {\text{SP}}_{0} \frac{{2F_{\text{a}} e^{{ - \frac{{E_{\text{a}} }}{{RT_{\text{s}} }}}} }}{{C_{\text{d}} A_{\text{p}} \rho V_{\text{avg}}^{2} }}$$
(13)

which can be written as:

$${\text{SP}} = K_{\text{d}} \frac{{e^{{ - \frac{{E_{\text{a}} }}{{RT_{\text{s}} }}}} }}{{V_{\text{avg}}^{2} }}$$
(14)

where E a and K d are activation energy and frequency factor, respectively, which are related to asphaltene particle and tubing properties and calculated from experimental tests. Unfortunately, these parameters are not available for Marrat oil well. Jamialahmadi et al. (2009) conducted experiments on the deposition of asphaltene particles from Middle East oil and by curve fitting found that E a = 65.3 kJ/mol and K d = 9.76 × 108. We used the same value for E a and a reasonable value in the same for K d. Table 2 represents these values and other parameters in the deposition models.

Table 2 Parameters of sticking probability and mean diameter of asphaltene particle
Full size table

Particle concentration gradient

(C b − C s) is the concentration drop which provides the driving force between solution bulk and solid–fluid interface. C b is the average bulk particle concentration. In the system containing oil and solid phase, the average bulk particle concentration is predicted through a thermodynamic equilibrium between oil and a solid phase which will be described in the next section. C s is the surface particle concentration and is known as a lower boundary condition of particle deposition flux. This boundary is regarded as a zero particle concentration at the pipe wall at most of the practical use.

Asphaltene precipitation model

In this study, we use the solid model introduced by Gupta (1986) to predict the amount of asphaltene precipitation and Peng and Robinson (1976) equation of state to model the oil and gas behavior. We used Nghiem et al. (1993) method for characterizing the asphaltene solid phase, in which at equilibrium conditions, the fugacity of each component in all phases (e.g., solid, liquid, and gas) is the same as presented in the following equation:

$$\begin{array}{*{20}c} {f_{i,o} = f_{i,g} ,} & {i = \, 1, \ldots ,n_{c} } \\ {f_{{n_{c} ,o}} = f_{\text{asph}} } & {} \\ \end{array}$$
(15)

The fugacity of each component in the oil and gas phase is calculated from the Peng and Robinson (1976) equation of state, and the fugacity of asphaltene in the solid phase is calculated from (Nghiem et al. 1993; Nghiem and Coombe 1997):

$$\ln f_{\text{asph}} = \ln f_{\text{asph}}^{ * } + \frac{{V_{\text{asph}} (P - P^{ * } )}}{RT}$$
(16)

where \(P^{ * }\) is the onset pressure of asphaltene at temperature T and \(f_{\text{asph}}^{ * }\) is the fugacity of asphaltene in the solid phase at temperature T and pressure \(P^{ * }\).

Wellbore and fluid data

In order to compare and evaluate the performance of models in field scale, an oil wellbore with measured asphaltene deposition profile is required. Sufficient thermodynamic properties of live oil should be available for accurate fluid characterization. Hydrodynamic data of wellbore are also required for predicting pressure and temperature route along the wellbore. The only reported asphaltene deposition profile was provided by Kabir et al. (2001), in which a caliper measurement was run in Marrat oil wellbore in south Kuwait’s oil field. Operating conditions of this wellbore are reported in Table 3 (Kabir et al. 2001). A few thermodynamic data and SARA test analysis of the oil from the same field have been reported by the same authors in Kabir and Jamaluddin (2002) also are provided in Table 3.

Table 3 Operating condition of Marrat oil well and PVT characteristics of studied oil
Full size table

In addition, Table 4 summarizes the results of saturation pressure and upper and lower onset pressure of the oil at different temperatures (Jamaluddin et al. 2002; Kabir and Jamaluddin 2002). Kurup et al. (2011) have also provided a hydrodynamic and P–T relationship of this wellbore from an internal database of Chevron. With this available information, it was possible to apply the models to this wellbore.

Table 4 Saturation pressures along with upper and lower offset pressures of oil at different temperatures
Full size table

Solution procedure for predicting deposition profile

The wellbore was discretized to 50 grids of 300 ft lengths in the z-direction. Pressure and temperature were obtained in the center of each grid from P versus T relationship provided by (Kurup et al. 2011). However, in this work, pressure and temperature versus depth were required. Hence, it was assumed that pressure varies from bottomhole pressure (8400 psi) until wellhead pressure (350 psi) linearly. And then, the temperature of each grid with known pressure was obtained from available P–T relationship. The pressure profile is not entirely linear in wellbores; however, because of lack of data, at this point, this assumption was made. The obtained P–T relationship in this work was compared with field data reported in the work of Kurup et al. (2011) in Fig. 1.

Fig. 1
figure 1

Pressure and temperature of flowing fluid along the oil wellbore. **Kurup et al. (2011)

Full size image

With available pressure, temperature at each grid, and composition of the fluid, phase equilibrium calculation was done using (Peng and Robinson 1976) equation of state in order to calculate the number of phases, phase’s density, and molar volume of each phase, and suitable correlations were used to predict the PVT properties of the flowing fluid. WINPROP, a phase behavior modeling software developed by computer modeling group (CMG), was employed to predict the weight percent of the precipitated asphaltene. In MATLAB programming software, all mentioned calculations were combined in a single program code and coupled with deposition models. The flowchart of the method is shown in Fig. 2.

Fig. 2
figure 2

Computational procedure for prediction of asphaltene profile along the wellbore

Full size image

Results and discussion

Thermodynamic characterization and modeling of asphaltene precipitation

WINPROP was employed to perform the equilibrium flash calculation and also the construction of the solid model for modeling the asphaltene precipitation. To do the first, a common regression was run to tune the cubic EOS to PVT experimental data. Bubble point pressure at reservoir temperature (241 °F) and gas–oil ratio (GOR) were taken into account as important parameters in the tuning process. As illustrated in Fig. 3, the thermodynamic model prediction of saturation pressures for different temperatures (the dark blue line) matches very well with experimental data. For modeling the asphaltene precipitation, the heaviest plus fraction was split into a non-precipitating fraction C22A+ and a precipitating fraction C22B+. Asphaltene component parameters including solid molar volume (Vasph), and binary interaction coefficients (δ) between C22B+ and the light components up to and including C5 should be adjusted to match with the experimental data. An experimental data set of asphaltene onset pressures were taken as reference pressure P* in the solid-phase model at each isotherm. The asphaltene precipitation envelope (APE) was determined by performing flashes at varying pressures for a number of temperatures. Flash calculations using a small pressure step are used to locate the precipitation onset pressures and asphaltene offset pressures. These calculated onset and offset pressures were taken together to define the asphaltene precipitation envelope. The orange line in Fig. 3 represents the asphaltene onset pressure curve constructed from this method, where the green line represents the prediction of asphaltene offset pressures.

Fig. 3
figure 3

P–T diagram of oil/asphaltene system at different pressures and temperatures

Full size image

Figure 4 shows the comparison of the well-matched model predictions with the experimental test results. The model predictions were found after several isothermal runs at 120 and 241 °F. When the model predictions matched well with the experimental data, the values of V asph and δ were found to be 0.456 and 0.17 l/mol, respectively. As it can be seen for 241 °F, the asphaltene starts to precipitate at the pressure of 7000 psi and reaches its maximum point of precipitation at the pressure of around 3000 psi. This observation is in agreement with the fact that normally the asphaltene precipitation reaches the maximum at bubble point pressure which is also around 3000 psi as shown in Fig. 3 for 241 °F. This matched model was used for prediction of weight percent of precipitated asphaltene from crude oil at any other temperature and pressure.

Fig. 4
figure 4

Comparison of thermodynamic model predictions and reported experimental data for weight percent of precipitated asphaltene at T = 241 °F and T = 120 °F

Full size image

Fluid and flow characteristics along the wellbore

During the oil and gas production from the reservoir to the surface facility, fluid flows along a path which has a wide range of pressure and temperature variations. In fact, changes in the thermodynamic conditions influence the fluid and flow properties along the wellbore. Variations of oil formation volume factor and gas formation volume factor are shown in Fig. 5. The figure shows that at depth around 5000 ft, B o starts to decrease until it reaches 1.07 SCF/STB at the wellhead. In addition, zero values for gas formation factor below ~5000 ft show that the production fluid is undersaturated from bottomhole to the depth of ~5000 ft.

Fig. 5
figure 5

Variations in oil and gas formation volume factors along the wellbore

Full size image

As shown in Fig. 6, the evolution of gas bubbles from production fluid causes an increase in gas superficial velocity and decrease in oil superficial velocity. Oil superficial velocity starts at a rate of 11. 58 ft/s at the bottom of the wellbore and increases slowly due to decreasing liquid density until the depth around 5000 ft when it reaches 11.64 ft/s. In addition, the gas superficial velocity reaches 10.65 ft/s at the top of the wellbore, where the gas phase consists of most portion of production fluid.

Fig. 6
figure 6

Oil and gas superficial velocity profiles along the wellbore during oil production

Full size image

Asphaltene precipitation

Changes in pressure and temperature of the fluid throughout the well column are also influential in the thermodynamic conditions of the fluid. Depending on design and operational conditions of the well column, a part or all of the asphaltene precipitation boundaries may be crossed out as fluid flows upward. The identifying unstable region of asphaltene along the well is a prerequisite for prediction of the deposition profile. This precipitation region can be represented by the intersection of P–T relationship with asphaltene upper and lower boundaries. As shown in Fig. 7a, until the point of pressure 7177 psi and temperature 214.7 °F in which the fluid is at reservoir conditions, the fluid is at the single phase and asphaltene is stable in oil, which represents the stable region (1). As the well P–T relationship intersects upper asphaltene boundary at (7177 psi, 214 °F), the thermodynamic equilibrium of oil/asphaltene was disturbed and the asphaltene starts to precipitate and the unstable region (2) begins. Then, as pressure and temperature decrease continuously, more asphaltene precipitates. After that, when the well P–T relationship intersects bubble pressure curve, the gas comes out of the oil/asphaltene mixture. At this point, the system consists of three phases, namely liquid oil, solid asphaltene, and released gas. Releasing the light components at bubble point, which are normally precipitating agent of asphaltene, makes the oil a better solvent for asphaltene, and hence, the asphaltene starts to become more stable in oil until the intersection of P–T relationship with a lower boundary condition at (1650 psi, 139.5 °F). Finally, in the region (3), the asphaltene becomes completely stable in liquid oil and system becomes a single liquid phase.

Fig. 7
figure 7

a Intersection of P–T relationship with upper and lower boundaries of the asphaltene precipitation envelope. b Schematic diagram of the asphaltene precipitation zone

Full size image

This procedure can be used as a graphical method to map out the precipitation zone in Marrat oil well which is shown in Fig. 7b. The oil starts to precipitate at 7177 psi and 241 °F along its P–T relationship. The corresponding depth for this pressure is around 1270 ft in the 15,000 ft length well. Asphaltene precipitation continues until the pressure of 1650 psi, at the depth of 2500 ft, after which asphaltene precipitation ceases.

The method enabled us to identify the precipitation zone along the wellbore. The next step is quantifying the asphaltene precipitation tendency in the precipitation zone. The thermodynamic modeling of the oil/asphaltene system in the first section was used to predict the weight percent of the oil phase which precipitated. Figure 8 shows this quantity along the production tubing. The weight percent of the precipitated asphaltene is converted to asphaltene concentration by multiplying it by the live oil density to use as the asphaltene particle concentration in Eq. 1.

Fig. 8
figure 8

Profiles of weight percent of precipitated asphaltene and asphaltene concentration along the wellbore

Full size image

Asphaltene transport coefficients and sticking probability

Although the quantity of precipitated asphaltene is crucial, it is equally important to predict the transport of these precipitated particles toward the tubing wall. This process was described early in the modeling approach as the transport coefficient, representing the rate of transportation. In Fig. 9, we investigate this parameter for the four models along Marrat oil wellbore. As can be seen in all models, starting from wellbore shoe at 15,000 ft, the transport coefficient starts to increase smoothly until the depth of around 5000 ft.

Fig. 9
figure 9

Comparison of four models in predicting the asphaltene transport coefficient (K t)

Full size image

The four models have been obtained in an entirely different manner; however, their uniform increase until a specific depth is the point of interest. To analyze this behavior, we consider the simplest models Cleaver and Yates (1975) or Jamialahmadi et al. (2009) which are comprised of just three parameters (f, V l, and Sc). The trend of these parameters along the wellbore can be helpful to understand the above behavior. This analysis will also lend light for understanding the other model’s trend. Figure 10a shows variations in the fanning factor (f) and the liquid velocity (V l) along the wellbore which are proportional to the transport coefficient. Figure 10b shows variation in Schmidt number (Sc) which is inversely proportional to K t.

Fig. 10
figure 10

a Change in the liquid-phase velocity and fanning factor, b change in Schmidt number along the wellbore

Full size image

Figure 10a shows that the fanning factor (f) continuously decreases along the production tube until the depth of ~5000 ft and cannot contribute to the increase in the transport coefficient. Liquid velocity starts to increase as oil expands during liquid-phase oil production; however, this increase continues until wellhead facility and cannot be regarded to describe the increase in transport coefficient until depth around 5000 ft. The last parameter shows a trend which is the key to our understanding. As shown in Fig. 10b, Schmidt number decreases as oil move toward the depth around 5000 ft. In fact, during oil expansion along the wellbore, diffusivity coefficient (D B) increases due to decreasing oil viscosity which is inversely proportional to diffusivity coefficient. This observation suggests that asphaltene deposition in production tubing is a diffusion-driven process which supports our earlier understanding about this phenomenon (Hashmi et al. 2015).

Asphaltene deposition profile

The multistep process including asphaltene precipitation, asphaltene transportation, and attachment of asphaltene particle to the metal surface is required to form deposit layer. The first two steps were analyzed in previous sections, and they were quantified along the wellbore from bottomhole to the wellhead in Figs. 8 and 9. Figure 11 represents a change in the fraction of asphaltenes that attach to the tube’s inner wall surface when they transported toward the wall. Recalling \({\text{SP}} \propto \frac{1}{{V^{2} }}\), as fluid flows upward, oil expands and liquid velocity increases, and thus the adherency of asphaltene particles to the metal surface decreases.

Fig. 11
figure 11

Change in sticking probability (SP) in the wellbore

Full size image

Figure 12 shows the comparison of four model predictions with real measurement of asphaltene thickness from caliper along the Marrat oil well. Although the caliper measurements reported in the work of Kabir and Jamaluddin (2002) show the whole range of deposited asphaltene thickness along the depth, in this work mean value of reported measurements from the caliper was used to make the comparison more illustrative. The black line in Fig. 12 represents the mean value of reported deposit profile of Marrat oil wellbore along the production string. Unfortunately, the caliper measurement was not run from depth around 15,000 ft in order to clearly find where asphaltene deposition starts to build. As we discussed in section “Asphaltene precipitation,” all models show that asphaltene appears somewhat around the depth of 12,500 ft. This depth is in close agreement with that of Kurup et al. (2011) where they studied this wellbore with (ADEPT) deposition simulator and concluded that the deposition starts at 12,000 ft. In addition, as we can see, Cleaver and Yates (1975) model predicts asphaltene deposition profile more closely to the mean value of caliper measurement. At the maximum deposition zone, this model predicts 0.47 in. asphaltene deposit layer after 2 months of oil production. Schematic of asphaltene deposition profile formed with Cleaver and Yates (1975) and Escobedo and Mansoori (1995) models reveals that although they are completely different in the way developed, their predictions are similar to each other. This finding was also observed in the work of Shirdel et al. (2012) where these models were compared in laboratory scale.

Fig. 12
figure 12

Solid lines Asphaltene deposition profiles predicted by the four models along the axial length of Marrat oil wellbore. Black Solid Line Reported caliper measurement of the wellbore

Full size image

Figure 13 shows a comparison of the model predictions with caliper measurements at 2550, 2950, 3500, and 4000 Reynolds numbers. The corresponding depths for these Reynolds numbers are 3150, 3750, 10,000, and 5850 ft. The bar graph in this figure clearly shows difference and similarity of model predictions with each other. Also, since in the last three Reynolds numbers, caliper measurements were available, we can notice that Friedlander and Johnstone (1957) model highly underestimate the thickness of deposited layer, while the Escobedo and Mansoori (1995) and Cleaver and Yates (1975) models predict the rate of asphaltene deposition higher than Beal (1970) model.

Fig. 13
figure 13

Comparison of the model predictions with mean reported asphaltene thickness at four Reynolds numbers a 2500 (depth ~3150 ft), b 2950 (depth ~3750 ft), c 3500 (depth ~10,000 ft), d 4000 (depth ~5850 ft)

Full size image

Conclusion

In this work, five asphaltene particle deposition models were selected from the literature and were applied to the oil wellbore with measured deposition thickness. The deposition models were explained with particular attention to the assumptions and the way these models developed. To apply the models to the oil field wellbore, all available data about a Kuwait oil well were gathered for thermodynamic modeling of reservoir fluid and calculating the hydrodynamic conditions of the fluid along the wellbore. By employing the phase behavior of oil/asphaltene system, a graphical method was proposed for predicting the asphaltene precipitation zone along the wellbore. By applying the models to the studied oil well, we found that due to the small size of the asphaltene particles, the diffusion mechanism is dominant in the radial transport of the asphaltene particles toward the wall in Marrat oil well. After predicting the asphaltene transport coefficient, the concentration of precipitated asphaltene, and sticking probability along the oil well, comparison of the models with each other showed that Cleaver and Yates (1975) and Escobedo and Mansoori (1995) models approximately predict the asphaltene deposition in the same order. Comparison of the deposition models with measured caliper profile showed that Escobedo and Mansoori (1995) and Cleaver and Yates (1975) models perform well in predicting the deposition profile than other models, while Friedlander and Johnstone (1957) model had a very poor performance in this comparison. However, it should be noted that our conclusion on predictive capabilities of the models is valid just for studied oil well and generalization of findings to another well with different fluid characteristics and operation conditions must be avoided.

This paper contributed to a better understanding of asphaltene deposition process along production tubing during the reservoir natural depletion. However, there is still much to be investigated about this complex process. Systematic experimental work to understand the asphaltene adhesion/reentrainment (known as sticking probability) should be addressed in the future to make the selected models more complete and accurate to predict the asphaltene deposition profile.