Introduction

In 1978, the U.S. government defined reservoirs with a permeability of less than 0.1 mD as “tight reservoirs”. However, several studies since have shown that permeability is not, in fact, the only aspect that can identify tight gas reservoirs (Shanley et al. 2004; Aguilera and Harding 2008). Several researches characterized tight gas reservoirs by high capillary entry pressures, high irreducible water saturations, low to moderate porosity, and low permeability (e.g., Thomas and Ward 1972; Dutton 1993; Byrnes 1997, 2003). Soeder and Randolph (1987) classified low permeability reservoirs based on pore geometry into three categories: grain supported pores, slot and solution pores, and matrix-supported grains. The study emphasized that the most common pore structure of tight gas reservoirs consists of secondary solution pores connected to each other through narrow tortuous slots (or fractures) known as a dual porosity model. These slots have an important effect on permeability, as well as on gas flow through tight porous media, but they may not have significant contribution to porosity (Soeder and Randolph 1987; Aguilera 2008; Byrnes et al. 2009). Thus, the pore topology/structure of unconventional reservoirs is not only heterogeneous but also unlike conventional reservoirs. It has been found in coal, shale and tight gas reservoirs that the liquid permeability is lower than measured gas permeability (Bloomfield and Williams 1995; Byrnes 1997; Cui et al. 2009; Cluff and Byrnes 2010; Ziarani and Aguilera 2012; Ghanizadeh et al. 2014). Throat radius is the accounted parameter for this variation (Bloomfield and Williams 1995; Mehmani and Prodanovic 2014). The Knudsen number (K n) is being used as a dimensionless correction factor to quantify the amount different gas flow regimes (slip flow, transition and free molecular) as a function of pore–throat radius (Javadpour et al. 2007).

Laboratory measurements for tight porous media are costly and time-consuming. Also, studying the effect of a certain parameter in such complex pore structures is difficult due to the complexity associated with the experimental setup. As an alternative approach, pore network modeling can be used to construct physically sound models of a real porous media. Pore network modeling gives a reasonable prediction of fluid flow properties at pore scale, and offers the flexibility of studying macroscopic properties relationship with pore structure and geometries.

In pore network modeling, the complex pore structure in a rock is represented by a network of pore bodies (void spaces) and pore–throats (narrow paths that connect pore bodies) with simplified geometries. When this is successfully established, then single and multiphase flow calculations can be performed (Okabe and Blunt 2005). Detailed physics and productive capabilities for pore-scale modeling of multiphase flow at the pore scale have been reviewed in several studies (Blunt 2001; Blunt et al. 2002). At the early stages of network modeling, Fatt (1956) predicted capillary pressure and relative permeability curves of drainage using two-dimensional (2D) regular lattice networks where the radii were randomly assigned. Later, Chatzis and Dullien (1977) reviewed Fatt’s network model work and they illustrated that 3D pore network models represent the real porous media more realistically than 2D pore network models. Following this early work, extensive studies on the importance of topology, pore bodies and throats size distribution and their spatial correlations were performed (e.g., Chatzis and Dullien 1977; Jerauld and Salter 1990; Grattoni and Dawe 1994). However, most of these studies were based on regular lattice networks which are limited in reflecting the real topology and geometry of a rock. The capabilities of network modeling were enormously improved and have been applied to make many successful predictions of single and multiphase flow and transport properties including two- and three-phase relative permeability and capillary pressure of conventional formations (Ören et al. 1998; Patzek 2001; Ören and Bakke 2002, 2003; Valvatne and Blunt 2003; Piri and Blunt 2005a, b). In complex sandstones, it is recommended to create first a 3D image-based representation of the pore space that should capture the statistics of the real rock. This can be generated using a direct imaging technique such as micro-CT scanning (Okabe and Blunt 2005), or by various process/object-based modeling approaches (Bakke and Ören 1997; Ören et al. 1998; Ören and Bakke 2002, 2003). Subsequently, using various image-based network extraction techniques (Al-Kharusi and Blunt 2007; Dong and Blunt 2009), an equivalent pore network is then extracted from the 3D image to estimate the single and multiphase fluid flow properties.

Permeability and formation factor are physical properties of the rock. Permeability is defined by Darcy’s law and formation factor is defined by Archie’s law. Permeability plays a critical role in determining the potential of hydrocarbon flow in a porous medium. Further, formation factor gives an indication of the availability of pathways for transport. Both properties are sensitive to pore and throat size, connectivity and geometries. The goal of this paper is to construct physically realistic 3D pore networks of tight porous media for a better understanding the effect of pore structure and topology on formation factor–permeability and permeability–porosity relationships. These relationships are derived by combining modeled data of constructed tight media obtained based on Berea sand network properties and equivalent tight networks constructed based on mercury injection porosimetry, which quantifies throat size information. The modeled data are cross checked with published experimental data obtained by Byrnes et al. (2009) for Mesaverde tight gas sandstones. Two random network construction approaches are used. Further, the study demonstrates the validity of constructing physically tight media based on Berea sand network properties having lognormal skewed distributions obtained using the Weibull equation. Experimentally, the throat size distribution of tight gas samples is been recognized by a bimodal distribution whereas the Weibull produces a lognormal skewed distribution (Sivila et al. 2011). The importance to account for slippage, transition and diffusion effect in modeling permeability through tight porous media is inferred. A detailed data analysis is presented in the following sections.

Random network generation approaches

Two approaches are implemented to construct physically realistic 3D pore network of tight porous media. An experimental data set of Berea sandstone and tight gas sandstones obtained by Oak (1990) and Byrnes et al. (2009), respectively, are used to validate the construction procedures. Imperial College’s stochastic random network generation software developed by Idowu (2009) is used as a starting point in this research. The software requires the knowledge of network element properties of pores and throats (radius, length, volume, shape factor and connectivity) which can be obtained using image-based network extraction techniques. The primary advantage of his approach is that it can be used to generate an arbitrarily sized network. However, extracting geometrically equivalent network properties based on representative high resolution images for complex pore structure is computationally very expensive (Idowu 2009; Mehmani et al. 2013). Consequently, a Weilbull truncated equation is used instead to estimate the distribution of network elements properties (pore/throat radius, aspect ratio, length, shape factor and coordination number). The Weibull truncated equation is:

$$x = \left( {x_{\hbox{max} } - x_{\hbox{min} } } \right)\left( { - \delta \ln \left[ {R\left( {1 - e^{ - 1/\delta } } \right) + e^{ - 1/\delta } } \right]} \right)^{1/\gamma } +\,\, x_{\hbox{min} }$$
(1)

where x is the estimated property value, x min and x max are the minimum and maximum values of x property, and \(\delta\,\, {\text{and}}\,\, \gamma\) are Weibull exponent parameters. Furthermore, the area, volume and clay volume of each network element are calculated following the same formulas as Valvatne (2004):

$$A = \frac{{r^{2} }}{4*G}$$
(2)
$$V = A \times L$$
(3)
$${\text{ClayVol}} = \frac{{V \times {\text{Clayper}}}}{{\left( {1 - {\text{Clayper}}} \right)}}$$
(4)

where A is the area, r is the radius, G is the dimensionless parameter and its value depends on selected pore and throat geometries, L is the length of pore or throat, ClayVol is the estimated clay volume for each element and Clayper is the clay proportion which is an input to the program. In terms of network connectivity, pores are connected to each other in a similar procedure as Idowu (2009). Maximum length condition and correlation function between two connected pores are utilized. Briefly, each approach used in this study is summarized in the following sub-sections.

Berea sand pore and throat size distribution

The first approach required an information of pore and throat size distribution which are calculated using the Weibull equation. This approach is validated by generating an equivalent network of Berea sandstone. The estimated porosity, absolute permeability and formation factor are in good agreement with reported values of Berea sand by Al-Dhahli et al. (2012) as shown in Table 1. Further, the estimated relative permeability curves for primary drainage and imbibition are in good agreement with experiment ones (Oak 1990) as shown in Fig. 2. The input data parameters used to generate the equivalent pore network of Berea sand are based on extracted network pore and throat properties reported by Idowu (2009). The minimum and maximum values of the Weibull equation are read directly from the extracted pore and throat size distribution and the Weibull exponent parameters (\(\delta\;{\text{and}}\;\gamma\)) are assumed until a match between extracted and estimated pore and throat size distributions is achieved. Subsequently, a number of tight networks are constructed by reducing pore radius, throat radius and coordination number (connectivity) of the Berea sand network. The networks are generated by varying only the values of the Weibull exponent parameters (\(\delta )\) for pore and throat radius and coordination number without manipulating their original Berea sand network minimum, maximum and (γ) values. Figure 1 is showing the original and reduced distributions of pore and throat radius and coordination number.

Table 1 Estimated network parameters of Berea sand
Full size table
Fig. 1
figure 1

The reduced distributions of tested factors plotted with the reference distributions used for generating a 3D network of Berea sandstone

Full size image

Table 2 illustrates the estimated values of porosity, absolute permeability, formation factor obtained by pore-scale modeling software, and cementation exponent estimated by Archie’s equation assuming a = 1.0. The construction assumptions and procedures are:

Table 2 Porosity, absolute permeability, formation factor and cementation exponent values as pore and throat radius distributions changed
Full size table

  • First, re-generate Berea sand network but assuming no clay content and the pore length is pore radius × 2.0. The network is referred to as the reference network as shown in Table 2.

  • Then, the distributions of pore radius, throat radius and coordination number are reduced as shown in Fig. 1. The reduction was based on changing the Weibull coefficient delta (\((\delta )\) only where minimum, maximum and Weibull coefficient gamma (γ) values are kept constant.

  • Only the distributions of pore and throat radius are reduced together by reducing the value of Weibull coefficient (\((\delta )\). Coordination number is constant for all constructed tight networks.

  • Finally, no clay content in all constructed networks is assumed.

The objective is to examine pore network capability to replicate the macroscopic properties relationships obtained experimentally by Byrnes et al. (2009) for Mesaverde tight gas sandstones using Berea sand network properties.

Laboratory throat size distribution: case study

The laboratory measurements of Mesaverde tight gas sandstones are used as a reference to validate the second construction approach. The Mesaverde database of experimental measurements is missing the information of pore size distribution for the tested core samples. Only throat radius distribution is reported from mercury injection capillary pressure analysis. With that in mind, a second approach was developed that read the experimental cumulative distribution of throat radii and generated a best fit to the original shape of throat radius distribution. Then, the Weibull equation was used to obtain a distribution of aspect ratio according to the assumed values of Weibull equation parameters that produce good agreement with experiment porosity, permeability and formation factor. Once connectivity between pores is established, the radius of each connected pore is calculated using this formula (Valvatne 2004):

$$r_{\text{p}} = \hbox{max} \left[ {\alpha \frac{{\mathop \sum \nolimits_{i = 1}^{{n_{\text{c}} }} r_{{{\text{t}}i}} }}{{n_{\text{c}} }}, \hbox{max} \left( {r_{{{\text{t}}i}} } \right)} \right]$$
(5)

Where r p is the inscribed radius of pores, α is the aspect ratio, n c is the number of connecting throats for a pore, r ti is the radius of throat i. From this equation, the pore radius must be larger than the largest connecting throat radius. We assumed no clay content in the constructed physically realistic pore networks.

Pore-scale modeling

In this research, the Imperial College program called Pore-Scale Modeling (Valvatne 2004) is used to estimate single liquid flow properties through constructed tight porous media. The program is a quasi-static simulator of two-phase capillary dominated flow following the work of Ören et al. (1998) and Patzek (2001). They used an empirical expression derived from solutions of the Stoke’s equation for flow in pores for different geometries and for different fluid configurations. The software simulates primary drainage, wettability alteration and any subsequent cycles of waterflooding and secondary drainage. Further, software is using the dimensionless shape factor (G), as suggested by Mason and Morrow (1991) to correct for wetting layer, conductivity, and calculate capillary entry pressure as a direct function of the pore shape using expressions derived by several authors (Mason and Morrow 1991; Ören et al. 1998; Patzek 2001; Valvatne 2004). It is a ratio of cross-sectional area to the perimeter length (G = A/P 2). Further details including equations used can be found elsewhere (Valvatne 2004).

Mesaverde tight sandstone case study

Byrnes et al. (2009) conducted laboratory measurements on hundreds of samples from Mesaverde tight gas sandstones of seven major basins in the United States: Green River, Piceance, Powder River, Sand Wash, Uinta, Washakie, and Wind River. Mesaverde tight gas sandstones represent the principal gas productive basins in Western U.S. The principle study objectives were to conduct basic properties analysis (routine and in situ porosity, permeability and grain density) for all samples and then perform confined/unconfined mercury intrusion capillary pressure (MICP) and electrical properties at different brine salinities measurements on selected samples. Figure 1: The reduced distributions of tested factors plotted with the reference distributions used for generating a 3D network of Berea sandstone.

Figure 2: Comparison of measured and estimated two phase relative permeability curves in Berea sandstone, (a) primary drainage displacement, (b) imbibition displacement.

Fig. 2
figure 2

Comparison of measured and estimated two phase relative permeability curves in Berea sandstone, a primary drainage displacement, b imbibition displacement

Full size image

Figure 3 shows routine gas permeability vs. routine porosity of all tested core samples for seven Mesaverde tight gas basins. The complete experimental measurements along with final technical report can be found online at study’s website (http://www.kgs.ku.edu/mesaverde/).

Fig. 3
figure 3

Cross-plot of routine air permeability vs. routine porosity for all core samples by basin

Full size image

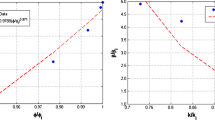
In this research, a random selection of 17 samples from three basins of Mesaverde tight gas sandstones (10 core samples from Uinta, 5 core samples from Powder River and 2 core samples from Piceane basin) are chosen. All these samples have basic properties measurements, pore–throat size distribution obtained from mercury intrusion capillary pressure (MICP) analysis and electrical properties measured at 200 K ppm brine salinity. Table 3 illustrates the basic measurements and electrical properties for each selected core sample and the ratio between estimated absolute liquid permeability by network modeling and measured routine gas permeability. Physically equivalent 3D pore networks are constructed for each core sample. Pore-Scale Modeling software was used to estimate porosity, absolute permeability to liquid and formation factor. The estimated porosity and formation factor values of modeled networks are in good agreement with reported laboratory measurements. Figure 4a, b shows the agreement between estimated and measured porosity and formation factor. However, the estimated absolute liquid permeability is lower than measured routine gas permeability for core samples having very low measured porosity and gas permeability. In core samples with higher porosity and permeability, the estimated absolute permeability to liquid is matching well the reported measured routine gas permeability. Figure 4c shows the variation in permeability values between estimated and measured data. This discrepancy has been observed by several researchers emphasizing the important to apply Knudsen’s (Knudsen 1909) or Klinkenberg’ s (Klinkenberg 1941) correction to account for slippage and diffusion effect in gas flow. This finding will be discussed in more detail in the following section.

Table 3 Experimental measurements of basic porosities and electrical properties for selected 17 core samples from three basins
Full size table
Fig. 4
figure 4

Cross-plots illustrate the agreement and deviation between experiment and estimated petrophysical properties of physically equivalent pore networks, a porosity, b formation factor, and c permeability cross-plot

Full size image

Results and discussion

For simplicity, the constructed networks based on Berea sand network properties are called tight media. Networks were constructed according to laboratory measurements are referred as equivalent networks. Figures 5, 6 show the estimated data points of formation factor vs. permeability and permeability vs. porosity, respectively, for tight media and equivalent networks plotted with experimental measurements obtained by Byrnes et al. (2009) of Mesaverde tight gas sandstones. Looking at these graphs, qualitative agreement can be seen between modeled data points of tight media and experimental data. Tight media points of formation factor vs. permeability (Fig. 5) show an inverse relationship. The experimental data clearly show this type of relationship exists, but there is scatter. This implies multitude of pore types. The model data show a similar trend as experiment data, but they all fall more or less on the same line. The presented modeled data points of tight media are generated by altering the pore and throat size distribution of Berea sand network having constant coordination number. The alteration is basically by changing the value of Weibull exponent coefficient (δ) only assuming minimum and maximum values of pore and throat radius constant. Also, another reason for the discrepancy could be that the throat length distribution is constant in all tight media networks similar to the original Berea sand network. Therefore, it can be concluded that pore and throat sizes are not the only factors that influence formation factor–permeability relationship. Throat length (tortuosity) has a significant effect on estimating the formation factor practically in tight porous media. Looking at Table 2, estimated value of formation factor is increasing dramatically from 11.1 to 3767.3 for Ref. Network and Network no. 11, respectively, by only reducing pore and throat radius having constant throat length distribution. This could be the reason that justifies the difference in slope in which experimental data show a higher order of the root (3–4). Further, looking at permeability–porosity graph (Fig. 6), the modeled data of Tight media follow the same trends as experiment data, but again the shift is by about two orders of magnitude and the slope is not the same. The big difference between the two data sets, a higher throat size distribution is used compared to the experimental data. The minimum and maximum values of estimated throat size distributions for the modeled data are 0.903 and 56.8 μm, respectively. However, the throat radius distributions of the laboratory data are much smaller. For example, an ambient mercury capillary pressure experiment was conducted on core sample Uinta@7311.9’ and the obtained throat size distribution is between 0.01 and 1.95 μm (Byrnes et al. 2009).

Fig. 5
figure 5

Formation factor–permeability cross-plot is showing the laboratory data points for Mesaverde tight gas sandstones plotted with modeled data points (formation factor-absolute permeability) for constructed tight media

Full size image
Fig. 6
figure 6

Permeability–porosity cross-plot is showing the laboratory data points for Mesaverde tight gas sandstones plotted with modeled data points (formation factor–absolute permeability) for constructed tight media

Full size image

Consequently, using representative experimental throat size distributions overcomes this issue as shown in Figs. 5 and 6. The data points of the equivalent networks follow the experimental data closely. Further, the pore and throat structure and topology of each network are different, so an accurate representation to the experiment data is achieved. However, at low permeability estimated absolute permeability differs from the experimental data as shown in Fig. 4c. The estimated absolute liquid permeability using Pore-Scale Modeling software is smaller than measured routine gas permeability. This discrepancy has been observed by several researchers emphasizing the importance to apply Knudsen’s or Klinkenberg’s correction to account for slippage and diffusion effect in gas flow (Bloomfield and Williams 1995; Byrnes 1997; Cui et al. 2009; Cluff and Byrnes 2010; Ziarani and Aguilera 2012; Ghanizadeh et al. 2014; Mehmani and Prodanovic 2014). As gas flows through very narrow throats of unconventional formations, the conventional fluid dynamic equation (Darcy’s equation) cannot be used to estimate gas permeability. Bloomfield and Williams (1995) experimentally observed this variation on sandstone and shale core samples. They found that the ratio between intrinsic or liquid permeability to gas permeability in the range of 0.03–0.9, and researchers emphasized the importance to account for slippage correction on such porous media. Ziarani and Aguilera (2012) developed a generalized typecurve for permeability correction factor in tight porous media using experiment data of Mesaverde tight gas formations, and they concluded that Knudsen’s model is more accurate than Klinkenberg’s correction model especially in very low tight reservoirs where the transition and free molecular flow regimes occur. However, their typecurve was developed based on pore–throat size that is calculated using Heid et al. (1950) which is inaccurate representation to a real tight porous media. According to their finding, Knudsen’s correction factors become more important when absolute permeability smaller than 0.1 mD. As shown in Fig. 4c, the modeled data follow this cutoff. Good agreement with experiment data is achieved above 0.1 mD, but modeled data start to deviate from experiment data for samples with permeability smaller than 0.1 mD. Mehmani and Prodanovic (2014) observed that for tube radii less than 100 nm, the diffusion and gas slip wall boundary condition should be reflected. In summary, throat size is the key parameter causing the variation between absolute permeability to liquid and gas permeability. Pore-Scale Modeling software should be extended by adding the Knudsen’s correction to model gas flow properties through tight porous media taking into account various regimes as a function of throat sizes.

Conclusions

Two approaches are used to construct physically realistic random networks of tight porous media and demonstrate the relationships of formation factor–permeability and permeability–porosity in tight porous media. Each approach is designed according to data availability.

The study demonstrates that the generated networks based on Berea sand properties show only qualitative agreement between modeled data points and experimental data, even though network properties characterized by a lognormal skewed distributions are obtained using the Weibull equation. Pore and throat sizes are not the only factors that determine the pore space of a tight porous media. It is a combination of several additional factors such as connectivity, throat length and pore/throat geometries.

A set of equivalent pore networks is constructed to represent 17 core samples from three basins of Mesaverde tight gas sandstones in U.S. Throat size distributions obtained experimentally from MICP analysis are used for constructing the equivalent pore networks. The estimated porosity, absolute liquid permeability and formation factor are in good agreement with measured data obtained by Byrnes et al. (2009). However, a variation between estimated absolute permeability to liquid and measured routine gas permeability is accounted in core samples having measured permeability smaller than 0.1 mD. The reason is that Pore-Scale software does not account for different gas flow regimes correction for very narrow throats.