An in-depth comparative analysis of data-driven and classic regression models for scour depth prediction around cylindrical bridge piers

Abstract

The study focuses on the critical concern of designing secure and resilient bridge piers, especially regarding scour phenomena. Traditional equations for estimating scour depth are limited, often leading to inaccuracies. To address these shortcomings, modern data-driven models (DDMs) have emerged. This research conducts a comprehensive comparison involving DDMs, including support vector machine (SVM), gene expression programming (GEP), multilayer perceptron (MLP), gradient boosting trees (GBT) and multivariate adaptive regression spline (MARS) models, against two regression equations for predicting scour depth around cylindrical bridge piers. Evaluation employs statistical indices, such as root-mean-square error (RMSE), coefficient of determination (R²), mean average error (MAE) and normalized discrepancy ratio (S_(DDRmax)), to assess their predictive performance. A total of 455 datasets from previous research papers are employed for assessment. Dimensionless parameters Froude number $\left( {Fr = \frac{U}{{\sqrt {gy} }}} \right)$, Pier Froude number $Fr_{P} = \frac{U}{{\sqrt {g^{\prime } D} }}$, and the ratio of scour depth to pier diameter $(\frac{\text{y}}{{\text{D}}})$ are carefully selected as influential model inputs through dimensional analysis and the gamma test. The results highlight the superior performance of the SVM model. In the training phase, it exhibits an RMSE of 0.1009, MAE of 0.0726, R² of 0.9401, and S_DDR of 2.9237. During testing, the SVM model shows an RMSE of 0.023, MAE of 0.017, R² of 0.984, and S_DDR of 5.301. Additionally, it has an average error of − 0.065 and a total error of − 20.642 in the training set and an average error of − 0.005 and a total error of − 0.707 in the testing set. Conversely, the M5 model exhibits the lowest accuracy. The statistical metrics unequivocally establish the SVM model as significantly outperforming the experimental models, placing it in a higher echelon of predictive accuracy.

Introduction

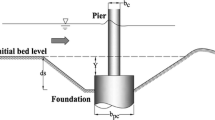
In the realm of river engineering, scour presents itself as a formidable challenge, instigating the gradual erosion and degradation of bridge structures. Numerous accounts substantiate erosion's role as a catalyst for the deterioration of bridges. Consequently, the precise estimation of bridge scour depth assumes paramount importance. Despite the multitude of diverse investigations into bridge pier scour depth, its inherent complexity underscores the significance of formulating precise simulators, a pursuit that commands considerable attention from both researchers and engineers alike. Within the USA, the primary contributors to bridge damage have been identified as scouring and flooding, as attested by numerous sources (Wardhana and Hadipriono 2003). The Austrian Federal Railways (BBB) experienced substantial financial losses amounting to approximately USD 113 million due to flooding events coupled with bridge collapses (Kellermann et al. 2016). Additionally, the projected expenditure for mitigating scour risk across Europe from 2040 to 2070 is estimated to reach USD 611 million per annum (Nemry and Demirel 2012). Given its integral role, this critical infrastructure component underscores the prominence of research endeavors focusing on augmenting safety during the design phase and minimizing the likelihood of bridge failures. In this context, researchers have introduced a range of experimental equations, a selection of which is displayed in Table 1. The review of existing literature demonstrates that over the recent decades, a variety of mathematical equations have been proposed to forecast the scour depth around bridge piers. However, these equations, often rooted in empirical observations, are fraught with numerous limitations (Brandimarte et al. 2012). Furthermore, their efficacy is typically confined to specific experimental conditions (Bateni et al. 2007). Mueller and Wagner (2005) undertook an assessment of 22 mathematical equations using field data, revealing a consistent trend of overestimating scour hole dimensions in comparison with actual measurements. Similarly, Landers and Mueller (1996) conducted a comparative analysis of five empirical formulas for bridge pier scour prediction based on field data, concluding that none of the selected formulas yielded accurate estimations of scour depth. Gaudio et al. (2010) conducted a comparative study involving six design formulas for predicting scour depth, juxtaposing the results with field data. Their investigation disclosed that all utilized formulas generated predictions that were deemed unreasonably inaccurate. Multiple other scholars have documented the deficiencies inherent in experimental-based formulations when it comes to forecasting the depth of scour around bridge piers (Rahimi et al. 2020).

Table 1 Some empirical formulae used for estimating pier scour

In response to these challenges, researchers have increasingly directed their efforts towards leveraging artificial intelligence (AI) techniques to enhance the accuracy of pier scour depth prediction. Within this context, machine learning methods (MLMs), which constitute a prominent subset of AI methodologies, have garnered significant interest among researchers in the realm of engineering prognostication. MLMs operate by scrutinizing datasets, with a specific emphasis on identifying interrelations among input, internal, and output variables, all while circumventing the need for explicit comprehension of the system's underlying physical mechanisms (Qaderi et al. 2020). Table 2 displays the compilation of a literature review encompassing diverse MLMs techniques employed for the modeling of scour depth around bridge piers.

Table 2 A brief literature review on scour depth prediction using DDMs

The primary impetus behind this research stems from the prowess and prospective applications of MLMs. In pursuit of this objective, the current study systematically employed extensive datasets derived from empirical experiments conducted within various laboratory flume settings. These datasets encompassed a diverse spectrum of sediment gradations and coarse material fractions. The resultant data points exhibit a substantial breadth of variability, thereby facilitating the utilization of the SVM, the GEP, the ANN and empirical equations for the purpose of predicting scour depths in the vicinity of cylindrical bridge piers. To discern the optimal predictive models, a comprehensive analysis involving statistical indices has been undertaken.

Material and methods

The forthcoming research endeavor will encompass a systematic sequence of steps, characterized by the following methodological delineations: (i) data collection and nalysis, (ii) dimensional analysis, (iii) sensitivity analysis, (iv) identification of key inputs, (v) implementation of prescribed models, (vi) output analysis. This structured framework encapsulates the logical progression of the research endeavor, designed to yield robust and substantiated findings. The methodology employed in the current investigation for the prediction of bridge pier scour depth is elucidated through the schematic representation depicted in Fig. 1.

Fig. 1

Flowchart applied for the present paper to opt superior predictions

Dataset complied

The data employed in the current investigation were sourced from pre-existing studies documented in the literature, specifically conducted under conditions characterized by clear water. These studies encompass a diverse array of laboratory flumes and field data, incorporating a wide spectrum of sediment compositions and hydraulic flow scenarios. In totality, a dataset comprising 455 dependable data points was curated and subsequently utilized as the foundation for the present research endeavors. It is noteworthy that among this total, 168 datasets pertain to field data, while 287 datasets pertain to laboratory data. Table 3 delineates the statistical metrics corresponding to the datasets associated with each respective reference. Within this tabular representation, the variables are defined as follows: D signifies the diameter of the pier, Y pertains to the flow depth, U denotes the flow velocity, U_c represents the critical velocity, D₅₀ encapsulates the average size of sediment particles, and S embodies the scour depth. The abbreviations Max, Min and S.D stand for the maximum value, minimum value, and standard deviation of the datasets, respectively. As elucidated in the detailed descriptions outlined in Table 3, the simulation of relative scour depth is achieved through a fusion of laboratory and field data. To mitigate the impact of numerical scale variations, all model inputs have been normalized to a standardized range between zero and one.

Table 3 Statistical characteristics of collected datasets

Dimensional analysis

The scour hole depth can be elucidated through the consideration of three primary categories: (i) flow conditions, (ii) sediment characteristics, and (iii) bridge pier geometry. The subsequent equation can be formulated as follows:

$$ S = F(g,\;\rho ,\;U,\;U_{c} ,\;y,\;\mu ,\;D,\;D_{50} ,\;\rho_{s} ) $$

(15)

In the equation provided, where g represents the acceleration due to gravity, ρ denotes the density of water, ρ_s signifies the density of sediment, U stands for the mean velocity of the flow, U_c represents the critical velocity of sediment particles, y represents the flow depth, μ denotes the dynamic viscosity of water, D stands for the diameter of the bridge pier, and D₅₀ represents the mean diameter of sediment particles. As duplicate parameters, three D, U, and ρ parameters were opted to extract dimensionless parameters using the Pi-Buckingham theory. The outcome of the dimensional analysis can be articulated as follows:

$$ \frac{S}{D} = G\left( {\frac{U}{{U_{c} }},\; \frac{y}{{D_{50} }},\;\frac{U}{{\sqrt {gy} }},\;\frac{{U_{c} }}{{\sqrt {gD_{50} } }},\;\frac{U}{{\sqrt {gD} }},\;\frac{\rho Uy}{\mu }} \right) $$

(16)

Here $\frac{\text{U}}{\sqrt{\text{gy}}}$ is the Froude number (Fr) of the flow, $\frac{{\text{U}}_{\text{c}}}{\sqrt{{\text{gD}}_{50}}}$ is the densimetric Froude number (Fr_D) of the sediment particle, $\frac{\text{U}}{\sqrt{\text{gD}}}$ is the Froude number (Fr_p) of the bridge pier, $\frac{\rho Uy}{\mu }$ is the Reynolds number (Re) of the flow. Due to the presence of turbulent flow conditions, the Re was excluded from the analysis. Additionally, the parameter $\frac{\text{U}}{{\text{U}}_{\text{c}}}$ was omitted, given the inclusion of the Fr and Fr_D. Consequently, Eq. (18) is simplified to the following form:

$$ \frac{S}{D} = G\left( {\frac{y}{D},\;Fr,\;Fr_{D} ,\;Fr_{P} ,\;\frac{y}{{D_{50} }}} \right) $$

(17)

Gamma test

As elucidated by Koncar (1997), the gamma test is a nonparametric statistical method employed to estimate an output by identifying the optimal set of input–output datasets based on the best mean square error values. This method is introduced as a suitable approach for determining the most effective combination of diverse input variables to accurately describe the output. In this method, the dataset is supposed as $\left\{ {\left( {{\text{x}}_{{\text{i}}} {,}\;{\text{y}}_{{\text{i}}} } \right){, }\;{1} \le {\text{i}} \le {\text{M)}}} \right\}$, where the input vectors $x_{i} \in R^{m}$ are m dimensional vectors and corresponding outputs $y_{i} \in R$ are scalars. The vectors x influences the output y. The association among the inputs and output variables is defined by the following equation:

$$ y = Gx + \Gamma $$

(18)

Here G and Γ represent gradient and interception of the regression line (x = 0), respectively, and y is output. Smaller values of G and Γ indicate that the corresponding input variables are more suitable. In addition to these two criteria, an indicator denoted as $V - Ratio = \frac{\Gamma }{{\sigma^{2} (y)}}$ where Γ represents the gamma function and $\sigma^{2} (y)$ is the output variance, is employed to identify the optimal input parameters. The values of V-Ratio range from 0 to 1. A V-Ratio value closer to zero for each input parameter signifies the effectiveness of that particular input. The various combinations of input variables have been delineated following the format introduced by Mask (Malik et al. 2021). Since Eq. (19) incorporates five dimensionless parameters, the Mask representation employs five digits corresponding to the five parameters: $\frac{\text{y}}{{\text{D}}}$, Fr, Fr_D, Fr_p and $\frac{\text{y}}{{\text{D}}_{50}}$, respectively. In the representation provided, the digits ’1’ and ‘0’ signify whether an input is included (‘1’) or not included (‘0’). Therefore, '10,100' indicates that $\frac{\text{y}}{{\text{D}}}$ and Fr_D are employed as inputs, while ‘11,111’ indicates that all five parameters are utilized as inputs. As previously mentioned, the most favorable model is characterized by the lowest values of Γ, G, and V-Ratio. It is important to highlight that, owing to the distinct ranges of variation for each parameter, all analyses have been conducted using normalized data, as described by the following equation:

$$ x_{normal} = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }} $$

(19)

Here x_min and x_max are the minimum and maximum values of variable x, and x_normal is the normalized value of x_i. Table 4 displays the outcomes of the gamma test based on Eq. (19). From the data presented in Table 4, it is evident that the sixth model, which includes the parameters $\frac{\text{y}}{{\text{D}}}$, Fr and Fr_D (11,100), demonstrates the most favorable test results, characterized by the lowest values of Γ (0.052), G (0.372), and V-Ratio (0.305). Table 5 presents a brief statistical characteristics of input and output parameters. An overall graphic view for scour depth variation has been illustrated in Fig. 2.

Table 4 Gamma test result for different input variables

Table 5 Summary of statistical description of parameters included

Fig. 2

A 3D view of scour depth mapping

Overview of MLMs involved

A general view of the GEP

Proposed by Ferreira (2001), the GEP constitutes a genetic algorithm that operates by managing a populace of individuals. These individuals are selected based on their fitness and subsequently subjected to genetic diversity through the application of one or more genetic operators, as expounded upon by Mitchell (1996). The GEP amalgamates diverse components, encompassing mathematical and logical expressions, polynomial constructs, decision trees, and assorted operators. The programming of GEP entails the utilization of linear chromosomes, which are articulated through expression trees (ETs). The procedural depiction of GEP's operational sequence is delineated in Fig. 3, as illustrated by the GEP simulation flowchart.

Fig. 3

Flowchart of the GEP

The initial phase involves generating an inaugural population derived from equations that constitute random amalgamations of a predefined array of functions. This assemblage encompasses mathematical operators within equations, alongside terminating elements like problem variables and constants. Proceeding to the subsequent stage, each constituent of the population is evaluated based on established fitness criteria. Subsequently, the third stage encompasses the generation of a fresh population via the deployment of equations. Advancing to the fourth stage, the preceding procedure is reiterated iteratively with the aim of attaining the highest possible yield of outcomes.

A general view of the SVM

Conceived by Vapnik (1995), the SVM stands as a nonlinear search algorithm employed for classification purposes, grounded in the structural risk minimization principle derived from statistical learning theory, as elucidated by Qaderi et al. (2020). Originally introduced for classification tasks, this algorithm underwent subsequent development, leading to an extended version designed for non-parametric regression analysis, referred to as Support Vector Regression (SVR). At its core, the SVM draws upon the foundation of statistical training theory. Analogous to regression equations, the linkage between the dependent variable Y and the independent variables x_i is formalized as an algebraic equation, encompassing a noise component, as depicted below:

$$ Y = f\left( x \right) + noise = \left[ {\mathop \sum \limits_{i = 1}^{D} w_{i} .\varphi_{i} (x) + b} \right] + noise $$

(20)

where $\varphi_{i} (x)$ is the kernel function, b is the characteristics of the regression function, and W_i is the weighted vectors. Table 6 documents distinct categories of kernel functions. Notably, empirical evidence stemming from multiple studies has substantiated the superior efficacy of the radial basis function (RBF) over alternative kernel functions, as demonstrated by Dibike et al. (2001). Within the realm of RBF, two pivotal tuning parameters, specifically the penalty parameter denoted as C and the epsilon parameter symbolized as ε, are identified and calibrated with the aim of optimizing performance outcomes.

Table 6 Types of kernel functions

A general view of the M5

Model trees (MTs) are employed as a strategic approach to address intricate problems by partitioning them into more manageable subproblems. This technique entails the division of the parameter space into distinct subspaces, subsequently constructing an Adept linear regression model for each subset, referred to as a terminal, node, or leaf. The M5 algorithm, designed for the creation of model trees, establishes a hierarchical tree structure, frequently binary in nature. This structure encompasses splitting rules at nonterminal nodes and expert models at the terminal leaves. The M5 algorithm employs a divide-and-conquer principle, as visually depicted in Fig. 4.

Fig. 4

Splitting the input space X1 × X2 by M5

Within the M5 algorithm, the standard deviation (SD) functions as the designated criterion for performing splits based on class distinctions. Furthermore, it computes the projected reduction in error resulting from evaluating each variable at the designated node. The formulation employed to calculate this reduction, known as the SDR, is central to the construction of the M5 model tree, and can be expressed as follows:

$$ {\text{SDR}} = {\text{SD}}\left( {\text{T}} \right) - \mathop \sum \limits_{{\text{i}}}^{ } \frac{{\left| {{\text{T}}_{{\text{i}}} } \right|}}{{\left| {\text{T}} \right|}} \times {\text{SD}}\left( {{\text{T}}_{{\text{i}}} } \right) $$

(21)

where T represents a set of examples that reach the node; T_i denotes the sets of examples that have the i-th outcome of the potential set; and SD represents the standard deviation.

A general view of the GBT

Statistically expounded upon by Breiman et al. (1984), Hastie et al. (2001), and De’ath and Fabricius (2000), contemporary decision trees (DTs) employ a strategic methodology for partitioning the predictor space into distinct rectangles. This process involves the sequential application of rules to delineate regions characterized by the highest degree of homogeneity in their responses to predictor variables. Illustrated in Fig. 5, each of these regions is associated with a constant value. In the context of classification trees, this constant value represents the most probable class. Conversely, for regression trees, the constant value signifies the mean response of observations within that specific region. It is noteworthy that regression trees operate under the assumption of errors conforming to a normal distribution, as stipulated by Hastie et al. (2001).

Fig. 5

Single DT with a response Y and two predictors X₁ and X₂ and split points t₁, t₂, … (left panel); prediction surface (right panel)

To improve the DTs precise, boosting methods have been developed based on this idea that it is easier to find and average many rough rules of thumb, than to find a single, highly accurate prediction rule (Schapire 2003). Gradient boosting is one of the common boosting method that a DT of fixed size is utilized as a base learner to improve fitting quality of every base learner, so-called gradient boosting tree, GBT. In the GBT, each subset tree is trained primarily with data that has been erroneously predicted by the previous tree. This makes the model more focused on complex cases and less on issues that are easy to predict (Breiman 1984).

A general view of the MARS

Developed by Friedman (1991) as a nonparametric regression model, the MARS is an algorithm with remarkable performance to estimate and simulate the interaction between input and target parameters of a linear or nonlinear continuous dataset. The MARS system fits an adaptive nonlinear regression model using multiple piecewise linear basis functions hierarchically ordered in consecutive splits over the predictor variable space. In other words, it is a high-precision technique for modeling systems which is based on the dataset. The generalized form of the MARS model can be expressed as follows:

$$ y = f(x) = c_{0} + \mathop \sum \limits_{n = 1}^{n} c_{N} H_{kN} (x_{\nu (k,n)} ) $$

(22)

$$ H_{kN} (x_{\nu (k,n)} ) = \mathop \prod \limits_{k = 1}^{K} H_{kN} $$

(23)

where y is the output parameter and c_o and N are the constant, the number of basic functions, respectively. $H_{kN} (x_{\nu (k,n)} )$ is basis function where $x_{\nu (k,n)}$ is the predictor of the k-th of the m-th product.

A general view of the MLP

MLPs represent a fundamental and versatile class of the ANN that have found widespread application in various fields. The MLPs are a type of feedforward artificial neural network characterized by their layered structure. Their architecture includes three main parts as follows: (i) input layer; (ii) hidden layer; and (iii) output layer. The input layer of an MLP receives the initial data or features and transmits them to the hidden layers. Each neuron in the input layer corresponds to a feature in the input data. MLPs can have one or more hidden layers between the input and output layers. These hidden layers contain neurons (or nodes) that apply weighted sums and activation functions to their inputs. The number of hidden layers and neurons in each layer is a crucial architectural choice. The output layer produces the final result or prediction of the network. The number of neurons in the output layer depends on the nature of the task. MLPs are trained using supervised learning, where they learn to map input data to target output values. The most common training algorithm for MLPs is backpropagation, coupled with gradient descent or its variants. This process involves adjusting the weights and biases of the neurons to minimize a predefined loss function, typically mean squared error for regression tasks and cross-entropy for classification tasks. Neurons in MLPs use activation functions to introduce nonlinearity into the model. Common activation functions include sigmoid, hyperbolic tangent (tanh), and rectified linear unit (ReLU). The choice of activation function can significantly impact training and model performance.

NLR models

Various empirical and experimental formulas were proposed to estimate scour hole depth base on flow, sediment, and bridge pier characteristics. The formulas that are more compatible with collected data in this research work have been presented in .

Table 7 The formulas listed in.

Table 7 Opted formula to predict scour hole depth

Table 7 are used to compare performance between experimental models and AIs.

Analyzing performance through statistical metrics

The performance of DDMs and empirical models is appraised using root-mean-square error (RMSE), mean average error (MAE), coefficient of determination (R²). These indices are defined as follows:

$$ RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{N} (O_{i} - P_{i} )^{2} }}{n}} $$

(26)

$$ R^{2} = \left[ {\frac{{N\left( {\mathop \sum \nolimits_{i = 1}^{N} O_{i} P_{i} } \right) - \left( {\mathop \sum \nolimits_{i = 1}^{N} O_{i} )(\mathop \sum \nolimits_{i = 1}^{N} P} \right)_{i} }}{{\sqrt {\left[ {N\mathop \sum \nolimits_{i = 1}^{N} O_{i}^{2} - \left( {\mathop \sum \nolimits_{i = 1}^{N} O_{i} } \right)} \right]\left[ {N\mathop \sum \nolimits_{i = 1}^{N} P_{i}^{2} - \left( {\mathop \sum \nolimits_{i = 1}^{N} P} \right)_{i} } \right]} }}} \right]^{2} $$

(27)

$$ MAE = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {O_{i} - P_{i} } \right|}}{N} $$

(28)

Here O and P are observed and predicted values of scour depth, respectively, and N is the total number of the dataset. Aforementioned indices represent average error values of the implmented models. To rectify this fault, the developed discrepancy ratio (DDR) statistic has been represented:

$$ DDR = \frac{Predicted \;value}{{Observed\; value}} - 1 $$

(29)

For better judgment and visualization, the Gaussian function of DDR values should be illustrated in a standard normal distribution. To this end, firstly, the DDR values of scour depths must be standardized and then using Gaussian function the normalized value of DDR (S_DDR) is calculated. Secondly, the values of S_DDR are plotted against standardized values of scour depth (Z_DDR). At Z_DDR vs. S_DDR graph, more tendencies in error distribution to the centerline and larger values of S_DDR have more precision (Noori et al. 2010).

Results and discussion

Using performance evaluation metrics, the simulation accuracy of each DDMs has been assessed and is presented in Table 8. This table provides a comprehensive overview of the performance of DDMs during both their training and testing phases. The data have been partitioned into a 70% training set and a 30% testing set. In addition to the statistical metrics delineated in Table 8, an examination of the residual distribution and the alignment between observed and calculated data, as depicted by the compliance curve, has been employed to assess the fidelity of the model simulations. In this context, Table 9 showcases several key statistical properties pertaining to the residual errors associated with each model's output.

Table 8 The outcomes assessment metrics of the DDMs included

Table 9 A summary of residuals for DDMs involved

In reference to Table 8, the performance indices (RMSE, MAE, R², DDR_max) for the SVM model during the training and testing stages are (0.1009, 0.0726, 0.9401, 2.9237) and (0.023, 0.017, 0.984, 5.301). Furthermore, the associated hyperparameters for the SVM model, specifically the setting parameters C, ε and γ, are set to 63, 0.5, and 0.2, respectively. Additionally, the radial basis function (RBF) kernel function has been selected as the kernel function for the SVM model. The error variation range exhibits fluctuations within the span of -0.366 to 0.076 throughout the training phase, and a narrower range of − 0.084 to 0.065 during the subsequent testing phase (Table 9). Furthermore, noteworthy is the substantial decrease in the mean error value, which decreases sharply from − 0.065 in the training phase to an analogous value of − 0.005 in the test phase. This dramatic reduction is further underscored by the total error count diminishing markedly, plummeting from an initial − 20.642 during the training phase to a mere − 0.707 in the test phase. The tabulated data unequivocally establish that this model possesses the most favorable statistical indices related to errors, signifying its unequivocal superiority over the other models. Figure 6 depicts the graphical representation of data fitting for the SVM model, illustrating its conformity with the observed data and the distribution of residuals. The salient observation and overarching inference gleaned from this graphical representation are that the model's precision is notably conducive for diminutive scour values. Furthermore, it is noteworthy that the model exhibits higher errors when dealing with larger datasets.

Fig. 6

Distribution of dataset and residuals for the SVM

The performance metrics are RMSE = 0.2229, MAE = 0.1674, R² = 0.7796, DDR_max = 1.2109 for the training phase and RMSE = 0.114, MAE = 0.071, R² = 0.872, DDR_max = 1.553 for the testing phase. These performance indicators have been computed based on the setting parameter values specified in Table 10. The structural representation of the GEP model, including the functions utilized, is visually represented in the form of a tree expression in Fig. 7. Additionally, the specific values of the constants employed in Fig. 7 are as follows: G1C0 = 9.322418, G1C1 = 3.138397, G2C0 =  − 0.491638, G2C1 = 2.819794, G3C0 = 0.961823, G3C1 = 5.220947. This observation suggests a tendency for overestimation within the GEP model. Reffering to Table 9, the error fluctuation range observed during the training period spans from − 0.674 to 0.235, while in the subsequent test phase, it narrows to a range of − 0.639 to 0.182. This marked reduction is vividly apparent in the average error values, diminishing notably from − 0.142 in the training phase to − 0.055 in the test phase. Such a discernible trend is further corroborated by the total error count, which undergoes a substantial decline, decreasing from an initial − 45.456 during training to − 7.483 in the test phase. With regard to the performance evaluation of the GEP model, the residual distribution and the alignment between observed and predicted data are visually presented in Fig. 8. Notably, it becomes apparent from this figure that the data do not adhere to the assumptions of the SVM model. Furthermore, the distribution of residual in the GEP exhibits a resemblance to the SVM model, particularly in the region characterized by predominantly negative values.

Table 10 Setting parameters of GEP to predict scour depth

Fig. 7

Tree expression of the GEP output

Fig. 8

Distribution of dataset and residuals for the GEP

The M5 and GBT models exhibit notably diminished accuracy relative to the other models under examination. In the training phase, the M5 model registers values of 0.5129 (RMSE), 0.3583 (MAE), 0.5348 (R²) and 0.5343 (DDR_max), while in the testing phase, it yields values of 0.284 (RMSE), 0.183 (MAE), 0.698 (R²) and 0.591 (DDR_max). In contrast, the GBT model demonstrates similar trends with values of 0.3667 (RMSE), 0.2599 (MAE), 0.6708 (R²) and 0.7579(DDR_max) during the training phase, and values of 0.125 (RMSE), 0.084 (MAE), 0.819 (R²) and 1.147 (DDR_max) in the testing phase. Figure 9 provides a visual representation of the output structure of the M5 model, illustrating its performance during both training and testing phases.

Fig. 9

The output of the M5 model through the training and the testing phases

For the M5 model, a notable contrast exists between the minimum and maximum error values, which range from − 1.931 to 0.459 during the training period and from − 1.611 to 0.157 in the test phase (Table 9). This discrepancy is further emphasized by the average error values, which stand at − 0.286 in the training phase and − 0.162 in the test phase. Remarkably, the cumulative errors for this model exhibit substantial magnitudes, amounting to − 593.91 during training and − 21.830 during testing. In the case of the GBT model, the range of error fluctuations spans from − 1.220 to 0.365 during training and from − 0.591 to 0.325 in the test processes. Notably, the total error value decreases significantly, with a reduction of nearly tenfold, declining from -68.893 during training to − 6.917. Notably, Figs. 10 and 11 reveal the conspicuous lack of alignment between observed and computed data, underscored by the substantial residual error in both models. In the presented figures, the disparity between the observed and computed values becomes readily apparent, particularly in datasets characterized by substantial values. Notably, when assessing the comparative performance of the M5 and GBT models, it is evident that the latter yields outputs with a higher degree of relative accursacy. Moreover, the conspicuous presence of overestimation is unmistakably evident in both of these models.

Fig. 10

Distribution of dataset and residuals for the M5

Fig. 11

Distribution of dataset and residuals for the GBT

The accuracy assessment of the MARS model outputs is predicated on several statistical indicators, including RMSE, MAE, R², and DDR_max. In the training phase, these indicators yield values of 0.2022, 0.1441, 0.8373, and 1.4324, respectively. In the test phase, corresponding values are 0.090, 0.057, 0.917, and 1.883, respectively. The relative scour depth can be computed using the following mathematical relationship, with specific details of the BFs provided in Table 11:

$$ \frac{{D_{s} }}{Y} = 0.006500112 + \mathop \sum \limits_{i = 1}^{8} c_{N} H_{kN} (X) $$

(30)

Table 11 The MARS model constructed BFs with their corresponding coefficients

The values 0.156 and − 0.716 denote the upper and lower bounds of errors observed during the training period, while during the test phase, the range contracts − 0.389 and 0.130, respectively (Table 9). A noteworthy decrease in the cumulative error is evident, with a reduction of nearly eight-fold, transitioning from − 41.629 during the training phase to − 5.501 during testing, underscoring the model's improved performance. Figure 12 illustrates the output of the MARS model, representing both the distribution of residual errors and the alignment with observational data, presented for scrutiny throughout the training and test phases.

Fig. 12

Distribution of dataset and residuals for the MARS

The performance evaluation indicators for the MLP model are derived from the MLP architecture with a configuration of 3 input nodes, 10 hidden nodes, and 1 output node. Activation functions employed are Tanh for the hidden layer and Identify for the output layer. The computed performance metrics, including (RMSE, MAE, R², DDR_max) indices are reported for both training and testing phases. These metrics yield values of (0.1545, 0.1116, 0.8781, 1.8315) for the training dataset and (0.058, 0.041, 0.964, 2.924) for the testing dataset. Furthermore, a visual representation of the MLP model's output is depicted in Fig. 13. Upon revisiting Table 9, it becomes evident that, in the case of the MLP model, the fluctuations in error values during the training period span from − 0.513 to 0.137, while during the test period, they range from − 0.291 to 0.019. Furthermore, the mean error has witnessed a noteworthy reduction, declining from − 0.097 in the training phase to − 0.039 in the test phase. This performance enhancement is underscored by a 30% reduction in the total error index, as clearly indicated by the tabulated figures.

Fig. 13

Distribution of dataset and residuals for the MLP

In our comprehensive comparison of the the DDMs employed in this research, we leverage the distribution curve of observational and computational data plotted around the ideal 1:1 line, as illustrated in Fig. 14. Points situated closer to this line signify the relative superiority of a given model's output. Notably, the black filled dots within this figure represent the performance of the SVM model, which conspicuously stands out as the most superior among the models under consideration. This distinction is both clear and unequivocal. Furthermore, as an additional metric for comparing the data-driven models, we analyze the graphical characteristic of the DDR index, depicted in Fig. 15. The compactness of the curve in proximity to the vertical axis and the heightened peak value along the vertical axis serve as indicators of a superior model. Remarkably, the SVM model maintains its supremacy throughout both the training and testing phases, firmly establishing its prowess in this context.

Fig. 14

Scatter plot 0f observed vs. predicted values of relative scour depth for DDMs

Fig. 15

The DDMs performance based on the DDR distribution

Regression equations

In this section, we assess the outcomes derived from the regression equations, as indicated in Table 7. The efficacy of predicting relative scour depth is presented in Table 12, which portrays the quality of these predictions. Within Table 12, it is evident that the statistical performance evaluation metrics for both models exhibit remarkable proximity to each other. However, the most substantial disparity lies in the value of the DDR_max index, where the the US, DOT (2003) equation achieves a notably higher score of 0.9931, in contrast to the Aksoy and Eski (2016) equations, which yield a lower score of 0.6863. Additionally, as per the data provided in Table 13, the residual indicators for both models manifest nearly identical values. Figure 16 visually portrays the distribution of residual in the experimental equations, revealing a pronounced non-compliance trend among data points with higher values. Moreover, Fig. 17 illustrates the distribution of data estimated by the emprical equations, with points closely clustered around the 1:1 line. This clustering, particularly evident in the predictions made by the US, DOT (2003) equation, underscores its relative superiority. Lastly, Fig. 18 reinforces the notion of the US, DOT (2003) equation’s superior performance in comparison with the equation presented by Aksoy and Eski (2016), as evidenced by the higher peak value along the vertical axis.

Table 12 The outcomes assessment metrics of the empirical predictors

Table 13 Summary of residuals for DDMs involved

Fig. 16

Distribution of dataset and residuals for empirical equations

Fig. 17

Scatter plot of observed vs. predicted values of relative scour depth for empirical equations

Fig. 18

The empirical equations' performance based on the DDR distribution

Conclusion

Scour phenomena around bridge piers are inherently intricate, necessitating a comprehensive understanding of their underlying mechanisms in order to effectively assess and predict scour hazards. To date, the development of precise methods for estimating scour depth remains an ongoing challenge. In the contemporary context, machine learning techniques have emerged as potent tools for predicting scour depth, leveraging experimental data to enhance our predictive capabilities in this domain. This study undertakes a comprehensive comparative analysis to evaluate the efficacy of various DDMs, specifically the SVM, the GEP, the MLP, the GBT, The M5, the MARS and two experimental equations, in the computation of scour depth around circular bridge piers. The outcomes of this investigation, while affirming the capacity and potential of DDMs in forecasting the scour depth of bridge piers, exhibit a notably enhanced relative precision in comparison to alternative models. Sequentially, the MLP, the MARS, the GEP, the GBT and the M5 models have ascribed themselves to subsequent ranks of the SVM. For the purpose of juxtaposing and assessing the relative accuracy of the results derived from DDMs, empirical equations were employed to assess the scour depth of bridge foundations. The precision of the outputs generated by this subset of equations demonstrates their occupancy of lower echelons when ranked against the DDMs. In a holistic appraisal, it can be posited that both categories, namely DDMs and empirical equations, exhibit proficiency in scour depth prediction. Nonetheless, the utilization of AI-based models yields more precise outcomes, as elucidated by the findings expounded by researchers in Table 2, albeit predicated upon the availability of an extensive repository of recorded data encompassing both independent and dependent variables, thereby serving as a preliminary and indispensable prerequisite for the application of these models.