Introduction

Floods are among the costliest natural hazards experienced in most of the places in the world, which results in heavy losses of life and economic damages (Gao et al. 2018). Regional flood frequency analysis (RFFA) is an especially used method for estimating flood risk at target locations in river basins where streamflow measurements are either limited or unavailable (Griffis and Stedinger 2007; Leclerc and Ouarda 2007; Zaman et al. 2012, Smith et al. 2015 and Lotfirad et al. 2018) The first RFFA was undertaken by the USGS in New England (Kinnison and Colby 1945). Lately, RFFA has received significant heed for design and management of water substructures such as dams, reservoirs, and bridges to slight flood risks and hence financial devastations. Much of this attention has occurred in response to water-related hazards such as the flood in regions where minute or no data is available on peak flows such as the Indus floods in East of Iran.

RFFA has been used as a crucial tool for many applications for example (i) water substructure, (ii) flood preservation projects, (iii) land cover planning, and other hydrologic studies. The regional techniques consist of a multivariate statistical structure derived from catchment characteristics data (Rao and Srinivas 2008). In this process, the region of influence approach can be formed where some catchments are pooled together based on vicinity in geographic. Consequently, an optimum region is made based on some objective function (Holmes et al. 2002; Aziz et al. 2010).

The relationship among flood flow values, physiographical and/or morphological characteristics of a catchment is a fundamental framework for RFFA. Various methods such as multivariate regression method (MRM), square grids method (SGM) and hybrid method (HM) have been developed in the literature for RFFA; each approach has its advantages and disadvantages. Among these methods, MRM has been widely used and presented in previous studies (Golestani et al. 2010; Malekinezhad et al. 2011; Latt et al. 2014).

Recently, data-driven models have been widely adopted in hydrological studies. Data-driven models can handle the nonlinearity and uncertainty in hydrological data very effectively. These methods are extensively used for rainfall-runoff modeling, water resource management modeling, and suspended sediment modeling take; for example, Kumar et al. (2015) provide the details of the application of data-driven models in regional flood frequency estimation which is explored. Regional flood frequency relationships are developed employing data-driven models viz. ANN and FIS for lower Godavari subzone 3(f) of India and the same have been compared with the regional relationships derived using the L-moments approach.

Recently, the data-driven models such as random forest (RF), fuzzy computing techniques and M5 decision tree, in complex modeling of the flood, have been developed by Solomatine and Xue (2004); Aziz et al. (2014); Sehgal et al (2014); Kumar et al (2015); Latt et al. (2015); Deo and Şahin (2016); Esmaeili-Gisavandani (2017); Ghumman et al. (2018); Zahiri and Nezaratian (2020); Desai and Ouarda (2021); Adib et al. (2022); Jahangir et al. (2022). Among the numerous data mining techniques, ANFIS is the most widely used approaches in various water-related areas. Being an accurate predictive tool, the ANFIS technique has, however, an inherent disadvantage that often results in hesitating to interpret their outputs. This is because of being a black box and consequently the nature of their solution is hazy. There might be a variation between networks of the same architecture trained on the same dataset due to the arbitrary nature of the internal representation. (Witten and Frank 2000). Srinivas et al. (2008); Aziz et al. (2017); Esmaelili-Gisavandani et al. (2017); Sharifi Garmdareh et al. (2018), and Zalnezhad et al. (2022) attempted to shed light on the structure of ANFIS using regional flood analysis and the methods of recovering rules. However, few studies have been used the application of the M5 algorithm and random forest in RFFA. Therefore, in this study, random forest and M5 algorithms were used to investigate peak flow and compare ANFIS with the multivariate regression method. The most advantage of M5 and RF have been classified by being induced into linear patches; these models provide a representation that is reproducible and understandable by practitioners. (Solomatine and Xue 2004; Jothiprakash and Kote 2011). The target of RFFA is predicting river peak flow associated with various return periods in ungauged catchments and also reduce uncertainty to evaluate the flooding (Merz and Blöschl 2008; Zaman et al. 2012; Shu and Ouarda 2012; Leščešen et al. 2019). The objectives of this study are two-fold. Firstly, the aim is to estimate the RFFA utilizing the random forest and M5 algorithms. Secondly, the goal is to estimate flood occurrences in data-deficient catchments within the western region of Iran.

Materials and methods

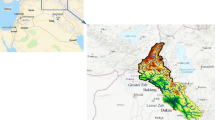
Out of eighty-nine stream gauges, thirty-two stations were used due to the availability of data. The data were obtained for the period of 1987-2018. The study area, including thirty-two stream gauges, is located in the west of Iran. From the homogeneous stations, twenty-seven stations were used for calibration and five stations for validation of the models (Fig. 1b). In fact, five stations were used for validation which was not used for the modeling and after making model, each data-driven model validated with these stations. To approach a unique model, the return period was taken into account as an independent factor. The study considered the annual maximum instantaneous peak flow. Kolmogorov–Smirnov test in EasyFit software 5.6 was used to estimate peak flow with different return periods based on the best distribution function (Shokouhifar et al. 2022).

Fig. 1
figure 1

Location of the Karkheh basin in Iran

Full size image

Study area

The Karkheh River basin is located in the west of Iran (Fig. 1a). The Karkheh River basin covers 51,230 square kilometers in parts of six Iranian provinces. The Karkheh river length is approximately 900 km. (Fallah-Mehdipour et al. 2020). This study considers RFFA using three data-driven models (M5, RF and ANFIS) and a multivariate regression method in ungauged catchments. The further detail of Karkheh Basin could be found in many papers (see, e.g., Gheitasi 2016; Zamani et al. 2015).

Data

The following data were used in this study: (i) annual maximum instantaneous peak flow that was obtained from the Ministry of Energy of Iran and (ii) the physiographic characteristics of the catchment were extracted from the ALOS-PALSAR satellite with a spatial resolution of 12.5 m (https://asf.alaska.edu). The extraction of physiographic characteristics was carried out in the ArcGIS software 10.5.

The data utilized in this study, including the annual maximum flood (Q), ranges from 17.5 to 1337.8 m3/s. The flood discharge was calculated with a return period (T) of 2, 10, 100, 1000 years. Drainage areas (A) range from 8.17 to 26,187.02 km2. The range of the height of each sub-basin (H) is 1043 to 2621 m; the range of stream length (L) is between 4.77 to 420.82 km and catchment slope (S) varying from 8.14% to 37.67%. Table 1 presents the physiographic characteristics of the studied catchments.

Table 1 Descriptive statistics of physiographic characteristics
Full size table

Data-driven modeling

Data-driven modeling relies on relationships between measured data without a need for a priori knowledge of the physical system behavior (Jones et al. 2013; Ashrafzadeh et al. 2020; Biazar et al. 2020; Jafarpour et al. 2022). Once trained, data-driven modeling becomes a parametric description of the function. Out of several possible data-driven methods, ANFIS is the most widely used ones in water resource applications, whereas less attention has been directed toward the RF and M5 model trees. 70% of the data were used for training and 30% for testing in all models. A brief description of the methods mentioned above, is summarized as follows:

M5 model

M5 model is a data-driven model proposed by Quinlan (1992) and mainly employed in the realm of water science (Rahimikhoob 2014; Kisi and Kilic 2016; Kisi and Parmar 2016). Continuously, the final structure together with the dependent leaves is shown as a tree in Fig. 2b. The further detail of M5 model could be found in many papers (e.g., Farajpanah et al. 2020; Adib et al. 2023).

Fig. 2
figure 2

Schematic of M5Tree: a splitting the input space, b the resultant dendriform (Wang et al. 2017)

Full size image

Random forest

The RF method is nonparametric and belongs to the family of ensemble methods. The RF method consists of a set of regression trees used to reconstruct educational data. Typically, a set of basic training examples is formed. Combining three parameters in RF is essential. The first is how many trees should be created, the second is how many variables are involved in creating a node for each network, and the third parameter is the size of the node, which indicates the depth of the regression tree created. One of the advantages of this method is that there is no need to prune the trees during modeling and classification (Esmaeili-Gisavandani et al. 2022).

ANFIS

Adaptive neuro-fuzzy inference system (ANFIS) could be a multilayer feed-forward network where each node performs a selected function on incoming signals (Jang 1993; Heddam 2014). An ordinary architecture of an ANFIS, during which a circle indicates a set node, whereas a square indicates an adaptive node, is shown in Fig. 3. The further detail of ANFIS could be found in many books (e.g., Azar 2010; Esmaeili-Gisavandani 2017; Adib et al. (2021).

Fig. 3
figure 3

Sugeno ANFIS system equivalent to the system

Full size image

Evaluation criteria

Normal root-mean-square error (NRMSE) and correlation coefficient (R2) were used to evaluate model performance:

$$R^{2} = 1 - \frac{{\sum {(Y_{i} - X_{i} )^{2} } }}{{\sum {(X_{i} - \overline{X}_{i} )^{2} } }}$$
(1)
$${\text{NRMSE}} = \frac{1}{{\overline{X}_{i} }}\sqrt {\frac{{\sum {(Y_{i} - X_{i} )^{2} } }}{n}}$$
(2)

where Xi and Yi are the observed and estimated values and \(\overline{{X_{i} }}\) are the average values of observation, and n represents the number of data. A comparison of the correlation coefficient and RMSE values recognizes a better performance. The best model has higher value of R2 and a smaller value of RMSE.

Results

According to Table 2, four combinations of input data were used in the MRM, ANFIS, M5 and RF models to peak flow with different return periods for regional flood frequency analysis (RFFA) (Table 3).

Table 2 The four combinations of input datasets
Full size table
Table 3 The ANFIS performance in different models
Full size table

ANFIS results

To calculate RFFA with the ANFIS model, for any combination, an optimum number of membership functions was specified based on trial and error. The best type of membership function was recognized from between bell-shaped (gbellmf), trapezoidal-shaped (tramf), triangular-shaped (trimf), Gaussian (gaussmf) and Gaussian 2 (gauss2mf) by repeated model training and testing based on every membership function number and type via trial and error. Based on the correlation coefficient (R2) and root-mean-square error (RMSE), combinations 4 (R2 = 0.92 and NRMSE = 0.851) is better performance than the others (Fig. 4).

Fig. 4
figure 4

The tree diagram generated by the M5 model for the case study

Full size image

M5 results

The M5 model tree does not require to set any user-defined parameters. In addition, the M5 model can provide the number of linear relations which can be easily used to predict the RFFA, as shown in Fig. 5.

Fig. 5
figure 5

Comparison of peak flow estimated by models in the validation phase

Full size image

As shown in Table 4, the M5 model results indicated that input combination 4 gave a better performance than the other combinations (R2 = 0.95 and NRMSE = 0.45). The tree relationships of the M5 model for the best combination of the inputs are presented in the appendix.

Table 4 Evaluation criteria for the M5 model
Full size table

RF results

As shown in Table 5, the RF model results indicated that input combination 4 gave a better performance than the other combinations (R2 = 0.96 and NRMSE = 0.223).

Table 5 Evaluation criteria for the M5 model
Full size table

As shown in Fig. 5, the peak flow values estimated by each model are compared. RF has the best performance in peak flow estimation, while MRM has the worst. Furthermore, most of the models underestimated the peak flow in the 2-year and 10-year return periods, while most overestimated the peak flow in the 100-year and 1000-year return periods.

As Fig. 6 illustrates performance of the used models in calibration (twenty-seven stream gauges) and validation (5 stream gauges) stages, according to the Taylor diagrams (Fig. 6), the performance of the RF model is the best. In the return periods of 2, 10, and 1000 years, the M5 model ranks second after the RF, but in the 100-year return period, the ANFIS model ranks second after RF.

Fig. 6
figure 6

Performance of RF, M5, ANFIS, and MRM in estimating flood frequency in five validation stream gauges at 2,10,100, and 1000 return periods

Full size image

Discussion

This study aims to provide a relatively simple method to estimate peak flow amounts in ungauged region based on their physiographic characteristics. To achieve this, data-driven models of varying natures were used. The MRM model is based on regression, the ANFIS model is based on fuzzy logic, the M5 model is based on classification, and the RF model is based on ensemble learning under supervision. Models require inputs such as area, stream length, basin slope, basin height, and return period number, which can all be derived from topography. Also, the best combination of inputs belonged to combination 4 with a higher correlation coefficient and lower NRMSE. Based on the excellent results obtained in estimating peak flow in the calibration and verification stages, particularly using the RF model, it is clear that this study is far more effective than similar studies whose inputs and modeling process were incredibly complex. It is evident from Fig. 6 that the models used for estimating peak flow had a favorable performance, especially the RF model, with better accuracy in the short-term return period of 2 and 10 years than in the long-term return period (100 and 1000 years).

RFFA makes a relationship between flood frequency and physiographical characteristics of catchments to estimate flood in ungagged regions like Rahman et al. (2020). In this regard, the performances of the RF and M5 tree network as piecewise linear functions, ANFIS and multivariate regression method were evaluated to estimate flood frequency in the ungagged sub-catchments like Vafakhah and Bozchaloei (2020).

A comparison of the correlation coefficient and root-mean-squared error values indicated an improved performance obtained from the data-driven model compared to traditional methods such as the multivariate regression (MRM) Method. However, the performance of the RF model is almost similar to the M5 and ANFIS models.

Conclusions

Knowing the magnitude of historical floods in a particular area is crucial for designing hydraulic structures. Small and medium watersheds often lack ground flow measurement stations due to the costs involved in building and maintaining them. In contrast, hydraulic structures need to be built on rivers in these areas in order to develop civil and agricultural activities. Therefore, the flood discharge design must be determined. This study used machine learning models to estimate the peak flow of ungauged watersheds.

The following model performance was found in this study:

The procreated dendriform structure of multi-linear models utilized in RF and M5 is comprehensible and straightforward to grasp for decision-makers. It also provides an honest overview of the relationships between the physiographic characteristics of the watershed;

The RF and M5 model permits to simply create a family of explainable models with a varied number of component models and thus varied strength and correctness;

Modeling with the RF and M5 are the fastest data-driven models (proceeding of data with RF and M5 is faster than ANFIS);

The information encapsulated in RF and M5 algorithms can potentially assist in variable selection and the evaluation of their relationships when processing data with other models. For instance, M5 can aid users in determining the sensitivity of the data.