Uplift pressure and hydraulic gradient in Sabalan Dam

Abstract

The present study investigates the effects of clay core thickness and cutoff wall depth on some of the design parameters in the Sabalan rock fill dam by the finite-element method using the SEEP/W software. Clay cores with various thicknesses and cutoff walls in different situations of dam foundations were tested. The results revealed that (1) the maximum hydraulic gradient in Sabalan dam foundation occurs in the cutoff wall; (2) the minimum hydraulic gradient can be found by changing the location of the cutoff wall, under the center of clay core; and (3) discharge reduction depends on the optimum position at heel of the core. As the permeability decreases and the depth of the cutoff wall increases, the hydraulic gradient in the cutoff wall increases. As the thickness of the clay core increases, hydraulic gradient and the seepage discharge decreases and the uplift pressure increases.

Introduction

Dam is a structure built across a stream, a river, or an estuary to retain water. Dams are built to provide water for human consumption, for irrigating arid and semiarid lands, or for use in industrial processes. They are used to increase the amount of water available for generating hydroelectric power, to reduce peak discharge of floodwater created by large storms or heavy snowmelt, or to increase the depth of water in a river in order to improve navigation and allow barges and ships to travel more easily.

The geographic location of the Iran and the need for constructing water storage dams force the decision-makers consider large and small dams as surface water collectors and flood control structures for proper use of river flows. Unusual seepage may pose some problems to the integrity of the dam, and any uncontrolled seepage may lead to the piping phenomenon and dam failure. Prediction of seepage in time and space and the consequent seepage path through the dam is important for planning and implementing technically and economically sound remedial stability measures (Tayfur et al. 2005). Seepage from the body and foundation of dams could be controlled using cores, cutoff walls and clay blanket in dam upstream.

Literature review shows that essential design parameters in embankment dam engineering are: uplift pressure, hydraulic gradient and discharge (seepage) through the dam.

When a dam rests on a porous material, such as sand or gravel, through which water can penetrates, there will be a seepage flow under the dam from the upstream side to the downstream side. Accompanying this flow, there will be an upward pressure acting on the horizontal base of the dam.

Such pressures have received considerable attention from design engineers. There have been important attempts to investigate, from laboratory models, the way in which this upward pressure varies across the base of the dam, and the way in which this pressure varies with head, depth of sheet-piling/cutoff wall. Recently, Salmasi et al. (2017) investigated uplift pressure under the trapezoidal concrete lined canals including drain pipes under the canal invert. Results showed that application of drain pipes under the canal bed at appropriate positions is effective in reducing groundwater depth and thereby reducing uplift pressures.

The hydraulic gradient is a vector gradient between two or more hydraulic head measurements over the length of the flow path. In other words, the potential drop between two adjacent equipotential lines divided by distance between them is known as hydraulic gradient. The quick condition occurs at a critical upward hydraulic gradient (i_c), when the uplift pressure (seepage force) just balances the buoyant weight of an element of soil. The critical hydraulic gradient is typically around 1.0 for many soils.

All dams have some seepage as the impounded water seeks paths of least resistance through the dam and its foundation. Seepage becomes a concern if it is carrying material with it and should be controlled to prevent erosion of the embankment, or foundation, or damage to concrete structures. If the seepage forces are large enough, soil will be eroded from the foundation and be deposited in the shape of a cone around the outlet. If these "boils" appear, professional advice should be sought immediately. Seepage flow which is muddy and carrying sediment (soil particles) is evidence of "piping," and is a serious condition that if left untreated can cause failure of the dam. Piping can most often occur along a spillway or other conduit through the embankment, and these areas should be closely inspected. Seepage from the dam body could be controlled using clay cores and cutoff walls.

Nazari Giglou and Zeraatparvar (2012) investigated the seepage of earth dams, taking into account geometrical and physical parameters like permeability, upstream and downstream slope of the dams. The results showed a significant effect of these parameters on the seepage from the earth dams. Salmasi and Mansuri (2013) carried out the effect of hydraulic conductivity ratio on seepage of earth dams with horizontal drain. Based on that study, if the filter is located away from upstream face, i.e., near the downstream toe, seepage is reduced but the saturated zone in downstream is increased. This phenomenon has negative effect on downstream slope stability. Hasani et al. (2013) analyzed seepage using Geo-studio software for Ilam earth dam. The results showed that average flow rate of seepage for Ilam dam is 0.836 L per second for the entire length of the dam. In another research, Farzampour et al. (2014) determined the optimum dimensions of the clay core for the Alavian Dam. In that study besides hydraulic parameters considerations (critical hydraulic gradient and uplift force), economic attentions were noticed. For this purpose, the SEEP/W and SLOPE/W software were used for numerical simulation. The results showed that the optimized clay core volume is decreased up to 33% compared to the current dimensions of the Alavian Dam Mansuri et al. (2014) studied the effects of different positions of the cutoff wall with different angles under dams on uplift pressure. The results of this study demonstrated that the inclined cutoff would reduce the uplift pressure higher than vertical cutoff. Asadi Sakhmarsi et al. (2014) and Mortazavi and Soleimani (2015) studied the seepage from earth dams using SEEP/W and SEEP-3D software. The results revealed that if the cutoff is located near the toe of the dam, it will be more effective in reducing exit hydraulic gradient. Heidarzadeh et al. (2015) studied numerical simulation of seepage from foundation of the Karkheh Dam. Outcomes showed that by the fixation of the relief wells in the downstream of the dam, safety factor of the downstream slope is increased to the safe value of 1.3.

Salmasi et al. (2015) studied the effect of relief wells in reduction of uplift pressure in homogeneous earth dams. They showed that in embankment dams with high potential of piping, providing of relief wells in downstream of dam have positive effect in uplift pressure decline. Salmasi and Nouri (2017) investigated the effect of upstream semi-impervious blanket of embankment dams on seepage. They used finite-elements method (FEM) to simulate the effect of blanket in reduction of seepage. Nourani et al. (2017) conducted a numerical investigation to find the optimum location for vertical drains in gravity dams. Drainage galleries are often use in gravity dams to reduce uplift force by collecting seeped waters from dam foundation. Jafari et al. (2019) carried out an investigation of granular filter under the bed of a canal. They demonstrated that application of filter envelop around drain pipes under the canal bed, reduces uplift force. This facility prevents any crack in canal lining.

The purpose of the present study is to investigate the effect of clay core thickness and cutoff wall below the clay core in Sabalan rock fill dam with a heterogeneous and permeable foundation on the hydraulic gradient, uplift pressure and seepage. This study is accomplished numerically with finite-element method (FEM) using SEEP/W software. In most of the designed earth dams, the cutoff walls (for reduction of seepage) are positioned in the central of the clay core at dam foundation. One of the present study goals is to test the other locations for cutoff walls in earth dam foundation. These locations can differ from heel to toe of the clay cores in dam foundation. In addition of seepage rates, different position of cutoff walls would influence on hydraulic gradient and uplift pressure too. This study tends to investigate numerically these parameters on a real dam. The selected dam is Sabalan rock fill dam located in Iran. The results of the numerical simulation would be provided using different dimensionless charts for guide lines of engineers.

Materials and methods

An overview about Sabalan rock fill dam

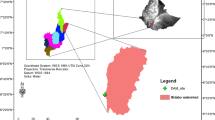
Sabalan (popularly known as Savalan) Dam is located at 55 km from the northwest of Ardebil and a distance of 40 km from northeast of Meshginshahr, Iran (Fig. 1). The purpose of constructing Sabalan rock fill dam is storage of 105 × 10⁶ m³ from Qara-Su river for irrigation of 15 thousand hectares of dry lands and orchards of Meshginshahr on both sides of the river, providing the drinkable water for Meshginshahr city up to 10 × 10⁶ m³ per year, flood control and creating jobs and reducing emigration.

Fig. 1

Location of the Savalan rock fill dam in Ardabil Province

Now Sabalan dam is under operation but some parts of its irrigation system are being constructed. In downstream of the dam, some of the important hydraulic structures related to irrigation system are:

• 1. Building of a trapezoidal main canal with a length of 12 km with concrete lining construction and implementation of geo-membrane sheet.

• 2. Construction of a flume with length of 6.3 km using reinforced concrete.

• 3. Constructing an inverted siphon with 2000-mm-diameter steel tubes at a length of 4.2 km with up to 30% slopes.

Governing equations

Seepage follows the Darcy’s law as Eq. 1:

$$q = - kAi$$

(1)

where q is the flow discharge (m³/s) through porous media, A is cross section of flow (m²), k is the hydraulic conductivity coefficient (m/s) and $i = \partial h/\partial s$ is hydraulic gradient (dimensionless). The governing equation for flow of water in porous media is Poisson’s equation (Eq. 2) which is a combination of continuity equation and Darcy's law.

$$k_{x} \frac{\partial h}{{\partial x}} + k_{y} \frac{\partial h}{{\partial y}} = q$$

(2)

where k_x and k_y are hydraulic conductivity in horizontal and vertical axes, respectively (m/s), h is the total water head (m). Equation 2 represents steady-state flow in soil which is independent of time. SEEP/W (a part of Geo-Studio software) uses FEM to solve the Poisson’s equation (Geo-Studio 2012).

In fact total water head or potential field in Eq. (2) is defined by: $h=Z+p/{\gamma }_{w}$, where Z (m) is elevation above the datum and $p/{\gamma }_{w}$ is pore water pressure, which is normally referred to as uplift pressure force (m) at that point. Pore water pressure on phreatic lines is zero ($p/{\gamma }_{w}=0)$ and hence the potential field is defined by Z-values alone. Below the phreatic line, pore water pressure will be positive. For water flowing through the soil, its pore pressure acts upward against dam foundations. This pore pressure is known as uplift pressure, which exerts forces upward against structure bases. Uplift pressures are modeled by constructing a SEEP/W numerical model.

Numerical simulation

The first step in using numerical simulation is to choose a suitable numerical model for the problem. In this study, SEEP/W software is used for its capability on seepage simulation. Figure 2 shows the largest cross section and the finite elements (FE) meshes for the Sabalan rock fill dam. In Fig. 2, elements of about 10 m grid sizes is shown for clear viewing mesh representation; however, total the number of 70,703 elements (element of 1 m grid size) are used in all the model simulated of optimum element.

Fig. 2

Cross section and finite elements meshing for Sabalan rock fill dam with variable parameters

Sensivity analysis for different mesh sizes demonstrated that the results are independent of mesh size, if at least 60,000 elements are used in the simulations (Fig. 3). According to Fig. 3, when number of elements increases up to 70,703 meshes, percent of relative error (RE %) became less than 0.01%, which is computed on the basis of uplift pressure simulation for different element dimensions.

Fig. 3

Determination of the optimal number of elements in numerical simulation

Details of the Sabalan rock fill dam is presented in Table 1. Dam core in the upstream and downstream faces has three layer of filters.

Table 1 Details of the Sabalan rock fill dam

The specification of boundary condition in numerical model is as below:

The upstream river bed and dam upstream slope was selected with “total head.” The total head (H_upstream) in this dam is normal depth of water behind the dam (h = 43 m) plus height of any point from the arbitrary datum (z). As Fig. 2 shows, the total head is H_upstream = 172 m.

River bed in the downstream is also specified as the total head (H_downstream) and its value is H_downstream = 130 m. The lowest bottom border is impermeable foundation and thus is a boundary with zero discharge (Q = 0). This situation is also valid for the left and right boundaries. Soil permeability values for Sabalan rock fill dam in the numerical simulation are included in Table 2.

Table 2 The permeability of different parts of Sabalan rock fill dam (Ashnab Consulting Engineers 2000)

This study tests numerically variation of uplift pressure, hydraulic gradient and discharge (seepage) from the dam with changes in the clay core thickness and position of cutoff wall in the base of Sabalan earth fill dam. Thus independent variables are: position of cutoff wall in the clay core base (X), the depth of the cutoff wall (d') and the hydraulic conductivity of cutoff wall (k'). Table 3 presents the effective parameters. In Table 3, L is the width of clay core in the foundation level. Figure 4 shows the largest cross section of Sabalan rock fill dam with a cutoff wall in the toe of core position (X/L = 1) with depth of 12.5 m.

Table 3 The range of changes for the effective parameters of Sabalan rock fill dam

Fig. 4

Position of cutoff wall in Sabalan rock fill dam in X/L = 1 and with depth of 12.5 m

Results and discussion

In Fig. 5, iso-pressure curves of the Sabalan rock fill dam are shown. According to Fig. 5, the effect of clay core on reduction of phreatic line (blue color) is clear. The cutoff wall in the foundation of dam also causes a reduction about 20 m in the pressure head.

Fig. 5

Iso-pressure curves of the Sabalan rock fill dam and its foundation by numerical simulation (cutoff depth = 50 m)

For investigation of the hydraulic gradient and seepage from the dam and foundation, the cutoff wall was placed in five different positions according to Table 3. By numerical simulation, hydraulic gradient changes along the clay core width (on the foundation level) is shown in Fig. 6. The hydraulic gradient before the cutoff wall (on the left side) gradually increases up to the cutoff wall. The maximum gradient is at the cutoff wall, and then, it reduces again on the right side of cutoff wall until entering the downstream shell. The hydraulic gradient reaches to the minimum amount at the shell. In addition, the hydraulic gradient is decreasing by transferring in the position of cutoff wall from the heel to the toe of the clay core, and the difference percentage between two hydraulic gradients of the place of cutoff wall in heel and toe of the dam is about 34%. Therefore, the optimal position of the cutoff walls to reduce the hydraulic gradient is at the toe of the dam core.

Fig. 6

Hydraulic gradient changes at different positions of cutoff wall

Figure 7 shows the changes of the seepage (q) provided for different position of cutoff walls (X/L). By more transferring in the position of cutoff wall from the heel to the toe of the dam core, the seepage increases. The difference percentage between two values for seepage is about 0.2% between the left (heel) and right (toe) position of cutoff wall. This reduction in q is negligible. Therefore, it can be concluded that the cutoff position under the core does not affect the discharge of the seepage.

Fig. 7

Changes in seepage in unit length of the dam in various positions of cutoff wall (X/L)

The thickness of the core on the foundation (L) with five different values, and the cutoff wall locations (X/L) in five different points (according to Table 3) is investigated on hydraulic gradient and seepage in Figs. 8 and 9. Based on Fig. 8, when the thickness of the clay core increases, hydraulic gradient decreases. Overall the reduction of hydraulic gradient with X/L in not linear but between X/L = 0.25–0.7, hydraulic gradient remains constant. The values of 0 < X/L < 0.25 are near the upstream dam shell and the values 0.7 < X/L < 1 are near the downstream dam shell. In the 0 < X/L < 0.25 area, water enters from high-permeability medium to the low-permeability medium (dam core) and in the 0.7 < X/L < 1 area, water enters from low-permeability medium (dam core) to the high-permeability medium (dam shell). In these areas, water potential head loss is high and therefore high variation in hydraulic gradient occurs. The lowest hydraulic gradient is for X/L = 1, i.e., cutoff wall in clay core toe position.

Fig. 8

Effect of thickness of the core (on the foundation level) on hydraulic gradient

Fig. 9

Effect of thickness of the core (on the foundation level) on seepage

Based on Fig. 9, seepage decreases when the thickness of the clay core increases. The difference percentage between two values for seepage is about 0.5% between the thicknesses L = 28–46 m. This reduction in q is negligible. Figure 9 shows that the lowest amount of seepage is in position X/L = 0 (at heel of clay core) and the highest amount of seepage is in position X/L = 1. The slope of increasing in seepage from the X/L = 0–0.5 is higher than for X/L = 0.5–1.

Figure 10 shows the effect of changes the thickness of the clay core on uplift pressure. The uplift pressure is increased before the wall (the left side of the wall), and it is decreased after the wall with increasing the cutoff wall. Because of permeability of clay cores is less than the permeability of dam shell, the uplift pressure in the connection place of the shell with the core display a steep slope reduction and the most reduction occurs in this location.

Fig. 10

Effect of thickness of the core (on the foundation level) on uplift pressure

The total variation of the uplift pressure by decreasing the core thickness on the foundation level is shown in Fig. 11. Total uplift pressure decreases when thickness of the core decreases. The difference percentage between two values ​​for total uplift pressure is about 39% between the thicknesses 46–28 m.

Fig. 11

Changes in total pressure with decrease in the thickness of the core

Cutoff wall was located with five different permeability amount and in five different points to investigate the effect of changes in the permeability of the materials on the hydraulic gradient and the amount of the seepage according to the Tables 2 and 3.

Figure 12 shows the effect of permeability of cutoff material in different positions on the maximum hydraulic gradient. By reducing the permeability of cutoff, the maximum hydraulic gradient (the hydraulic gradient in the right side of cutoff) increases. This can be explained that a reduction in permeability soil materials causes compression between potential lines. It means that more potential drops occur in less distance. Therefore, the denominator of the deduction decreases in Eq. 1, and this causes an increase in the hydraulic gradient.

Fig. 12

Effect of permeability of cutoff wall in different positions on the hydraulic gradient

Figure 13 shows the effect of permeability of cutoff wall in different positions on the amount of the seepage within the body and foundation of dam. Figure 13 presents that the seepage increases when the permeability increases within material of cutoff wall. The changes are negligible in the seepage, but the seepage has more increase in the permeability of 1 × 10^–7 m s⁻¹ compared with other models, and also the amount of seepage in the position of cutoff wall is more in the middle compared with other positions when the permeability increases.

Fig. 13

Effect of permeability of cutoff wall in different positions on the seepage from the dam body and its foundation

Effect of cutoff wall depth in various positions on the hydraulic gradient and uplift pressure of the dam body and foundation are shown in Figs. 14, 15 and 16, respectively. By increasing the depth of cutoff wall, the hydraulic gradient increases at the cutoff.

Fig. 14

Effect of depth of cutoff wall in different positions on the maximum hydraulic gradient

Fig. 15

Effect of the depth of cutoff wall on the uplift pressure (X/L = 0.5)

Fig. 16

Changes in total pressure with decrease in the depth of cutoff wall

Figure 15 shows the effect of changes in depth of cutoff wall on uplift pressure below the core. According to Fig. 15, the uplift pressure is increased before the wall (the left side of the wall) and it is decreased after the wall with increasing the cutoff wall.

Figure 16 provides the changes in total uplift pressure with decreasing of the depth of cutoff wall. By the more increase in the depth of cutoff wall, the more decrease in the uplift pressure happens. The difference percentage between two values for total uplift pressure is about 0.77% between the depths of cutoff walls 12–75 m.

Figure 17 shows the changes in the seepage amounts compared with the changes in the depth of the cutoff wall and Fig. 18 provides the changes in the amount of the seepage from the foundation compared with the changes in the depth of the cutoff wall (the location of the cutoff wall is in the X/L = 0.5).

Fig. 17

Relative seepage changes in the dam body and foundation of dam against the relative changes in the depth of the cutoff wall (cutoff is located in the middle of the dam core)

Fig. 18

Relative seepage changes from the foundation of dam against the relative changes in the depth of cutoff wall (cutoff is located in the middle of the dam core)

In Figs. 17 and 18, d is the depth of cutoff wall in the base state (d = 50 m) and d' is the change of the depth in cutoff wall under the core of the dam. In Fig. 17, Q' is the seepage from the both of dam body and its foundation in different locations of cutoff wall and Q is the seepage in the base state as well as in Fig. 18. Also Q'' and Q_i are following the seepage from the foundation solely (not dam body) in different locations of cutoff wall and the seepage from the foundation in the base state of Sabalan rock fill dam, respectively.

The seepage from the foundation has more decrease than the seepage from the dam body and foundation by increasing in the depth of cutoff wall under the core of dam. The difference between the percentages of two seepage values for the shortest cutoff wall and the deepest cutoff wall in the body and foundation of dam is 4.33% and 49.31%, respectively (Table 4). Therefore, it can be concluded that the changes of the depth in cutoff wall affect more on the seepage from the foundation.

Table 4 Relative seepage changes in the dam body and foundation of dam against the relative changes in the depth of the cutoff wall of Sabalan rock fill dam

Comparing the results of numerical models to simulate the effect of the depth in cutoff wall on the seepage with SEEP/W model shows that the numerical results of this study, and the results of numerical modeling of Asadi Sakhmarsy et al. (2014) with a study of the effect of cutoff wall on the seepage in Karkheh earth dam have almost the same trends. The seepage is reduced by increasing the depth of the cutoff wall and reducing in permeability according to Fig. 19. As well as other common results of these two studies are the compliance of two amounts of the seepage in the permeability of 1 × 10^–9 and 1 × 10^–10 m³ s⁻¹.

Fig. 19

Effect of depth in cutoff wall in different permeability amounts on the relative seepage from the dam body and foundation of Karkheh dam (black lines) and Sabalan dam (curved dashes)

Table 5 provides the summary of the studied cases for different dam configurations. These configurations are based on: (1) cutoff position, (2) core thickness and (3) cutoff depth. Although for configurations of core thickness and cutoff depth, more than three cases were studied, but for easy comparison, only three cases are provided in Table 5.

Table 5 Summary of the studied cases for different dam configurations

Based on Table 5, each scenario has its own advantage or disadvantage. This study refers to the seepage, hydraulic gradient and uplift pressure under the earth dam, and results show that there is not excellent case, absolutely preferable for design. For example, when the cutoff position is in the center of the clay core, all the three cases of the seepage, hydraulic gradient and uplift pressure are in medium condition, but when the cutoff position is in the heel (upstream) of the clay core, seepage and uplift pressure are low, but hydraulic gradient is high. When the cutoff position is in the toe (downstream) of the clay core, seepage and uplift pressure are high, but hydraulic gradient is low. In addition, this study does not consider the effect of construction costs. For example, it is clear that the deeper cutoff is better respect to low seepage and low uplift pressure, but the deeper cutoff needs more financial support. The presented charts in this study are valid for Sabalan dam, thus for another dam, engineer designer should prepare specific charts with combination of economic charts for optimum design.

Conclusions

The focus of the present study is on the Sabalan (Savalan) rock fill dam in Iran. This study tends to investigate the effect of the thickness of clay core and the depth, thickness and the permeability of the cutoff wall in different positions (from heel to toe of the clay core) on the hydraulic performance of the dam. The dependent parameters are uplift pressure (U), hydraulic gradient (i) and seepage (Q), and these factors were investigated using SEEP/W software. SEEP/W is based on finite-element method (FEM). Sabalan (Savalan) rock fill dam is now at safe operation, and this study wants to find optimum design with comprising U, i and Q. All changes in dam layout that create reduction in U, i and Q would be preferable. For this purpose, dimensionless variables were used to create suitable charts. Generation of these charts require several numerical models from the dam using independent variables combination. Independent variables include: d’, that is the depth of cutoff wall and is from 12.5–75 m; L’ that is the thickness of the clay core on foundation and varies from 28–46 m; k′ that is permeability of the cutoff wall and differs from 1 × 10^–10–1 × 10^–7 m/s and X that is cutoff location in base of the clay core and differs from 28–46 m. According to the numerical simulations, the main results are summarized as follows:

The more movement of the cutoff wall from the heel (X = 0 m) to the toe of the core of dam (X = 46 m), results the more seepage from the both dam body and dam foundation and also the less hydraulic gradient. In fact, cutoff location for X = 0 m creates proper condition respect to lower seepage, but produces unsuitable condition respect to high hydraulic gradient. Hydraulic gradient controls piping (soil particles movement), thus high hydraulic gradient is not proper for foundation materials. Installation of filter material around the clay core can reduce soil particles movement. Probably it is the reason that most of the dam designers prefer to locate the cutoff walls in the center of the clay core at dam foundations.

By reducing the permeability of the material of the cutoff, seepage decreases, but hydraulic gradient increases. This result shows that zero permeability of the cutoff wall does not produce proper condition with respect to the hydraulic gradient. Suitable permeability of the cutoff wall should be selected so that to control seepage and in the same time set up hydraulic gradient at the low amount.

With increasing the cutoff wall depth, the uplift pressure is increased before the cutoff wall (the left side of the cutoff wall), and it is decreased after the cutoff wall. But the resultant of the uplift pressure (Fig. 16) is lower for deep cutoff (d = 75 m) than shallow cutoff wall (d = 12.5 m).

The seepage through the solely foundation has more decrease than the seepage through the both dam body and foundation of dam and the hydraulic gradient increases with increasing of the depth of cutoff wall. This shows more effect of cutoff wall in foundation than dam body, and this is obvious. Seepage in dam body is controlled with semi-impervious clay core and seepage in dam foundation is controlled with cutoff wall.

The discharge through the dam body and foundation of dam slightly was reduced with increasing the thickness of cutoff wall. Thus minimum thickness of the cutoff wall is sufficient to control seepage.

The more thickness of the clay core results in the less hydraulic gradient and the less discharge of the seepage, but yields the more uplift pressure. On the other hand, more thickness of the clay core has less shear strength, and this phenomenon reduces slope stability of the dam. The latter is not the topic of the present study and may suggest for the future studies.