Introduction

Flow structure is affected by the shear stress distribution in open channels. The flow resistance and characteristics of sediment and deposition are influenced by the bed and wall shear stresses. These shear stresses play important role in the determination of the values of average shear force carried by walls (%SFw). Although experimental studies are widely adopted to measure the shear stress, the exhaustive and laborious procedures of experimental work prompted different approaches such as numerical, analytical and semianalytical methods used to calculate the shear stress distribution (Bonakdari et al. 2015; Hosseini et al. 2019; Sheikh Khozani and Bonakdari 2016; Sterling and Knight 2002; Yang et al. 2012). These new methods are cost efficient and eliminate the difficulties, in particular reducing the errors of experimental works. Using a new method based on the entropy approach and presenting equations for calculating shear stress distribution in open channels with different cross sections of circular and rectangular were investigated (Bonakdari et al. 2015; Sheikh Khozani and Bonakdari 2018; Sheikh and Bonakdari 2016). Numerous researches used the soft computing methods to predict different phenomena in the hydrology and hydraulic fields (Azamathulla and Zahiri 2012; Bonakdari et al. 2018; Sheikh Khozani et al. 2017, 2018, 2019). Sheikh Khozani et al. (2016a, b) estimated %SFw in the smooth and rough boundaries using genetic algorithm artificial (GAA) neural network and genetic programming (GP). Not only the genetic-based modeling technique, the support vector machine (SVM) has also been receiving attention in modeling the reference evapotranspiration (Sheikh Khozani and Bonakdari 2018), stage–discharge relation including the hysteresis effect (Sheikh Khozani et al. 2018), suspended sediment (Yilmaz et al. 2018) and shear stress estimation in circular channels (Sheikh Khozani et al. 2017). Utilizing the advantages of SVR that are not depending on the dimensionality input space for complex computations and excellent generalization capability with high prediction accuracy, this research attempts to investigate the performance of SVR in modeling the percentage of shear force in channels with rough boundaries.

The aim of this paper is to minimize errors in estimating the shear stress distribution. As such, the designing process of more stable channels is permissible by having a more accurate prediction of %SFw. To achieve this goal, the SVR model is extended and the effective parameters of %SFw are determined. To find the most effective parameters, varying input combinations were considered and investigated. Since the kernel functions are very important in the performance of SVR model, different kernel functions were studied and the best kernel function in estimating %SFw is selected. Finally, the performance of the most appropriate SVR model prediction was assessed based on three different regression equations which proposed by Knight (1981), Knight et al. (1984) and Knight et al. (1994).

Materials and method

Data used

The data measured by Knight (1981) in rough rectangular channels were used in order to predict the %SFw using the SVR model. The experiments were conducted in a flume with 15 m long, 460 mm wide, on a constant bed slope of 9.58 × 10−4. The wall and bed shear force were measured using the Preston tube technique, whereby the %SFw was measured at different flow depths. Based on the data, Knight then extracted nonlinear regression formula for calculating the %SFw as an exponential function as:

$$ \% {\text{SF}}_{\text{w}} = e^{\alpha } \left( {\tanh \left( {\pi \beta } \right) - 0.5\left[ {\tanh \left( {\pi \beta } \right) - \beta } \right]^{2} } \right) $$
(1)

where the relationships of α and β are

$$ \alpha = - 3.264\log \left( {\frac{B}{h} + 3} \right) + 6.211 $$
(1.1)
$$ \beta = 1 - \log \left( {\frac{{k_{sb} }}{{k_{sw} }}} \right)/5 $$
(1.2)

where ksb and ksw are the bed and wall roughness, respectively. Knight et al. (1984) analyzed their own data including the data in Knight (1981) and plotted onto a log–log scale. By assuming a simple relationship between %SFw and B/h, they derived the following equation

$$ \log (\% {\text{SF}}_{\text{w}} ) = - 1.4026\log \left( {\frac{B}{h} + 3} \right) + 2.6692 $$
(2)

Equation (2) can be rewritten in another form as

$$ \% {\text{SF}}_{\text{w}} = e^{\alpha } $$
(2.1)
$$ \alpha = - 3.230\log \left( {\frac{B}{h} + 3} \right) + 6.146 $$
(2.3)

Knight et al. (1994) presented another regression equation with a relative wetted perimeter factor as

$$ \% {\text{SF}}_{\text{w}} = C_{sf} e^{\alpha } $$
(3)
$$ \alpha = - 3.23\log \left( {\frac{{P_{b} }}{{C_{2} P_{w} }} + 1} \right) + 4.6052, $$
(3.1)
$$ C_{2} = 1.38 $$
(3.2)
$$ C_{sf} = 1.0\quad {\text{for}}\;\frac{{P_{b} }}{{P_{w} }} < 4.374 $$
(3.3)
$$ C_{sf} = 0.6603\left( {\frac{{P_{b} }}{{P_{w} }}} \right)^{0.28125} \;\;{\text{for}}\;{\text{else}} $$
(3.4)

These are some parameters in shear stress that affects the percentage of shear force (%SFw) such as the geometry of the channel (b), flow depth (h), bed and wall roughness (ksb, ksw), energy slope (Sf), flow velocity (V), fluid density (\( \rho \)), gravitational acceleration (g) and hydraulic radius (R). Thus, %SFw can be considered as a function of

$$ \% {\text{SF}}_{\text{w}} = F\left( {\rho ,g,B,h,k_{sb} ,k_{sw} ,R,S_{f} ,V} \right). $$
(4)

Using the Buckingham’s theorem, the dimensionless parameters influencing %SFw can be written as

$$ \% {\text{SF}}_{\text{w}} = f\left( {\frac{B}{h},{\text{Fr}},\frac{{k_{sb} }}{{k_{sw} }},{\text{Re}}} \right), $$
(5)

where \( \frac{B}{h} \) is the aspect ratio, \( {\text{Fr}} \) is the Froude number, \( \frac{{k_{sb} }}{{k_{sw} }} \) is the relative roughness and Re is the Reynolds number.

Support vector machines

The support vector machine (SVM) method (Vapnik 2000) is one of the most common machine learning methods used for various classification and simulation problems. The simulation branch of SVM that is applied to regression problems is known as support vector regression (SVR). SVR is used to find a relation between the input variables of \( X = \left\{ {\overrightarrow {{x_{1} }} ,\;\overrightarrow {{x_{2} }} , \ldots ,\;\overrightarrow {{x_{n} }} } \right\} \) and the observed variables of \( T = \{ t_{1} ,\;t_{2} , \ldots ,\;t_{n} \} \). Therefore, SVR can predict the output vector of \( O = \{ o_{1} ,\;o_{2} , \ldots ,\;o_{n} \} \) by using the input variables. When O is closer to T, the SVR model has higher performance. The inputs of this study are \( \frac{B}{h},{\text{Fr}},\frac{{k_{sb} }}{{k_{sw} }},{\text{Re}} \), and the output is the %SFw. The linear regression that predicts the output using the inputs is defined as

$$ y_{i} = w_{i}^{T} x_{i} + b, $$
(6)

where w represents the weight vectors and b is the bias. In the SVR method, the model is penalized when the errors exceed a defined constant, denoted as epsilon (ε). Penalization is done by the loss function defined as

$$ L_{\varepsilon } (t_{i} ,y_{i} ) = \left\{ {\begin{array}{*{20}c} 0 & {\left| {t_{i} - y_{i} } \right| \le \varepsilon } \\ {\zeta_{i} } & {\left| {t_{i} - y_{i} } \right| > \varepsilon } \\ \end{array} } \right., $$
(7)

where ζi is a nonnegative slag variable, ti is the observed output and yi is the output of the regression process. In this equation, the loss function is equal to zero if the difference between the regression and observed outputs is less than ε. Otherwise, the loss function takes amount. By using Eq. (7), it can be concluded that \( - \varepsilon - \zeta_{i}^{ - } \le t_{i} - y_{i} \le + \varepsilon + \zeta_{i}^{ + } \) must be correct. With this equation, the new shape of the loss function could be written as

$$ L_{\varepsilon } (t_{i} ,y_{i} ) = \zeta_{i}^{ - } + \zeta_{i}^{ + } . $$
(8)

The SVR process attempts to find the optimum regression function that minimizes the loss function. Therefore, if the empirical risk (Remp) is minimized, then the most accurate regression is obtained. The Remp is defined as

$$ R_{\text{emp}} \left[ {y_{i} } \right] = \frac{1}{n}\sum\limits_{i = 1}^{n} {L_{\varepsilon } } (t_{i} ,y_{i} ), $$
(9)

where yi is the output of the regression model and n is the number of considered samples. However, in the process of finding the minimum value of Remp, there is a probability that the size of the model would increase undesirably. Therefore, the complexity term should be added to Eq. (9) to minimize the issue. The regularized risk function (Rreg) [Eq. (10)] is defined as the summation of Remp and the norm of w, ||w||. Minimizing Rreg is a two-objective minimization which finds the most accurate regression with the smallest model size.

$$ R_{\text{reg}} \left[ {y_{i} } \right] = R_{\text{emp}} \left[ {y_{i} } \right] + \frac{1}{2}w^{T} w. $$
(10)

The standard form of Rreg (Çimen 2008; Smola 1996) is obtained by using Eqs. (8) and (10) as

$$ R_{\text{reg}} \left[ {y_{i} } \right] = C\sum\limits_{i = 1}^{n} {(\zeta_{i}^{ - } + \zeta_{i}^{ + } )} + \frac{1}{2}w^{T} w, $$
(11)
$$ {\text{such}}\;{\text{that}}\;\left\{ {\begin{array}{*{20}c} { - t_{i} + y_{i} + \varepsilon + \zeta_{i}^{ + } \ge 0} \\ {t_{i} - y_{i} + \varepsilon + \zeta_{i}^{ - } \ge 0} \\ {\zeta_{i}^{ - } \;{\text{and}}\;\zeta_{i}^{ + } \ge 0} \\ \end{array} } \right., $$
(12)

where C is a positive constant that serves as a trade-off parameter to determine the degree of Remp.

The following linear regression equation is obtained from the minimization process of Eqs. (11) and (12),

$$ {\text{for}}\;S = \left\{ {i\left| {0 < \alpha_{i}^{ + } + \alpha_{i}^{ - } } \right. < C} \right\} \cdots y_{j} = \sum\limits_{i = 1}^{\left| S \right|} {(\alpha_{i}^{ + } + \alpha_{i}^{ - } )} x_{i} x_{j} , $$
(13)

where S is the set of support vectors and \( \alpha_{i}^{ + } \) and \( \alpha_{i}^{ - } \) are the Lagrange multipliers.

Kernel functions are employed to transfer the linear regression function into a nonlinear one. Therefore, the kernel function is added to Eq. (13) as

$$ y_{j} = \sum\limits_{i = 1}^{\left| S \right|} {(\alpha_{i}^{ + } + \alpha_{i}^{ - } )} \,K(x_{i} ,x_{j} ), $$
(14)

where K(xi,xj) represents the investigated kernel function. Selecting the appropriate kernel function directly affects SVR model performance. Nonetheless, there is no definitive rule to define kernel functions. Therefore, eight different kernel functions were employed in this study and their individual performance was compared. Details of the considered kernel functions are presented in Table 1.

Table 1 Used kernel function equations
Full size table

The optimum selection of the C and ε constants has a significant effect on SVR model performance. According to Table 1, despite the linear kernel function, other kernel functions have another constant that must be determined. Therefore, the results of each SVR model with the second to eight kernel functions are needed to determine the three parameters of C, ε and the kernel constant. In this study, these parameters are determined via trial-and-error method. In the trial-and-error approach, some loops are added to the main SVR program. Each constant was changed in 20 stages; therefore, for each kernel function, nearly 8000 (that is 20 × 20 × 20) runs were performed.

Results

Goodness fit of model

Three statistical evaluation criteria were used in this study to assess the model performance, i.e., root-mean-square error (RMSE), mean absolute error (MAE) and average absolute deviation (%δ). The RMSE measures the goodness of relevant fitted to %SFw values, and MAE yields a more balanced perspective of the goodness of fit at moderate prediction values. The %δ is a parameter that compares the error between experimental data and the SVR model results. These statistical parameters were utilized to identify the accuracy of different soft computing methods (Sheikh Khozani et al. 2016, 2017). The selected statistical parameters are defined as:

$$ {\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {x_{ip} - x_{im} } \right|} , $$
(15)
$$ {\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {x_{ip} - x_{im} } \right)^{2} } }}{n},} $$
(16)
$$ \delta = \frac{{\sum\limits_{i = 1}^{n} {\left| {x_{ip} - x_{im} } \right|} }}{{\sum\limits_{i = 1}^{n} {x_{ip} } }} \times 100, $$
(17)

where xim and xip are the measured and predicted values of %SFw, respectively.

Selection of the most appropriate kernel function

There is the possibility of using a nonlinear function in the input space for changing to a linear function in the characteristics space if we can select an appropriate kernel function. Selecting the most appropriate kernel function was investigated through eight standard conversions of kernel functions that are most used. In modeling using SVR, four non-dimensional parameters of B/h, Fr, Re and kb/kw were used as inputs. As shown in Table 2, the exponential kernel function (RMSE = 0.0916, MAE = 0.0772 and %δ = 14.9238) is the most appropriate kernel, and the Laplacian functions with RMSE of 0.0925 showed good results in predicting %SFw after the exponential function. The multiquadratic kernel function predicts the worst %SFw with the highest error values obtained, i.e., RMSE = 0.3189, MAE = 0.2613 and %δ = 65.0621.

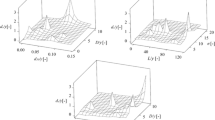
Table 2 Selection of the more appropriate kernel function
Full size table

Figure 1 shows the results of different kernel functions for testing and training datasets as scatter plots. The trend line for the testing data is illustrated in Fig. 1. The coefficient of determination (R2) value shows how well the data fit the experimental results. The exponential kernel function with R2 of 0.9547 shows the highest adaption of predicted %SFw on its experimental value. For the test dataset, nearly all kernel functions predicted underestimated values for %SFw. The sigmoid and multiquadratic kernel functions predict the least convincing results with R2 of 0.7705 and 9 × 10−8, respectively. Obviously, when the multiquadratic kernel function was used, the model predicted a constant value of 0.4016 for %SFw for all different aspect ratios. The straight line obtained for the trend line indicates that this model could not predict reasonable values for %SFw. Therefore, the exponential kernel function was selected as the more accurate Kernel function in the following step.

Fig. 1
figure 1

Scatter plot of the SVR model with different kernel functions

Full size image

Selection of the most appropriate input combination

In this step, the parameters with less impact on the modeling output and increased the model complication are recognized and omitted from the model. The most important stage in the construction process of intelligent modeling is selecting the most appropriate input combination. To identify the most important parameters in modeling with SVR, eight different input combinations were studied to find the most important parameters in estimating the values of %SFw. Some of input combinations contain two variables since with increasing number of input variables; few soft computing methods can handle the modeling procedure. These input combinations are shown in Table 3.

Table 3 The variables of each input combination
Full size table

Table 4 presents the results of the comparison between these input combinations. Input combination (ii) produced the lowest values of statistical parameters, with RMSE = 0.087, MAE = 0.0674 and %δ = 12.6250. By ignoring the Re number, the model does not present accurate results and the error values evidently increased when this parameter was omitted. Input combination (viii), by ignoring the aspect ratio and Re, produced the worst predicted values with RMSE = 0.3181, MAE = 0.256 and %δ = 64.5425. Therefore, the Re and aspect ratio are the most influential parameters on estimating accurate shear force percentage values.

Table 4 Statistical parameters for selection of the more appropriate input combination
Full size table

The results of selecting the most appropriate input function are illustrated in Fig. 2 as a scatter plot. The trend line for the dataset is also plotted in this figure to provide visualization on the prediction ability. Input combinations (ii) and (v) showed closer results to the fitted line while the equations of their trend lines indicate the goodness fit of these input combinations. The results of input combination (v) are better than input combination (ii). This is due to the omission of aspect ratio parameter in the input combination (v), which it plays an effective role in values of %SFw, and then, the input combination (ii) was selected as the most appropriate input combination. For input combination (viii), with omitting the influence of the aspect ratio and Re, the model could not estimate accurate results especially for testing data and this is supported by R2 of 0.0926. Also, by ignoring the Re values as an input parameter in modeling procedure, the model did not show a good performance in estimating the percentage of shear force carried by walls either.

Fig. 2
figure 2

SVR model with various input combinations for test data

Full size image

The output of the best SVR model is presented in Fig. 3 as a program for estimating the %SFw. This program was prepared in MATLAB software, and the exponential kernel function and input combination (ii) were used in the structure of this program. This program is simple, which is rarely seen in modeling with the SVR method. In this program, the three inputs in input combination (ii) consist of B/h, Fr and Re and were taken from the user. After using the exponential kernel function in calculations, the %SFw was obtained.

Fig. 3
figure 3

Output of the more appropriate SVR model

Full size image

Comparison between the proposed model and regression equations

The SVR model was compared with some regression equations in predicting the percentage of shear force carried by walls. In modeling with the most appropriate SVR model, the exponential kernel function was used with input combination (ii). Table 4 presents the results of this comparison. The SVR model with RMSE of 0.0565 performed the best compared to the regression equations obtained by other equations which proposed by researchers in this study. Knight’s (1981) equation presented for rough boundaries had good results with RMSE of 0.0641. On contrary, the other two equations which presented for smooth rectangular channels, shown in Table 5, did not have accurate results even with the highest values of statistical parameters. Since the equations presented by Knight (1981) showed the worst results of predicting %SFw, then it can be deduced that the roughness parameter has high influence on predicting %SFw. On the other hand, although the roughness ratio was omitted in input combination (ii), this model still could predict an accurate result for %SFw.

Table 5 Statistical parameters of comparison between SVR and other equations
Full size table

The results of testing are illustrated in Fig. 4 as scatter plots and hydrographs for the entire dataset. The figure shows a good agreement between the observed and predicted SVR model values. Moreover, the predicted %SFw values were close to the measured values; the results were closer to the line of agreement in the scatter plot than the other equations. The trend line for the SVR model and each equation is shown in scatter plots, where the gray straight line is for the SVR model and the black dash line represents other models. Interestingly, only the equation of Knight (1981) was able to estimate a more close prediction values, and other equations were not able to accurately predict %SFw values. The performance of Eq. (2) is good for the data between the ranges of 1–20, but for the other data, the model overestimated predicted values for %SFw. As seen in Fig. 4, the values of %SFw which calculated using Eq. (3) provide similar findings with Eq. (2) and present low performance for estimating %SFw. The hydrographs show the residual of experimental data and data predicted by the models. Evidently, the SVR model graph has lower deviation from the straight line, but the other equations which presented for smooth channels [especially Eqs. (2) and (3)] demonstrated higher deviation from the straight line.

Fig. 4
figure 4

Comparison between SVR model and other equations in predicting the %SFw for the entire dataset

Full size image

Conclusion

The SVR model was used to predict %SFw in a rectangular channel with non-homogeneous boundary roughness. The SVR model was extended in two phases. The best kernel function was selected after investigating eight different kernel functions, whereby the exponential kernel function was found to be the most appropriate. To study the amount of influence of different parameters on the %SFw values, four parameters were assumed and eight input combinations were selected for this purpose. The results showed that the influence of aspect ratio and relative roughness is higher in predicting the %SFw. Input combination (ii) containing B/h, Fr and Re was selected as the best input combination. Although the relative roughness was not included in the input combination (ii), the proposed model was able to present accurate results in predicting %SFw. A simple MATLAB code was presented as the output of the more appropriate SVR model. Finally, the best SVR model was compared with three equations presented by other researchers. It can be deducted that the equation for rough rectangular channels presented by Knight (1981) demonstrated good results of prediction of %SFw, but the SVR model with RMSE of 0.0565 performed better than Knight’s equation with RMSE of 0.0641. The equations for smooth channels derived by Knight et al. (1984) and Knight et al. (1994) showed the worst results for predicting %SFw with RMSE of 0.2413 and 0.4048, respectively. The smooth channel equations overestimated the values for %SFw in channels with rough boundaries. As such, these equations are not applicable for predicting %SFw in these channels. The SVR presents a high-performance model in predicting the hydraulic parameter of %SFw in rectangular channels with rough boundaries.