Introduction

Expansion of industrial activities over the past few decades has contributed to increased levels of metallic constituents in the aquatic environment (Qaiser et al. 2009). Bivalent metal ions, such as Cu(II), Ni(II) and Cd(II), and their compounds commonly found in industrial wastewater would accumulate in fish and other aquatic organisms. These metal ions are transferred to higher animals through food chain by bioaccumulation, bioconcentration and biomagnification (Hossain et al. 2014).

The presence of excess Ni(II) ions in the environment, particularly in water, would cause various types of acute and chronic disorders, such as damage to lungs and kidneys, gastrointestinal distress, pulmonary fibrosis and skin dermatitis (Borba et al. 2006). Therefore, removal of Ni(II) from industrial wastewater is a necessity to safeguard the quality of life in the ecosystem. In this regard, various techniques are applied for the treatment of heavy metals, including chemical precipitation, coagulation/flocculation, ion exchange, electrochemical processes and membrane technology (Amuda and Ibrahim 2006).

Chemical methods are found to be neither economical nor environmentally friendly, as compared to biosorption processes (Ali 2013). On the other hand, plant-based materials, such as orange peel (Feng et al. 2011), peanut shell (Krowiak et al. 2011), Cassia fistula biomass (Hanif et al. 2007), Ficus religiosa leaves (Qaiser et al. 2009), Artocarpus camansi Blanco (breadnut) (Lim et al. 2016), Artocarpus altilis (Lim et al. 2015), dragon fruit skin (Priyantha et al. 2013) and Artocarpus odoratissimus (Tarap) (Lim et al. 2013), have shown remarkable biosorption abilities. In addition to being effective and economical for treatment of wastewater having low heavy metal ion concentrations, regeneration would not be necessary for biosorption due to ready availability of such materials.

Biosorption of metal ions can help to design kinetic models and to select the optimum operating conditions in full-scale batch process. The kinetic behavior of metal ion can be investigated using pseudo-first-order and pseudo-second-order models, as mentioned below (Rashid et al. 2016),

$$\log \left( {q_{\text{e}} - q_{\text{t}} } \right) = - \frac{{k_{1} }}{2.303}t + \log \left( {q_{\text{e}} } \right)$$
(1)

where qe and qt are the sorption capacity (mg kg−1) at equilibrium and at time t, and k1 is the rate constant of pseudo-first-order sorption (min−1).

$$\frac{t}{{q_{\text{t}} }} = \frac{1}{{q_{\text{e}} }}t + \frac{1}{{k^{\prime}q_{\text{e}}^{2} }}$$
(2)

where k′ is the rate constant of pseudo-second-order sorption (kg mg−1 min−1).

Adsorption equilibrium data describe the relationship between the mass of adsorbate adsorbed per unit mass of adsorbent, and adsorption isotherms represent the liquid-phase equilibrium concentration of adsorbates (Belhachemi and Addoun 2011). Two-parameter adsorption models (Langmuir, Tempkin and Freundlich) and three-parameter adsorption models (Redlich–Peterson and Sips) are the most common models which provide valuable data for designing adsorption systems (Tosun 2012). A commonly used linearized Langmuir isotherm relationship is given by (Shahmohammadi-Kalalagh and Babazadeh 2014),

$$\frac{{C_{\text{e}} }}{{q_{\text{e}} }} = \frac{1}{{q_{{\max} } b}} + \frac{{C_{\text{e}} }}{{q_{{\max} } }}$$
(3)

where qmax is the maximum monolayer capacity of biosorbent (mg kg−1), b is the isotherm constant (L mg−1), Ce is the equilibrium concentration of adsorbate (mg L−1) and qe is the mass adsorbed per unit mass of adsorbent (mg kg−1).

The linearized Freundlich equation is expressed as (Olalekan et al. 2013),

$$\ln q_{\text{e}} = \ln k_{\text{f}} + \frac{1}{n}\ln C_{\text{e}}$$
(4)

where kf is the Freundlich constant (mg kg−1) and n is adsorption intensity.

The Thomas model has been derived using the assumptions of Langmuir kinetics of adsorption–desorption and no axial dispersion. It obeys the second-order reversible reaction kinetics (Tamilselvi and Asaithambi 2015). The Thomas model is given as (Chu 2010),

$$\ln \left( {\frac{{C_{\text{o}} }}{{C_{\text{t}} }} - 1} \right) = \frac{{k_{\text{Th}} q_{\text{o }} w}}{v} - k_{\text{Th}} C_{\text{o}} t$$
(5)

where kTh is the Thomas rate constant (mL min−1 mg−1), Co and Ct are the inlet and outlet adsorbate concentrations (mg L−1), qo is the sorption capacity of the adsorbent per unit mass of the adsorbent (mg g−1), w is the mass of adsorbent (g), v is the flow rate (mL min−1) and t is the time of measurement (min).

The Adams–Bohart model is applied to sorption data in order to describe the breakthrough curve. This model is used for the description of the initial part of the breakthrough curve (Salamatinia et al. 2008). It is given as (Baral et al. 2009),

$$\ln \frac{{C_{\text{t}} }}{{C_{\text{o}} }} = k_{\text{AB}} C_{\text{o}} t - k_{\text{AB}} N_{\text{o}} \frac{Z}{F}$$
(6)

where kAB is the mass transfer coefficient (L mg−1 min−1), No is the saturation concentration (mg L−1), Z is the bed height (cm) and F is the linear flow rate (cm min−1).

The Yoon–Nelson model is derived based on the assumption that the rate of decrease in the probability of adsorption for each adsorbate molecule is proportional to the probability of adsorption of adsorbate and the probability of adsorbate breakthrough on the adsorbent (Ayoob and Gupta 2007). It is given as (Aziz et al. 2014),

$$\ln \frac{{C_{0} }}{{C_{0} - C_{\text{t}} }} = k_{\text{YN}} t - \tau k_{\text{YN}}$$
(7)

where kYN is the rate constant (min−1) and τ is the time required for 50% adsorbate breakthrough (min).

Cellulose, hemicellulose and lignin are structural organic substances present in plant-based materials (McKendry 2002). These substances comprise many functional groups, such as carbonyl, phenolic, carboxyl, alcohol and ester (Sud et al. 2008). Plant-based materials therefore show a strong affinity to biosorb heavy metals. The swelling effect of particles can happen by adsorption of large amount of water, thereby increasing the volume-to-area ratio, which eventually enhances the biosorption process (Demirbas 2008). Breadfruit plants (Artocarpus species) are rich in phenolic compounds including flavonoids, stilbenoids and arylbenzofurons (Abu Bakar et al. 2009; Jagtap and Bapat 2010). The formation of negative ions by losing H+ from the hydroxyl group of phenols helps to attract cations (Al-Asheh et al. 2000). The present study was carried out using the fruit peel of Artocarpus nobilis, which is a waste material. Artocarpus nobilis plant, a variety of breadfruit, is endemic to Sri Lanka and restricted to lowland rain forests. The objective of this research is to investigate the ability of the peel of the fruit of Artocarpus nobilis for biosorption of Ni(II) from synthetic solutions through the application of static and dynamic adsorption models, and to investigate the suitability of using this low-cost adsorbent for the removal of Ni(II) from contaminated solutions.

Materials and methods

Materials

The peel of Artocarpus nobilis fruits was removed, air-dried and stored until biosorption experiments were conducted. Resulting dried samples were blended and sieved to obtain particle sizes in the range of 0.710 mm < d < 1.0 mm. The stock solutions of Ni(II) were prepared using analytical grade NiSO4 dissolved in deionized water. Solution pH was adjusted as needed using analytical grade NaOH and/or HNO3.

Characterization of biosorbent

Air-dried fruit peel of Artocarpus nobilis was crushed into fine powder and mixed with dried KBr in a ratio of 1:100, and Fourier transform infrared (FTIR) spectra were recorded for the pellets prepared.

Unprocessed peel (1.25 g) was stirred with 0.25 L of 0.10 mol L−1 NaNO3 solution. The pH of the peel suspension was adjusted to 4.0 by adding HNO3 acid (0.138 mol L−1, as standardized with primary standard Na2CO3 solution of 0.100 mol L−1). Then, the pH was raised up to 10.0 by adding small volumes of NaOH solution of 0.0990 mol L−1 as standardized with the secondary standard HNO3 acid solution, and the pH after each addition was recorded. This experiment was repeated for 0.010 mol L−1 and 0.0010 mol L−1 NaNO3 solutions. Thereafter, the surface charge density was calculated and plotted against pH of the solution in order to determine the point of zero charge.

Optimization of experimental parameters

A series of solutions containing 0.100 g of each peel and 50.0 mL of 10.0 mg L−1 Ni(II) solution was shaken at a speed of 150 rpm. Remaining Ni(II) concentration in each solution was determined immediately, using Spectro-Electronic M Series atomic absorption spectrophotometer (AAS) at ambient temperature of 27 ± 1°C. These solutions were shaken for the optimum time period. Thereafter, each solution was allowed to stand for different settling times, and the remaining Ni(II) content was determined.

The same solutions [50.0 mL of 10.0 mg L−1 Ni(II) solution with 0.100 g peel] were used to optimize the time period of thermal treatment of the biosorbent at a constant temperature of 125 °C in an oven, and the remaining Ni(II) concentrations were determined. Then, the treatment temperature was optimized using the optimized treatment time at different temperatures using the same oven under other optimized conditions.

The effect of pH on the extent of removal of Ni(II) was determined at different initial solution pH values maintained using 0.1 mol L−1 NaOH and conc. HNO3.

All experiments were performed in triplicate, and average values were reported.

Adsorption isotherms

Amount of biosorption of Ni(II) by peel was determined in each solution (50.0 mL solution with 0.100 g peel) of concentrations changing from 10.0 to 1000.0 mg L−1. The relationship between the extent of biosorption and equilibrium concentration of Ni(II) was studied in order to check the validity of adsorption isotherm models, such as Langmuir and Freundlich.

Adsorption kinetics

The extent of removal of Ni(II) by 2.000 g of fruit peels at different contact times was investigated using 1.0 L of 10.0 mg L−1 of Ni(II) ion solution until equilibrium was reached. Results were analyzed to check the validity of different kinetics models.

Dynamic experiments

Pyrex glass tubes of 1.0 cm internal diameter packed up to a constant bed height of 10.0 cm were used to investigate dynamic biosorption of Ni(II) on the biosorbent. Synthetic Ni(II) solution of 10.0 mg L−1 was fed to the column filled with the biosorbent, and eluent samples were collected at different flow rates at 5-min time intervals. The remaining Ni(II) concentrations were determined for the optimization of flow rate. Then, bed height was optimized in the same manner by changing different packing bed heights from 2.5 to 10.0 cm. In addition, the mass of 3.0 g is sufficient to fill the bed height of 10.0 cm.

Results and discussion

Characterization of the adsorbent

The FTIR spectrum of raw peel, given in Fig. 1, shows sharp and broad absorption peaks representing the functional groups listed in Table 1. The bands at 1243, 1733 and 2850 cm−1 indicate the presence of carboxylic acid derivatives which are very important for complexation with heavy metal ions. The presence of similar bands has been reported for many natural adsorbents, such as breadfruit peel, mango peel and banana peel (Lim et al. 2015; Iqbal et al. 2009; Castro et al. 2011).

Fig. 1
figure 1

FTIR spectrum of Artocarpus nobilis fruit peel

Full size image
Table 1 Active functional groups present in the peel of Artocarpus nobilis fruit
Full size table

Zero point charge of adsorbent

Surface charge of the peel of Artocarpus nobilis fruit is negative, which becomes more negative as the medium pH increases according to the surface charge determined as a function of pH for different ionic strengths, as shown in Fig. 2. The point of zero charge is estimated in the pH range of 3.0–4.5 based on the variation of the surface charge with pH. The background electrolyte, NaNO3, is commonly used for surface titrations, as its constituent ions do not specifically bind to the biosorbent surface. Hence, it is assumed that no ion other than protons in the medium binds to the biosorbent during surface titrations. As the natural pH of the Artocarpus nobilis fruit peel is 5.9, adsorption occurs favorably under ambient conditions.

Fig. 2
figure 2

Surface titration curve of the peel of Artocarpus nobilis fruit suspension, plotted as variation of surface charge with pH controlled by additions of NaOH at ambient temperature in NaNO3 solutions of different concentrations. 0.1 M (solid line) 0.01 M (dotted line) 0.001 M (dashed line)

Full size image

Optimization of experimental parameters

The extent of removal of Ni(II), determined using 10.0 mg L−1 solution at zero settling time, was increased within the first 100 min of shaking and then becomes constant. Therefore, the optimum shaking time of interaction of Ni(II) with the peel of Artocarpus nobilis fruit was considered as 120 min, at which 45% removal was obtained. The optimum contact time for removal of Ni(II) varies with different biosorbents as stated in Table 2. As the ionic radius of Ni(II) is comparatively low, it forms an octahedral structure combining with six H2O molecules when in contact with water, resulting in a large hydrated radius (Persson 2010). Therefore, more time is required to reach the equilibrium state of the biosorption process together with relatively low removal percentage.

Table 2 Optimum contact time for removal of Ni(II) for different biosorbents
Full size table

Thereafter, settling time was optimized for the most efficient removal for Ni(II) by the peel. According to the results, the extent of removal of Ni(II) was almost constant from the beginning with small fluctuations. Therefore, the optimum settling time was selected as 30 min at which 50% removal was obtained.

The effect of the initial solution pH on Ni(II) removal was studied at different pH values ranging from 1.0 to 7.0 at optimized shaking and settling times (Fig. 3). Solution pH, which affects the chemical composition and the surface charge of the biosorbent, is an important parameter in biosorption. According to Fig. 3, the extent of removal of Ni(II) is increased with an increase in pH up to 4. Low removal percentages of Ni(II) at low pH is probably due to the presence of high concentrations of H3O+, which can easily compete with hydrated Ni(II) for adsorption sites. Therefore, Ni(II) adsorption decreases due to repulsion of H3O+. Beyond pH 4, removal efficiency was almost constant up to pH 7.0. However, acidic pH of 5.9 is shown by aqueous suspensions of peel under ambient condition due to the carboxyl and hydroxyl groups present in the biosorbent.

Fig. 3
figure 3

Variation of extent of removal of Ni(II) at different pH (0.100 g peel, 10.0 mg L−1 of 50.0 mL solution, 120 min shaking time, 30 min settling time)

Full size image

Treatment temperature of 125 °C employed for processing the biosorbent would cause the removal of moisture, exposing pores for adsorption. A sufficient period of thermal treatment is thus important to effectively remove the moisture content. The effect of thermal treatment time on the extent of removal of Ni(II) shows the expected marginal increase (Fig. 4a). After 90 min of heating, no further increase in Ni(II) removal is observed, and thus, 90 min can be selected as the optimum thermal treatment period at a treatment temperature of 125 °C, at which 60% Ni(II) removal is observed.

Fig. 4
figure 4

Variation of extent of removal of Ni(II) with a thermal treatment time by biosorbent prepared at 125 °C and b treatment temperature of the biosorbent (0.100 g peel, 10.0 mg L−1 of 50.0 mL solution, 120 min shaking time, 30 min settling time, ambient pH of 5.9)

Full size image

Variation of the extent of Ni(II) removal at different treatment temperatures under the optimum conditions of thermal treatment time, shaking time and settling time is shown in Fig. 4b. According to Fig. 4b, the extent of removal of Ni(II) is generally increased with some fluctuations up to the treatment temperature of 175 °C, at which the maximum efficiency is recorded. The extent of removal is then sharply decreased, and hence, the optimum treatment temperature can be selected as 175 °C which leads to 71% removal.

Adsorption kinetics and equilibrium

The extent of heavy metal removal by peel of Artocarpus nobilis fruit at different contact times was investigated before the equilibrium was reached. These data were then used to check the validity of different kinetics models, as shown in Fig. 5. The amount of biosorption of Ni(II) at equilibrium (qe), determined from the pseudo-first-order model, is 2259 mg kg−1, which is in agreement with the experimental value of 2348 mg kg−1. Similar agreement has been reported in kinetics experiments of orange peel (Feng et al. 2011). Moreover, the regression coefficients of the pseudo-first-order and the pseudo-second-order models are 0.996 and 0.932, respectively, and therefore, the pseudo-first order is a better fit as compared to the pseudo-second-order model. However, a very low qe value of 55.55 mg kg−1 obtained for the pseudo-second-order model is much deviated from the experimental value. In addition, the rate constants of the pseudo-first-order and the pseudo-second-order models are 3.50 × 10−2 min−1 and 5.33 × 10−4 kg mg−1 min−1, respectively.

Fig. 5
figure 5

Plots of kinetics models for removal of Ni(II) from peel of Artocarpus nobilis fruit a Pseudo-first order, b Pseudo-second order [500.0 mL of 10.0 mg L−1 Ni(II) solution, 1.000 g of fruit peel]

Full size image

Biosorption data obtained within the concentration range of 10.0 and 1000 mg L−1 Ni(II) show a better fit with the linearized Langmuir isotherm model having a regression coefficient of 0.994 as compared to 0.927 obtained from the Freundlich isotherm model (Fig. 6), indicating the validity of the Langmuir model which shows a maximum adsorption capacity of 12,048 mg kg−1. In addition, the Langmuir isotherm constant (b), the Freundlich isotherm constant (kf) and the adsorption intensity (n) were calculated as 1.76 × 10−2 L mg−1, 1559 mg kg−1 and 3.26, respectively.

Fig. 6
figure 6

Adsorption isotherm for removal of Ni(II) by the peel of Artocarpus nobilis fruit. a Langmuir adsorption isotherm, b Freundlich adsorption isotherm

Full size image

Column experiments for removal of Ni(II)

Column experiments are generally conducted to determine the relationship between adsorbent and adsorbate by varying their amounts at equilibrium as a function of time. Metal ion removal by fixed bed columns can be used for prediction of characteristic breakthrough curves considering the mass transfer limitations revealed by mathematical models and the breakthrough curves representing a ratio of the effluent and influent metal ion concentrations as a function of time (Borba et al. 2006).

Optimization of flow rate

Breakthrough characteristics for the removal of Ni(II), monitored by investigating the relative concentration of Ni(II) in the eluent as a function of effluent volume (Veff) at a flow rate of 16.0 mL min−1, is shown in Fig. 7. Similar shapes for breakthrough curves were obtained for other flow rates ranging from 4.8 to 16.0 mL min−1 as well. The common feature to all breakthrough curves is that they show asymmetric profile, leveling off after a long time period.

Fig. 7
figure 7

Breakthrough curve of Ct/Co versus Veff of removal of Ni(II) with peel of Artocarpus nobilis fruit [Ni(II) concentration 10.0 mg L−1, flow rate 16.0 mL min−1, biosorbent mass 3.000 g, column height 10.0 cm, internal diameter of column 1.0 cm, sampling frequency 5 min]

Full size image

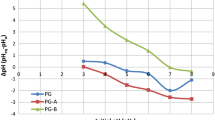
When the flow rates were increased from 4.8 to 16.0 mL min−1, removal percentages decreased as 97, 92, 93, 83 and 74%, respectively. Therefore, the flow rate of 8.4 mL min−1 was selected as the optimum by considering the maximum efficiency with less time consumption. The extent of removal of Ni(II) in each flow rate, applied to linearized dynamic adsorption models, namely Thomas, Adams–Bohart and Yoon–Nelson, is shown in Figure 8, and relevant constants are shown in Table 3.

Fig. 8
figure 8

Fitting of Ni(II) removal data for linearized dynamic adsorption models. a Thomas model, b Adams–Bohart model, c Yoon–Nelson model [Flow rate 16.0 mL min−1, bed height 10.0 cm, influent Ni(II) concentration 10.0 mg L−1]

Full size image
Table 3 Parameters determined from linearized dynamic models at different flow rates
Full size table

None of the models has shown a good agreement according to regression coefficients. However, the values of Thomas rate constant (Kth) increased with fluctuations from 1.142 to 1.262 mL mg−1 min−1, while equilibrium uptake per gram of the adsorbent (qo) was generally decreased from 5.46 to 3.92 mg g−1 with increasing flow rates. Biosorption of Congo red on rice husk, methylene blue on phoenix tree powder and phenol on activated sludge has shown that qo decreased while Thomas rate constants increased with increasing flow rates supporting the findings of this research (Han et al. 2009; Aksu and Gönen 2004). The rate constant (kAB) of the Adams–Bohart model decreases with increasing flow rates, and the saturation concentration (No) increases with increasing flow rates. The rate constant of the Yoon–Nelson model (kYN) slightly fluctuates and the time required for 50% adsorbate breakthrough (τ) decreases with increasing flow rates. The same phenomenon observed for both model and experimental parameters obtained for the time required for 50% adsorbate breakthrough. These parameters will be valuable in designing treatment systems for large-scale removal of Ni(II) from contaminated water or industrial effluents.

Optimization of bed height

Extent of removal investigated by passing Ni(II) solution of 10.0 mg L−1 through biosorbent-packed columns with different bed heights of 2.5, 5.0, 7.5 and 10.0 cm shows that removal percentages increase from 43 to 93% with an increase in bed height. The parameters obtained from different bed heights are shown in Table 4.

Table 4 Parameters of different dynamic models at different bed heights
Full size table

The rate constant (kAB) determined from the Adams–Bohart model increases while the saturation concentration (No) decreases with an increase in the bed height from 0.94 to 3.53 L mg−1 min−1. The rate constants determined from the Yoon–Nelson model (kYN) fluctuate between 1.02 × 10−2 and 1.21 × 10−2 min−1, and the τ values are similar to the experimental values of the model. In liquid–solid adsorption, adsorption process follows four basic steps: liquid-phase mass transfer, film diffusion, intra-particle mass transfer and adsorption–desorption reactions (Xu et al. 2013; Crittenden et al. 1986). During the adsorption/biosorption process, a film of the adsorbate creates on the surface of the adsorbent/biosorbent acting as an adsorption barrier for metal ions. Therefore, increase in the bed height would increase film thickness/resistance around the biosorbent. Consequently, sorption process decreases requiring more time to complete the biosorption process. However, the equilibrium uptake per gram of the adsorbent (qo) is increased while the saturation concentration (No) determined from the Adams–Bohart model is decreased.

According to Table 4, Thomas rate constant (Kth) decreases with an increase in bed height, while equilibrium uptake per gram of the adsorbent (qo) increases with an increase in bed height. The saturation concentration (No) decreases with an increase in bed height, while kAB increases with an increase in bed height. However, the rate constant of the Yoon–Nelson model (kYN) was not considerably changed.

Conclusion

Fruit peel of Artocarpus nobilis, a plant endemic to Sri Lanka, is proven to be an effective low-cost biosorbent for Ni(II). Carboxylic acid and its derivatives are the main functional groups present in the biosorbent as structural materials in cell walls to enhance the metal removal efficiency. Further, the negative charge of the biosorbent is an advantage for Ni(II) removal ability. Both these aspects contribute to a high adsorption capacity of 12,048 mg kg−1. Under static conditions, the maximum efficiency of Ni(II) removal reaches 71% at ambient pH level when experimental conditions are optimized. Further, removal efficiency of Ni(II) from synthetic solution is increased up to 93% under dynamic conditions at the optimum values of 10.0 cm for bed height and 8.4 mL min−1 for flow rate. Regression coefficients of dynamic model application show better agreement with the linearized relationship, demonstrating the validity of the results. These results suggest that the peel of Artocarpus nobilis is highly recommended for large-scale removal of Ni(II) from wastewater contaminated with Ni(II).